等腰三角形最值问题重难点突破2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 等腰三角形最值问题重难点突破2024-2025学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 09:47:19 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
等腰三角形最值问题重难点突破
最值(一) 斜大于垂
类型一 识别基本模型
1.如图,在平面直角坐标系中,A(5,0),B(0,m),连接AB,过点 A 作AC⊥AB,若AC=AB,M(-1,0),连接CM,当点B在y轴负半轴上移动时,CM 的最小值为 .
类型二 等线段代换
2.如图,∠MON=120°,A 为ON上一点,且,B 为直线OM上的一动点,以AB 为边作等边△ABC,连接OC.当 BC 最小时,此时OC 的长为 .
类型三 先算后求
3.如图,在等腰 Rt△ABC中,∠A=90°,AB=AC=6,DB=DC,点M,N分别在AB,AC 边上运动(点 M不与点A,B 重合),且∠MDN=90°,连接MN,则△AMN 的面积的最大值为 .
4.如图,在△ABC 中,BC=10,AC-AB=4,AD 是∠BAC 的角平分线,CD⊥AD,则 的最大值为( )
A.40 B.20 C.10 D.15
最值(二) 垂线段最短
类型一 错位全等找定角定线
1如图,在长方形ABCD 中, ,E 为边AB 上的点,且. 为AD 边上的动点,以 EF 为边在其右侧作等腰直角三角形GEF,EF=EG.设CD 的中点为 M,则MG 的最小值为 .
类型二 手拉手找定角定线
2.如图,等边△ABC 的边长为2,CD⊥AB 于点D,E 为射线CD上一点,以BE为边在 BE 左侧作等边△BEF,则DF 的最小值为( )
A.1 B.
3.如图,在等腰 中,∠ ,D为射线 AB 上一动点,以线段CD 为腰在右侧作等腰 且 ,连接AE,则AE 的最小值为( )
B.4 C.6 D.8
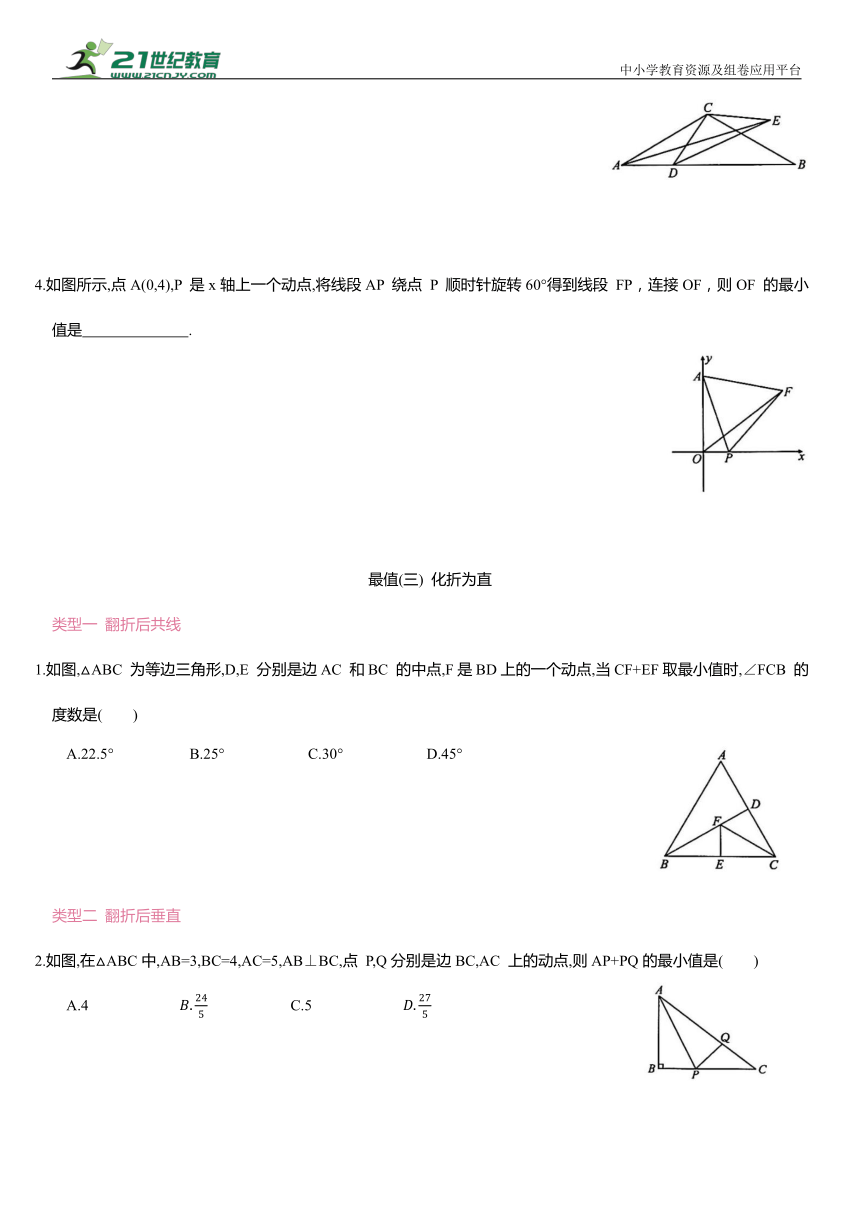
4.如图所示,点A(0,4),P 是x轴上一个动点,将线段AP 绕点 P 顺时针旋转60°得到线段 FP,连接OF,则OF 的最小值是 .
最值(三) 化折为直
类型一 翻折后共线
1.如图,△ABC 为等边三角形,D,E 分别是边AC 和BC 的中点,F是BD上的一个动点,当CF+EF取最小值时,∠FCB 的度数是( )
A.22.5° B.25° C.30° D.45°
类型二 翻折后垂直
2.如图,在△ABC中,AB=3,BC=4,AC=5,AB⊥BC,点 P,Q分别是边BC,AC 上的动点,则AP+PQ的最小值是( )
A.4 C.5
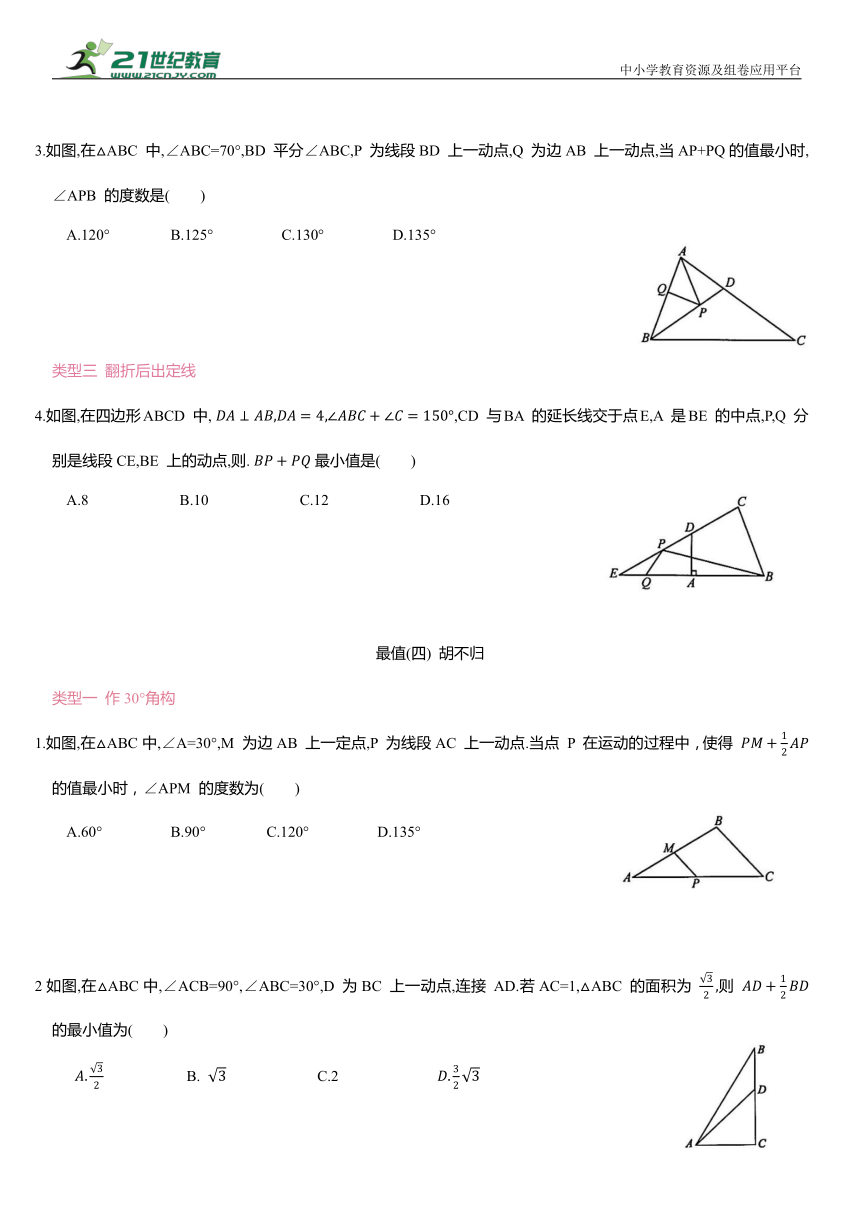
3.如图,在△ABC 中,∠ABC=70°,BD 平分∠ABC,P 为线段BD 上一动点,Q 为边AB 上一动点,当AP+PQ的值最小时,∠APB 的度数是( )
A.120° B.125° C.130° D.135°
类型三 翻折后出定线
4.如图,在四边形ABCD 中, ,CD 与BA 的延长线交于点E,A 是BE 的中点,P,Q 分别是线段CE,BE 上的动点,则. 最小值是( )
A.8 B.10 C.12 D.16
最值(四) 胡不归
类型一 作30°角构
1.如图,在△ABC中,∠A=30°,M 为边AB 上一定点,P 为线段AC 上一动点.当点 P 在运动的过程中,使得 的值最小时,∠APM 的度数为( )
A.60° B.90° C.120° D.135°
2如图,在△ABC中,∠ACB=90°,∠ABC=30°,D 为BC 上一动点,连接 AD.若AC=1,△ABC 的面积为 则 的最小值为( )
B. C.2
类型二 提系数构
3.如图,在△ABC 中,∠ACB=45°,点M 为边 BC 上的动点.当2AM+CM 最小时,∠CAM 的度数为( )
A.60° B.45° C.30° D.15°
4.如图,在长方形ABCD 中,BD=4,∠ABD=60°.将长方形 ABCD 沿 BD 折叠得到△BED,M是线段 BD上一动点.当BM+EM+CM的值最小时,DM 的长为( )
A.1 C.2 D.3
最值(五) 两点之间,线段最短
类型一 两定一变→基本型
1.如图,在 Rt△ABC 中,∠ACB=90°,AC=8,BC=6,D 为AB 上的一动点,将△BCD 沿CD 翻折得到△PCD,连接AP,当AP 取最小值时,△ACD 的面积是 .
类型二 等线段代换,定基本型
2如图,在△ADC 中,AD=2,CD=4,△ABC 与△ADE 均为等边三角形,连接BD.求 BD 的最大值.
类型三 构手拉手,定基本型
3.如图,在△ABC 中,AB=3,BC=5,△ACD 是等边三角形,连接 BD,当BD取最大值时,∠ABC 的度数为 .
4.如图,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4,O为BC的中点,OD=2,则当AC 取得最大值时,∠DCB 的度数为 .
最值(六)“将军饮马”
类型一 动点定直线
1.如图,等腰△ABC 的底边AB 的长为4,面积为12,BC 的垂直平分线MN 分别交BC,AC 于点M,N.若D 为AB 的中点,P 为线段MN 上一动点,则△PBD 的周长的最小值为 .
2.如图,在△ABC中,∠ACB=90°,D为AB 上一点,且3AD=2BD,P 为AC上一动点,当PD+PB 取最小值时,S△APB : S△BPC的值为 .
类型二 动点隐定直线
3.如图,BD 是等腰△ABC 的角平分线,AB=AC=6,BC=8,则 的值为 ;E 为线段BD(端点除外)上的一动点,连接AE,作∠EAF=∠BAC,且AE=AF,连接DF,则当△ADF 的周长最小时, 的值为 .
类型三 周长最值
4.如图,在四边形ABCD 中,∠C=70°,∠B=∠D=90°,E,F 分别是BC,DC上的点,当△AEF 的周长最小时,∠EAF 的度数为( )
A.30° B.40° C.50° D.70°
最值(七) 拼接最值
类型一 构错位全等拼接
1.如图,在等腰△ABC 中,∠BAC=100°,BD 是△ABC 的角平分线,N 为 BD 上一点,M为BC上一点,且BN=MC.当AM+AN的最小值为4时,AB 的长是 .
2.如图,CD 为△ABC 的高,其中∠CAB=58°,AC=AB,E,F 分别为线段CD,AC上的一动点,且AF=CE.当BF+AE 取最小值时,∠CFB 的度数为 .
类型二 构旋转全等拼接
3.如图,在等边△ABC中,M,N 分别为AB,BC 上的一动点,且BM=BN,D为AC上一定点,∠DBC=α.当DM+DN 最小时,直接写出∠DMB 的度数为 .(用含 a 的式子表示)
4.如图,AC=BC,∠ACB=90°. D,E,F 分别是边AB,AC,BC上的一点,且CE=CF,AD=2BD.当DE+DF 取最小值时, 的值为 .
最值(八) 费马点
类型一 构单手拉手
1.如图,在△ABC 中,AB=BC,∠ABC=70°,P 是△ABC 内一点,当 PA+PB+PC 的值最小时,∠PCA 的度数为 .
2.【阅读理解】已知等腰直角三角形的斜边长是直角边长的. 倍.
【变式运用】如图,在△ABC 中,AB=BC=3,∠ABC=30°,P 为△ABC 内一点,连接PA,PB,PC,则PA+PB+PC的最小值为 .
类型二 构双手拉手
3.如图,在等边△ABC 中,D 为直线AC 右侧一点,连接AD,BD,CD. O 为△ACD 内任意一点,BD=6,求OA+OC+OD 的最小值,并求取得这个最小值时∠AOC 的度数.
突破 42 最值(一) 斜大于垂
1.5 解:过点 C 作 CE⊥x 轴于点 E.则△CEA≌△AOB,
∴CE=OA=5,
∴点 C 在直线y=5上运动.
当 MC 与直线y=5 垂直时,CM 取最小值,最小值为5.
2. 解:过点 A 作 AE⊥OM 于点E, 以AE 为 边 作 等 边 三 角 形△AEF,连接OF.
∵∠MON=120°,△ABC 为等边三角形,
∴BC=AB,∠AOE=60°,
∴∠OAE=∠OAF,
∴△AOE≌△AOF,
∴OE=OF.
∵AB≥AE,
∴当点 B 与点E 重合时,
BC=AB最小,此时,点C 与点 F 重合,
3. 解:连接AD,过点 D作DE⊥AC于点E,则DE=AE=EC=3.
∵AD = BD,∠B=∠CAD = 45°,∠BDM=∠ADN,
∴△AND≌△BMD,
∴S四边形AMDN=S△ABD=9,
∴S△AMN = S四边形AMDN - S△MDN =
∵DN≥DE=3,
∴当 DN 取最小值3时,S△DMN 最小,此时 S△AMN 最大,
∴S△AMN的最大值为
4. C 解:延长AB,CD交于点E.
则△ADE≌△ADC,
∴ED=DC,AE=AC,
∴BE=AE--AB=AC-AB=4.
过点 C 作CH⊥AB 于点 H,S△BDC CH≤BC=10.
当点 H 与点 B 重合,即∠ABC=90°时,S△BDC 取最大值10,选 C.
突破 43 最值(二) 垂线段最短
1.2 解:过点 G 作GH⊥AB 于点 H,过点 G 作 PN∥AB,
∴∠EHG=90°,
AD=BC=3,
∴∠AFE+∠FEA=90°.
∵△GEF 是等腰直角三角形,EF=EG,
∴∠FEG=90°,
∴∠HEG+∠FEA=90°,
∴∠HEG=∠AFE,
∴△GEH≌△EFA,
∴GH=EA=1,
∴点G 在平行于AB 且到 AB 距离为 1 的直线 PN 上运动.
当 M,G,H 三点共线时,MH⊥AB,则MH⊥PN,此时MG 有最小值,
此时 MG 的最小值为MH-GH=3-1=2.
2. B 解:连接AF.
∵△ABC,△EFB 为等边三角形,
∴∠ABC=∠ACB=∠EBF=60°,AB=BC,EB=FB,
∴∠ABF=∠CBE,
∴△ABF≌△CBE,
∴∠FAB=∠ECB.
∵CA=CB,CD⊥AB,
∴∠FAB=30°,
∴当∠DFA=90°时,DF 取最小值,最小值为 故选 B.
3. C 解:连接 BE 并延长,交 AC 的延长线于点 H.
∴∠ACD=∠BCE.
∵AC=BC,CD=CE,
∴△ACD≌△BCE,
∴∠CAD=∠CBE=30°,∠ABE=60°,
∴点 E 的运动路径是直线AB 的上方,且使得∠ABE=60°的射线上.
∵∠BAH=30°,
∵AE≥AH,
∵AH=AC+CH=4+2=6,
∴AE≥6,AE 的最小值为 6.
故选 C.
4.2 解:以 AO 为边作等边△AOC,连接 FC,
由题意,得△APF 为等边三角形,
∴AO=AC=4,∠OAC=60°,
∠PAF=60°,AP=AF,
易证△AOP≌△ACF,
∴∠ACF=∠AOP=90°,即 FC⊥AC,
∴点 F 在直线 FC 上运动.
过点 O 作OF'⊥FC 交直线 FC 于点 F',
∴OF≥OF'.
∵∠ACO=60°,AO=OC=4,
∴当点 F 在直线 FC 上运动到点 F'位置时,线段 OF 的最小值为
突破 44 最值(三) 化折为直
1. C 解:连接AF,则AF=CF,
∴CF+EF=AF+EF≥AE.
当A,F,E 三点共线时,CF+EF 取最小值,∠FCB=30°.选 C.
2. B 解:作点 A 关于 BC 的对称点M,过点 M 作 MN⊥AC 于点 N,连接 MP,MC,
∴AP+PQ=MP+PQ≥MN,
∴AP+PQ的最小值为MN,
故选 B.
3. B 解:在 BC 上截取BE=BQ,连接PE,AE.
可得△BPE≌△BPQ,
∴PE=PQ.
过点 A 作 AH⊥BC 于点 H,则 AP+PQ=AP+PE≥AE≥AH.
当点 A,P,H 三点共线时,AP +PQ取最小值,
此时∠APB=∠PBC+∠AHB= 选 B.
4. C 解:将EB 沿EC 翻折,得到 EF,∠FEC=∠CEB =180°—(∠ABC+∠C)=30°.
在 EF 上取点M,使 EM=EQ,连接PM,连接BD 并延长交EF 于点N.
由△EPQ≌△EPM,得 PM=PQ.
∵DA⊥BE,AE=AB,
∴DB=DE=2AD=8,
∴∠DBE=∠DEB=30°,
∴∠NEB+∠NBE=90°,
∴∠ENB=90°,
∴PB+PQ=PB+PM≥BM≥BN= 选 C.
突破 45 最值(四) 胡不归
1. C 解:在 AC 下方作∠CAT =∠CAB=30°,过点 P 作 PE⊥AT于点E,过点 M 作 MF⊥AT 于点F,交 AC 于点G.
∵∠AEP=90°,∠PAE=30°,
∴MP+PE≥MF,
∴当点 P 与G 重合时,点 E 与F 重合, 的值最小,此时∠APM = ∠AGM = ∠CAT +∠MFA=120°.故选 C.
2. B 解:作点 A 关于BC 的对称点F,连接CF,则△ABF 为等边三角形,作 DH⊥BF 于点 H,
则
∴当AH⊥BF 时,AH 最小.
∵∠ABC=30°,AC=1,
的最小值为 .故选B.
3. D 解:在 BC下方作∠BCN=30°,过点 M 作ME⊥CN 于点E,过点 A作 AF⊥CN 于点F,
则ME = CM,2AM + CM = 2AF.
当点 M 在AF 上时,2AM+CM 取最小值,
此时2 .故选 D.
4. C 解:过点 M 作MF⊥BC 于点F,作 EH⊥BC 于点 H,连接 EC.
BM+EM+CM = BM +2EM = 2EH,当E,M,F 三点共线,即点 F与点H 重合时,BM+EM+CM取最小值.
∵△EBC 为等边三角形,EH⊥BC,
∴H 为BC 的中点,此时BM=MC,
∴∠MCB=∠MBC=30°,可得△MCD 为等边三角形,
∴MD=MC,
∴BM=MC=MD,
故选 C.
突破 46 最值(五)两点之间,线段最短
1. 解:∵AP≥AC-CP,当点 P落在AC上时,AP 最小,此时CD平分∠ACB.
过点 D 作 DG⊥AC 于点 G,作 DF⊥BC于点 F,∠ACD=∠BCD,PC=BC=6,
∴DG=DF,
2.解:连接EC.
∵∠BAC=∠EAD=60°,
∴∠DAB=∠EAC.
∵EA=DA,AB=AC,
∴△EAC≌△DAB,
∴EC=DB.
在△EDC中,ED=AD=2,DC=4,EC≤DE+DC=2+4=6.
当E,D,C 三点共线时,EC 取最大值 6,
∴BD 的最大值为6.
3.120° 解:以 AB 为边在△ABC 外作等边△ABE,连接 CE,则 AB =BE=AE.
∵△ACD是等边三角形,
∴AD=AC,∠DAC=60°.
∵∠BAE=60°,
∴ ∠DAC + ∠BAC = ∠BAE +∠BAC,即∠EAC=∠BAD,
∴△EAC≌△BAD(SAS),
∴EC=BD.
∵BC+BE≥CE,
∴当 E 在 CB 的延长线上时,CE 取得最大值为EB+BC=AB+BC=3+5=8,
∴BD 的最大值为 8.此时,∠ABC
4.45° 解:在 BC下方作等边△BCM,连接OM,DM,则△DBM≌△ABC,
∴AC=DM≤OD+OM.
∵OD,OM 均为定长,
∴当D,O,M 三点共线时,DM 取最大值.
∵OM⊥BC,
∴∠DOC=90°,
∴∠DCB=45°.
突破47 最值(六)“将军饮马”
1.8 解:连接CD,CP.
∵CA=CB,D 是AB 边的中点,
∴CD⊥AB,
∴CD=6.
∵MN 垂直平分 BC,
∴PB=PC,
∴PB+PD+BD=PB+PD+2=2+CP+DP≥2+CD=8,
∴当点 P 在CD 上时,△PBD 的周长取最小值为8.
2. 解:作点B 关于AC 的对称点B',连接 B'D,B'A,B'D 交AC 于点P'.
当点 P 位于点 P'时,PD+PB 取最小值B'D.
设 3S△APD=2x,S△PBC=y,
则S△BPD=3x,S△B'AD=7x,
∴7x:(2y+3x)=2:3,
∴15x=4y,
∴此时S△APB : S△BPC =5x : y=
3. 解:∵BD 平分∠ABC,∴点 D 到 BA,BC 的距离相等,其距离设为h,
连接CF,易证△ABE≌△ACF,∴∠ABE=∠ACF 为定角.
作点 A 关于直线CF 的对称点 A',
∴A'F=AF.
∵AD 为定长,
∴△ADF 的周长为AD+AF+DF
∴当A',F,D 三点共线时,△ADF的周长取最小值,此时
4. B 解:分别作点 A 关于 BC 和CD的对称点 A',A",连接 A'A",交 BC于点E,交 CD 于点 F,则A'A'即为△AEF 的周长最小值.此时A',F,E,A"四点共线.
∵∠C=70°,.
∴∠DAB=110°,
∴∠A'+∠A'=70°.
∵∠A'=∠EAA',∠FAD=∠A",
∴∠EAA'+∠A"AF=70°,
∴∠EAF=110°-70°=40°.故选 B.
突破 48 最值(七) 拼接最值
1.4 解:可得∠ABD=20°,在CB下方作∠A'CB=∠ABD =20°,且使A'C=AC,
则 AB=A'C,∠ACA'=∠ACB+∠A'CB=60°,
∴△AA'C是等边三角形.
∵BN = CM,∠ABN =∠A'CM,AB=A'C,
∴△ABN≌△A'CM,
∴AN=A'M,
∴AM+AN=AM+A'M≥AA',
∴当A,M,A'在同一直线上时,AM+AN 最小,最小值为AA'=4,
2.103° 解:过点 A 向上作AH⊥AB,且使AH=AC,
连 接 BH, FH, 可 证 △AEC ≌△HFA,
∴AE=HF,
∴BF+AE=BF+HF,
∴当 F 为 AC 与 BH 的交点时,BF+AE的值最小,
此时∠FBA=45°,∠CAB=58°,
∴∠CFB = ∠FBA + ∠CAB =103°.
3.60°+α 解:在BD 下 方 作等边△BDH,连接 NH.
易证△BMD≌△BNH,
∴DM=NH,
∴DM+DN=NH+DN,
∴当D,N,H 共线时,DM+DN 取最小值DH=BD,
此时∠DMB=∠BNH=∠DBC+∠BDH=60°+α.
4.2 解:连接 CD,将△ACD 绕点 C逆时针旋转 90°得到△BCG,连接FG,DG,
则∠CBG=∠A=∠ABC=45°,BG=AD=2DB.
可证△CGF≌△CDE,
∴GF=DE,
∴DE+DF=GF+DF≥GD,
∴当G,F,D三点共线时,DE+DF取最小值,
此时
突破 49 最值(八) 费马点
1.30° 解:将△ABP 绕点 B 逆时针旋转 60°得到△EBD,连接 DP,EC.
则△BPD 为等边三角形,
∴BP=DP,
∴PA+PB+PC=ED+DP+PC≥EC.
当点 E,D,P,C 四点共线时,PA+PB+PC取最小值,
此时∠ECA =∠PCA =∠BCA -∠BCE.
∵BE=BC,
∠EBC=60°+70°=130°,
∴∠BCE=∠BEC=25°.
∵BA=BC,
∴∠BCA=∠BAC=55°,
2.3 解:将△ABP 绕点 B 逆时针旋转60°得到△EBF,连接 PF,EC,
∴AB=BE=3,BP=BF,
∴△PBF 是等边三角形,
∴PB=PF.
∵PA=EF,
∴PA+PB+PC=PC+PF+EF.
∵PC+PF+EF≥EC,
∴当点 P,F 在直线 EC 上时,PA+PB+PC的值最小.
∵∠CBE=∠ABC+∠ABE=90°,BE=BC,
∴△EBC 为等腰直角三角形,
∴PA+PB+PC的最小值为3
3.解:在 AO 上方作等边△AON,作∠HAD = 60°, AH = AD, 连 接NH,CH,
则△AOD≌△ANH,
∴NH=OD,
∴OA+OC+OD=ON+OC+NH≥CH.
当H,N,O,C 共线时,OA+OC+OD 取最小值CH,可证△ABD≌△ACH,
∴CH=BD=6,
∴OA+OC+OD 的最小值为6,此时 ∠AOC = 180°- ∠AON =120°.
等腰三角形最值问题重难点突破
最值(一) 斜大于垂
类型一 识别基本模型
1.如图,在平面直角坐标系中,A(5,0),B(0,m),连接AB,过点 A 作AC⊥AB,若AC=AB,M(-1,0),连接CM,当点B在y轴负半轴上移动时,CM 的最小值为 .
类型二 等线段代换
2.如图,∠MON=120°,A 为ON上一点,且,B 为直线OM上的一动点,以AB 为边作等边△ABC,连接OC.当 BC 最小时,此时OC 的长为 .
类型三 先算后求
3.如图,在等腰 Rt△ABC中,∠A=90°,AB=AC=6,DB=DC,点M,N分别在AB,AC 边上运动(点 M不与点A,B 重合),且∠MDN=90°,连接MN,则△AMN 的面积的最大值为 .
4.如图,在△ABC 中,BC=10,AC-AB=4,AD 是∠BAC 的角平分线,CD⊥AD,则 的最大值为( )
A.40 B.20 C.10 D.15
最值(二) 垂线段最短
类型一 错位全等找定角定线
1如图,在长方形ABCD 中, ,E 为边AB 上的点,且. 为AD 边上的动点,以 EF 为边在其右侧作等腰直角三角形GEF,EF=EG.设CD 的中点为 M,则MG 的最小值为 .
类型二 手拉手找定角定线
2.如图,等边△ABC 的边长为2,CD⊥AB 于点D,E 为射线CD上一点,以BE为边在 BE 左侧作等边△BEF,则DF 的最小值为( )
A.1 B.
3.如图,在等腰 中,∠ ,D为射线 AB 上一动点,以线段CD 为腰在右侧作等腰 且 ,连接AE,则AE 的最小值为( )
B.4 C.6 D.8
4.如图所示,点A(0,4),P 是x轴上一个动点,将线段AP 绕点 P 顺时针旋转60°得到线段 FP,连接OF,则OF 的最小值是 .
最值(三) 化折为直
类型一 翻折后共线
1.如图,△ABC 为等边三角形,D,E 分别是边AC 和BC 的中点,F是BD上的一个动点,当CF+EF取最小值时,∠FCB 的度数是( )
A.22.5° B.25° C.30° D.45°
类型二 翻折后垂直
2.如图,在△ABC中,AB=3,BC=4,AC=5,AB⊥BC,点 P,Q分别是边BC,AC 上的动点,则AP+PQ的最小值是( )
A.4 C.5
3.如图,在△ABC 中,∠ABC=70°,BD 平分∠ABC,P 为线段BD 上一动点,Q 为边AB 上一动点,当AP+PQ的值最小时,∠APB 的度数是( )
A.120° B.125° C.130° D.135°
类型三 翻折后出定线
4.如图,在四边形ABCD 中, ,CD 与BA 的延长线交于点E,A 是BE 的中点,P,Q 分别是线段CE,BE 上的动点,则. 最小值是( )
A.8 B.10 C.12 D.16
最值(四) 胡不归
类型一 作30°角构
1.如图,在△ABC中,∠A=30°,M 为边AB 上一定点,P 为线段AC 上一动点.当点 P 在运动的过程中,使得 的值最小时,∠APM 的度数为( )
A.60° B.90° C.120° D.135°
2如图,在△ABC中,∠ACB=90°,∠ABC=30°,D 为BC 上一动点,连接 AD.若AC=1,△ABC 的面积为 则 的最小值为( )
B. C.2
类型二 提系数构
3.如图,在△ABC 中,∠ACB=45°,点M 为边 BC 上的动点.当2AM+CM 最小时,∠CAM 的度数为( )
A.60° B.45° C.30° D.15°
4.如图,在长方形ABCD 中,BD=4,∠ABD=60°.将长方形 ABCD 沿 BD 折叠得到△BED,M是线段 BD上一动点.当BM+EM+CM的值最小时,DM 的长为( )
A.1 C.2 D.3
最值(五) 两点之间,线段最短
类型一 两定一变→基本型
1.如图,在 Rt△ABC 中,∠ACB=90°,AC=8,BC=6,D 为AB 上的一动点,将△BCD 沿CD 翻折得到△PCD,连接AP,当AP 取最小值时,△ACD 的面积是 .
类型二 等线段代换,定基本型
2如图,在△ADC 中,AD=2,CD=4,△ABC 与△ADE 均为等边三角形,连接BD.求 BD 的最大值.
类型三 构手拉手,定基本型
3.如图,在△ABC 中,AB=3,BC=5,△ACD 是等边三角形,连接 BD,当BD取最大值时,∠ABC 的度数为 .
4.如图,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4,O为BC的中点,OD=2,则当AC 取得最大值时,∠DCB 的度数为 .
最值(六)“将军饮马”
类型一 动点定直线
1.如图,等腰△ABC 的底边AB 的长为4,面积为12,BC 的垂直平分线MN 分别交BC,AC 于点M,N.若D 为AB 的中点,P 为线段MN 上一动点,则△PBD 的周长的最小值为 .
2.如图,在△ABC中,∠ACB=90°,D为AB 上一点,且3AD=2BD,P 为AC上一动点,当PD+PB 取最小值时,S△APB : S△BPC的值为 .
类型二 动点隐定直线
3.如图,BD 是等腰△ABC 的角平分线,AB=AC=6,BC=8,则 的值为 ;E 为线段BD(端点除外)上的一动点,连接AE,作∠EAF=∠BAC,且AE=AF,连接DF,则当△ADF 的周长最小时, 的值为 .
类型三 周长最值
4.如图,在四边形ABCD 中,∠C=70°,∠B=∠D=90°,E,F 分别是BC,DC上的点,当△AEF 的周长最小时,∠EAF 的度数为( )
A.30° B.40° C.50° D.70°
最值(七) 拼接最值
类型一 构错位全等拼接
1.如图,在等腰△ABC 中,∠BAC=100°,BD 是△ABC 的角平分线,N 为 BD 上一点,M为BC上一点,且BN=MC.当AM+AN的最小值为4时,AB 的长是 .
2.如图,CD 为△ABC 的高,其中∠CAB=58°,AC=AB,E,F 分别为线段CD,AC上的一动点,且AF=CE.当BF+AE 取最小值时,∠CFB 的度数为 .
类型二 构旋转全等拼接
3.如图,在等边△ABC中,M,N 分别为AB,BC 上的一动点,且BM=BN,D为AC上一定点,∠DBC=α.当DM+DN 最小时,直接写出∠DMB 的度数为 .(用含 a 的式子表示)
4.如图,AC=BC,∠ACB=90°. D,E,F 分别是边AB,AC,BC上的一点,且CE=CF,AD=2BD.当DE+DF 取最小值时, 的值为 .
最值(八) 费马点
类型一 构单手拉手
1.如图,在△ABC 中,AB=BC,∠ABC=70°,P 是△ABC 内一点,当 PA+PB+PC 的值最小时,∠PCA 的度数为 .
2.【阅读理解】已知等腰直角三角形的斜边长是直角边长的. 倍.
【变式运用】如图,在△ABC 中,AB=BC=3,∠ABC=30°,P 为△ABC 内一点,连接PA,PB,PC,则PA+PB+PC的最小值为 .
类型二 构双手拉手
3.如图,在等边△ABC 中,D 为直线AC 右侧一点,连接AD,BD,CD. O 为△ACD 内任意一点,BD=6,求OA+OC+OD 的最小值,并求取得这个最小值时∠AOC 的度数.
突破 42 最值(一) 斜大于垂
1.5 解:过点 C 作 CE⊥x 轴于点 E.则△CEA≌△AOB,
∴CE=OA=5,
∴点 C 在直线y=5上运动.
当 MC 与直线y=5 垂直时,CM 取最小值,最小值为5.
2. 解:过点 A 作 AE⊥OM 于点E, 以AE 为 边 作 等 边 三 角 形△AEF,连接OF.
∵∠MON=120°,△ABC 为等边三角形,
∴BC=AB,∠AOE=60°,
∴∠OAE=∠OAF,
∴△AOE≌△AOF,
∴OE=OF.
∵AB≥AE,
∴当点 B 与点E 重合时,
BC=AB最小,此时,点C 与点 F 重合,
3. 解:连接AD,过点 D作DE⊥AC于点E,则DE=AE=EC=3.
∵AD = BD,∠B=∠CAD = 45°,∠BDM=∠ADN,
∴△AND≌△BMD,
∴S四边形AMDN=S△ABD=9,
∴S△AMN = S四边形AMDN - S△MDN =
∵DN≥DE=3,
∴当 DN 取最小值3时,S△DMN 最小,此时 S△AMN 最大,
∴S△AMN的最大值为
4. C 解:延长AB,CD交于点E.
则△ADE≌△ADC,
∴ED=DC,AE=AC,
∴BE=AE--AB=AC-AB=4.
过点 C 作CH⊥AB 于点 H,S△BDC CH≤BC=10.
当点 H 与点 B 重合,即∠ABC=90°时,S△BDC 取最大值10,选 C.
突破 43 最值(二) 垂线段最短
1.2 解:过点 G 作GH⊥AB 于点 H,过点 G 作 PN∥AB,
∴∠EHG=90°,
AD=BC=3,
∴∠AFE+∠FEA=90°.
∵△GEF 是等腰直角三角形,EF=EG,
∴∠FEG=90°,
∴∠HEG+∠FEA=90°,
∴∠HEG=∠AFE,
∴△GEH≌△EFA,
∴GH=EA=1,
∴点G 在平行于AB 且到 AB 距离为 1 的直线 PN 上运动.
当 M,G,H 三点共线时,MH⊥AB,则MH⊥PN,此时MG 有最小值,
此时 MG 的最小值为MH-GH=3-1=2.
2. B 解:连接AF.
∵△ABC,△EFB 为等边三角形,
∴∠ABC=∠ACB=∠EBF=60°,AB=BC,EB=FB,
∴∠ABF=∠CBE,
∴△ABF≌△CBE,
∴∠FAB=∠ECB.
∵CA=CB,CD⊥AB,
∴∠FAB=30°,
∴当∠DFA=90°时,DF 取最小值,最小值为 故选 B.
3. C 解:连接 BE 并延长,交 AC 的延长线于点 H.
∴∠ACD=∠BCE.
∵AC=BC,CD=CE,
∴△ACD≌△BCE,
∴∠CAD=∠CBE=30°,∠ABE=60°,
∴点 E 的运动路径是直线AB 的上方,且使得∠ABE=60°的射线上.
∵∠BAH=30°,
∵AE≥AH,
∵AH=AC+CH=4+2=6,
∴AE≥6,AE 的最小值为 6.
故选 C.
4.2 解:以 AO 为边作等边△AOC,连接 FC,
由题意,得△APF 为等边三角形,
∴AO=AC=4,∠OAC=60°,
∠PAF=60°,AP=AF,
易证△AOP≌△ACF,
∴∠ACF=∠AOP=90°,即 FC⊥AC,
∴点 F 在直线 FC 上运动.
过点 O 作OF'⊥FC 交直线 FC 于点 F',
∴OF≥OF'.
∵∠ACO=60°,AO=OC=4,
∴当点 F 在直线 FC 上运动到点 F'位置时,线段 OF 的最小值为
突破 44 最值(三) 化折为直
1. C 解:连接AF,则AF=CF,
∴CF+EF=AF+EF≥AE.
当A,F,E 三点共线时,CF+EF 取最小值,∠FCB=30°.选 C.
2. B 解:作点 A 关于 BC 的对称点M,过点 M 作 MN⊥AC 于点 N,连接 MP,MC,
∴AP+PQ=MP+PQ≥MN,
∴AP+PQ的最小值为MN,
故选 B.
3. B 解:在 BC 上截取BE=BQ,连接PE,AE.
可得△BPE≌△BPQ,
∴PE=PQ.
过点 A 作 AH⊥BC 于点 H,则 AP+PQ=AP+PE≥AE≥AH.
当点 A,P,H 三点共线时,AP +PQ取最小值,
此时∠APB=∠PBC+∠AHB= 选 B.
4. C 解:将EB 沿EC 翻折,得到 EF,∠FEC=∠CEB =180°—(∠ABC+∠C)=30°.
在 EF 上取点M,使 EM=EQ,连接PM,连接BD 并延长交EF 于点N.
由△EPQ≌△EPM,得 PM=PQ.
∵DA⊥BE,AE=AB,
∴DB=DE=2AD=8,
∴∠DBE=∠DEB=30°,
∴∠NEB+∠NBE=90°,
∴∠ENB=90°,
∴PB+PQ=PB+PM≥BM≥BN= 选 C.
突破 45 最值(四) 胡不归
1. C 解:在 AC 下方作∠CAT =∠CAB=30°,过点 P 作 PE⊥AT于点E,过点 M 作 MF⊥AT 于点F,交 AC 于点G.
∵∠AEP=90°,∠PAE=30°,
∴MP+PE≥MF,
∴当点 P 与G 重合时,点 E 与F 重合, 的值最小,此时∠APM = ∠AGM = ∠CAT +∠MFA=120°.故选 C.
2. B 解:作点 A 关于BC 的对称点F,连接CF,则△ABF 为等边三角形,作 DH⊥BF 于点 H,
则
∴当AH⊥BF 时,AH 最小.
∵∠ABC=30°,AC=1,
的最小值为 .故选B.
3. D 解:在 BC下方作∠BCN=30°,过点 M 作ME⊥CN 于点E,过点 A作 AF⊥CN 于点F,
则ME = CM,2AM + CM = 2AF.
当点 M 在AF 上时,2AM+CM 取最小值,
此时2 .故选 D.
4. C 解:过点 M 作MF⊥BC 于点F,作 EH⊥BC 于点 H,连接 EC.
BM+EM+CM = BM +2EM = 2EH,当E,M,F 三点共线,即点 F与点H 重合时,BM+EM+CM取最小值.
∵△EBC 为等边三角形,EH⊥BC,
∴H 为BC 的中点,此时BM=MC,
∴∠MCB=∠MBC=30°,可得△MCD 为等边三角形,
∴MD=MC,
∴BM=MC=MD,
故选 C.
突破 46 最值(五)两点之间,线段最短
1. 解:∵AP≥AC-CP,当点 P落在AC上时,AP 最小,此时CD平分∠ACB.
过点 D 作 DG⊥AC 于点 G,作 DF⊥BC于点 F,∠ACD=∠BCD,PC=BC=6,
∴DG=DF,
2.解:连接EC.
∵∠BAC=∠EAD=60°,
∴∠DAB=∠EAC.
∵EA=DA,AB=AC,
∴△EAC≌△DAB,
∴EC=DB.
在△EDC中,ED=AD=2,DC=4,EC≤DE+DC=2+4=6.
当E,D,C 三点共线时,EC 取最大值 6,
∴BD 的最大值为6.
3.120° 解:以 AB 为边在△ABC 外作等边△ABE,连接 CE,则 AB =BE=AE.
∵△ACD是等边三角形,
∴AD=AC,∠DAC=60°.
∵∠BAE=60°,
∴ ∠DAC + ∠BAC = ∠BAE +∠BAC,即∠EAC=∠BAD,
∴△EAC≌△BAD(SAS),
∴EC=BD.
∵BC+BE≥CE,
∴当 E 在 CB 的延长线上时,CE 取得最大值为EB+BC=AB+BC=3+5=8,
∴BD 的最大值为 8.此时,∠ABC
4.45° 解:在 BC下方作等边△BCM,连接OM,DM,则△DBM≌△ABC,
∴AC=DM≤OD+OM.
∵OD,OM 均为定长,
∴当D,O,M 三点共线时,DM 取最大值.
∵OM⊥BC,
∴∠DOC=90°,
∴∠DCB=45°.
突破47 最值(六)“将军饮马”
1.8 解:连接CD,CP.
∵CA=CB,D 是AB 边的中点,
∴CD⊥AB,
∴CD=6.
∵MN 垂直平分 BC,
∴PB=PC,
∴PB+PD+BD=PB+PD+2=2+CP+DP≥2+CD=8,
∴当点 P 在CD 上时,△PBD 的周长取最小值为8.
2. 解:作点B 关于AC 的对称点B',连接 B'D,B'A,B'D 交AC 于点P'.
当点 P 位于点 P'时,PD+PB 取最小值B'D.
设 3S△APD=2x,S△PBC=y,
则S△BPD=3x,S△B'AD=7x,
∴7x:(2y+3x)=2:3,
∴15x=4y,
∴此时S△APB : S△BPC =5x : y=
3. 解:∵BD 平分∠ABC,∴点 D 到 BA,BC 的距离相等,其距离设为h,
连接CF,易证△ABE≌△ACF,∴∠ABE=∠ACF 为定角.
作点 A 关于直线CF 的对称点 A',
∴A'F=AF.
∵AD 为定长,
∴△ADF 的周长为AD+AF+DF
∴当A',F,D 三点共线时,△ADF的周长取最小值,此时
4. B 解:分别作点 A 关于 BC 和CD的对称点 A',A",连接 A'A",交 BC于点E,交 CD 于点 F,则A'A'即为△AEF 的周长最小值.此时A',F,E,A"四点共线.
∵∠C=70°,.
∴∠DAB=110°,
∴∠A'+∠A'=70°.
∵∠A'=∠EAA',∠FAD=∠A",
∴∠EAA'+∠A"AF=70°,
∴∠EAF=110°-70°=40°.故选 B.
突破 48 最值(七) 拼接最值
1.4 解:可得∠ABD=20°,在CB下方作∠A'CB=∠ABD =20°,且使A'C=AC,
则 AB=A'C,∠ACA'=∠ACB+∠A'CB=60°,
∴△AA'C是等边三角形.
∵BN = CM,∠ABN =∠A'CM,AB=A'C,
∴△ABN≌△A'CM,
∴AN=A'M,
∴AM+AN=AM+A'M≥AA',
∴当A,M,A'在同一直线上时,AM+AN 最小,最小值为AA'=4,
2.103° 解:过点 A 向上作AH⊥AB,且使AH=AC,
连 接 BH, FH, 可 证 △AEC ≌△HFA,
∴AE=HF,
∴BF+AE=BF+HF,
∴当 F 为 AC 与 BH 的交点时,BF+AE的值最小,
此时∠FBA=45°,∠CAB=58°,
∴∠CFB = ∠FBA + ∠CAB =103°.
3.60°+α 解:在BD 下 方 作等边△BDH,连接 NH.
易证△BMD≌△BNH,
∴DM=NH,
∴DM+DN=NH+DN,
∴当D,N,H 共线时,DM+DN 取最小值DH=BD,
此时∠DMB=∠BNH=∠DBC+∠BDH=60°+α.
4.2 解:连接 CD,将△ACD 绕点 C逆时针旋转 90°得到△BCG,连接FG,DG,
则∠CBG=∠A=∠ABC=45°,BG=AD=2DB.
可证△CGF≌△CDE,
∴GF=DE,
∴DE+DF=GF+DF≥GD,
∴当G,F,D三点共线时,DE+DF取最小值,
此时
突破 49 最值(八) 费马点
1.30° 解:将△ABP 绕点 B 逆时针旋转 60°得到△EBD,连接 DP,EC.
则△BPD 为等边三角形,
∴BP=DP,
∴PA+PB+PC=ED+DP+PC≥EC.
当点 E,D,P,C 四点共线时,PA+PB+PC取最小值,
此时∠ECA =∠PCA =∠BCA -∠BCE.
∵BE=BC,
∠EBC=60°+70°=130°,
∴∠BCE=∠BEC=25°.
∵BA=BC,
∴∠BCA=∠BAC=55°,
2.3 解:将△ABP 绕点 B 逆时针旋转60°得到△EBF,连接 PF,EC,
∴AB=BE=3,BP=BF,
∴△PBF 是等边三角形,
∴PB=PF.
∵PA=EF,
∴PA+PB+PC=PC+PF+EF.
∵PC+PF+EF≥EC,
∴当点 P,F 在直线 EC 上时,PA+PB+PC的值最小.
∵∠CBE=∠ABC+∠ABE=90°,BE=BC,
∴△EBC 为等腰直角三角形,
∴PA+PB+PC的最小值为3
3.解:在 AO 上方作等边△AON,作∠HAD = 60°, AH = AD, 连 接NH,CH,
则△AOD≌△ANH,
∴NH=OD,
∴OA+OC+OD=ON+OC+NH≥CH.
当H,N,O,C 共线时,OA+OC+OD 取最小值CH,可证△ABD≌△ACH,
∴CH=BD=6,
∴OA+OC+OD 的最小值为6,此时 ∠AOC = 180°- ∠AON =120°.
