求角思想方法专项突破(含解析)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 求角思想方法专项突破(含解析)2024-2025学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 09:49:43 | ||
图片预览

文档简介
求角思想方法专项突破
突破11 求角思想方法(一) 方程思想
类型一 设一元
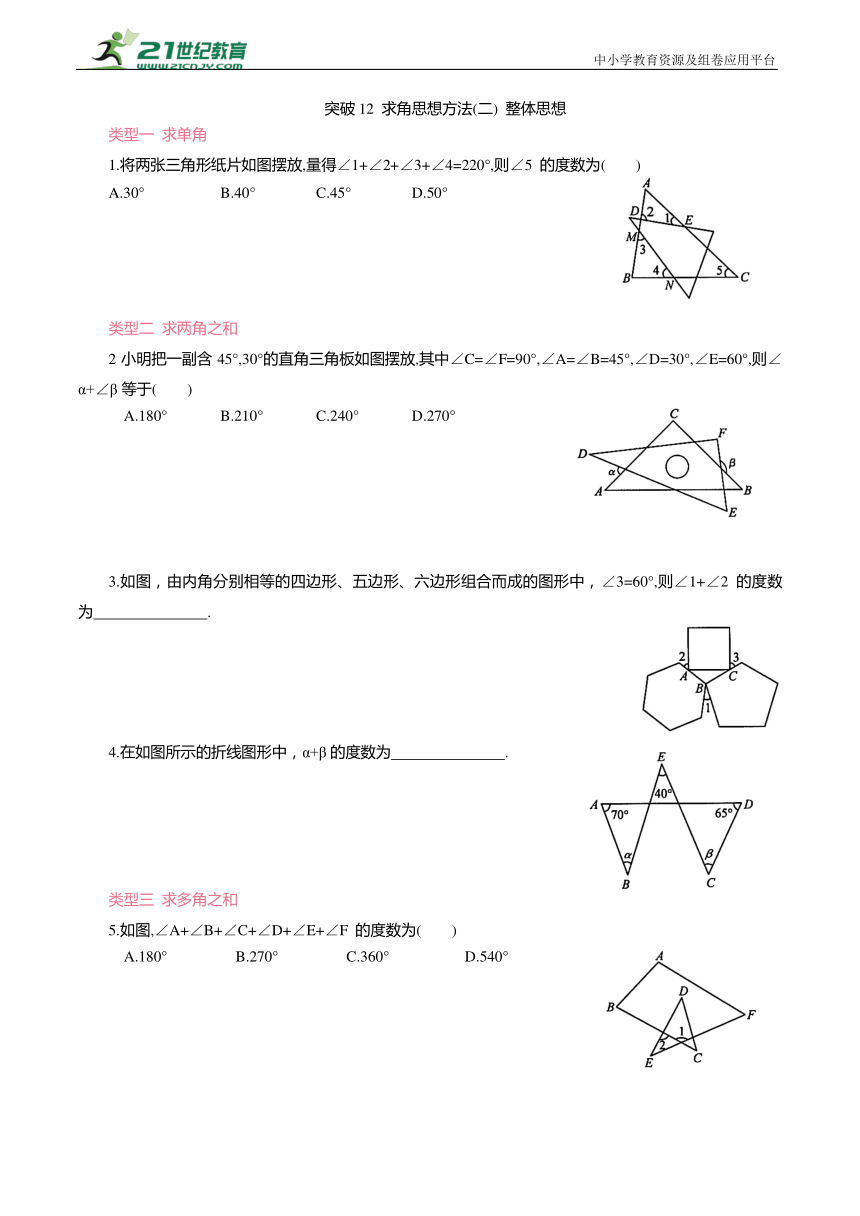
1.如图,BD 是△ABC 的角平分线,AE⊥BD交BD 的延长线于点E, ∠C:∠ADB=2:3,求∠BAC 和∠DAE 的度数.
2.如图,在 中,AH 平分 交BC 于点 H,点 D,E 分别在CA,BA的延长线上,
(1)求证:DB∥EC;
(2)若∠ABD=2∠ABC,∠DAB 比∠AHC 大12°,求∠D 的度数.
类型二 设双元
3.如图,在△ABC 中,BD 平分∠ABC,CE 平分 的邻补角. ,交BA 的延长线于点E,若∠BDC=127°,∠E=44°,则∠BAC 的度数为( )
A.110° B.114° C.118° D.120°
类型三 设多元
4.如图,在△ABC 中, 的三等分线相交于点D,E,F(其中∠CAD=2∠BAD,∠ABE=2∠CBE,∠BCF=2∠ACF),且 的三个内角分别为∠DFE=54°,∠FDE=60°,∠FED=66°,则∠BAC 的度数为( )
A.54° B.60° C.66° D.48°
突破12 求角思想方法(二) 整体思想
类型一 求单角
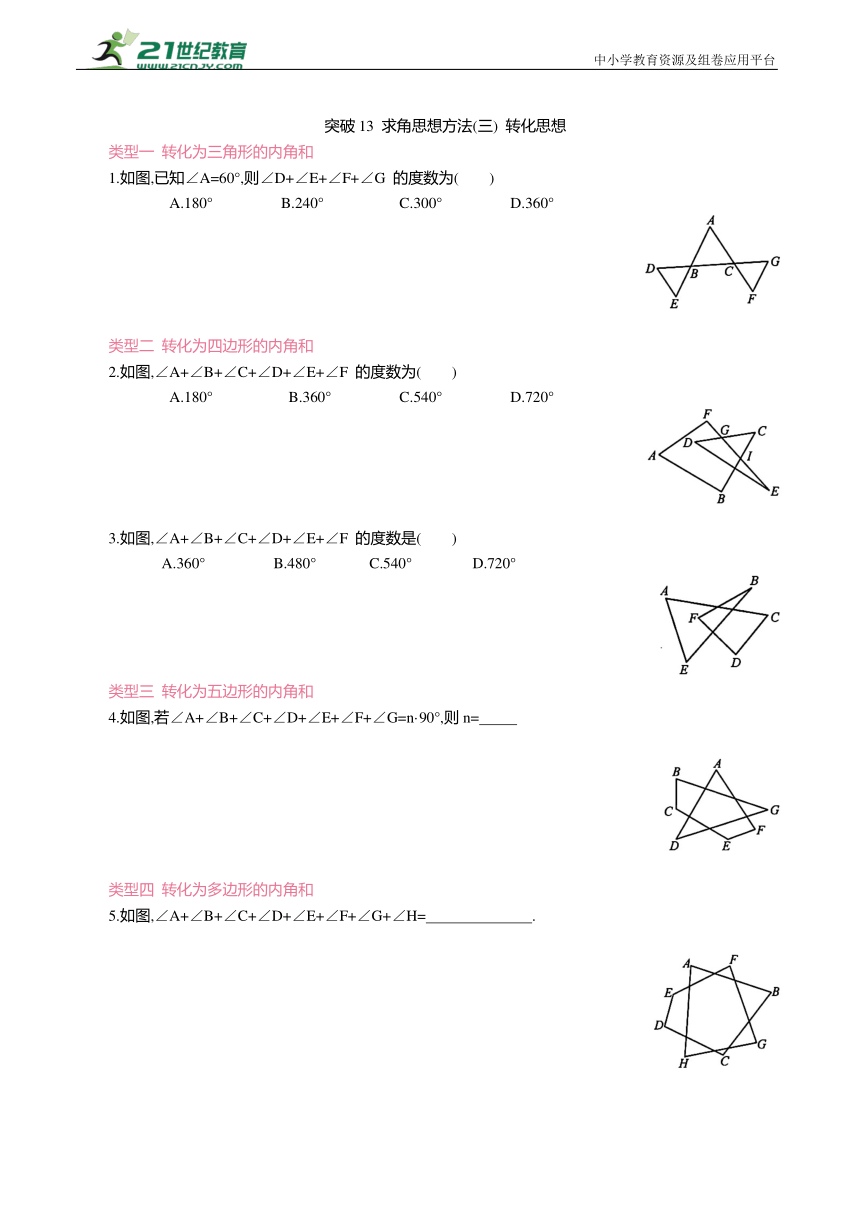
1.将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5 的度数为( )
A.30° B.40° C.45° D.50°
类型二 求两角之和
2小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=∠B=45°,∠D=30°,∠E=60°,则∠α+∠β等于( )
A.180° B.210° C.240° D.270°
3.如图,由内角分别相等的四边形、五边形、六边形组合而成的图形中,∠3=60°,则∠1+∠2的度数为 .
4.在如图所示的折线图形中,α+β的度数为 .
类型三 求多角之和
5.如图,∠A+∠B+∠C+∠D+∠E+∠F 的度数为( )
A.180° B.270° C.360° D.540°
突破13 求角思想方法(三) 转化思想
类型一 转化为三角形的内角和
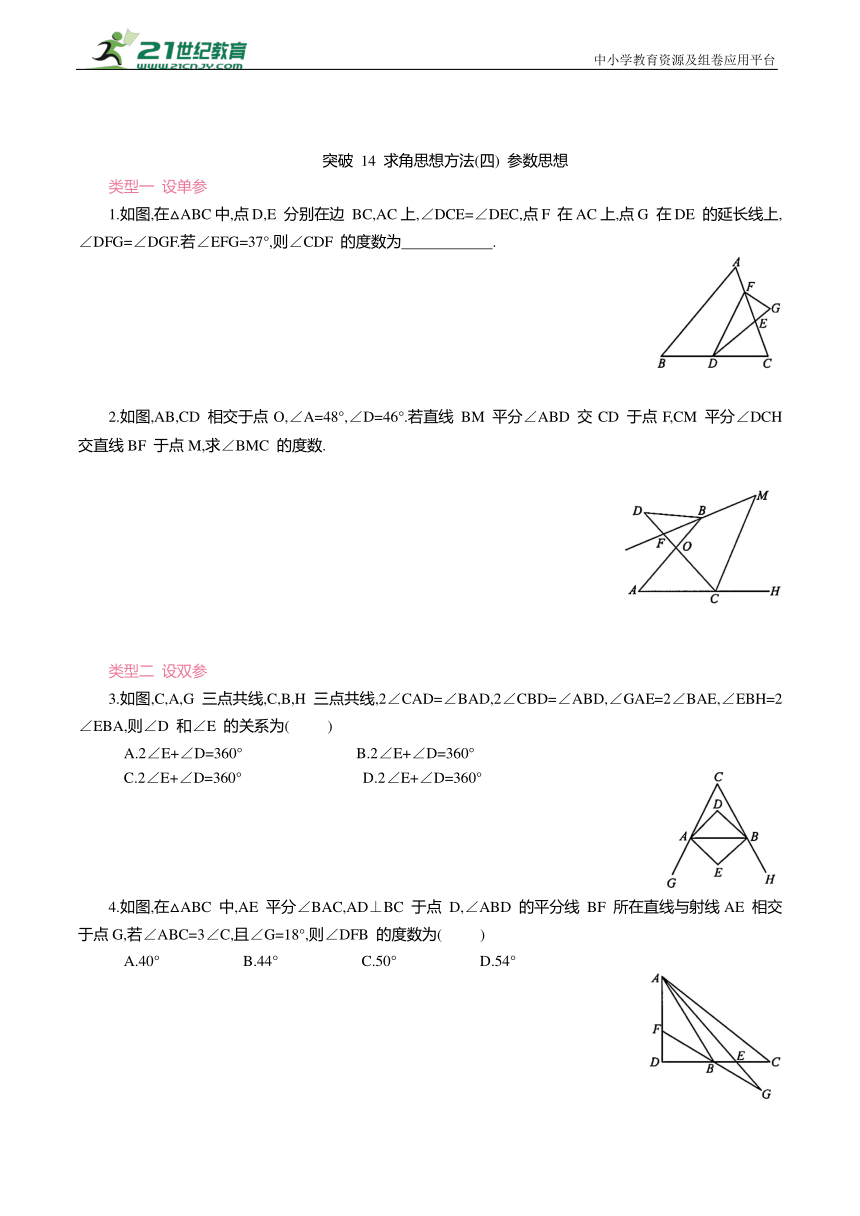
1.如图,已知∠A=60°,则∠D+∠E+∠F+∠G 的度数为( )
A.180° B.240° C.300° D.360°
类型二 转化为四边形的内角和
2.如图,∠A+∠B+∠C+∠D+∠E+∠F 的度数为( )
A.180° B.360° C.540° D.720°
3.如图,∠A+∠B+∠C+∠D+∠E+∠F 的度数是( )
A.360° B.480° C.540° D.720°
类型三 转化为五边形的内角和
4.如图,若∠A+∠B+∠C+∠D+∠E+∠F+∠G=n·90°,则n=
类型四 转化为多边形的内角和
5.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= .
突破 14 求角思想方法(四) 参数思想
类型一 设单参
1.如图,在△ABC中,点D,E 分别在边 BC,AC上,∠DCE=∠DEC,点F 在AC上,点G 在DE 的延长线上,∠DFG=∠DGF.若∠EFG=37°,则∠CDF 的度数为 .
2.如图,AB,CD 相交于点O,∠A=48°,∠D=46°.若直线 BM 平分∠ABD 交CD 于点F,CM 平分∠DCH 交直线BF 于点M,求∠BMC 的度数.
类型二 设双参
3.如图,C,A,G 三点共线,C,B,H 三点共线,2∠CAD=∠BAD,2∠CBD=∠ABD,∠GAE=2∠BAE,∠EBH=2∠EBA,则∠D 和∠E 的关系为( )
A.2∠E+∠D=360° B.2∠E+∠D=360°
C.2∠E+∠D=360° D.2∠E+∠D=360°
4.如图,在△ABC 中,AE 平分∠BAC,AD⊥BC 于点 D,∠ABD 的平分线 BF 所在直线与射线AE 相交于点G,若∠ABC=3∠C,且∠G=18°,则∠DFB 的度数为( )
A.40° B.44° C.50° D.54°
中小学教育资源及组卷应用平台
突破 15 求角思想方法(五) 特殊到一般
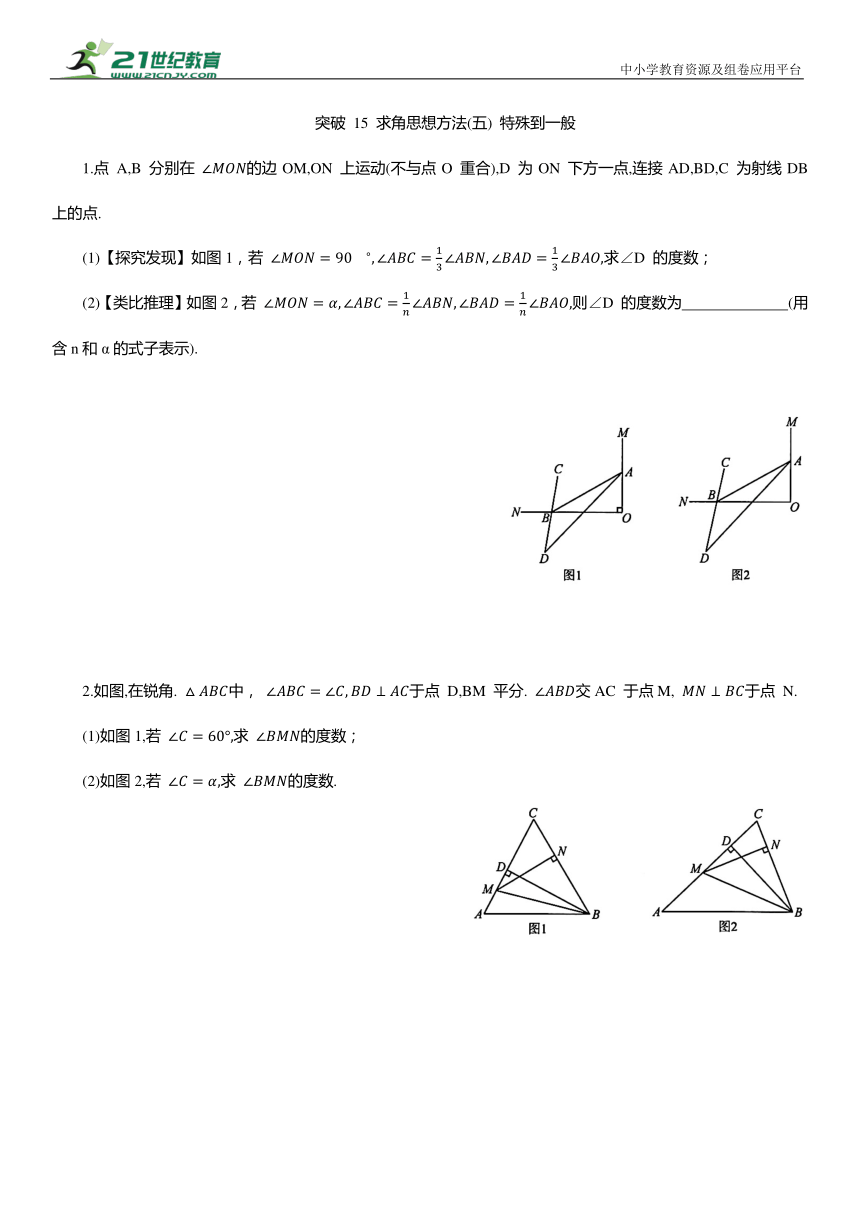
1.点 A,B 分别在 的边OM,ON 上运动(不与点O 重合),D 为ON 下方一点,连接AD,BD,C 为射线DB上的点.
(1)【探究发现】如图1,若 求∠D 的度数;
(2)【类比推理】如图2,若 则∠D 的度数为 (用含n和α的式子表示).
2.如图,在锐角. 中, 于点 D,BM 平分. 交AC 于点M, 于点 N.
(1)如图1,若 求 的度数;
(2)如图2,若 求 的度数.
突破16 求角思想方法(六) 分类讨论
类型一 单高位置不确定
1. AE 是△ABC 的角平分线,AD 是BC 边上的高,且∠B=40°,∠ACD=70°,则∠DAE 的度数为 .
类型二 双高位置不确定
2.在△ABC 中,∠A=55°,BD,CE 是它的两条高,直线BD,CE 交于点F,则∠DFE 的度数为 .
类型三 直角不确定
3.在△ABC中,其中一个内角度数是40°,且∠B=∠C,点 D 在直线BC 边上,连接AD,若△ABD 为直角三角形,则∠ADC 的度数为 .
突破 11 求角思想方法(一)
方程思想
1.解:设∠C=2x,则∠ADB=3x.
∵BD平分∠ABC,∠ABC=72°,
∴∠ABD=∠CBD=36°.
∵∠ADB=∠DBC+∠C,
∴3x=36°+2x,
∴x=36°,
∴∠C=72°,∠ADB=108°,
∴∠BAC=180°-72°-72°=36°.
∵AE⊥BE,
∴∠E=90°.
∵∠ADB=∠E+∠DAE,
∴∠DAE=108°-90°=18°.
2.解:(1)∵DB∥AH,
∴∠D=∠CAH.
∵AH平分∠BAC,
∴∠BAH=∠CAH.
∵∠D=∠E,
∴∠BAH=∠E,
∴AH∥EC,
∴DB∥EC;
(2)设∠ABC=x,
则∠ABD=2x,则∠BAH=2x,
则∠DAB=180°-4x,
则∠AHC = 168°- 4x. 依题意有168°-4x=3x,解得x=24°,
则 ∠D = ∠CAH = ∠BAH =∠ABD=2x=48°.
3. B 解:∵BD 为内角平分线,
∴设∠DBC=∠ABD=x.
∵CE 平分∠ACM,
∴设∠ACE=∠MCE=y.
∵∠ECM=∠ABC+∠E,∠E=44°,
∴y=2x+44°①.
∵∠BDC=127°,
∴∠DBC+∠ACB=53°,
即x+(180°-2y)=53°②.
由①②联立可解得x=13°,
∴∠BAC=∠BDC-∠ABD=127°-13°=114°,故选 B.
4. D 解:∵∠CAD=2∠BAD,∠ABE=2∠CBE,∠BCF=2∠ACF,
∴ 设 ∠BAD = x,∠CBE = y,∠ACF=z,则∠CAF=2x,∠ABD=2y,∠BCE=2z.
∵ ∠DFE = ∠ACF + ∠CAF,∠FDE=∠DAB+∠ABD,∠DEF=∠CBE+∠BCE,
∴54°=2x+z,60°=x+2y,66°=y+2z,
解得x=16°,y=22°,z=22°,∴∠BAC=3x=48°,故选 D.
突破 12 求角思想方法(二)整体思想
1. B 解:在△ADE中,
∵∠A+∠1+∠2=180°,
∴∠A=180°-(∠1+∠2).
∵∠B+∠3+∠4=180°,
∴∠B=180°-(∠3+∠4).
∵∠A+∠B+∠C=180°,
∴180°-(∠1+∠2)+180°-(∠3+∠4)+∠5=180°,
∴∠5=(∠1+∠2+∠3+∠4)-180°.
∵∠1+∠2+∠3+∠4=220°,
∴∠5=220°-180°=40°,故选 B.
2. B 解:∵∠α=∠1,∠β=∠2,
∠C+∠1+∠2+∠E=360°,
∴90°+∠1+∠2+60°=360°,
∴∠1+∠2=210°,
∴∠α+∠β=∠1+∠2=210°.
故选 B.
3.72° 解:∵四边形、五边形、六边形的各内角相等,
∴四边形的每个内角是90°,五边形的每个内角是 108°,六边形的每个内角是120°,
∴∠2+∠BAC=90°,∠1+∠ABC=360°-108°-120°=132°.
∵∠3=60°,
∴∠BCA=180°-60°-90°=30°,
∴∠BAC +∠ABC=180°--30°=150°.
∵∠2+∠BAC+∠1+∠ABC=90°+132°=222°,
∴∠1+∠2=222°-150°=72°.
4.85° 解:连接 BC.
在△EBC中,∠1+∠2=180°-∠E=140°.
在四边形 ABCD 中,∠A+∠ABC+∠BCD+∠D=360°,
∴70°+α+∠1+∠2+β+65°=360°,
∴α+β=360°-70°-65°-140°=85°.
故答案为85°.
5. C 解:∵∠1=∠2+∠E,∠2=∠C+∠D,
∴∠1=∠C+∠D+∠E,
∴∠A+∠B+∠C+∠D+∠E+∠F =∠A +∠B +∠1+∠F =360°.
故选 C.
突破 13 求角思想方法(三)转化思想
1. B 解:∵∠D +∠E =∠ABD,∠ACG=∠F+∠G,
∴∠D+∠E+∠F+∠G=∠ABD+∠ACG.
∵∠ABD=∠A+∠ACB,∠ACG=∠A+∠ABC,
∴∠ABD+∠ACG=∠A+∠ABC+∠ACB+∠A=180°+∠A.
∴∠D+∠E+∠F+∠G=180°+∠A=180°+60°=240°.故选 B.
2. B 解:∵∠D +∠E = ∠EGC,∠EGC+∠C=∠BIG,
∴∠D+∠E+∠C=∠BIG.
故∠A+∠B+∠C+∠D+∠E+∠F=(∠A+∠B+∠F)+(∠D+∠E+∠C)=∠A+∠B+∠F+∠BIG=360°.
故选 B.
3. A 解:连接 DE,则∠B+∠F =∠FDE+∠BED,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.故选 A.
4.6 解:连接 FG,设 AF,DG 交于点H,则∠A+∠D=∠DGF+∠AFG=∠AHG,
∴∠A+∠B+∠C+∠D+∠E+∠AFE +∠BGD =∠B + ∠C +∠E+∠EFG+∠FGB=(5-2)×180°=n·90°,
∴n=6.
5.720° 解:∵∠A+∠B+∠C+∠1=360°,∠F+∠G+∠H+∠2=360°,
∠E+∠D+∠3+∠4=360°,∠2+∠3=180°,∠1+∠4=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°× 3-∠1-∠2-∠3-∠4=360°×3--180°×2=720°.
故答案为720°.
突破 14 求角思想方法(四)参数思想
1.74° 解:设∠DCE=∠DEC=x,
∴∠FEG=x.
∵∠EFG=37°,
∴∠DGF=180°-∠FEG-∠EFG=143°-x,
∴∠DFG=∠DGF=143°-x,
∴∠DFC=∠DFG-EFG=106°-x,
∴∠CDF=180°-∠DFC--∠DCE=180°-(106°-x)-x=74°.
2.解:设∠1=x.
∵BF 平分∠ABD,
∴∠2=∠1=x.
∵∠D=46°,
∴∠BFO=∠D+∠1=46°+x,
∴∠BOC =∠BFO+∠2= 46°+2x.
∵∠A=48°,
∴∠OCA=∠BOC-∠A=2x-2°,
∴∠OCH=180°-∠OCA=182°-2x.
∵CM平分∠DCH,
在 △FMC 中,∠BMC = 180°-∠BFC-∠3=43°.
3. C 解:设∠CAD=x,∠CBD=y,则∠BAD=2x,∠ABD=2y,
∴∠GAB=180°-3x,
∠HBA=180°-3y.
∵∠GAE=2∠BAE,∠EBH=2∠EBA,
∴∠BAE=60°-x,∠EBA=60°-y,
∴∠D=180°-2(x+y),∠E=180°-(60°-x)-(60°-y)=60°+(x+y),
∴2∠E+∠D=360°.故选 C.
4. D 解:∵AE 平分∠BAC,BF 平分∠ABD,
∴∠CAE=∠BAE,∠1=∠2.
设∠CAE =∠BAE=x,∠C=y,∠ABC=3y,
则∠1=∠BAE+∠G=x+18°,
解得y=36°,
∵AD⊥DC,
∴∠D=90°,
∴∠DFB=90°-∠2=54°.
故选 D.
突破 15 求角思想方法(五)特殊到一般
1.解:
∴∠D =∠CBA-∠BAD
∵∠MON=90°,
∴∠D=30°;
∴ ∠D = ∠CBA - ∠BAD =
∵∠MON=α,
2.解:(1)∵∠ABC=∠C=60°,BD⊥AC,
∴∠BDC=90°,
∠CBD=90°-60°=30°,
∴∠ABD=60°-30°=30°.
∵BM平分∠ABD,
∴∠MBN=30°+15°=45°.
∵MN⊥BC,
∴∠MNB=90°,
∴∠BMN=90°-45°=45°;
(2)∵BD⊥AC,MN⊥BC,
∴∠BDC=∠MNB=90°.
∵∠ABC=∠C=α,
∴∠CBD=90°-α,
∴∠ABD=α-(90°-α)=2α-90°.
∵BM平分∠ABD,
90°)=α-45°,
∴∠MBN=α-45°+90°-α=45°,
∴∠BMN=90°-45°=45°.
突破16 求角思想方法(六)分类讨论
1.15°或 35° 解:当高 AD 在△ABC内部时,
∵AD⊥BC,
∴∠ADB=90°.
∵∠B=40°,
∴∠BAD=90°-40°=50°.
∵∠B=40°,∠C=70°,
∴∠BAC=180°-∠B-∠C=70°.
∵AE 是△ABC 角平分线,
∴∠DAE=∠BAD-∠BAE=15°;当高 AD 在△ABC 外部时,同法可得∠DAE = 35°. 故 答 案 为 15°或35°.
2.55°或125° 解:如图1,当△ABC 为锐角三角形时.
∵∠A =55°,BD,CE 是它的两条高,
∴∠DFE=125°;
如图2,图 3,当△ABC 为钝角三角形时.
∵∠A=55°,BD 是它的高,
∴∠ABD=∠EBF=35°.
∵CE 是△ABC 的高,
∴∠DFE=55°.
综上所述,∠DFE=125°或∠DFE=55°.
3.130°或 90°或 20° 解:如图1,若∠B=∠C=40°,且当∠BAD=90°时,∠ADC=130°;
如图 2,若∠B =∠C = 40°,且当∠ADB=90°时,∠ADC=90°;
如图3,若∠BAC=40°,且当∠ADB=90°时,∠ADC=90°;
如图 4,在△ABC 中,若∠BAC =40°,且当∠BAD=90°时,∠ADC=20°.
综上所述,∠ADC 的度数为 130°或90°或 20°.
突破11 求角思想方法(一) 方程思想
类型一 设一元
1.如图,BD 是△ABC 的角平分线,AE⊥BD交BD 的延长线于点E, ∠C:∠ADB=2:3,求∠BAC 和∠DAE 的度数.
2.如图,在 中,AH 平分 交BC 于点 H,点 D,E 分别在CA,BA的延长线上,
(1)求证:DB∥EC;
(2)若∠ABD=2∠ABC,∠DAB 比∠AHC 大12°,求∠D 的度数.
类型二 设双元
3.如图,在△ABC 中,BD 平分∠ABC,CE 平分 的邻补角. ,交BA 的延长线于点E,若∠BDC=127°,∠E=44°,则∠BAC 的度数为( )
A.110° B.114° C.118° D.120°
类型三 设多元
4.如图,在△ABC 中, 的三等分线相交于点D,E,F(其中∠CAD=2∠BAD,∠ABE=2∠CBE,∠BCF=2∠ACF),且 的三个内角分别为∠DFE=54°,∠FDE=60°,∠FED=66°,则∠BAC 的度数为( )
A.54° B.60° C.66° D.48°
突破12 求角思想方法(二) 整体思想
类型一 求单角
1.将两张三角形纸片如图摆放,量得∠1+∠2+∠3+∠4=220°,则∠5 的度数为( )
A.30° B.40° C.45° D.50°
类型二 求两角之和
2小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=∠B=45°,∠D=30°,∠E=60°,则∠α+∠β等于( )
A.180° B.210° C.240° D.270°
3.如图,由内角分别相等的四边形、五边形、六边形组合而成的图形中,∠3=60°,则∠1+∠2的度数为 .
4.在如图所示的折线图形中,α+β的度数为 .
类型三 求多角之和
5.如图,∠A+∠B+∠C+∠D+∠E+∠F 的度数为( )
A.180° B.270° C.360° D.540°
突破13 求角思想方法(三) 转化思想
类型一 转化为三角形的内角和
1.如图,已知∠A=60°,则∠D+∠E+∠F+∠G 的度数为( )
A.180° B.240° C.300° D.360°
类型二 转化为四边形的内角和
2.如图,∠A+∠B+∠C+∠D+∠E+∠F 的度数为( )
A.180° B.360° C.540° D.720°
3.如图,∠A+∠B+∠C+∠D+∠E+∠F 的度数是( )
A.360° B.480° C.540° D.720°
类型三 转化为五边形的内角和
4.如图,若∠A+∠B+∠C+∠D+∠E+∠F+∠G=n·90°,则n=
类型四 转化为多边形的内角和
5.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H= .
突破 14 求角思想方法(四) 参数思想
类型一 设单参
1.如图,在△ABC中,点D,E 分别在边 BC,AC上,∠DCE=∠DEC,点F 在AC上,点G 在DE 的延长线上,∠DFG=∠DGF.若∠EFG=37°,则∠CDF 的度数为 .
2.如图,AB,CD 相交于点O,∠A=48°,∠D=46°.若直线 BM 平分∠ABD 交CD 于点F,CM 平分∠DCH 交直线BF 于点M,求∠BMC 的度数.
类型二 设双参
3.如图,C,A,G 三点共线,C,B,H 三点共线,2∠CAD=∠BAD,2∠CBD=∠ABD,∠GAE=2∠BAE,∠EBH=2∠EBA,则∠D 和∠E 的关系为( )
A.2∠E+∠D=360° B.2∠E+∠D=360°
C.2∠E+∠D=360° D.2∠E+∠D=360°
4.如图,在△ABC 中,AE 平分∠BAC,AD⊥BC 于点 D,∠ABD 的平分线 BF 所在直线与射线AE 相交于点G,若∠ABC=3∠C,且∠G=18°,则∠DFB 的度数为( )
A.40° B.44° C.50° D.54°
中小学教育资源及组卷应用平台
突破 15 求角思想方法(五) 特殊到一般
1.点 A,B 分别在 的边OM,ON 上运动(不与点O 重合),D 为ON 下方一点,连接AD,BD,C 为射线DB上的点.
(1)【探究发现】如图1,若 求∠D 的度数;
(2)【类比推理】如图2,若 则∠D 的度数为 (用含n和α的式子表示).
2.如图,在锐角. 中, 于点 D,BM 平分. 交AC 于点M, 于点 N.
(1)如图1,若 求 的度数;
(2)如图2,若 求 的度数.
突破16 求角思想方法(六) 分类讨论
类型一 单高位置不确定
1. AE 是△ABC 的角平分线,AD 是BC 边上的高,且∠B=40°,∠ACD=70°,则∠DAE 的度数为 .
类型二 双高位置不确定
2.在△ABC 中,∠A=55°,BD,CE 是它的两条高,直线BD,CE 交于点F,则∠DFE 的度数为 .
类型三 直角不确定
3.在△ABC中,其中一个内角度数是40°,且∠B=∠C,点 D 在直线BC 边上,连接AD,若△ABD 为直角三角形,则∠ADC 的度数为 .
突破 11 求角思想方法(一)
方程思想
1.解:设∠C=2x,则∠ADB=3x.
∵BD平分∠ABC,∠ABC=72°,
∴∠ABD=∠CBD=36°.
∵∠ADB=∠DBC+∠C,
∴3x=36°+2x,
∴x=36°,
∴∠C=72°,∠ADB=108°,
∴∠BAC=180°-72°-72°=36°.
∵AE⊥BE,
∴∠E=90°.
∵∠ADB=∠E+∠DAE,
∴∠DAE=108°-90°=18°.
2.解:(1)∵DB∥AH,
∴∠D=∠CAH.
∵AH平分∠BAC,
∴∠BAH=∠CAH.
∵∠D=∠E,
∴∠BAH=∠E,
∴AH∥EC,
∴DB∥EC;
(2)设∠ABC=x,
则∠ABD=2x,则∠BAH=2x,
则∠DAB=180°-4x,
则∠AHC = 168°- 4x. 依题意有168°-4x=3x,解得x=24°,
则 ∠D = ∠CAH = ∠BAH =∠ABD=2x=48°.
3. B 解:∵BD 为内角平分线,
∴设∠DBC=∠ABD=x.
∵CE 平分∠ACM,
∴设∠ACE=∠MCE=y.
∵∠ECM=∠ABC+∠E,∠E=44°,
∴y=2x+44°①.
∵∠BDC=127°,
∴∠DBC+∠ACB=53°,
即x+(180°-2y)=53°②.
由①②联立可解得x=13°,
∴∠BAC=∠BDC-∠ABD=127°-13°=114°,故选 B.
4. D 解:∵∠CAD=2∠BAD,∠ABE=2∠CBE,∠BCF=2∠ACF,
∴ 设 ∠BAD = x,∠CBE = y,∠ACF=z,则∠CAF=2x,∠ABD=2y,∠BCE=2z.
∵ ∠DFE = ∠ACF + ∠CAF,∠FDE=∠DAB+∠ABD,∠DEF=∠CBE+∠BCE,
∴54°=2x+z,60°=x+2y,66°=y+2z,
解得x=16°,y=22°,z=22°,∴∠BAC=3x=48°,故选 D.
突破 12 求角思想方法(二)整体思想
1. B 解:在△ADE中,
∵∠A+∠1+∠2=180°,
∴∠A=180°-(∠1+∠2).
∵∠B+∠3+∠4=180°,
∴∠B=180°-(∠3+∠4).
∵∠A+∠B+∠C=180°,
∴180°-(∠1+∠2)+180°-(∠3+∠4)+∠5=180°,
∴∠5=(∠1+∠2+∠3+∠4)-180°.
∵∠1+∠2+∠3+∠4=220°,
∴∠5=220°-180°=40°,故选 B.
2. B 解:∵∠α=∠1,∠β=∠2,
∠C+∠1+∠2+∠E=360°,
∴90°+∠1+∠2+60°=360°,
∴∠1+∠2=210°,
∴∠α+∠β=∠1+∠2=210°.
故选 B.
3.72° 解:∵四边形、五边形、六边形的各内角相等,
∴四边形的每个内角是90°,五边形的每个内角是 108°,六边形的每个内角是120°,
∴∠2+∠BAC=90°,∠1+∠ABC=360°-108°-120°=132°.
∵∠3=60°,
∴∠BCA=180°-60°-90°=30°,
∴∠BAC +∠ABC=180°--30°=150°.
∵∠2+∠BAC+∠1+∠ABC=90°+132°=222°,
∴∠1+∠2=222°-150°=72°.
4.85° 解:连接 BC.
在△EBC中,∠1+∠2=180°-∠E=140°.
在四边形 ABCD 中,∠A+∠ABC+∠BCD+∠D=360°,
∴70°+α+∠1+∠2+β+65°=360°,
∴α+β=360°-70°-65°-140°=85°.
故答案为85°.
5. C 解:∵∠1=∠2+∠E,∠2=∠C+∠D,
∴∠1=∠C+∠D+∠E,
∴∠A+∠B+∠C+∠D+∠E+∠F =∠A +∠B +∠1+∠F =360°.
故选 C.
突破 13 求角思想方法(三)转化思想
1. B 解:∵∠D +∠E =∠ABD,∠ACG=∠F+∠G,
∴∠D+∠E+∠F+∠G=∠ABD+∠ACG.
∵∠ABD=∠A+∠ACB,∠ACG=∠A+∠ABC,
∴∠ABD+∠ACG=∠A+∠ABC+∠ACB+∠A=180°+∠A.
∴∠D+∠E+∠F+∠G=180°+∠A=180°+60°=240°.故选 B.
2. B 解:∵∠D +∠E = ∠EGC,∠EGC+∠C=∠BIG,
∴∠D+∠E+∠C=∠BIG.
故∠A+∠B+∠C+∠D+∠E+∠F=(∠A+∠B+∠F)+(∠D+∠E+∠C)=∠A+∠B+∠F+∠BIG=360°.
故选 B.
3. A 解:连接 DE,则∠B+∠F =∠FDE+∠BED,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.故选 A.
4.6 解:连接 FG,设 AF,DG 交于点H,则∠A+∠D=∠DGF+∠AFG=∠AHG,
∴∠A+∠B+∠C+∠D+∠E+∠AFE +∠BGD =∠B + ∠C +∠E+∠EFG+∠FGB=(5-2)×180°=n·90°,
∴n=6.
5.720° 解:∵∠A+∠B+∠C+∠1=360°,∠F+∠G+∠H+∠2=360°,
∠E+∠D+∠3+∠4=360°,∠2+∠3=180°,∠1+∠4=180°,
∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°× 3-∠1-∠2-∠3-∠4=360°×3--180°×2=720°.
故答案为720°.
突破 14 求角思想方法(四)参数思想
1.74° 解:设∠DCE=∠DEC=x,
∴∠FEG=x.
∵∠EFG=37°,
∴∠DGF=180°-∠FEG-∠EFG=143°-x,
∴∠DFG=∠DGF=143°-x,
∴∠DFC=∠DFG-EFG=106°-x,
∴∠CDF=180°-∠DFC--∠DCE=180°-(106°-x)-x=74°.
2.解:设∠1=x.
∵BF 平分∠ABD,
∴∠2=∠1=x.
∵∠D=46°,
∴∠BFO=∠D+∠1=46°+x,
∴∠BOC =∠BFO+∠2= 46°+2x.
∵∠A=48°,
∴∠OCA=∠BOC-∠A=2x-2°,
∴∠OCH=180°-∠OCA=182°-2x.
∵CM平分∠DCH,
在 △FMC 中,∠BMC = 180°-∠BFC-∠3=43°.
3. C 解:设∠CAD=x,∠CBD=y,则∠BAD=2x,∠ABD=2y,
∴∠GAB=180°-3x,
∠HBA=180°-3y.
∵∠GAE=2∠BAE,∠EBH=2∠EBA,
∴∠BAE=60°-x,∠EBA=60°-y,
∴∠D=180°-2(x+y),∠E=180°-(60°-x)-(60°-y)=60°+(x+y),
∴2∠E+∠D=360°.故选 C.
4. D 解:∵AE 平分∠BAC,BF 平分∠ABD,
∴∠CAE=∠BAE,∠1=∠2.
设∠CAE =∠BAE=x,∠C=y,∠ABC=3y,
则∠1=∠BAE+∠G=x+18°,
解得y=36°,
∵AD⊥DC,
∴∠D=90°,
∴∠DFB=90°-∠2=54°.
故选 D.
突破 15 求角思想方法(五)特殊到一般
1.解:
∴∠D =∠CBA-∠BAD
∵∠MON=90°,
∴∠D=30°;
∴ ∠D = ∠CBA - ∠BAD =
∵∠MON=α,
2.解:(1)∵∠ABC=∠C=60°,BD⊥AC,
∴∠BDC=90°,
∠CBD=90°-60°=30°,
∴∠ABD=60°-30°=30°.
∵BM平分∠ABD,
∴∠MBN=30°+15°=45°.
∵MN⊥BC,
∴∠MNB=90°,
∴∠BMN=90°-45°=45°;
(2)∵BD⊥AC,MN⊥BC,
∴∠BDC=∠MNB=90°.
∵∠ABC=∠C=α,
∴∠CBD=90°-α,
∴∠ABD=α-(90°-α)=2α-90°.
∵BM平分∠ABD,
90°)=α-45°,
∴∠MBN=α-45°+90°-α=45°,
∴∠BMN=90°-45°=45°.
突破16 求角思想方法(六)分类讨论
1.15°或 35° 解:当高 AD 在△ABC内部时,
∵AD⊥BC,
∴∠ADB=90°.
∵∠B=40°,
∴∠BAD=90°-40°=50°.
∵∠B=40°,∠C=70°,
∴∠BAC=180°-∠B-∠C=70°.
∵AE 是△ABC 角平分线,
∴∠DAE=∠BAD-∠BAE=15°;当高 AD 在△ABC 外部时,同法可得∠DAE = 35°. 故 答 案 为 15°或35°.
2.55°或125° 解:如图1,当△ABC 为锐角三角形时.
∵∠A =55°,BD,CE 是它的两条高,
∴∠DFE=125°;
如图2,图 3,当△ABC 为钝角三角形时.
∵∠A=55°,BD 是它的高,
∴∠ABD=∠EBF=35°.
∵CE 是△ABC 的高,
∴∠DFE=55°.
综上所述,∠DFE=125°或∠DFE=55°.
3.130°或 90°或 20° 解:如图1,若∠B=∠C=40°,且当∠BAD=90°时,∠ADC=130°;
如图 2,若∠B =∠C = 40°,且当∠ADB=90°时,∠ADC=90°;
如图3,若∠BAC=40°,且当∠ADB=90°时,∠ADC=90°;
如图 4,在△ABC 中,若∠BAC =40°,且当∠BAD=90°时,∠ADC=20°.
综上所述,∠ADC 的度数为 130°或90°或 20°.
