构造全等三角形专项练习(含解析)2024-2025学年人教版八年级数学上册
文档属性
| 名称 | 构造全等三角形专项练习(含解析)2024-2025学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 766.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 09:52:06 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
突破 10 构全等(一) 知中点
类型一 倍长中线证不等关系
1.如图,在 中,AD 为BC边上的中线,E,F 分别为AB,AC上的点,且ED⊥FD,连接EF.求证:1
类型二 作垂线构全等
2.如图,在 中, ,直线 l经过边AB 的中点D,与 BC 交于点M,分别过点A,C作直线l 的垂线,垂足为E,F,则. 的最大值为( )
A.8 B.6 C.4 D.12
类型三 倍长中线证二倍关系
3.如图,点. ,P是y 轴正半轴上一动点,C是 AP 的中点,D 是x 轴正半轴上一点,且.
(1)求证:
(2)求点 D 的坐标.
类型四 知平行,间接倍长中线
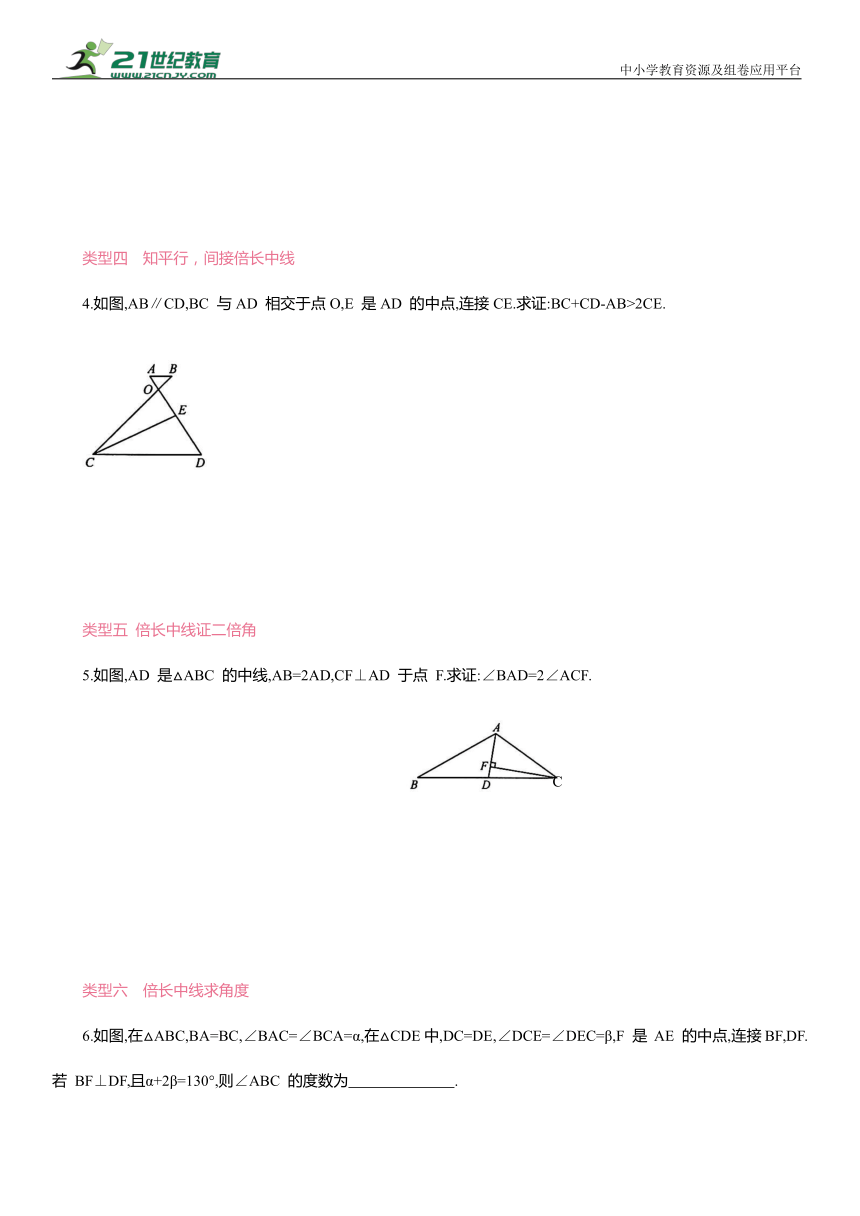
4.如图,AB∥CD,BC 与AD 相交于点O,E 是AD 的中点,连接CE.求证:BC+CD-AB>2CE.
类型五 倍长中线证二倍角
5.如图,AD 是△ABC 的中线,AB=2AD,CF⊥AD 于点 F.求证:∠BAD=2∠ACF.
C
类型六 倍长中线求角度
6.如图,在△ABC,BA=BC,∠BAC=∠BCA=α,在△CDE中,DC=DE,∠DCE=∠DEC=β,F 是 AE 的中点,连接BF,DF.若 BF⊥DF,且α+2β=130°,则∠ABC 的度数为 .
突破11 构全等(二) 证中点
类型一 找全等,证中点
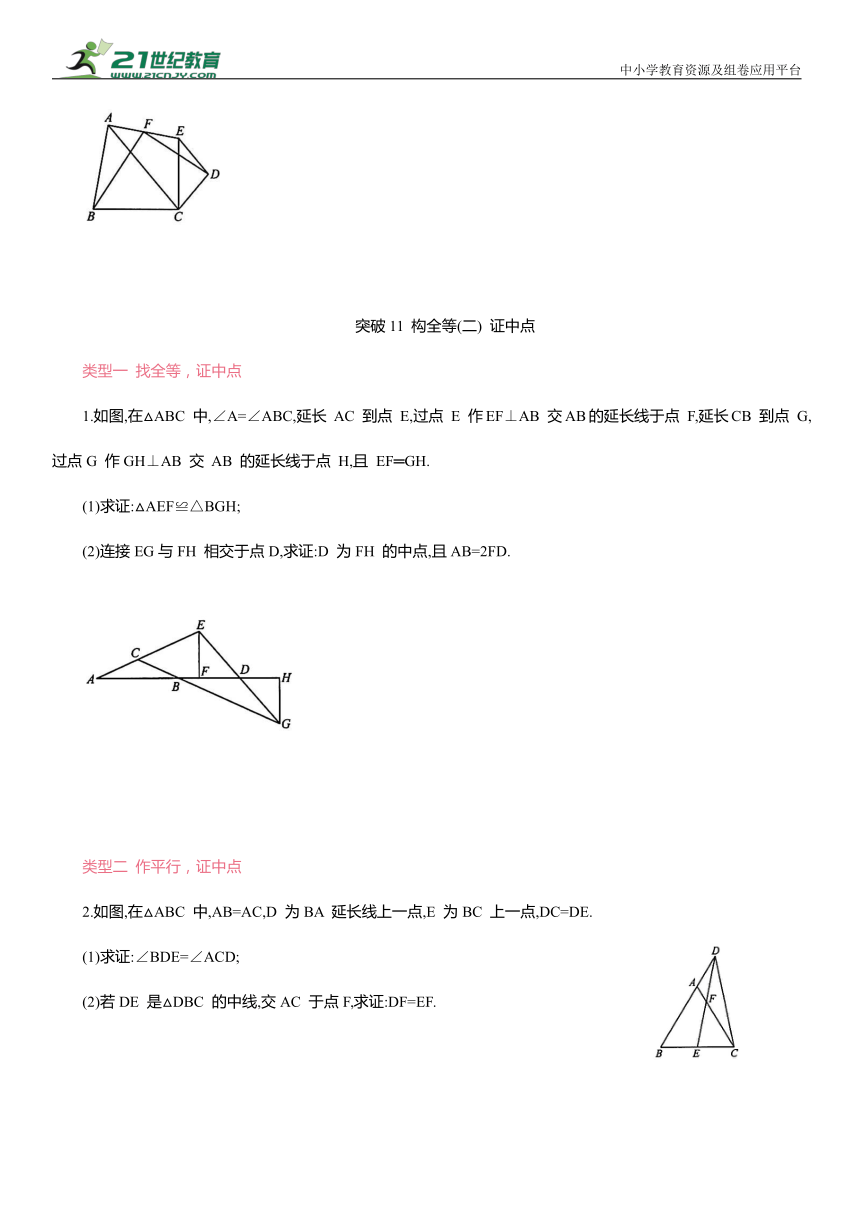
1.如图,在△ABC 中,∠A=∠ABC,延长 AC 到点 E,过点 E 作EF⊥AB 交AB的延长线于点 F,延长CB 到点 G,过点G 作GH⊥AB 交 AB 的延长线于点 H,且 EF═GH.
(1)求证:△AEF≌△BGH;
(2)连接EG与FH 相交于点D,求证:D 为FH 的中点,且AB=2FD.
类型二 作平行,证中点
2.如图,在△ABC 中,AB=AC,D 为BA 延长线上一点,E 为BC 上一点,DC=DE.
(1)求证:∠BDE=∠ACD;
(2)若DE 是△DBC 的中线,交AC 于点F,求证:DF=EF.
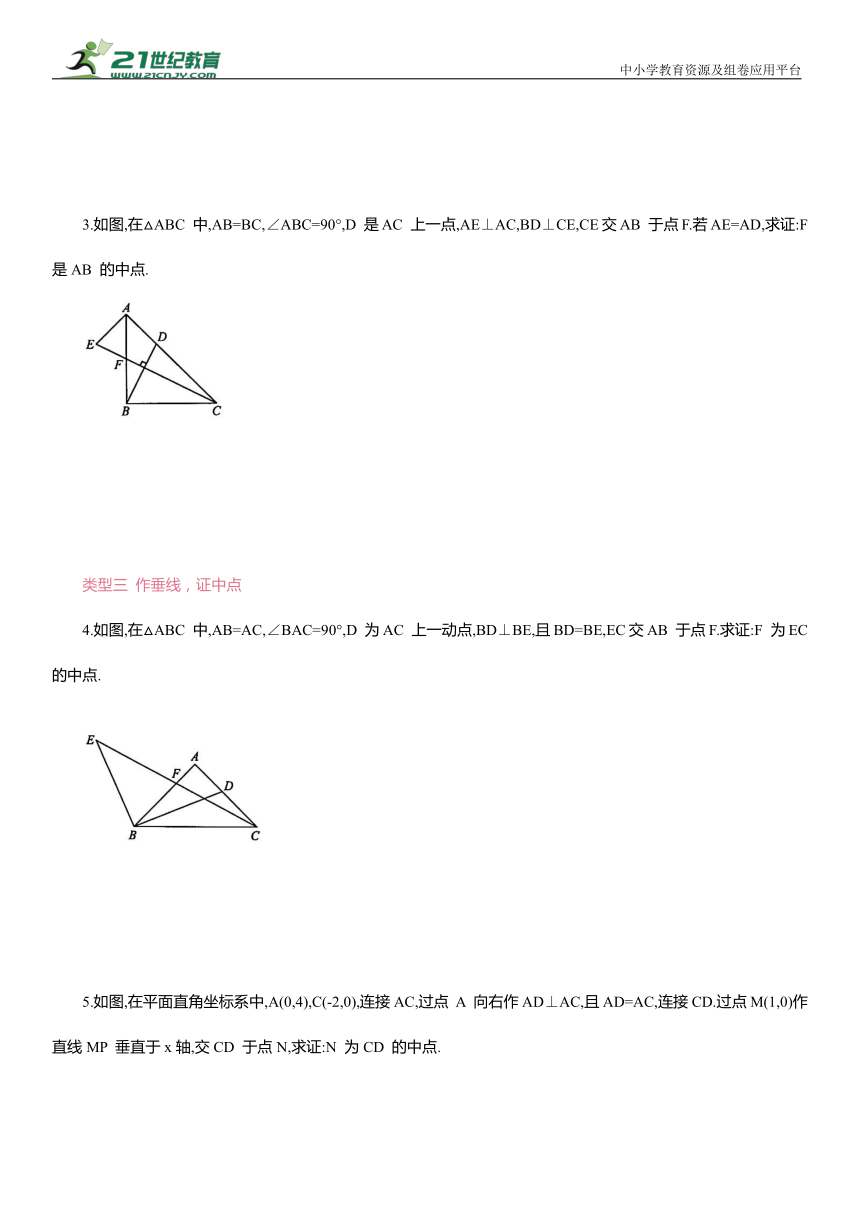
3.如图,在△ABC 中,AB=BC,∠ABC=90°,D 是AC 上一点,AE⊥AC,BD⊥CE,CE交AB 于点F.若AE=AD,求证:F是AB 的中点.
类型三 作垂线,证中点
4.如图,在△ABC 中,AB=AC,∠BAC=90°,D 为AC 上一动点,BD⊥BE,且BD=BE,EC交AB 于点F.求证:F 为EC 的中点.
5.如图,在平面直角坐标系中,A(0,4),C(-2,0),连接AC,过点 A 向右作AD⊥AC,且AD=AC,连接CD.过点M(1,0)作直线MP 垂直于x轴,交CD 于点N,求证:N 为CD 的中点.
6.如图,D 是△ABC 的边BC 的延长线上一点,点 E 在边AC 上,AB=DE,∠BAC=∠DEC.求证:CD=BC.
突破12 构全等(三) 截长补短
类型一 直接截长
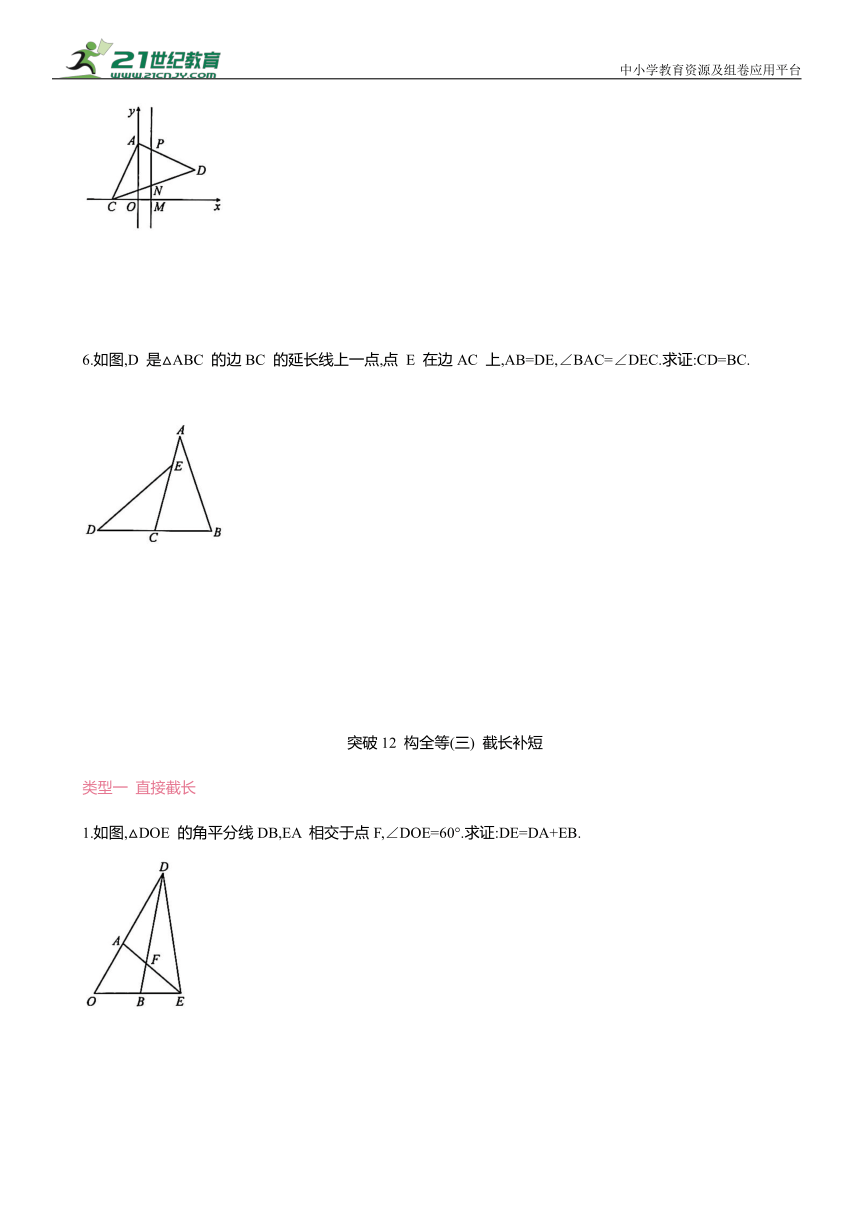
1.如图,△DOE 的角平分线DB,EA 相交于点F,∠DOE=60°.求证:DE=DA+EB.
类型二 直接补短
2.如图,在 Rt△ABC 中,∠ABC=90°,以 AC 为边作△ACD,满足 AD=AC,E 为BC 上一点,且 连接DE.求证:DE=CE+2BE.
3.如图,在△ABC中,AB=AC,∠BAC>90°,BD⊥AC,垂足为D,点E在AD上,BE 平分∠ABD,点 F 在BD 延长线上,BF=CE,延长FE 交BC 于点H.
(1)求证:∠CBE=45°;
(2)写出线段 BH 和EH 的位置关系和数量关系,并证明.
4.如图,在△ABC 中,∠BAC=30°,AD 平分∠BAC,点 E 在 BC 的延长线上,∠CAE=75°.若CE=BA+AC,求∠B 的度数.
类型三 间接截长(补短)
5.如图,在四边形 ABDC 中,∠D=∠B=90°,O 为 BD 上的一点,且 AO平分∠BAC,CO平分∠ACD.求证:AB+CD=AC.
6.如图,BN 为∠MBC 的平分线,P 为BN 上一点,且 PD⊥BC 于点 D,∠APC+∠ABC=180°.
(1)求证:PA=PC;
(2)求证:BC-AB=2CD.
C
突破 13 构全等(四) 面积巧转化
类型一 全等割补
1.如图,在四边形ABCD 中,AD∥BC,E 是CD 的中点,EF⊥AB 于点F,AB=10,EF=4,则四边形ABCD 的面积为 .
类型二 全等拼接
2.如图,在 Rt△ABC 中,∠ABC=90°,BD 是△ABC 的角平分线,DE⊥AB 于点E,DF⊥BC 于点F,AD=6,CD=10,则S△ADE+ S△CDF的值为 .
类型三 作高计算
3.如图,在△ABC 中,∠BAC=90°,AB=AC,BD 是△ABC 的角平分线,若BD=8,求△BDC 的面积.
C
类型四 角分垂,出中点
4.如图,在△ABC 中,AD 平分∠BAC,BD⊥AD,连接CD,若 则S△ABC的值为 .
类型五 三垂直,用和差
5.如图,在△ABC 中,AB=AC,∠BAC=90°,M 是△ABC外一点,AM⊥CM,N是BM上一点,AN⊥CN,若AM=10,AN=7,则△AMN的面积为 .
C
类型六 手拉手,构巧图
6.如图,D 为△ABC 内一点,CD⊥BD,CD=BD,∠BAD=45°,AB=12.求
类型七 平行出,等积现
7.如图,在长方形ABCD 中,E,F 分别是边AD,AB 上的点,BE,DF 交于点O,BE=DF,连接OC.求证:OC平分∠BOD.
类型八 构双高,求长度
8.如图,在正方形ABCD 中,E 是正方形内一点,AE⊥BE,连接DE,CF⊥DE 于点 F,EF=2,DF=5.
(1)求△AED 的面积;
(2)求 AE 的长.
突破10 构全等(一) 知中点
1.证明:延长 ED 至点 G,使 DG =DE,连接GC,GF.
∵AD 是BC上的中线,
∴BD=CD.
在△BDE 与△CDG 中,
∴△BDE≌△CDG(SAS),
∴BE=CG.
∵ED⊥FD,
∴∠EDF=∠GDF=90°.
∵DE=DG,DF=DF,
∴△EDF≌△GDF(SAS),
∴EF=FG.
在△FCG 中,
∵GC+FC>FG,
∴BE+FC>EF.
2. B 解:过点 B 作BG⊥l于点G.
∵AE⊥l,
∴∠AED=∠BGD=90°.
∵D是边AB 的中点,
∴AD=BD,
∴△AED≌△BGD(AAS),
∴AE=BG.
∵CF⊥l,BG⊥l,
∴CF≤CM,BG≤BM,
∴AE+CF=BG+CF≤BM+CM,即AE+CF≤BC,
∴当点C,F,G,B共线时,AE+CF有最大值,最大值为 BC 的长.
∵BC=6,
∴AE+CF 的最大值为6.故选 B.
3.解:(1)延长 BC 到点 E,使 CE=BC,连接 PE,过点 E 作 EF⊥x 轴于点F.
∵C 是PA 的中点,
∴PC=AC,
∴△ABC≌△PEC,
∴∠ABC=∠PEC,
∴PE∥AB.
∵EF⊥x轴,
∴PO=EF.
∵∠POD=∠EFB=90°,∠PDO=∠CBA,
∴△POD≌△EFB,
∴PD=BE=2BC;
(2)由(1)得 PE=AB=OF=5-2=3,OD=BF=BO+OF=5+3=8,
∴D(8,0).
4.证明:延长CE 交AB 的延长线于点F.
∵E为AD 的中点,
∴AE=ED.
∵AB∥CD,
∴∠F=∠DCE,∠A=∠D,
∴△AFE≌△DCE,
∴AF=CD,CE=EF,
∴CF=2CE,
BF=AF-AB=CD-AB.
在△BCF 中,BC+BF>CF=2CE,∴BC+CD-AB>2CE.
5.证明:延长 AD 至点 E,使 DE =AD,连接 CE,过点 E 作 EH⊥AC于点 H.
∵AD 是△ABC的中线,
∴CD=BD.
在△CDE 和△BDA 中,
∴△CDE≌△BDA(SAS),
∴CE=AB=2AD=AE,∠BAD=∠AEC.
∵EH⊥AC,
∴∠AHE=∠CHE=90°.
∵CE=AE,HE=HE,
∴Rt△AHE≌△Rt△CHE(HL),
∴∠AEH=∠CEH,
∴∠BAD=∠AEC=2∠AEH.
∵CF⊥AD,
∴∠AFC=∠AHE=90°,
∴∠ACF + ∠CAF = ∠AEH +∠CAF=90°,
∴∠ACF=∠AEH,
∴∠BAD=2∠ACF.
6.80° 解:延长 DF 到点G,使 FG=DF,连接AG,BG,BD,
设∠AGF=x,∠AGB=y.
∵F 是AE 的中点,
∴AF=EF.
∵∠AFG=∠EFD,
∴△AFG≌△EFD(SAS),
∴∠AGF=∠EDF=x,AG=ED.
∵BF⊥DF,
∴BF 是 DG 的垂直平分线,
∴BG=BD,
∴∠BDG = ∠BGD = ∠AGB +∠AGF=x+y.
∵AB=BC,
∴△BAG≌△BCD(SSS),
∴∠AGB=∠CDB=y,∠ABG=∠CBD,
∴∠EDC = ∠EDG + ∠BDG +∠CDB=x+x+y+y=2x+2y.
∵∠ABG=∠CBD,
∴∠ABG + ∠ABD = ∠CBD +∠ABD,
∴∠DBG=∠ABC.
∵ ∠BAC + ∠BCA = 180° ∠ABC,∠BDG+∠BGD=180°—∠DBG,∠BAC=∠BCA=α,
∴∠BAC + ∠BCA = ∠BDG +∠BGD=2α,
∴2(x+y)=2α,
∴x+y=α.
∵∠DCE=∠DEC=β,∠DCE+∠DEC+∠EDC=180°,
∴2β+2x+2y=180°,
∴2β+2α=180°.
∵α+2β=130°,
∴∠BAC=∠BCA=50°,
∴∠ABC=180°—∠BAC-∠BCA=80°.故答案为80°.
突破 11 构全等(二) 证中点
1.证明:(1)∵∠A=∠ABC,∠ABC=∠GBH,
∴∠A=∠GBH.
∵EF⊥AB,GH⊥AB,
∴∠AFE=∠BHG.
∵EF=GH,
∴△AEF≌△BGH(AAS);
(2)∵△AEF≌△BGH,
∴AF=BH,
∴AB=FH.
∵EF⊥AB,GH⊥AB,
∴∠EFD=∠GHD.
∵∠EDF=∠GDH,EF=GH,
∴△EFD≌△GHD(AAS),
∴D为FH的中点,且AB=2FD.
2.证明:(1)∵DC=DE,
∴∠DEC=∠DCE.
∵∠DEC=∠BDE+∠B,∠DCE=∠ACB+∠ACD,
∴ ∠BDE + ∠B = ∠ACB +∠ACD.
∵AB=AC,
∴∠B=∠ACB,
∴∠BDE=∠ACD.
(2)作 EG∥CD 交CA 的延长线于点G, 则 ∠CEG + ∠DCE = 180°,∠FCD=∠G.
∵∠BED+∠DEC=180°,
且∠DCE=∠DEC,
∴∠CEG=∠BED.
∵DE 是△DBC 的中线,
∴CE = BE. 在 △CEG 和△BED
中
∴△CEG≌△BED(ASA),
∴GE=DE,
∴DC = GE. 在△CFD 和△GFE
中,
∴△CFD≌△GFE(AAS),
∴DF=EF.
3.证明:过点 B 作 BH∥AE,交 CE 于点 H.
∵AB=BC,∠ABC=90°,BD⊥CE,
∴∠ABD + ∠CBD = ∠CBD +
∴∠ABD=∠BCH.
∵AE⊥AC,∠BAC=∠ACB=45°,
∴∠EAB=∠BAC=∠ACB=45°.
∵BH∥AE,
∴∠ABH=∠EAB=45°,
∠BAD,
∴△ABD≌△BCH(ASA),
∴BH=AD=AE.
∵∠ABH=∠EAB,∠AFE=∠BFH,
∴△AEF≌△BHF(AAS),
∴AF=BF,
∴F 是 AB 的中点.
4.证明:过点 E 作 EH⊥AB 于点 H.
∵BD⊥BE,
∴∠EBD=∠EHB=∠BAC=90°,
∴∠BEH + ∠EBH = ∠ABD +∠EBH=90°,
∴∠BEH=∠ABD.
又∵BD=BE,
∴△BEH≌∠DBA(AAS),
∴EH=AB=AC,
∴△EFH≌△CFA(AAS),
∴EF=CF,即 F 为EC的中点.
5.证明:过点 D 作 DH⊥y 轴,垂足为H,HD 交MP 于点S.
则∠AHD=90°.
∵A(0,4),C(-2,0),
∴CO=2.
∵AD⊥AC,
∴∠CAD=90°,
∴∠CAO+∠DAH=90°.
又∵∠CAO+∠ACO=90°,
∴∠ACO=∠DAH,
∴△CAO≌△ADH(AAS),
∴HD=AO=4.
∵M(1,0),MP 垂直于x 轴,DH⊥y轴,
∴MO=HS=1,∠NMC=∠NSD=90°,
∴DS=HD-HS=4-1=3,CM=CO+OM=2+1=3,
∴DS=CM,
∴△NSD≌△NMC(AAS),
∴CN=ND,即 N 为CD 的中点.
6.证明:分别过点 B,D 作AC 的垂线,垂足分别为G,F,
∵∠BAC=∠DEC,AB=DE,
∴△ABG≌△EDF,
∴BG=DF,
∵∠DFC=∠BGC=90°,∠DCF=∠BCG,
∴△DCF≌△BCG,
∴CD=BC.
突破 12 构全等(三) 截长补短
1.证明:∵∠DOE=60°,
∴∠ODE+∠OED=120°.
∵ DB, EA 分 别 平 分 ∠ODE,∠OED,
∠ODE)=60°,
∴∠AFD=60°,
∴∠BFE=∠AFD=60°.
在 DE上截取DH=DA,连接 FH,则△DAF≌△DHF(SAS),
∴∠DFA=∠DFH,
∴∠DFH=60°,
∴∠EFH=∠EFB.
∵EF=EF,∠HEF=∠BEF,
∴△HFE≌△BFE(ASA),
∴EH=EB.
∵DE=DH+EH,
∴DE=DA+EB.
2.证明:延长EB 至G,使 BG=BE,连接 AG.
∵∠ABC=90°,
∴∠ABG=90°,
∴△GAB≌△EAB(SAS),
∴AG=AE,
∴∠GAE=∠CAD,
∴∠GAE + ∠EAC = ∠CAD +∠EAC,
∴∠GAC = ∠EAD. 在△GAC 与△EAD中,
∴△GAC≌△EAD(SAS),
∴CG=DE.
∵CG=CE+GE=CE+2BE,
∴DE=CE+2BE.
3.解:(1)∵BD⊥AC 于点D,
∴∠BDC=∠FDC=90°,
∴∠DAB+∠DBA=90°.
∵AB=AC,
∴∠ABC=∠C,
∴ ∠DAB = ∠ABC + ∠C =2∠ABC,
∵BE 平分∠ABD,
∴∠CBE = ∠ABC + ∠ABE =
(2)BH⊥EH,BH=EH.理由如下:延长BA 到点G,使AG=AE,连接 EG.
∵AB=AC,
∴AB+AG=AC+AE,
∴BG=CE.
∵BF=CE,
∴BG=BF.
在△EBG 和△EBF 中,
∴△EBG≌△EBF(SAS),
∴∠G=∠F.
∵∠G=∠AEG,
∴∠DAB=∠G+∠AEG=2∠G,
∴∠G=∠C,
∴∠F=∠C.
∵∠HEC=∠DEF,
∴∠BHE=∠C+∠HEC=∠F+
∴BH⊥EH.
∵∠HEB=∠HBE=45°,
∴BH=EH.
4.解:延长CA 至点O,使AO=AB,连接 OE.
∵∠BAC=30°,∠CAE=75°,
∴∠BAE =∠OAE. 在△AOE 和△ABE 中,
∴△AOE≌△ABE(SAS),
∴∠B=∠O.
∵CE=BA+AC,
∴CE=AO+AC=OC,
∴∠O=∠CEO,
∴∠OCE+∠O+∠OEC=∠B+∠BAC+∠B+∠B=180°,故 ∴∠B=50°.
5.证明:过点 O 作OE⊥AC于点E.
∵∠D=∠B=90°,
∴OB⊥AB,OD⊥CD,
∵ AO 平 分 ∠BAC, CO 平 分∠ACD,
∴OB=OE,OD=OE.
∵OA=OA,OC=OC,
∴Rt△OAB≌Rt△OAE(HL), Rt△OCE≌Rt△OCD(HL),
∴AB=AE,CD=CE,
∴AB+CD=AE+CE=AC.
6.证明:(1)过点 P 作 PK⊥AB,垂足为 K.
∵PK⊥AB,PD⊥BC,∠ABP=∠CBP,
∴PK=PD,
∴Rt△BPK≌Rt△BPD(HL),
∴BK=BD.
∵∠APC+∠ABC=180°,∠ABC+∠KPD=180°,
∴∠KPD=∠APC,
∴∠APK=∠CPD,
∴△PAK≌△PCD(ASA),
∴AK=CD,PA=PC;
(2)∵BK=BD,AK=CD,
∴BC-AB=CD+BD-AB=CD+BK-AB=2CD.
突破 13 构全等(四)面积巧转化
1.40 解:延长 AE 交 BC 的延长线于点 H,连接 BE.
∵E是CD的中点,
∴DE=CE,
∵AD∥BC,
∴∠D=∠DCH,
∵∠AED=∠HEC,
∴△ADE≌△HCE,
∴AE=EH,S四边形ABCD =S△ABH =2S△AEB=AB·EF=40.
2.30 解:在 FB上截取FH=AE,连接 DH.
∵BD 平分∠ABC,DE⊥AB 于点E,DF⊥BC于点F,
∴DE=DF,
∴△ADE≌△HDF,
∴AD=DH=6,
∠ADE=∠HDF,
∴∠HDF+∠CDF=90°,即∠HDC=90°,
3.解:过点 C 作CF⊥BD 交 BD 的延长线于点 E,交BA 的延长线于点F.
∵BD平分∠ABC,
∴∠FBE=∠CBE,
∴△BFE≌△BCE,
∴CE=EF,
∵AB=AC,∠ABD=∠ACF,
∴△ABD≌△ACF,
∴BD=CF=2CE=8,
16.
4.14 解:延长 BD 交AC 的延长线于点E.
∵AD 平分∠BAC,BD⊥AD,
∴△ABD≌△AED,
∴BD=DE,
设
则 =7+x,
∴S△ABE=2S△AED=14+2x,
-2x=14.
5.25.5 解:过点 B 作BE⊥AN 于点E,过点 B 作 BF⊥AM 于点 F,
∵AB=AC,∠BAC=90°,
AN⊥CN,AM⊥CM,
△ABE≌△CAN,
△ABF≌△CAM,
∴BE=AN=7,
∴BF=AM=10,
6.解:过点 D 作DE⊥AD 交AB 于点E,
∵∠BAD=45°,
∴△ADE 为等腰直角三角形,
∴AD=DE,
∵BD=CD,BD⊥CD,
∴△ABD≌△ECD,
∴AB=CE=12,
∠BAD=∠CED=45°,
∴∠AEC=90°,
7.证明:连接 CF,CE,过点 C 分别作CG⊥BE 于点G,CH⊥DF 于点 H,
长方形ABCD,
又∵BE=DF,
∴CG=CH,
∴OC 平分∠BOD.
8.解:(1)过点A 作AH⊥DE 于点H,
∵AD=CD,AD⊥CD,
∴△ADH≌△DCF,
∴AH=DF=5,
(2)过点 D 作 DG⊥AE 于点G,
∵AB=AD,AD⊥AB,
∴△ABE≌△DAG,
∴AE=DG,
突破 10 构全等(一) 知中点
类型一 倍长中线证不等关系
1.如图,在 中,AD 为BC边上的中线,E,F 分别为AB,AC上的点,且ED⊥FD,连接EF.求证:1
类型二 作垂线构全等
2.如图,在 中, ,直线 l经过边AB 的中点D,与 BC 交于点M,分别过点A,C作直线l 的垂线,垂足为E,F,则. 的最大值为( )
A.8 B.6 C.4 D.12
类型三 倍长中线证二倍关系
3.如图,点. ,P是y 轴正半轴上一动点,C是 AP 的中点,D 是x 轴正半轴上一点,且.
(1)求证:
(2)求点 D 的坐标.
类型四 知平行,间接倍长中线
4.如图,AB∥CD,BC 与AD 相交于点O,E 是AD 的中点,连接CE.求证:BC+CD-AB>2CE.
类型五 倍长中线证二倍角
5.如图,AD 是△ABC 的中线,AB=2AD,CF⊥AD 于点 F.求证:∠BAD=2∠ACF.
C
类型六 倍长中线求角度
6.如图,在△ABC,BA=BC,∠BAC=∠BCA=α,在△CDE中,DC=DE,∠DCE=∠DEC=β,F 是 AE 的中点,连接BF,DF.若 BF⊥DF,且α+2β=130°,则∠ABC 的度数为 .
突破11 构全等(二) 证中点
类型一 找全等,证中点
1.如图,在△ABC 中,∠A=∠ABC,延长 AC 到点 E,过点 E 作EF⊥AB 交AB的延长线于点 F,延长CB 到点 G,过点G 作GH⊥AB 交 AB 的延长线于点 H,且 EF═GH.
(1)求证:△AEF≌△BGH;
(2)连接EG与FH 相交于点D,求证:D 为FH 的中点,且AB=2FD.
类型二 作平行,证中点
2.如图,在△ABC 中,AB=AC,D 为BA 延长线上一点,E 为BC 上一点,DC=DE.
(1)求证:∠BDE=∠ACD;
(2)若DE 是△DBC 的中线,交AC 于点F,求证:DF=EF.
3.如图,在△ABC 中,AB=BC,∠ABC=90°,D 是AC 上一点,AE⊥AC,BD⊥CE,CE交AB 于点F.若AE=AD,求证:F是AB 的中点.
类型三 作垂线,证中点
4.如图,在△ABC 中,AB=AC,∠BAC=90°,D 为AC 上一动点,BD⊥BE,且BD=BE,EC交AB 于点F.求证:F 为EC 的中点.
5.如图,在平面直角坐标系中,A(0,4),C(-2,0),连接AC,过点 A 向右作AD⊥AC,且AD=AC,连接CD.过点M(1,0)作直线MP 垂直于x轴,交CD 于点N,求证:N 为CD 的中点.
6.如图,D 是△ABC 的边BC 的延长线上一点,点 E 在边AC 上,AB=DE,∠BAC=∠DEC.求证:CD=BC.
突破12 构全等(三) 截长补短
类型一 直接截长
1.如图,△DOE 的角平分线DB,EA 相交于点F,∠DOE=60°.求证:DE=DA+EB.
类型二 直接补短
2.如图,在 Rt△ABC 中,∠ABC=90°,以 AC 为边作△ACD,满足 AD=AC,E 为BC 上一点,且 连接DE.求证:DE=CE+2BE.
3.如图,在△ABC中,AB=AC,∠BAC>90°,BD⊥AC,垂足为D,点E在AD上,BE 平分∠ABD,点 F 在BD 延长线上,BF=CE,延长FE 交BC 于点H.
(1)求证:∠CBE=45°;
(2)写出线段 BH 和EH 的位置关系和数量关系,并证明.
4.如图,在△ABC 中,∠BAC=30°,AD 平分∠BAC,点 E 在 BC 的延长线上,∠CAE=75°.若CE=BA+AC,求∠B 的度数.
类型三 间接截长(补短)
5.如图,在四边形 ABDC 中,∠D=∠B=90°,O 为 BD 上的一点,且 AO平分∠BAC,CO平分∠ACD.求证:AB+CD=AC.
6.如图,BN 为∠MBC 的平分线,P 为BN 上一点,且 PD⊥BC 于点 D,∠APC+∠ABC=180°.
(1)求证:PA=PC;
(2)求证:BC-AB=2CD.
C
突破 13 构全等(四) 面积巧转化
类型一 全等割补
1.如图,在四边形ABCD 中,AD∥BC,E 是CD 的中点,EF⊥AB 于点F,AB=10,EF=4,则四边形ABCD 的面积为 .
类型二 全等拼接
2.如图,在 Rt△ABC 中,∠ABC=90°,BD 是△ABC 的角平分线,DE⊥AB 于点E,DF⊥BC 于点F,AD=6,CD=10,则S△ADE+ S△CDF的值为 .
类型三 作高计算
3.如图,在△ABC 中,∠BAC=90°,AB=AC,BD 是△ABC 的角平分线,若BD=8,求△BDC 的面积.
C
类型四 角分垂,出中点
4.如图,在△ABC 中,AD 平分∠BAC,BD⊥AD,连接CD,若 则S△ABC的值为 .
类型五 三垂直,用和差
5.如图,在△ABC 中,AB=AC,∠BAC=90°,M 是△ABC外一点,AM⊥CM,N是BM上一点,AN⊥CN,若AM=10,AN=7,则△AMN的面积为 .
C
类型六 手拉手,构巧图
6.如图,D 为△ABC 内一点,CD⊥BD,CD=BD,∠BAD=45°,AB=12.求
类型七 平行出,等积现
7.如图,在长方形ABCD 中,E,F 分别是边AD,AB 上的点,BE,DF 交于点O,BE=DF,连接OC.求证:OC平分∠BOD.
类型八 构双高,求长度
8.如图,在正方形ABCD 中,E 是正方形内一点,AE⊥BE,连接DE,CF⊥DE 于点 F,EF=2,DF=5.
(1)求△AED 的面积;
(2)求 AE 的长.
突破10 构全等(一) 知中点
1.证明:延长 ED 至点 G,使 DG =DE,连接GC,GF.
∵AD 是BC上的中线,
∴BD=CD.
在△BDE 与△CDG 中,
∴△BDE≌△CDG(SAS),
∴BE=CG.
∵ED⊥FD,
∴∠EDF=∠GDF=90°.
∵DE=DG,DF=DF,
∴△EDF≌△GDF(SAS),
∴EF=FG.
在△FCG 中,
∵GC+FC>FG,
∴BE+FC>EF.
2. B 解:过点 B 作BG⊥l于点G.
∵AE⊥l,
∴∠AED=∠BGD=90°.
∵D是边AB 的中点,
∴AD=BD,
∴△AED≌△BGD(AAS),
∴AE=BG.
∵CF⊥l,BG⊥l,
∴CF≤CM,BG≤BM,
∴AE+CF=BG+CF≤BM+CM,即AE+CF≤BC,
∴当点C,F,G,B共线时,AE+CF有最大值,最大值为 BC 的长.
∵BC=6,
∴AE+CF 的最大值为6.故选 B.
3.解:(1)延长 BC 到点 E,使 CE=BC,连接 PE,过点 E 作 EF⊥x 轴于点F.
∵C 是PA 的中点,
∴PC=AC,
∴△ABC≌△PEC,
∴∠ABC=∠PEC,
∴PE∥AB.
∵EF⊥x轴,
∴PO=EF.
∵∠POD=∠EFB=90°,∠PDO=∠CBA,
∴△POD≌△EFB,
∴PD=BE=2BC;
(2)由(1)得 PE=AB=OF=5-2=3,OD=BF=BO+OF=5+3=8,
∴D(8,0).
4.证明:延长CE 交AB 的延长线于点F.
∵E为AD 的中点,
∴AE=ED.
∵AB∥CD,
∴∠F=∠DCE,∠A=∠D,
∴△AFE≌△DCE,
∴AF=CD,CE=EF,
∴CF=2CE,
BF=AF-AB=CD-AB.
在△BCF 中,BC+BF>CF=2CE,∴BC+CD-AB>2CE.
5.证明:延长 AD 至点 E,使 DE =AD,连接 CE,过点 E 作 EH⊥AC于点 H.
∵AD 是△ABC的中线,
∴CD=BD.
在△CDE 和△BDA 中,
∴△CDE≌△BDA(SAS),
∴CE=AB=2AD=AE,∠BAD=∠AEC.
∵EH⊥AC,
∴∠AHE=∠CHE=90°.
∵CE=AE,HE=HE,
∴Rt△AHE≌△Rt△CHE(HL),
∴∠AEH=∠CEH,
∴∠BAD=∠AEC=2∠AEH.
∵CF⊥AD,
∴∠AFC=∠AHE=90°,
∴∠ACF + ∠CAF = ∠AEH +∠CAF=90°,
∴∠ACF=∠AEH,
∴∠BAD=2∠ACF.
6.80° 解:延长 DF 到点G,使 FG=DF,连接AG,BG,BD,
设∠AGF=x,∠AGB=y.
∵F 是AE 的中点,
∴AF=EF.
∵∠AFG=∠EFD,
∴△AFG≌△EFD(SAS),
∴∠AGF=∠EDF=x,AG=ED.
∵BF⊥DF,
∴BF 是 DG 的垂直平分线,
∴BG=BD,
∴∠BDG = ∠BGD = ∠AGB +∠AGF=x+y.
∵AB=BC,
∴△BAG≌△BCD(SSS),
∴∠AGB=∠CDB=y,∠ABG=∠CBD,
∴∠EDC = ∠EDG + ∠BDG +∠CDB=x+x+y+y=2x+2y.
∵∠ABG=∠CBD,
∴∠ABG + ∠ABD = ∠CBD +∠ABD,
∴∠DBG=∠ABC.
∵ ∠BAC + ∠BCA = 180° ∠ABC,∠BDG+∠BGD=180°—∠DBG,∠BAC=∠BCA=α,
∴∠BAC + ∠BCA = ∠BDG +∠BGD=2α,
∴2(x+y)=2α,
∴x+y=α.
∵∠DCE=∠DEC=β,∠DCE+∠DEC+∠EDC=180°,
∴2β+2x+2y=180°,
∴2β+2α=180°.
∵α+2β=130°,
∴∠BAC=∠BCA=50°,
∴∠ABC=180°—∠BAC-∠BCA=80°.故答案为80°.
突破 11 构全等(二) 证中点
1.证明:(1)∵∠A=∠ABC,∠ABC=∠GBH,
∴∠A=∠GBH.
∵EF⊥AB,GH⊥AB,
∴∠AFE=∠BHG.
∵EF=GH,
∴△AEF≌△BGH(AAS);
(2)∵△AEF≌△BGH,
∴AF=BH,
∴AB=FH.
∵EF⊥AB,GH⊥AB,
∴∠EFD=∠GHD.
∵∠EDF=∠GDH,EF=GH,
∴△EFD≌△GHD(AAS),
∴D为FH的中点,且AB=2FD.
2.证明:(1)∵DC=DE,
∴∠DEC=∠DCE.
∵∠DEC=∠BDE+∠B,∠DCE=∠ACB+∠ACD,
∴ ∠BDE + ∠B = ∠ACB +∠ACD.
∵AB=AC,
∴∠B=∠ACB,
∴∠BDE=∠ACD.
(2)作 EG∥CD 交CA 的延长线于点G, 则 ∠CEG + ∠DCE = 180°,∠FCD=∠G.
∵∠BED+∠DEC=180°,
且∠DCE=∠DEC,
∴∠CEG=∠BED.
∵DE 是△DBC 的中线,
∴CE = BE. 在 △CEG 和△BED
中
∴△CEG≌△BED(ASA),
∴GE=DE,
∴DC = GE. 在△CFD 和△GFE
中,
∴△CFD≌△GFE(AAS),
∴DF=EF.
3.证明:过点 B 作 BH∥AE,交 CE 于点 H.
∵AB=BC,∠ABC=90°,BD⊥CE,
∴∠ABD + ∠CBD = ∠CBD +
∴∠ABD=∠BCH.
∵AE⊥AC,∠BAC=∠ACB=45°,
∴∠EAB=∠BAC=∠ACB=45°.
∵BH∥AE,
∴∠ABH=∠EAB=45°,
∠BAD,
∴△ABD≌△BCH(ASA),
∴BH=AD=AE.
∵∠ABH=∠EAB,∠AFE=∠BFH,
∴△AEF≌△BHF(AAS),
∴AF=BF,
∴F 是 AB 的中点.
4.证明:过点 E 作 EH⊥AB 于点 H.
∵BD⊥BE,
∴∠EBD=∠EHB=∠BAC=90°,
∴∠BEH + ∠EBH = ∠ABD +∠EBH=90°,
∴∠BEH=∠ABD.
又∵BD=BE,
∴△BEH≌∠DBA(AAS),
∴EH=AB=AC,
∴△EFH≌△CFA(AAS),
∴EF=CF,即 F 为EC的中点.
5.证明:过点 D 作 DH⊥y 轴,垂足为H,HD 交MP 于点S.
则∠AHD=90°.
∵A(0,4),C(-2,0),
∴CO=2.
∵AD⊥AC,
∴∠CAD=90°,
∴∠CAO+∠DAH=90°.
又∵∠CAO+∠ACO=90°,
∴∠ACO=∠DAH,
∴△CAO≌△ADH(AAS),
∴HD=AO=4.
∵M(1,0),MP 垂直于x 轴,DH⊥y轴,
∴MO=HS=1,∠NMC=∠NSD=90°,
∴DS=HD-HS=4-1=3,CM=CO+OM=2+1=3,
∴DS=CM,
∴△NSD≌△NMC(AAS),
∴CN=ND,即 N 为CD 的中点.
6.证明:分别过点 B,D 作AC 的垂线,垂足分别为G,F,
∵∠BAC=∠DEC,AB=DE,
∴△ABG≌△EDF,
∴BG=DF,
∵∠DFC=∠BGC=90°,∠DCF=∠BCG,
∴△DCF≌△BCG,
∴CD=BC.
突破 12 构全等(三) 截长补短
1.证明:∵∠DOE=60°,
∴∠ODE+∠OED=120°.
∵ DB, EA 分 别 平 分 ∠ODE,∠OED,
∠ODE)=60°,
∴∠AFD=60°,
∴∠BFE=∠AFD=60°.
在 DE上截取DH=DA,连接 FH,则△DAF≌△DHF(SAS),
∴∠DFA=∠DFH,
∴∠DFH=60°,
∴∠EFH=∠EFB.
∵EF=EF,∠HEF=∠BEF,
∴△HFE≌△BFE(ASA),
∴EH=EB.
∵DE=DH+EH,
∴DE=DA+EB.
2.证明:延长EB 至G,使 BG=BE,连接 AG.
∵∠ABC=90°,
∴∠ABG=90°,
∴△GAB≌△EAB(SAS),
∴AG=AE,
∴∠GAE=∠CAD,
∴∠GAE + ∠EAC = ∠CAD +∠EAC,
∴∠GAC = ∠EAD. 在△GAC 与△EAD中,
∴△GAC≌△EAD(SAS),
∴CG=DE.
∵CG=CE+GE=CE+2BE,
∴DE=CE+2BE.
3.解:(1)∵BD⊥AC 于点D,
∴∠BDC=∠FDC=90°,
∴∠DAB+∠DBA=90°.
∵AB=AC,
∴∠ABC=∠C,
∴ ∠DAB = ∠ABC + ∠C =2∠ABC,
∵BE 平分∠ABD,
∴∠CBE = ∠ABC + ∠ABE =
(2)BH⊥EH,BH=EH.理由如下:延长BA 到点G,使AG=AE,连接 EG.
∵AB=AC,
∴AB+AG=AC+AE,
∴BG=CE.
∵BF=CE,
∴BG=BF.
在△EBG 和△EBF 中,
∴△EBG≌△EBF(SAS),
∴∠G=∠F.
∵∠G=∠AEG,
∴∠DAB=∠G+∠AEG=2∠G,
∴∠G=∠C,
∴∠F=∠C.
∵∠HEC=∠DEF,
∴∠BHE=∠C+∠HEC=∠F+
∴BH⊥EH.
∵∠HEB=∠HBE=45°,
∴BH=EH.
4.解:延长CA 至点O,使AO=AB,连接 OE.
∵∠BAC=30°,∠CAE=75°,
∴∠BAE =∠OAE. 在△AOE 和△ABE 中,
∴△AOE≌△ABE(SAS),
∴∠B=∠O.
∵CE=BA+AC,
∴CE=AO+AC=OC,
∴∠O=∠CEO,
∴∠OCE+∠O+∠OEC=∠B+∠BAC+∠B+∠B=180°,故 ∴∠B=50°.
5.证明:过点 O 作OE⊥AC于点E.
∵∠D=∠B=90°,
∴OB⊥AB,OD⊥CD,
∵ AO 平 分 ∠BAC, CO 平 分∠ACD,
∴OB=OE,OD=OE.
∵OA=OA,OC=OC,
∴Rt△OAB≌Rt△OAE(HL), Rt△OCE≌Rt△OCD(HL),
∴AB=AE,CD=CE,
∴AB+CD=AE+CE=AC.
6.证明:(1)过点 P 作 PK⊥AB,垂足为 K.
∵PK⊥AB,PD⊥BC,∠ABP=∠CBP,
∴PK=PD,
∴Rt△BPK≌Rt△BPD(HL),
∴BK=BD.
∵∠APC+∠ABC=180°,∠ABC+∠KPD=180°,
∴∠KPD=∠APC,
∴∠APK=∠CPD,
∴△PAK≌△PCD(ASA),
∴AK=CD,PA=PC;
(2)∵BK=BD,AK=CD,
∴BC-AB=CD+BD-AB=CD+BK-AB=2CD.
突破 13 构全等(四)面积巧转化
1.40 解:延长 AE 交 BC 的延长线于点 H,连接 BE.
∵E是CD的中点,
∴DE=CE,
∵AD∥BC,
∴∠D=∠DCH,
∵∠AED=∠HEC,
∴△ADE≌△HCE,
∴AE=EH,S四边形ABCD =S△ABH =2S△AEB=AB·EF=40.
2.30 解:在 FB上截取FH=AE,连接 DH.
∵BD 平分∠ABC,DE⊥AB 于点E,DF⊥BC于点F,
∴DE=DF,
∴△ADE≌△HDF,
∴AD=DH=6,
∠ADE=∠HDF,
∴∠HDF+∠CDF=90°,即∠HDC=90°,
3.解:过点 C 作CF⊥BD 交 BD 的延长线于点 E,交BA 的延长线于点F.
∵BD平分∠ABC,
∴∠FBE=∠CBE,
∴△BFE≌△BCE,
∴CE=EF,
∵AB=AC,∠ABD=∠ACF,
∴△ABD≌△ACF,
∴BD=CF=2CE=8,
16.
4.14 解:延长 BD 交AC 的延长线于点E.
∵AD 平分∠BAC,BD⊥AD,
∴△ABD≌△AED,
∴BD=DE,
设
则 =7+x,
∴S△ABE=2S△AED=14+2x,
-2x=14.
5.25.5 解:过点 B 作BE⊥AN 于点E,过点 B 作 BF⊥AM 于点 F,
∵AB=AC,∠BAC=90°,
AN⊥CN,AM⊥CM,
△ABE≌△CAN,
△ABF≌△CAM,
∴BE=AN=7,
∴BF=AM=10,
6.解:过点 D 作DE⊥AD 交AB 于点E,
∵∠BAD=45°,
∴△ADE 为等腰直角三角形,
∴AD=DE,
∵BD=CD,BD⊥CD,
∴△ABD≌△ECD,
∴AB=CE=12,
∠BAD=∠CED=45°,
∴∠AEC=90°,
7.证明:连接 CF,CE,过点 C 分别作CG⊥BE 于点G,CH⊥DF 于点 H,
长方形ABCD,
又∵BE=DF,
∴CG=CH,
∴OC 平分∠BOD.
8.解:(1)过点A 作AH⊥DE 于点H,
∵AD=CD,AD⊥CD,
∴△ADH≌△DCF,
∴AH=DF=5,
(2)过点 D 作 DG⊥AE 于点G,
∵AB=AD,AD⊥AB,
∴△ABE≌△DAG,
∴AE=DG,
