丰县宋楼初级中学苏科版七年级数学下册第十二章证明复习课件(共12张PPT)
文档属性
| 名称 | 丰县宋楼初级中学苏科版七年级数学下册第十二章证明复习课件(共12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 19.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-08 00:00:00 | ||
图片预览


文档简介
课件12张PPT。1.通过具体实例,了解定义、命题、定理、推论的意义.
2.结合具体实例,会区分命题的条件和结论,了解原命题及其
逆命题的概念.
3.了解反例的作用,能举出一个命题的的反例.
4.知道三角形内角和定理,会证明内角和定理.会用已学过的定理和推论进行简单的证明.【学习目标】专题一:命题与互逆命题1.下列语句中哪些是命题,哪些不是,并判断其中命题的真假.(1)在同一平面内,不相交的两条直线是平行线.
(2)数学老师今年30岁.
(3)如果a>b, b>c,那么a >c.
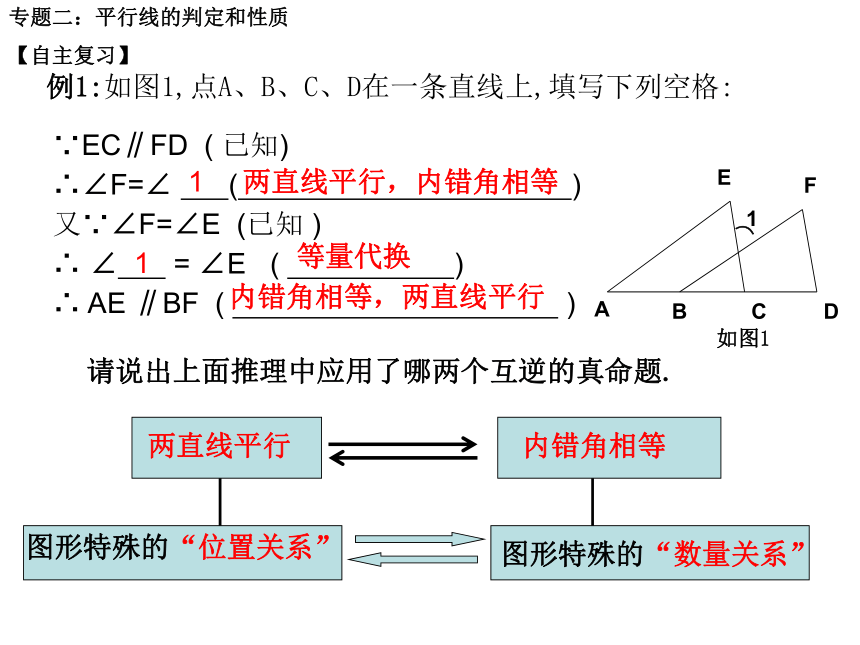
(4)四边形不是多边形.2.指出下列命题的条件和结论,并说出其逆命题.(3)直角三角形的两个锐角互余.是真命题是假命题不是命题(1)如果两个角的补角相等,那么这两个角相等.逆命题:等角的补角相等.(2)对顶角相等.条件:两个角是对顶角.结论:这两个角相等.逆命题:有两个角互余的三角形是直角三角形.逆命题:如果两个角相等,那么这两个角是对顶角.【自主复习】是真命题专题二:平行线的判定和性质例1:如图1,点A、B、C、D在一条直线上,填写下列空格:∵EC∥FD ( 已知)
∴∠F=∠ ( )
又∵∠F=∠E (已知 )
∴ ∠ = ∠E ( )
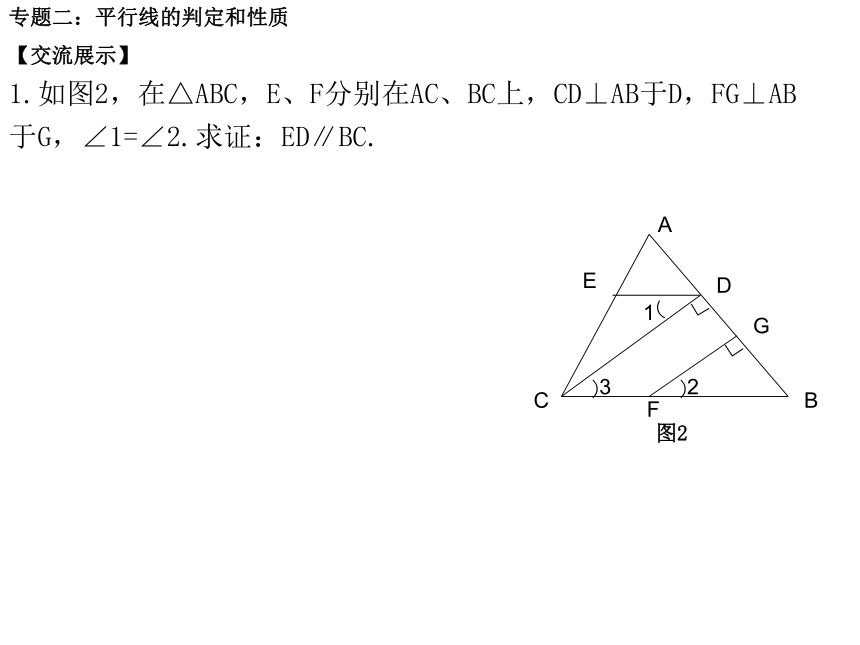
∴ AE ∥BF ( )请说出上面推理中应用了哪两个互逆的真命题.1两直线平行,内错角相等1等量代换内错角相等,两直线平行【自主复习】如图1专题二:平行线的判定和性质1.如图2,在△ABC,E、F分别在AC、BC上,CD⊥AB于D,FG⊥AB于G,∠1=∠2.求证:ED∥BC.【交流展示】图2专题二:平行线的判定和性质【交流展示】
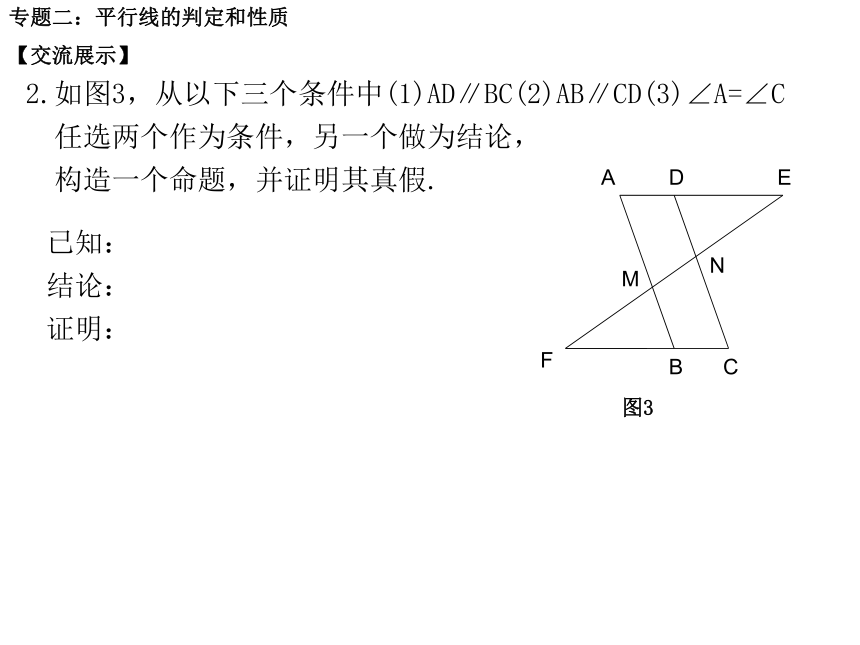
2.如图3,从以下三个条件中(1)AD∥BC(2)AB∥CD(3)∠A=∠C
任选两个作为条件,另一个做为结论,
构造一个命题,并证明其真假.已知:
结论:
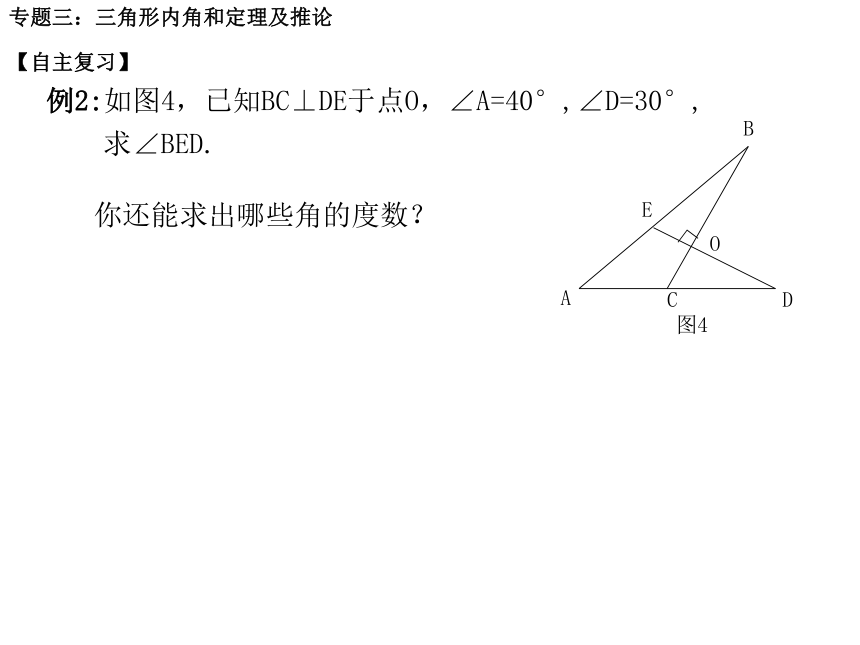
证明: 专题三:三角形内角和定理及推论例2:如图4,已知BC⊥DE于点O,∠A=40°,∠D=30°,
求∠BED.【自主复习】你还能求出哪些角的度数?专题三:三角形内角和定理及推论如图①,若AB∥CD,点P在AB、CD外部时,∠BPD、∠B、∠D有何数量关系? 请证明你的结论.(2)在图① 中,将点P移到AB、CD内部,如图②,题(1)的结 论还是否成立,若不成立,则∠BPD 、∠B、∠D之间有何数量关系?请证明你的结论.图①图②∠B= ∠BPD+ ∠D∠BPD = ∠B + ∠D【交流展示】专题三:三角形内角和定理及推论如图①,若AB∥CD,点P在AB、CD外部时,∠BPD、∠B、∠D有何数量关系? 请证明你的结论.(2)在图① 中,将点P移到AB、CD内部,请画出相应的图形,判断题(1)的结论还是否成立,若不成立,则∠BPD 、∠B、∠D之间有何数量关系?请证明你的结论.图①图②∠B= ∠BPD+ ∠D【交流展示】(3)在图②中,将直线AB绕点B逆时针方向旋转一定角度交 直线CD于点Q 如图③,则∠BPD 、 ∠B、 ∠D、∠BQD 之间 有何数量关系? (4)根据(3)的结论求图④中∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的度数.∠BPD= ∠B+∠D+∠BQD度数之和是360°专题三:三角形内角和定理及推论【交流展示】【走进中考】1.(2014·咸宁)如图,a∥b,等边三角形ABC的顶点B在直线b上,∠1=20°,则∠2的度数为( )
A 60° B 45° C 40° D 30°(第1题)2.(2014 ·衡阳)(1)如图①, ∠1=100°, ∠ C=70 °,则∠ A= .
(2)如图②,将一副三角尺重叠放在一起使直角的顶点重合于点O,
则∠ AOC+ ∠ DOB= .
(3)如图③ ∠ A+∠B+ ∠C+ ∠D+ ∠E+ ∠F= . c30°180°360°ab(2014 徐州七下期末)
14.请写出“内错角相等”的逆命题是 .
24.如图,已知AB∥DE,∠ABC、∠CDE的平分线交于点F,探索 ∠BFE与∠BCE之间的数量关系,并证明你的结论.建议,可否结合P166第13题,看看可否联系起来,变换一下,我好像见过此题!【小结反思】我想对自己说 .
我想对同学说 .
我想对老师说 .
2.结合具体实例,会区分命题的条件和结论,了解原命题及其
逆命题的概念.
3.了解反例的作用,能举出一个命题的的反例.
4.知道三角形内角和定理,会证明内角和定理.会用已学过的定理和推论进行简单的证明.【学习目标】专题一:命题与互逆命题1.下列语句中哪些是命题,哪些不是,并判断其中命题的真假.(1)在同一平面内,不相交的两条直线是平行线.
(2)数学老师今年30岁.
(3)如果a>b, b>c,那么a >c.
(4)四边形不是多边形.2.指出下列命题的条件和结论,并说出其逆命题.(3)直角三角形的两个锐角互余.是真命题是假命题不是命题(1)如果两个角的补角相等,那么这两个角相等.逆命题:等角的补角相等.(2)对顶角相等.条件:两个角是对顶角.结论:这两个角相等.逆命题:有两个角互余的三角形是直角三角形.逆命题:如果两个角相等,那么这两个角是对顶角.【自主复习】是真命题专题二:平行线的判定和性质例1:如图1,点A、B、C、D在一条直线上,填写下列空格:∵EC∥FD ( 已知)
∴∠F=∠ ( )
又∵∠F=∠E (已知 )
∴ ∠ = ∠E ( )
∴ AE ∥BF ( )请说出上面推理中应用了哪两个互逆的真命题.1两直线平行,内错角相等1等量代换内错角相等,两直线平行【自主复习】如图1专题二:平行线的判定和性质1.如图2,在△ABC,E、F分别在AC、BC上,CD⊥AB于D,FG⊥AB于G,∠1=∠2.求证:ED∥BC.【交流展示】图2专题二:平行线的判定和性质【交流展示】
2.如图3,从以下三个条件中(1)AD∥BC(2)AB∥CD(3)∠A=∠C
任选两个作为条件,另一个做为结论,
构造一个命题,并证明其真假.已知:
结论:
证明: 专题三:三角形内角和定理及推论例2:如图4,已知BC⊥DE于点O,∠A=40°,∠D=30°,
求∠BED.【自主复习】你还能求出哪些角的度数?专题三:三角形内角和定理及推论如图①,若AB∥CD,点P在AB、CD外部时,∠BPD、∠B、∠D有何数量关系? 请证明你的结论.(2)在图① 中,将点P移到AB、CD内部,如图②,题(1)的结 论还是否成立,若不成立,则∠BPD 、∠B、∠D之间有何数量关系?请证明你的结论.图①图②∠B= ∠BPD+ ∠D∠BPD = ∠B + ∠D【交流展示】专题三:三角形内角和定理及推论如图①,若AB∥CD,点P在AB、CD外部时,∠BPD、∠B、∠D有何数量关系? 请证明你的结论.(2)在图① 中,将点P移到AB、CD内部,请画出相应的图形,判断题(1)的结论还是否成立,若不成立,则∠BPD 、∠B、∠D之间有何数量关系?请证明你的结论.图①图②∠B= ∠BPD+ ∠D【交流展示】(3)在图②中,将直线AB绕点B逆时针方向旋转一定角度交 直线CD于点Q 如图③,则∠BPD 、 ∠B、 ∠D、∠BQD 之间 有何数量关系? (4)根据(3)的结论求图④中∠A+ ∠B+ ∠C+ ∠D+ ∠E+ ∠F的度数.∠BPD= ∠B+∠D+∠BQD度数之和是360°专题三:三角形内角和定理及推论【交流展示】【走进中考】1.(2014·咸宁)如图,a∥b,等边三角形ABC的顶点B在直线b上,∠1=20°,则∠2的度数为( )
A 60° B 45° C 40° D 30°(第1题)2.(2014 ·衡阳)(1)如图①, ∠1=100°, ∠ C=70 °,则∠ A= .
(2)如图②,将一副三角尺重叠放在一起使直角的顶点重合于点O,
则∠ AOC+ ∠ DOB= .
(3)如图③ ∠ A+∠B+ ∠C+ ∠D+ ∠E+ ∠F= . c30°180°360°ab(2014 徐州七下期末)
14.请写出“内错角相等”的逆命题是 .
24.如图,已知AB∥DE,∠ABC、∠CDE的平分线交于点F,探索 ∠BFE与∠BCE之间的数量关系,并证明你的结论.建议,可否结合P166第13题,看看可否联系起来,变换一下,我好像见过此题!【小结反思】我想对自己说 .
我想对同学说 .
我想对老师说 .
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
