迁安市迁安镇丁官营初级中学冀教版七年级数学下册7.5平行线的性质课件(共21张PPT)
文档属性
| 名称 | 迁安市迁安镇丁官营初级中学冀教版七年级数学下册7.5平行线的性质课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-08 11:21:09 | ||
图片预览


文档简介
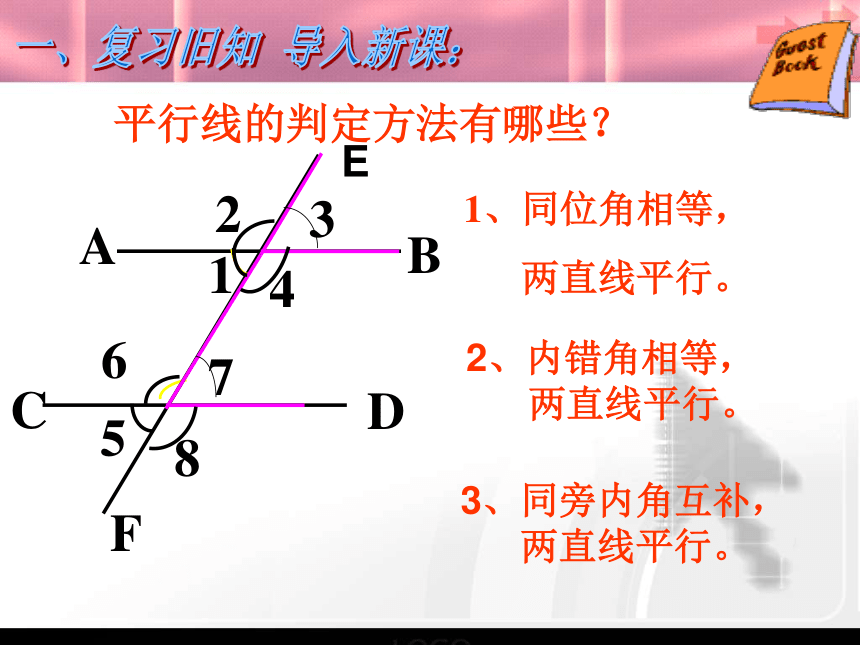
课件21张PPT。迁安镇丁官营中学 王翠霞7.5 平行线的性质平行线的判定方法有哪些?1、同位角相等,
两直线平行。1、同位角相等,
两直线平行。CDABF85612347一、复习旧知 导入新课:2、内错角相等,
两直线平行。3、同旁内角互补,
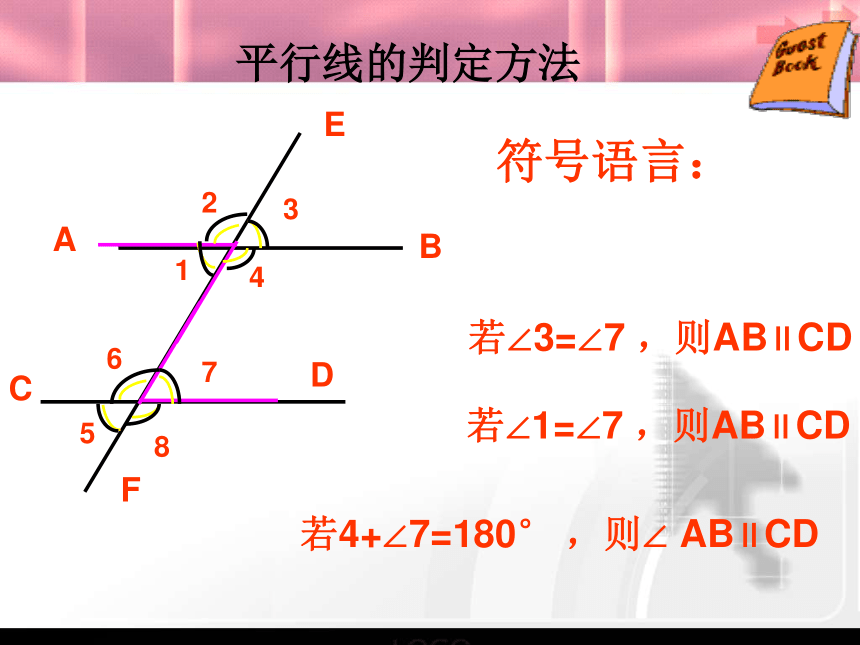
两直线平行。E平行线的判定方法ABEFCD12345678若∠1=∠7 ,则AB∥CD若∠3=∠7 ,则AB∥CD符号语言:
若4+∠7=180° ,则∠ AB∥CD探究一若直线AB∥CD,
你知道同位角有什
么关系吗?若直线AB∥CD,
你知道同位角有什
么关系吗?若直线AB∥CD,
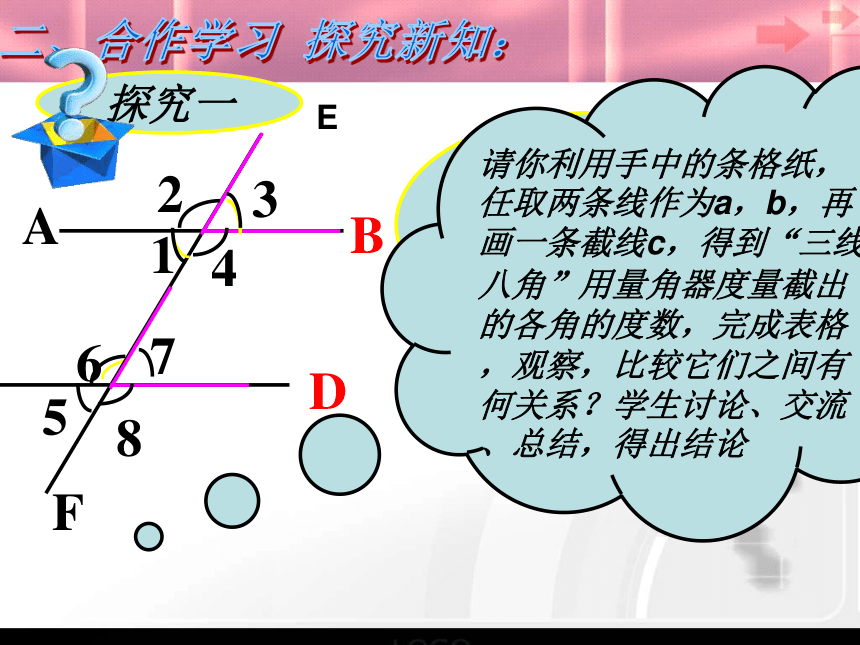
是否有同位角相等呢?你有什么办法来说明?二、合作学习 探究新知:请你利用手中的条格纸,任取两条线作为a,b,再画一条截线c,得到“三线八角”用量角器度量截出的各角的度数,完成表格,观察,比较它们之间有何关系?学生讨论、交流、总结,得出结论
E完成下列表格平行线的性质符号语言:
若AB ∥ CD,
则
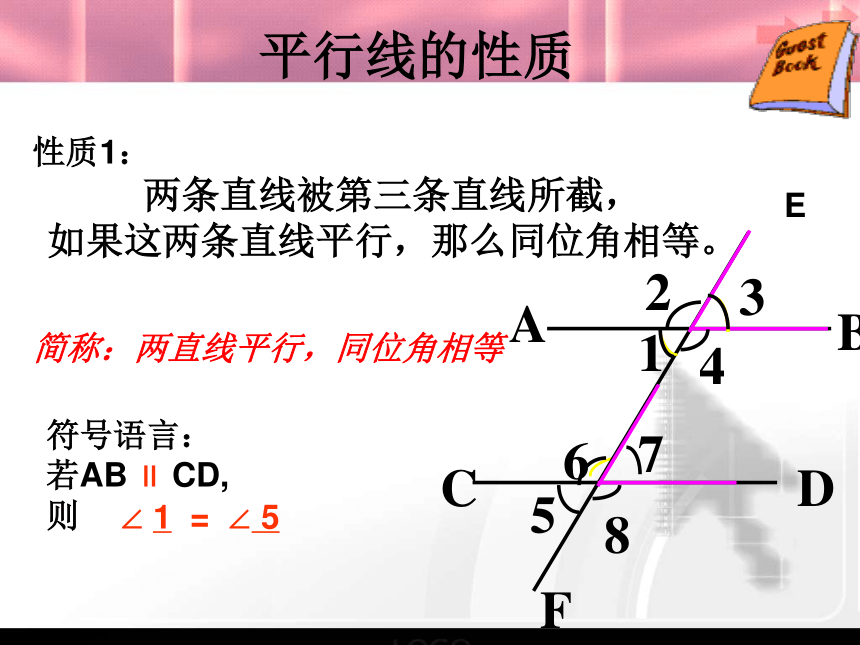
性质1:
两条直线被第三条直线所截,
如果这两条直线平行,那么同位角相等。
∠ 1 = ∠ 5
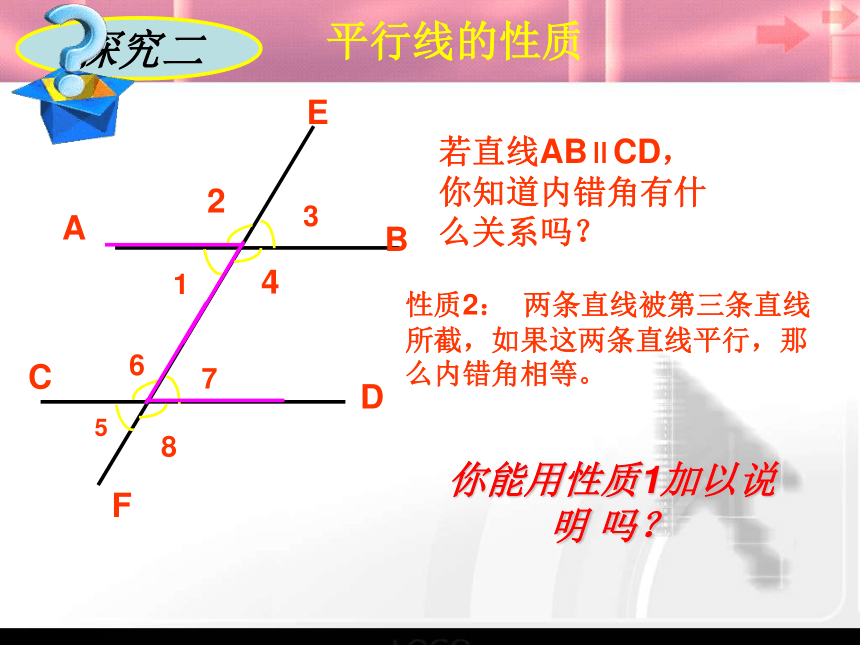
简称:两直线平行,同位角相等E探究二ABCDEF12346857平行线的性质若直线AB∥CD,
你知道内错角有什
么关系吗?你能用性质1加以说
明 吗?性质2: 两条直线被第三条直线 所截,如果这两条直线平行,那么内错角相等。
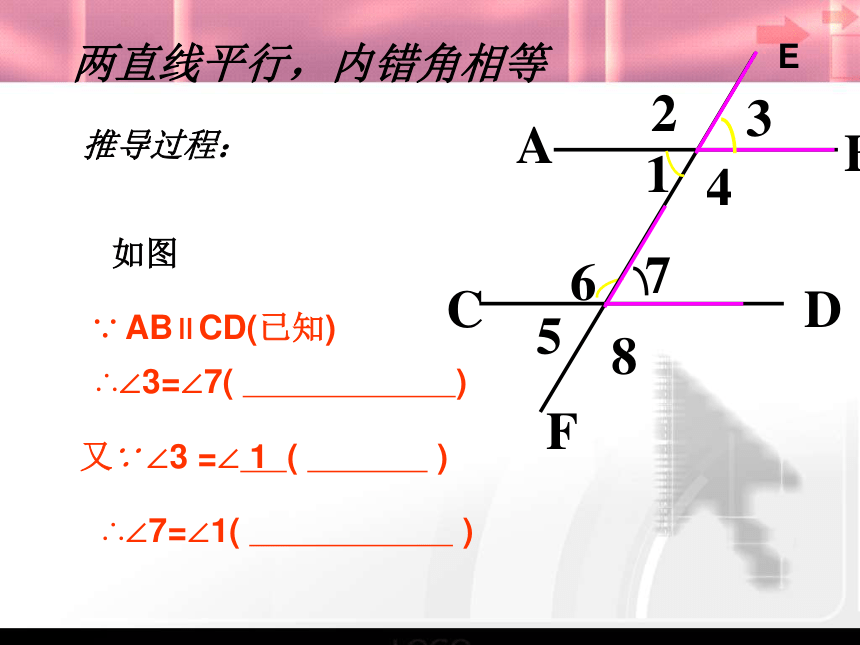
如图∴∠3=∠7( )∵ AB∥CD(已知)又∵ ∠3 =∠ 1 ( )∴∠7=∠1( )
E两直线平行,内错角相等推导过程:平行线的性质若直线AB∥CD,
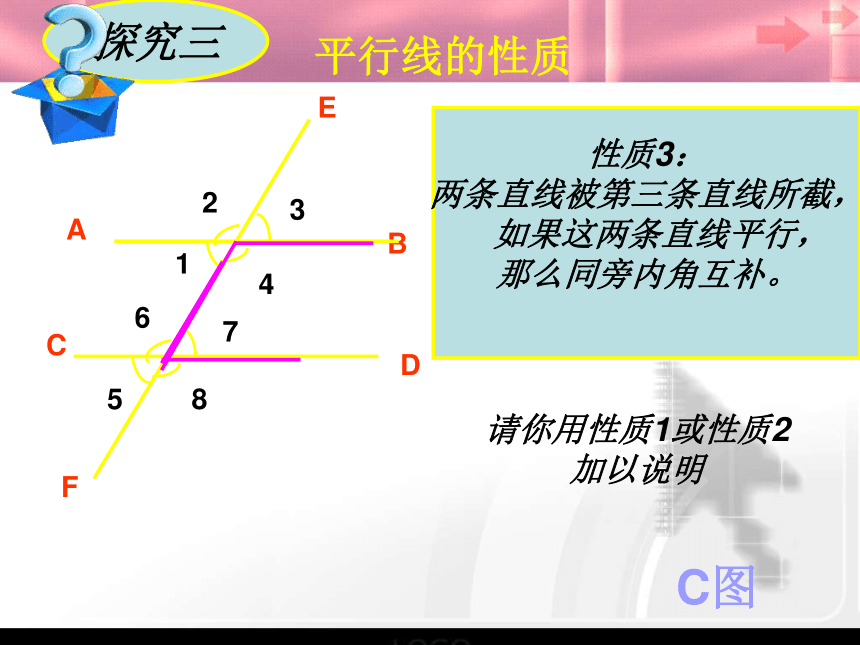
你知道同旁内角
有什么关系吗?C图 若直线AB∥CD,
你知道同旁内角
有什么关系吗?性质3:
两条直线被第三条直线所截,
如果这两条直线平行,
那么同旁内角互补。
请你用性质1或性质2加以说明探究三如图
∵ AB∥CD(已知)
∴∠3=∠7( )
又∵ ∠3 + ∠ 4= 180° ( )
∴∠7+∠4 = 180 ° ( )两直线平行,同旁内角互补推导过程:平行线的性质两直线平行,同位角相等符号语言:若a∥b,则∠3=∠2两直线平行, 内错角相等符号语言:若a∥b,则∠1=∠2两直线平行,同旁内角互补 符号语言:若a∥b,则∠ 4+∠2=180°总结平行线的性质抢答:如图已知直线a、b被直线c所截,在括号内为下面的推理填上适当的根据:(1)∵ a∥b,∴∠3=∠1( )
(2)∵ ∠3=∠1,∴ a∥b ( )
(3) ∵ a∥b,∴∠2=∠1( )
(4) ∵ a∥b, ∴∠1 + ∠ 4= 180° ( )
(5) ∵ ∠1=∠2,∴ a∥b ( )
(6)∠1 + ∠ 4= 180 ° ∴ a∥b ( )c11、如图直线a∥b ,∠1=70°,则∠2=_____2、如图AB∥D C,则______,理由是:_________;
AD∥BC, 则__________,理由:________。
(2题图)(1题图)ABCD21基础练习(一)70°∠1= ∠3∠2= ∠43、如图,若∠1=∠B,则___∥____,∠2+∠C=____4、如图,梯形ABCD中,AD∥BC, ∠B=70°,∠D=135° ,
则∠A=____,∠C=____
ADBC(3题图)(4题图)2基础练习(二)DEBC180°110°45°1、如图,直线 a∥b ,c ∥ d,∠1=73°
求∠ 2、 ∠ 3各是多少度?∵ a∥b (已知)
∴∠1=∠4 ( )
∠2+∠ 3=180°( )
又∵ ∠1 =54°( 已知 )
∴∠4=∠54°( )
∴∠2=∠1=∠54°
∴∠ 3=180°-54°=126°∵ a∥b (已知)
∴∠1=∠4 ( )
∠2+∠ 3=180°( )
又∵ ∠1 =54°( 已知 )
∴∠4=∠54°( )
∴∠2=∠1=∠54°
∴∠ 3=180°-54°=126°∵ a∥b (已知)
∴∠1=∠2 ( )
∵ ∠1 =73°( )
∴ ∠2=73°( )
又∵ c ∥ d (已知 )
∴∠1+ ∠ 3 =180°( )
∴∠3=180°-∠1 ( )
∴∠ 3=180°-73°=107°三、运用新知 尝试推理:结合条件认真读图,会从图中提取相关信息,结合已知条件,得出结论,进行推理 如图:AB∥D C,AD∥BC,∠1=100,
求 ∠2,∠D 的度数?因为AB∥D C 所以∠1+∠D=180°( )因为∠1=100°所以∠D=180°-100°=80°因为AD∥B C所以∠1=∠2 ( )因为∠1=100°所以∠2=100°四、巩固新知 体验成功:
如图,AB∥EF, CD∥EF ,∠B=40°、∠D=35 °,
求∠BED的大小。
提高练习类比“平行线的判定”与“平行线的性质”判定性质1、同位角相等,
两直线平行1、两直线平行,
同位角相等2、两直线平行,
内错角相等2、内错角相等,
两直线平行3、同旁内角互补,两直线平行3、两直线平行,
同旁内角互补五、课堂交流 总结提升:类比由角的大小关系转化为直线的位置关系平行线的
判定平行线的
性质由直线的位置关系转化为角的大小关系1、本节课你学到了什么知识?平行线的性质2、你还学到了什么数学思想?转化的数学思想帮助学生形成知识体系,使学生对本节课所学的知识有一个系统的认识。布置作业:课本第 51 页
第1题、2题六、小结与作业努力现在,成就未来再见
两直线平行。1、同位角相等,
两直线平行。CDABF85612347一、复习旧知 导入新课:2、内错角相等,
两直线平行。3、同旁内角互补,
两直线平行。E平行线的判定方法ABEFCD12345678若∠1=∠7 ,则AB∥CD若∠3=∠7 ,则AB∥CD符号语言:
若4+∠7=180° ,则∠ AB∥CD探究一若直线AB∥CD,
你知道同位角有什
么关系吗?若直线AB∥CD,
你知道同位角有什
么关系吗?若直线AB∥CD,
是否有同位角相等呢?你有什么办法来说明?二、合作学习 探究新知:请你利用手中的条格纸,任取两条线作为a,b,再画一条截线c,得到“三线八角”用量角器度量截出的各角的度数,完成表格,观察,比较它们之间有何关系?学生讨论、交流、总结,得出结论
E完成下列表格平行线的性质符号语言:
若AB ∥ CD,
则
性质1:
两条直线被第三条直线所截,
如果这两条直线平行,那么同位角相等。
∠ 1 = ∠ 5
简称:两直线平行,同位角相等E探究二ABCDEF12346857平行线的性质若直线AB∥CD,
你知道内错角有什
么关系吗?你能用性质1加以说
明 吗?性质2: 两条直线被第三条直线 所截,如果这两条直线平行,那么内错角相等。
如图∴∠3=∠7( )∵ AB∥CD(已知)又∵ ∠3 =∠ 1 ( )∴∠7=∠1( )
E两直线平行,内错角相等推导过程:平行线的性质若直线AB∥CD,
你知道同旁内角
有什么关系吗?C图 若直线AB∥CD,
你知道同旁内角
有什么关系吗?性质3:
两条直线被第三条直线所截,
如果这两条直线平行,
那么同旁内角互补。
请你用性质1或性质2加以说明探究三如图
∵ AB∥CD(已知)
∴∠3=∠7( )
又∵ ∠3 + ∠ 4= 180° ( )
∴∠7+∠4 = 180 ° ( )两直线平行,同旁内角互补推导过程:平行线的性质两直线平行,同位角相等符号语言:若a∥b,则∠3=∠2两直线平行, 内错角相等符号语言:若a∥b,则∠1=∠2两直线平行,同旁内角互补 符号语言:若a∥b,则∠ 4+∠2=180°总结平行线的性质抢答:如图已知直线a、b被直线c所截,在括号内为下面的推理填上适当的根据:(1)∵ a∥b,∴∠3=∠1( )
(2)∵ ∠3=∠1,∴ a∥b ( )
(3) ∵ a∥b,∴∠2=∠1( )
(4) ∵ a∥b, ∴∠1 + ∠ 4= 180° ( )
(5) ∵ ∠1=∠2,∴ a∥b ( )
(6)∠1 + ∠ 4= 180 ° ∴ a∥b ( )c11、如图直线a∥b ,∠1=70°,则∠2=_____2、如图AB∥D C,则______,理由是:_________;
AD∥BC, 则__________,理由:________。
(2题图)(1题图)ABCD21基础练习(一)70°∠1= ∠3∠2= ∠43、如图,若∠1=∠B,则___∥____,∠2+∠C=____4、如图,梯形ABCD中,AD∥BC, ∠B=70°,∠D=135° ,
则∠A=____,∠C=____
ADBC(3题图)(4题图)2基础练习(二)DEBC180°110°45°1、如图,直线 a∥b ,c ∥ d,∠1=73°
求∠ 2、 ∠ 3各是多少度?∵ a∥b (已知)
∴∠1=∠4 ( )
∠2+∠ 3=180°( )
又∵ ∠1 =54°( 已知 )
∴∠4=∠54°( )
∴∠2=∠1=∠54°
∴∠ 3=180°-54°=126°∵ a∥b (已知)
∴∠1=∠4 ( )
∠2+∠ 3=180°( )
又∵ ∠1 =54°( 已知 )
∴∠4=∠54°( )
∴∠2=∠1=∠54°
∴∠ 3=180°-54°=126°∵ a∥b (已知)
∴∠1=∠2 ( )
∵ ∠1 =73°( )
∴ ∠2=73°( )
又∵ c ∥ d (已知 )
∴∠1+ ∠ 3 =180°( )
∴∠3=180°-∠1 ( )
∴∠ 3=180°-73°=107°三、运用新知 尝试推理:结合条件认真读图,会从图中提取相关信息,结合已知条件,得出结论,进行推理 如图:AB∥D C,AD∥BC,∠1=100,
求 ∠2,∠D 的度数?因为AB∥D C 所以∠1+∠D=180°( )因为∠1=100°所以∠D=180°-100°=80°因为AD∥B C所以∠1=∠2 ( )因为∠1=100°所以∠2=100°四、巩固新知 体验成功:
如图,AB∥EF, CD∥EF ,∠B=40°、∠D=35 °,
求∠BED的大小。
提高练习类比“平行线的判定”与“平行线的性质”判定性质1、同位角相等,
两直线平行1、两直线平行,
同位角相等2、两直线平行,
内错角相等2、内错角相等,
两直线平行3、同旁内角互补,两直线平行3、两直线平行,
同旁内角互补五、课堂交流 总结提升:类比由角的大小关系转化为直线的位置关系平行线的
判定平行线的
性质由直线的位置关系转化为角的大小关系1、本节课你学到了什么知识?平行线的性质2、你还学到了什么数学思想?转化的数学思想帮助学生形成知识体系,使学生对本节课所学的知识有一个系统的认识。布置作业:课本第 51 页
第1题、2题六、小结与作业努力现在,成就未来再见
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
