青龙满族自治县凉水河初级中学冀教版七年级数学下册7.2相交线第一课时课件(共21张PPT)
文档属性
| 名称 | 青龙满族自治县凉水河初级中学冀教版七年级数学下册7.2相交线第一课时课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-08 09:49:30 | ||
图片预览


文档简介
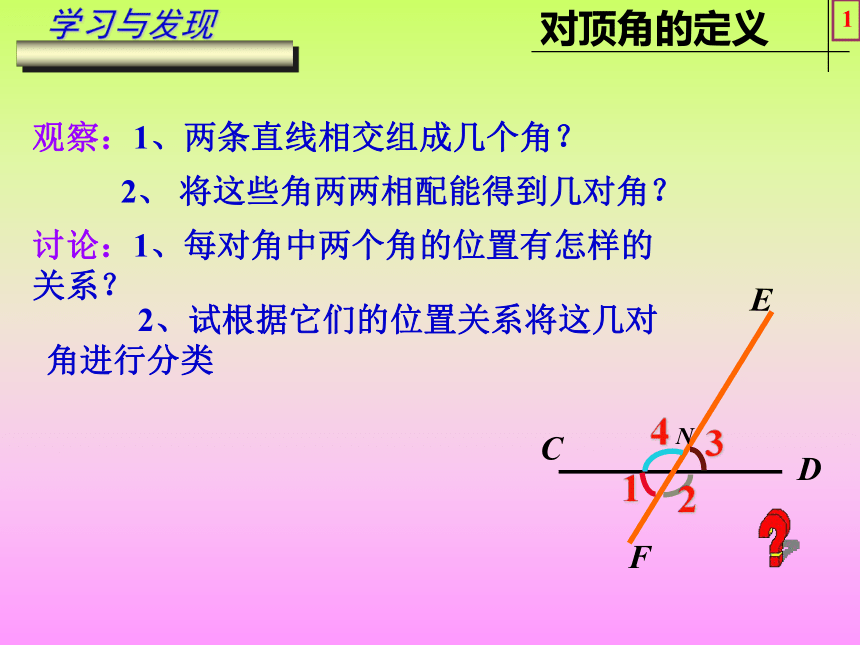
课件21张PPT。7.2 相交线凉水河中学 杜海姣冀教版七年级下册(第一课时) 为了测量纸杯的侧壁交角,聪明的小红设计了如下的方案,你能说明其中的原理吗?情境引入CDEFN学习与发现1观察:1、两条直线相交组成几个角?2、 将这些角两两相配能得到几对角?讨论:1、每对角中两个角的位置有怎样的关系? 2、试根据它们的位置关系将这几对 角进行分类CDEF这样两个角之间的关系叫邻补角N像这样的两个角顶点什么关系?
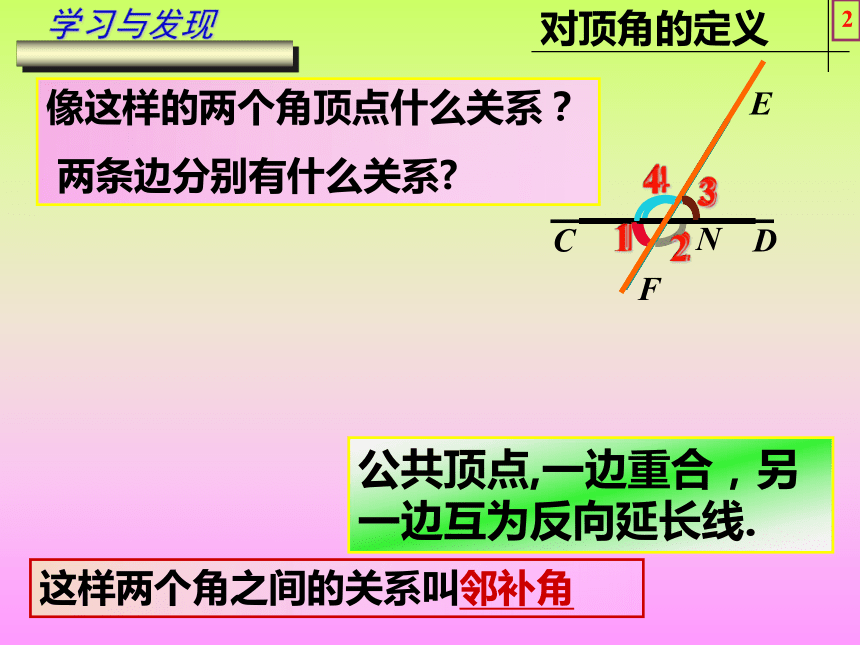
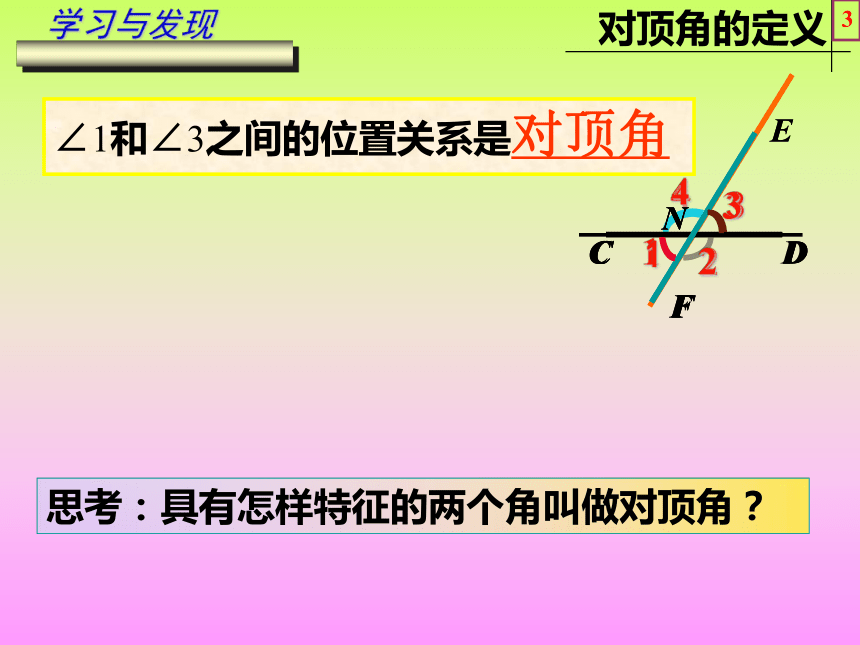
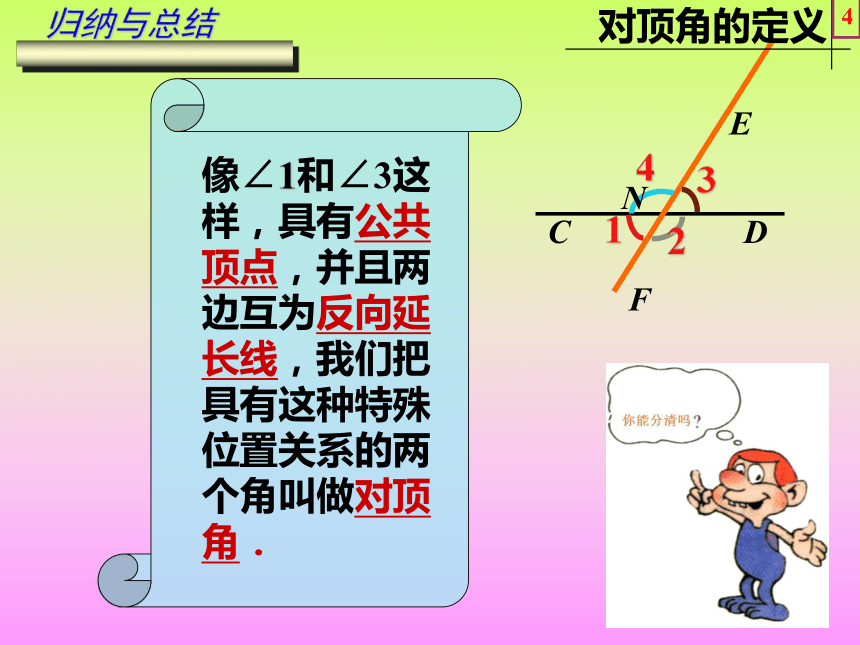
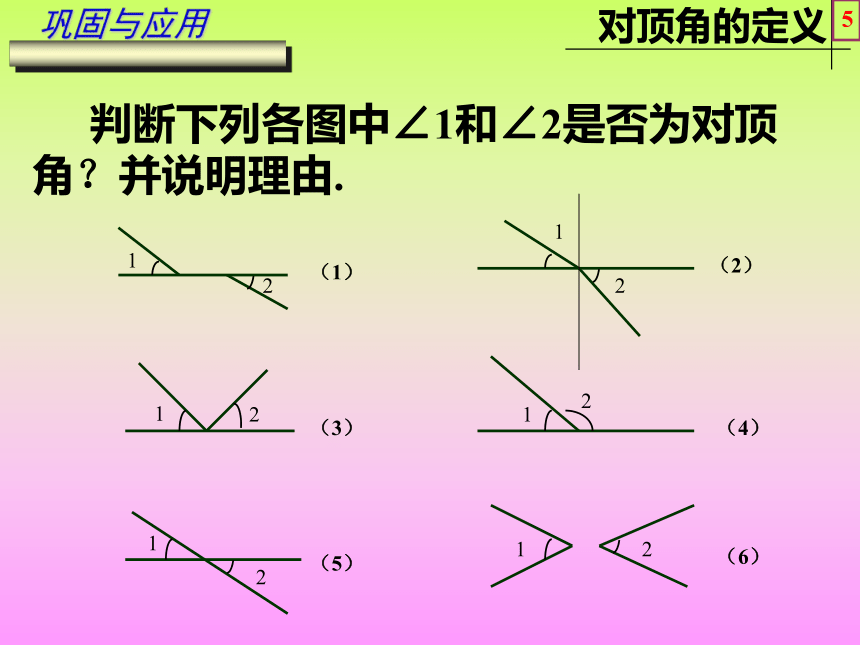
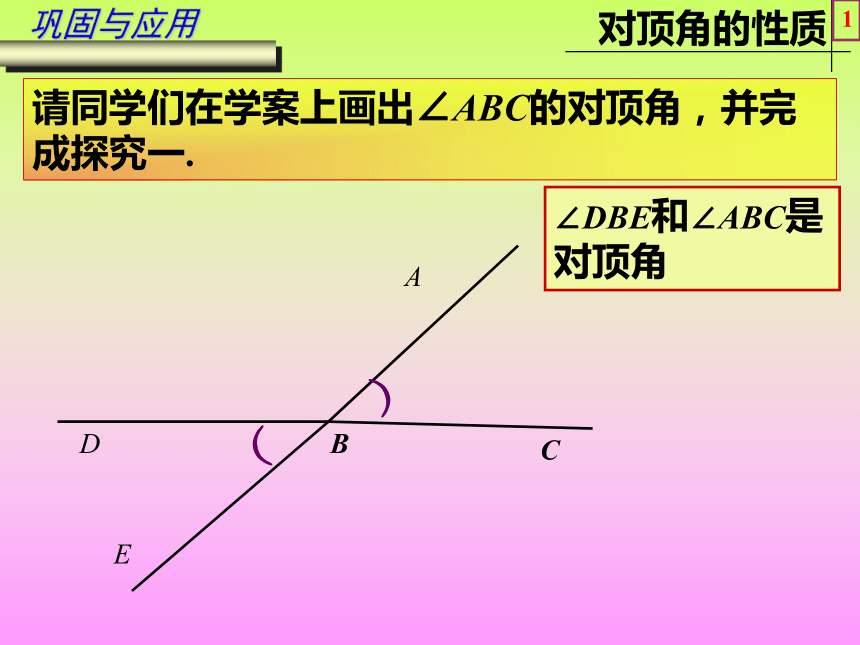
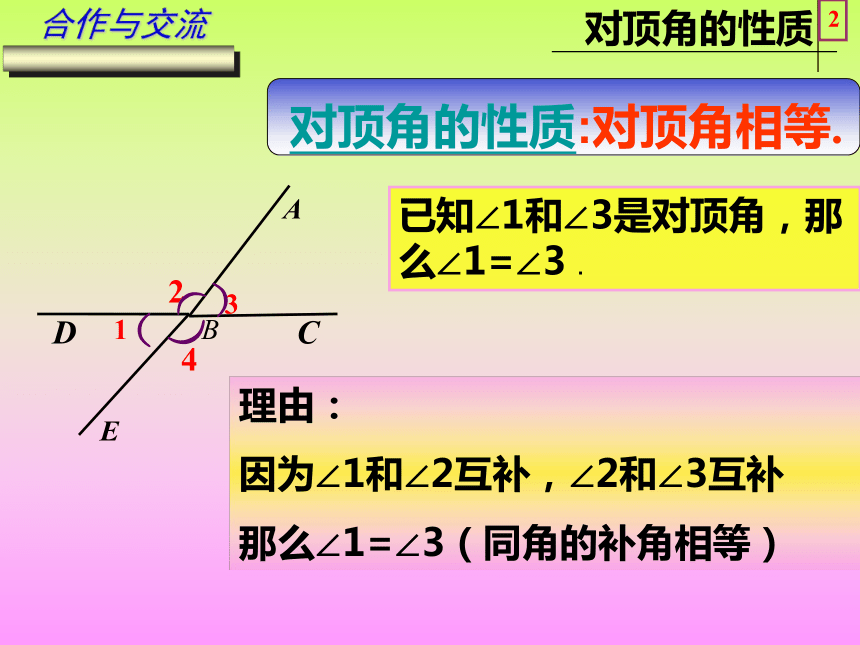
两条边分别有什么关系?公共顶点,一边重合,另一边互为反向延长线.学习与发现2EDCF∠1和∠3之间的位置关系是对顶角思考:具有怎样特征的两个角叫做对顶角?N学习与发现3CFDCFNDCFENDCF像∠1和∠3这样,具有公共顶点,并且两边互为反向延长线,我们把具有这种特殊位置关系的两个角叫做对顶角.归纳与总结4EDNCF 判断下列各图中∠1和∠2是否为对顶角?并说明理由.121212121212(1)(2)(3)(4)(5)(6)巩固与应用5ABC请同学们在学案上画出∠ABC的对顶角,并完成探究一.DE∠DBE和∠ABC是对顶角巩固与应用1))ABDE(1342)((已知∠1和∠3是对顶角,那么∠1=∠3 .理由:
因为∠1和∠2互补,∠2和∠3互补
那么∠1=∠3(同角的补角相等)C合作与交流2对顶角的性质:对顶角相等.4132ADCBFE截线 直线AB和CD被直线EF所截.NM学习与发现1如图:直线 ____和直线____被直线_____所截,形成____个角,简称为________.
其中对顶角有___
对,它们分别是_____________BDF三线八角CDEF8AB4如图,直线 l 截a、b于点P、Qlab12345867PQ∠1和∠5都在被截直线a、b的上方,截线l的右边∠2和∠6
∠3和∠7
∠4和∠8相交线中的角 从位置方面观察
∠1与∠5有什么特征.
∠1与∠5这样位置的一对角是同位角.1、同位角如图,直线 l 截a、b于点P、Qlab12345867PQ∠3和∠5都在被截直线a、b的内侧,分别截线l的两旁内错角:∠3和∠5∠4和∠6 从位置方面观察
∠3与∠5有什么特征.
2、内错角如图,直线 l 截a、b于点P、Qlab12345867PQ∠4和∠5都在被截直线a、b的内侧,截线l的同旁同旁内角:∠4和∠5 ∠3和∠6 从位置方面观察
∠4与∠5有什么特征.
3、同旁内角如图:直线a、b被直线 l 截的8个角中 同位角:∠1与∠5;
∠2与∠6;
∠4与∠8;
∠3与∠7. 内错角:∠3与∠5;
∠4与∠6.同旁内角: ∠4与∠5; ∠3与∠6.练习: 1.下列各图中的∠1与∠2是不是同位角?不是注意:有两条直线被第三条直线所
截的条件时才能产生同位
角、内错角、同旁内角.是不是谈谈你的收获1、若∠1与∠2是对顶角,∠1=160,则∠2=______。
1802、若∠1与∠2为对顶角,∠1与∠3互补,则 ∠2+∠3= 0163、图中是对顶角量角器,你能说出用它测量角的原理吗?答:对顶角相等。巩固与应用4.右图中∠1的同位角有( )
∠1的内错角有( )
∠1的同旁内角有( )
巩固与应用5.上题中∠2=110°,求∠8和∠4
的度数.∠3,∠2∠4,∠5∠8,∠9指出右图中的同位角、 内错角、同旁内角.6.作业1.必做题:课本P37—P38习题.
2.选做题:如图,直线AB、CD交EF 于点G、H,∠2=∠3,∠1=70°,求∠4的度数.AHCBDEFG1234谢谢,再见
两条边分别有什么关系?公共顶点,一边重合,另一边互为反向延长线.学习与发现2EDCF∠1和∠3之间的位置关系是对顶角思考:具有怎样特征的两个角叫做对顶角?N学习与发现3CFDCFNDCFENDCF像∠1和∠3这样,具有公共顶点,并且两边互为反向延长线,我们把具有这种特殊位置关系的两个角叫做对顶角.归纳与总结4EDNCF 判断下列各图中∠1和∠2是否为对顶角?并说明理由.121212121212(1)(2)(3)(4)(5)(6)巩固与应用5ABC请同学们在学案上画出∠ABC的对顶角,并完成探究一.DE∠DBE和∠ABC是对顶角巩固与应用1))ABDE(1342)((已知∠1和∠3是对顶角,那么∠1=∠3 .理由:
因为∠1和∠2互补,∠2和∠3互补
那么∠1=∠3(同角的补角相等)C合作与交流2对顶角的性质:对顶角相等.4132ADCBFE截线 直线AB和CD被直线EF所截.NM学习与发现1如图:直线 ____和直线____被直线_____所截,形成____个角,简称为________.
其中对顶角有___
对,它们分别是_____________BDF三线八角CDEF8AB4如图,直线 l 截a、b于点P、Qlab12345867PQ∠1和∠5都在被截直线a、b的上方,截线l的右边∠2和∠6
∠3和∠7
∠4和∠8相交线中的角 从位置方面观察
∠1与∠5有什么特征.
∠1与∠5这样位置的一对角是同位角.1、同位角如图,直线 l 截a、b于点P、Qlab12345867PQ∠3和∠5都在被截直线a、b的内侧,分别截线l的两旁内错角:∠3和∠5∠4和∠6 从位置方面观察
∠3与∠5有什么特征.
2、内错角如图,直线 l 截a、b于点P、Qlab12345867PQ∠4和∠5都在被截直线a、b的内侧,截线l的同旁同旁内角:∠4和∠5 ∠3和∠6 从位置方面观察
∠4与∠5有什么特征.
3、同旁内角如图:直线a、b被直线 l 截的8个角中 同位角:∠1与∠5;
∠2与∠6;
∠4与∠8;
∠3与∠7. 内错角:∠3与∠5;
∠4与∠6.同旁内角: ∠4与∠5; ∠3与∠6.练习: 1.下列各图中的∠1与∠2是不是同位角?不是注意:有两条直线被第三条直线所
截的条件时才能产生同位
角、内错角、同旁内角.是不是谈谈你的收获1、若∠1与∠2是对顶角,∠1=160,则∠2=______。
1802、若∠1与∠2为对顶角,∠1与∠3互补,则 ∠2+∠3= 0163、图中是对顶角量角器,你能说出用它测量角的原理吗?答:对顶角相等。巩固与应用4.右图中∠1的同位角有( )
∠1的内错角有( )
∠1的同旁内角有( )
巩固与应用5.上题中∠2=110°,求∠8和∠4
的度数.∠3,∠2∠4,∠5∠8,∠9指出右图中的同位角、 内错角、同旁内角.6.作业1.必做题:课本P37—P38习题.
2.选做题:如图,直线AB、CD交EF 于点G、H,∠2=∠3,∠1=70°,求∠4的度数.AHCBDEFG1234谢谢,再见
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
