邢台市第八中学冀教版七年级数学下册8.5 乘法公式课件(共12张PPT)
文档属性
| 名称 | 邢台市第八中学冀教版七年级数学下册8.5 乘法公式课件(共12张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 36.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-08 00:00:00 | ||
图片预览





文档简介
课件12张PPT。8.5 乘法公式平方差公式一起探究(1)(a+b)(a-b) = a2-b2
(2)(x+3)(x-3)= x2-32
(3)(2a+3b)(2a-3b)= (2a)2-(3b)2
(4)(5m+2n)(5m-2n)= (5m)2-(2n)2
平方差公式
(a+b)(a-b)= a2-b2
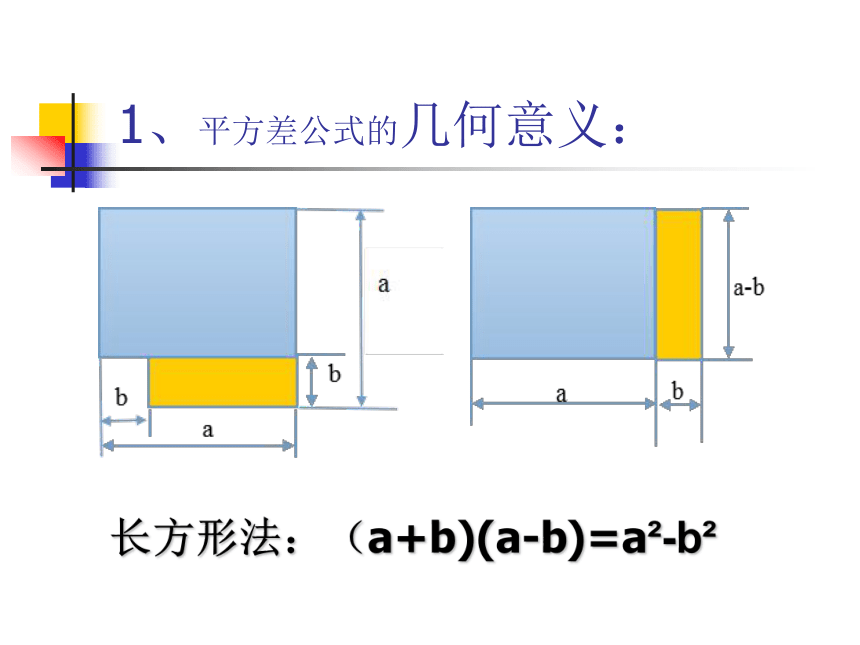
两个数的和与这两个数的差的积,等于这两个数的平方差。1、平方差公式的几何意义:长方形法:(a+b)(a-b)=a2-b2 平方差公式的几何意义:梯形法:(2a+2b)(a-b)=a2-b22、平方差公式的特征:(a+b)(a-b)=a2-b2
公式的左边:一个数不变,也就是a;另一个数是互为相反数,也就是b.
公式的右边:不变那个数的平方,减去互为相反的那个数的平方。即a2-b2 。
所以,在应用平方差公式进行乘法运算时,一定要注意是否符合公式特征?如果满足公式,结果为不变那个数的平方减去变了那个数的平方,一定不要搞了。3、平方差公式的变式:根据不变那个数——a的位置,归纳出平方差公式的变式有四类八种:前头型、后头型、中间型、两头型。其中每一类都有正负两种。
前头型:(a+b)(a-b) =a2-b2 (-a+b)(-a-b) = (-a)2-b2
后头型:(b+a)(-b+a) = a2-b2 (b-a)(-b-a) =(-a)2-b2
中间型:(b+a)(a-b) = a2-b2 (b-a)(-a-b) =(-a)2-b2
两头型:(a+b)(-b+a) = a2-b2 (-a+b)(-b-a)=(-a)2-b2
4、平方差公式的作用:若两个二项式相乘满足平方差公式时,则可以直接写出结果。省去中间的各式相乘以及合并同类项,既快捷又准确。例题:(1)(2x-y)(2x+y)
(2)(3m-5n)(-5n-3m)
(3)(6-2b)(2b+6)
(4)(-3m-4n)(3m-4n)课堂练习:(1)(-m+n)(-m-n)
(2)(2a+5b)(-2a+5b)
(3)(5m-2)(-5m-2)
(4)(2x+3y)(3y-2x)
(5)(3a-5b)(5b+3a)
(6)(a+b+c)(a+b-c)课堂小结:1、是重要平方差公式的乘法公式之一。
2、它的作用在于:当两个二项式相乘符合平方差公式时,可以利用公式直接求出结果,既快捷又准确。
3、判断是否满足公式的条件是应用公式的前提。掌握公式的条件和四种变式是灵活运用平分差公式的基础。课外作业:P88页,习题A组、B组。
预习完全平方公式。
(2)(x+3)(x-3)= x2-32
(3)(2a+3b)(2a-3b)= (2a)2-(3b)2
(4)(5m+2n)(5m-2n)= (5m)2-(2n)2
平方差公式
(a+b)(a-b)= a2-b2
两个数的和与这两个数的差的积,等于这两个数的平方差。1、平方差公式的几何意义:长方形法:(a+b)(a-b)=a2-b2 平方差公式的几何意义:梯形法:(2a+2b)(a-b)=a2-b22、平方差公式的特征:(a+b)(a-b)=a2-b2
公式的左边:一个数不变,也就是a;另一个数是互为相反数,也就是b.
公式的右边:不变那个数的平方,减去互为相反的那个数的平方。即a2-b2 。
所以,在应用平方差公式进行乘法运算时,一定要注意是否符合公式特征?如果满足公式,结果为不变那个数的平方减去变了那个数的平方,一定不要搞了。3、平方差公式的变式:根据不变那个数——a的位置,归纳出平方差公式的变式有四类八种:前头型、后头型、中间型、两头型。其中每一类都有正负两种。
前头型:(a+b)(a-b) =a2-b2 (-a+b)(-a-b) = (-a)2-b2
后头型:(b+a)(-b+a) = a2-b2 (b-a)(-b-a) =(-a)2-b2
中间型:(b+a)(a-b) = a2-b2 (b-a)(-a-b) =(-a)2-b2
两头型:(a+b)(-b+a) = a2-b2 (-a+b)(-b-a)=(-a)2-b2
4、平方差公式的作用:若两个二项式相乘满足平方差公式时,则可以直接写出结果。省去中间的各式相乘以及合并同类项,既快捷又准确。例题:(1)(2x-y)(2x+y)
(2)(3m-5n)(-5n-3m)
(3)(6-2b)(2b+6)
(4)(-3m-4n)(3m-4n)课堂练习:(1)(-m+n)(-m-n)
(2)(2a+5b)(-2a+5b)
(3)(5m-2)(-5m-2)
(4)(2x+3y)(3y-2x)
(5)(3a-5b)(5b+3a)
(6)(a+b+c)(a+b-c)课堂小结:1、是重要平方差公式的乘法公式之一。
2、它的作用在于:当两个二项式相乘符合平方差公式时,可以利用公式直接求出结果,既快捷又准确。
3、判断是否满足公式的条件是应用公式的前提。掌握公式的条件和四种变式是灵活运用平分差公式的基础。课外作业:P88页,习题A组、B组。
预习完全平方公式。
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
