邢台市第二十八中学冀教版七年级数学下册9.3三角形的角平分线、中线和高课件(共16张PPT)
文档属性
| 名称 | 邢台市第二十八中学冀教版七年级数学下册9.3三角形的角平分线、中线和高课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 275.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-08 00:00:00 | ||
图片预览




文档简介
课件16张PPT。 三角形的角平分线、中线和高教学目标 1.了解三角形的角平分线,中线和高的定义。
2.会画三角形的角平分线,中线和高。
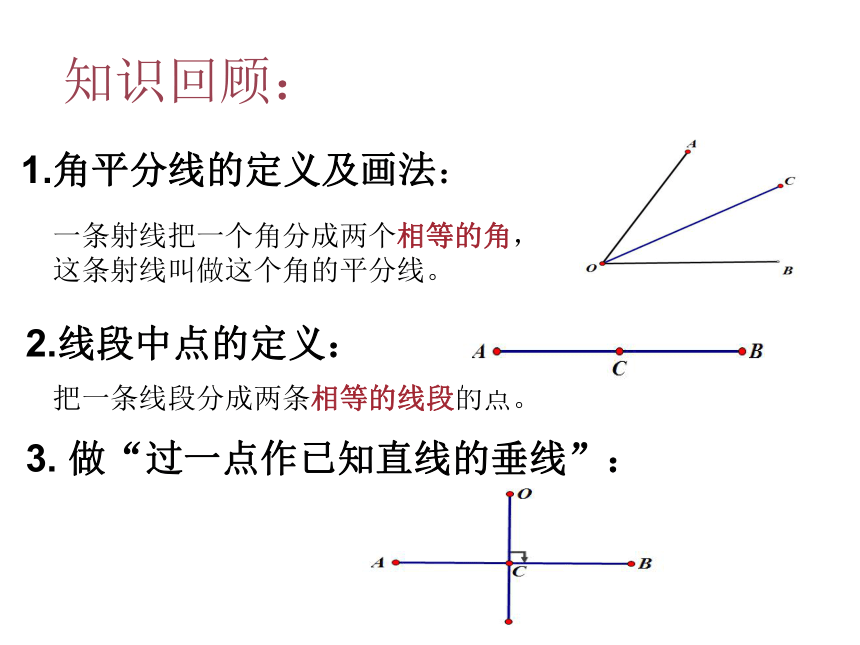
3.知道三角形的角平分线,中线和高的性质。2.线段中点的定义: 1.角平分线的定义及画法:3. 做“过一点作已知直线的垂线”:一条射线把一个角分成两个相等的角,
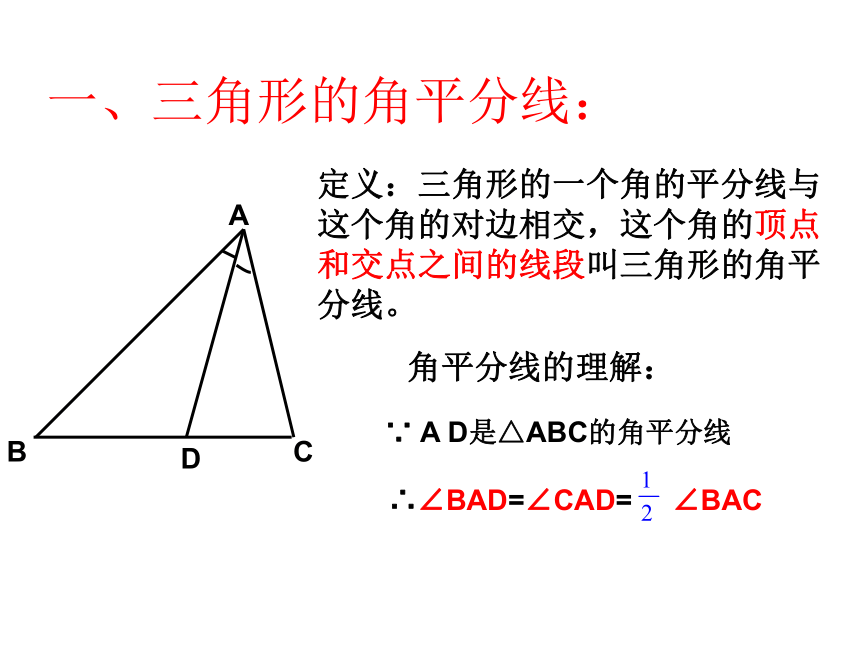
这条射线叫做这个角的平分线。把一条线段分成两条相等的线段的点。知识回顾:D一、三角形的角平分线:定义:三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫三角形的角平分线。角平分线的理解:∵ A D是△ABC的角平分线∴∠BAD=∠CAD= ∠BAC想一想,一个三角形有几条角平分线?请同学们画出,
思考它们有什么特点?①三角形的角平分线是一条线段,而角平分线是一条射线。
②一个三角形有三条角平分线,并且都在三角形的内部交于一点。
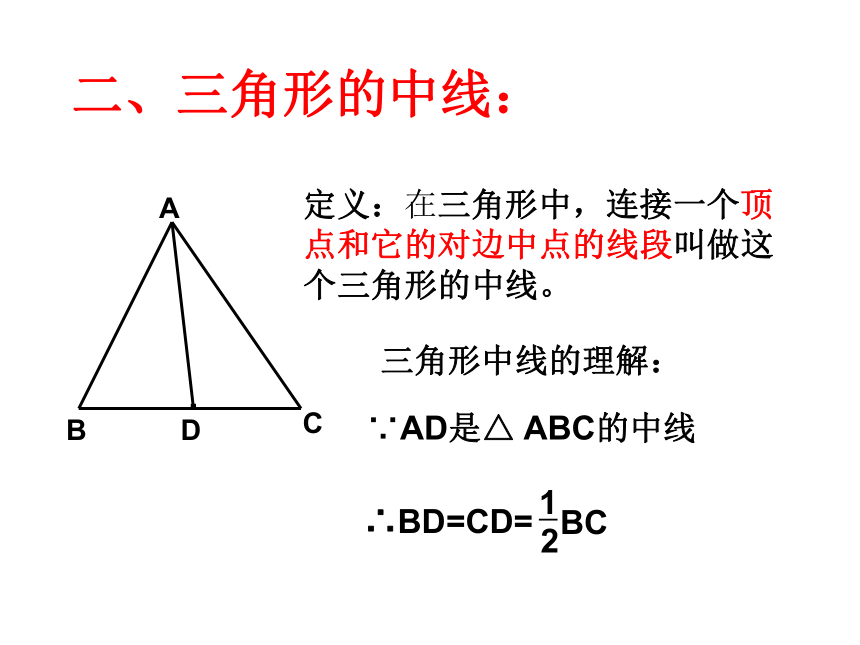
D.二、三角形的中线:定义:在三角形中,连接一个顶点和它的对边中点的线段叫做这个三角形的中线。
三角形中线的理解:∵AD是△ ABC的中线 想一想,一个三角形有几条中线?请同学们画出。
它们有什么特点?①三角形的中线是一条线段。
②任何三角形有三条中线,并且都在三角形的内部交于一点。
定义:从三角形一个顶点向它的对边所在的直线做垂线,顶点和垂足间的线段叫做三角形的高线,简称三角形的高。
D三、三角形的高: 对三角形高的理解:∵AD是△ ABC的高∴AD⊥BC或∠ADC=∠ADB=90° 想一想,一个三角形有几条高?请同学们用同样的方法画出。它们有什么特点?①三角形的高是一条线段。
②一个三角形有三条高,三条高(或高的延长线)相交于一点。可分为锐角三角形(内部),直角三角形(直角顶点),钝角三角形(外部)。巩固练习BD3、填空:
(1)如图(1),AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= , AE= 。
(2)如图(2), AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= , ∠ACB=2 。 AFCDAC∠2∠ABC∠4应用提高1、如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:
(1)BE= = ? ;
(2)∠BAD= = ? ;
(3)∠AFB= =90°;
CEBC∠CAD∠BAC∠AFC2、练习
如图,AE是 △ ABC的角平分线.已知∠B=500,
∠ C=600 ,求下列角的大小.CABE∠ CAE=_____∠ AEB=_____350950E3、右图所示,AD是△ABC的中线,则△ABD的面积和△ADC的面积数量关系?∵ AD是△ABC的中线∴BD=DC△ABD的面积= BD×AE
△ADC的面积= DC×AE故△ABD的面积= △ADC的面积知识总结 1.了解三角形的角平分线,中线和高的定义。
2.会画三角形的角平分线,中线和高。
3.知道三角形的角平分线,中线和高的性质。 作业:
2.会画三角形的角平分线,中线和高。
3.知道三角形的角平分线,中线和高的性质。2.线段中点的定义: 1.角平分线的定义及画法:3. 做“过一点作已知直线的垂线”:一条射线把一个角分成两个相等的角,
这条射线叫做这个角的平分线。把一条线段分成两条相等的线段的点。知识回顾:D一、三角形的角平分线:定义:三角形的一个角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫三角形的角平分线。角平分线的理解:∵ A D是△ABC的角平分线∴∠BAD=∠CAD= ∠BAC想一想,一个三角形有几条角平分线?请同学们画出,
思考它们有什么特点?①三角形的角平分线是一条线段,而角平分线是一条射线。
②一个三角形有三条角平分线,并且都在三角形的内部交于一点。
D.二、三角形的中线:定义:在三角形中,连接一个顶点和它的对边中点的线段叫做这个三角形的中线。
三角形中线的理解:∵AD是△ ABC的中线 想一想,一个三角形有几条中线?请同学们画出。
它们有什么特点?①三角形的中线是一条线段。
②任何三角形有三条中线,并且都在三角形的内部交于一点。
定义:从三角形一个顶点向它的对边所在的直线做垂线,顶点和垂足间的线段叫做三角形的高线,简称三角形的高。
D三、三角形的高: 对三角形高的理解:∵AD是△ ABC的高∴AD⊥BC或∠ADC=∠ADB=90° 想一想,一个三角形有几条高?请同学们用同样的方法画出。它们有什么特点?①三角形的高是一条线段。
②一个三角形有三条高,三条高(或高的延长线)相交于一点。可分为锐角三角形(内部),直角三角形(直角顶点),钝角三角形(外部)。巩固练习BD3、填空:
(1)如图(1),AD,BE,CF是ΔABC的三条中线,则AB=2 ,BD= , AE= 。
(2)如图(2), AD,BE,CF是ΔABC的三条角平分线,则∠1= , ∠3= , ∠ACB=2 。 AFCDAC∠2∠ABC∠4应用提高1、如图,在ΔABC中,AE是中线,AD是角平分线,AF是高。填空:
(1)BE= = ? ;
(2)∠BAD= = ? ;
(3)∠AFB= =90°;
CEBC∠CAD∠BAC∠AFC2、练习
如图,AE是 △ ABC的角平分线.已知∠B=500,
∠ C=600 ,求下列角的大小.CABE∠ CAE=_____∠ AEB=_____350950E3、右图所示,AD是△ABC的中线,则△ABD的面积和△ADC的面积数量关系?∵ AD是△ABC的中线∴BD=DC△ABD的面积= BD×AE
△ADC的面积= DC×AE故△ABD的面积= △ADC的面积知识总结 1.了解三角形的角平分线,中线和高的定义。
2.会画三角形的角平分线,中线和高。
3.知道三角形的角平分线,中线和高的性质。 作业:
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
