第十二章全等三角形添加辅助线专项练(含答案)2024--2025学年上学期初中数学人教版八年级上册
文档属性
| 名称 | 第十二章全等三角形添加辅助线专项练(含答案)2024--2025学年上学期初中数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 782.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-01 17:12:39 | ||
图片预览



文档简介
第十二章 全等三角形 添加辅助线 专项练
1.阅读理解:
(1)如图1,在中,若,,求边上的中线的取值范围.解决此问题可以用如下方法:延长到点,使得,再连接,把,,集中在中,利用三角形三边关系即可判断中线的取值范围是______.
(2)解决问题:如图2,在中,是边上的中点,,交于点,交于点,连接,求证:.
(3)问题拓展:如图3,在中,是边上的中点,延长至,使得,求证:.
2.已知:如图,在中,,D、E分别为上的点,且交于点F.若为的角平分线.
(1)求的度数;
(2)若,求的长.
3.如图,ABC中,AC=BC,∠ACB=90°,AD平分∠BAC交BC于点D,过点B作BE⊥AD,交AD延长线于点E,F为AB的中点,连接CF,交AD于点G,连接BG.
(1)线段BE与线段AD有何数量关系?并说明理由;
(2)判断BEG的形状,并说明理由.
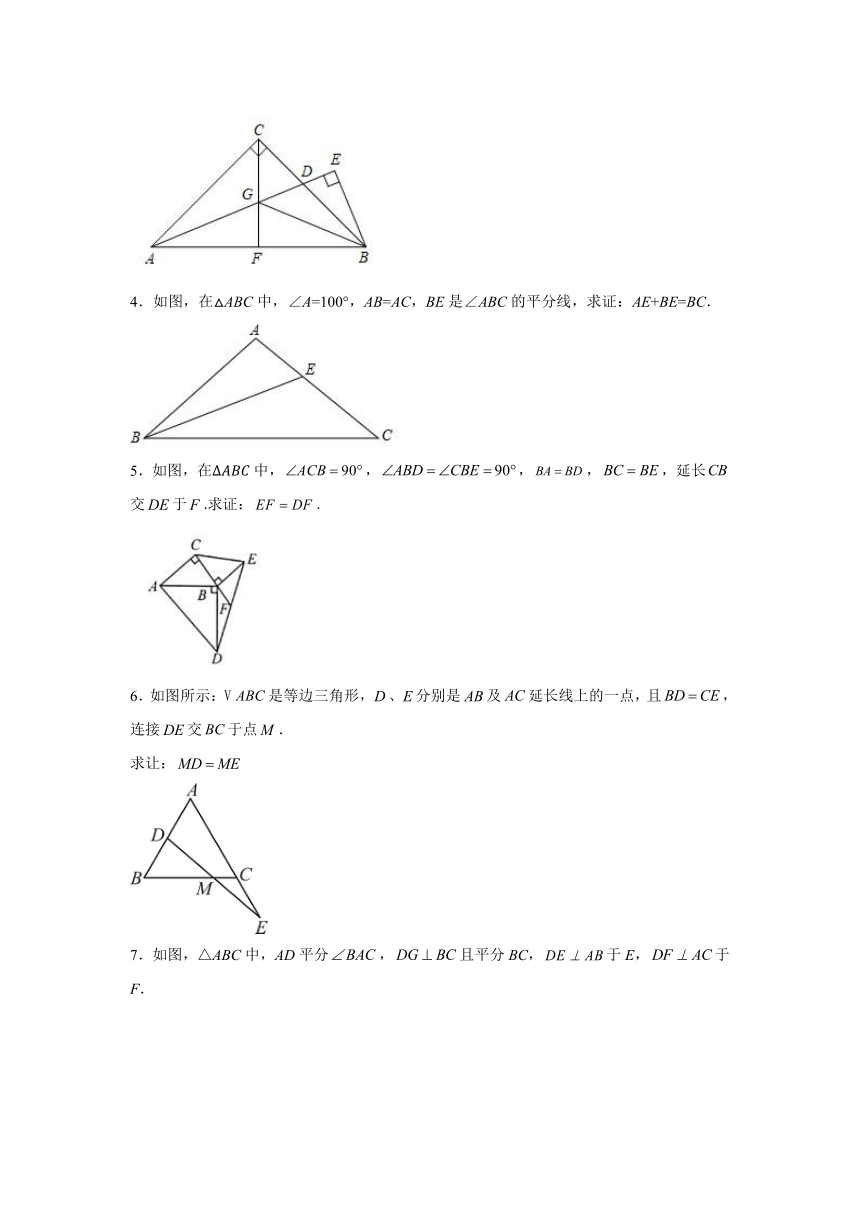
4.如图,在△ABC中,∠A=100°,AB=AC,BE是∠ABC的平分线,求证:AE+BE=BC.
5.如图,在中,,,,,延长交于.求证:.
6.如图所示:是等边三角形,、分别是及延长线上的一点,且,连接交于点.
求让:
7.如图,△ABC中,AD平分,且平分BC,于E,于F.
(1)证明:;
(2)如果,,求AE、BE的长.
8.已知:如图,AB=AE,BC=ED,AF是CD的垂直平分线,求证:∠B=∠E.
9.倍长中线法与作平行线是构造全等三角形常见的辅助线.
(1)如图1,在中,,中线,求的取值范围.方法一:延长到E使,连接;方法二:过点C作的平行线交的延长线于E.请你从以上两种方法中选一种方法证明,并直接写出的取值范围;
(2)如图2,在中,点B、D在上,,点D是的中点,若平分,求证:.
10.已知四边形中,,,,,绕B点旋转,它的两边分别交,(或它们的延长线)于E,F.
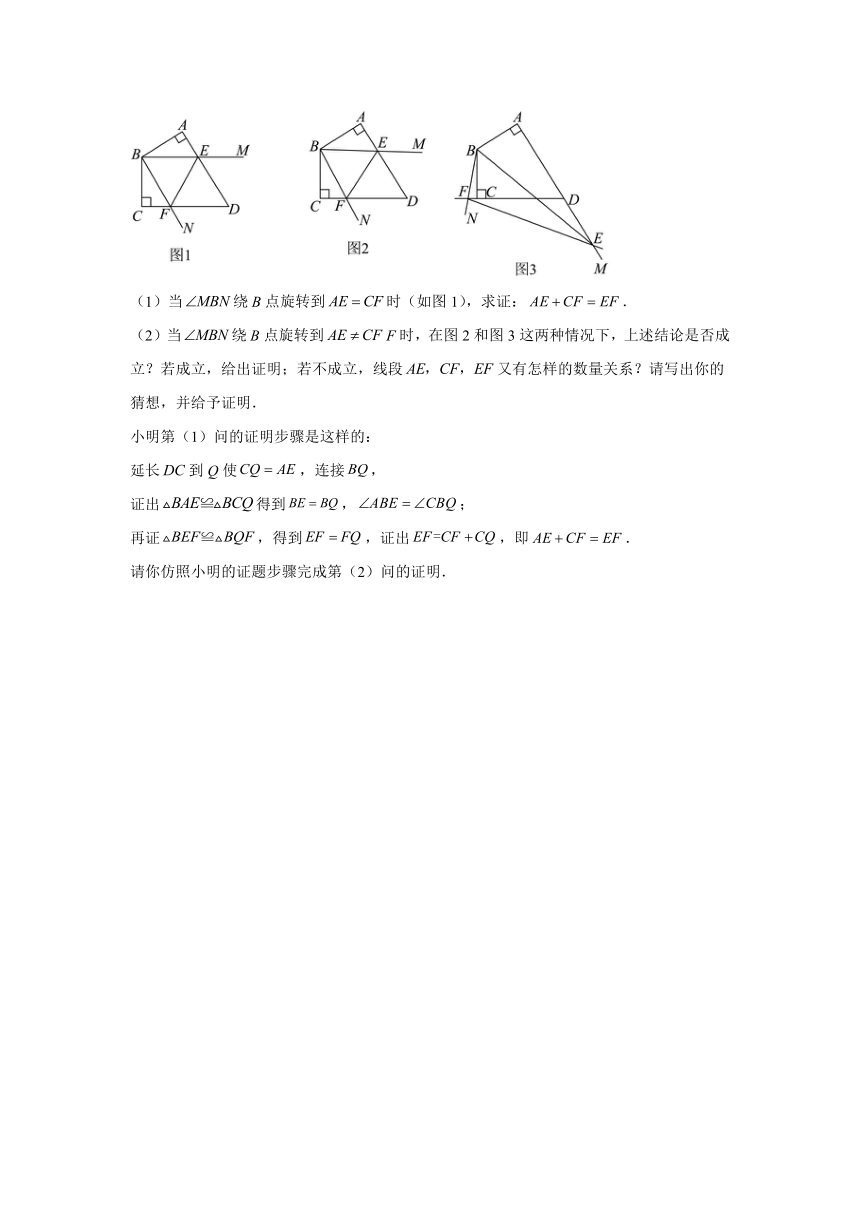
(1)当绕B点旋转到时(如图1),求证:.
(2)当绕B点旋转到F时,在图2和图3这两种情况下,上述结论是否成立?若成立,给出证明;若不成立,线段又有怎样的数量关系?请写出你的猜想,并给予证明.
小明第(1)问的证明步骤是这样的:
延长到Q使,连接,
证出得到,;
再证,得到,证出,即.
请你仿照小明的证题步骤完成第(2)问的证明.
参考答案:
1.(1);(2)见解析;(3)见解析.
(1)如图1延长到点,使得,再连接,
∵AD为中线,
∴BD=CD,
在△ADC和△ EDB中,
∵CD=BD,
∠ADC=∠EDB,
AD=ED,
∴△ACD≌△EBD(SAS),
∴AC=EB=6,
,
∵,
∴,
∴,
(2)如图2延长FD到G,使DG=FD,连结BG,EG,
由D为BC中点,BD=CD,
在△FDC和△GDB中,
∵CD=BD,
∠FDC=∠GDB,
FD=GD,
∴△FCD≌△GBD(SAS),
∴FC=GB,
∵,DF=DG,
∴EF=EG,
在△BEG中EG(3)如图3,延长AD到G使DG=AD,连结BG,
由是边上的中点,
∴BD=CD,
在△ADC和△GDB中,
∵CD=BD,
∠ADC=∠GDB,
AD=GD,
∴△ACD≌△GBD(SAS),
∴AC=GB,∠DAC=∠G,
∵BE=AC,
∴BE=BG,
∴∠BED=∠G=∠CAD.
2.(1)度
(2)
(1)解:∵为的角平分线,
∴
∵,
∴,
∴
(2)解:在上截取,连接.
∵为的角平分线.
∴,
∵,
∴,
∵
∴,
∴
∴,
又∵,
∴
∴,
∴
3.(1)BE=AD,见解析;(2)BEG是等腰直角三角形,见解析
证:(1)BE=AD,理由如下:
如图,延长BE、AC交于点H,
∵BE⊥AD,
∴∠AEB=∠AEH=90°,
∵AD平分∠BAC,
∴∠BAE=∠HAE,
在△BAE和△HAE中,
,
∴△BAE≌△HAE(ASA),
∴BE=HE=BH,
∵∠ACB=90°,
∴∠BCH=180°﹣∠ACB=90°=∠ACD,
∴∠CBH=90°﹣∠H=∠CAD,
在△BCH和△ACD中,
,
∴△BCH≌△ACD(ASA),
∴BH=AD,
∴BE=AD.
(2)△BEG是等腰直角三角形,理由如下:
∵AC=BC,AF=BF,
∴CF⊥AB,
∴AG=BG,
∴∠GAB=∠GBA,
∵AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∴∠GAB=∠CAB=22.5°,
∴∠GAB=∠GBA=22.5°,
∴∠EGB=∠GAB+∠GBA=45°,
∵∠BEG=90°,
∴∠EBG=∠EGB=45°,
∴EG=EB,
∴△BEG是等腰直角三角形.
4.见解析
解:如图,延长BE到F,使BF=BC,连接FC,
∵AB=AC,∠A=100°,
∴∠ABC=∠ACB=40°,
∵BE平分∠ABC,
∴∠ABE=∠EBC=20°,
∵BF=BC,
∴∠F=∠BCF=80°,
∴∠FCE=∠ACB=40°,
在BC上取CF′=CF,连接EF′,
在△FCE与△F′CE中,,
∴△FCE≌△F′CE(SAS),
∴EF=EF′,∠EF′C=∠F=80°,
∴∠BF′E=100°,
∴∠A=∠BF′E,
在△ABE与△F′BE中,,
∴△ABE≌△F′BE(AAS),
∴AE=EF′,
∴AE=EF,
∴AE+BE=BE+EF=BC.
5.详见解析
如图,过点D作的延长线于点G,
,
,
,
又∵∠ACB=∠BGD=90°,BA=BD,
∴,
,
又∵BC=BE,
,
又∵∠EBF=∠DGF=90°,∠EFB=∠DFG,
∴,
∴EF=DF.
【点睛】
6.见详解
过点D作DF∥AC,交BC于点F,
∵是等边三角形,
∴∠B=∠ACB=60°,
∵DF∥AC,
∴∠DFB=∠ACB=60°,∠MDF=∠MEC,
∴是等边三角形,
∴BD=DF,
∵,
∴DF=CE,
又∵∠FMD=∠CME,
∴ FMD CME,
∴.
7.(1)见解析
(2)AE=4,BE=1
(1)证明:如图,连接BD、CD,
∵且平分BC,
∴BD=CD,
∵AD平分,于E,于F,
∴DE=CF,∠DEB=∠DFC=90°,
在Rt△BED与Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:∵AD平分,于E,于F,
∴DE=DF,∠DEB=∠DFC=90°,
在Rt△AED与Rt△AFD中,
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∴CF=AF-AC=AE-AC,
由(1)知:BE=CF,
∴AB-AE=AE-AC
即5-AE=AE-3,
∴AE=4,
∴BE=AB-AE=5-4=1,
8.略
【详解】证明:连接AC,AD
∵AF⊥CD且F是CD的中点
∴可知AF是CD的垂直平分线,
线段垂直平分线上的点到线段两端的距离相等
∴AC=AD,
在和中
9.(1)
(2)证明见解析
(1)解:选方法一来证明,
是的中线,
在和中
,
,
在中,
,
,
即:,
,
(2)解:延长到F使,连接,如图所示;
点D是的中点,
,
在和中,
,
,
,
平分,
,
,
在和中,
,
,
.
10.(1)见解析(2)图2成立;图3不成立,见解析
(1)如图,延长到Q使,连接,
∵,,,
,
∴,,
∵,
∴,
∴,,
∴即,
∵,
∴,
∵,
∴,
∴,
∵,,
∴.
∴.
(2)图2成立,图3不成立.
证明:如图2,延长到K使,连接,
∵,,,
,
∴,,
∵,
∴,
∴,,
∴即,
∵,
∴,
∵,
∴,
∴,
∵,,
∴.
∴.
如图3,如图,延长到Q使,连接,
∵,,,
,
∴,
∵,
∴,
∴,,
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴.
∴.
1.阅读理解:
(1)如图1,在中,若,,求边上的中线的取值范围.解决此问题可以用如下方法:延长到点,使得,再连接,把,,集中在中,利用三角形三边关系即可判断中线的取值范围是______.
(2)解决问题:如图2,在中,是边上的中点,,交于点,交于点,连接,求证:.
(3)问题拓展:如图3,在中,是边上的中点,延长至,使得,求证:.
2.已知:如图,在中,,D、E分别为上的点,且交于点F.若为的角平分线.
(1)求的度数;
(2)若,求的长.
3.如图,ABC中,AC=BC,∠ACB=90°,AD平分∠BAC交BC于点D,过点B作BE⊥AD,交AD延长线于点E,F为AB的中点,连接CF,交AD于点G,连接BG.
(1)线段BE与线段AD有何数量关系?并说明理由;
(2)判断BEG的形状,并说明理由.
4.如图,在△ABC中,∠A=100°,AB=AC,BE是∠ABC的平分线,求证:AE+BE=BC.
5.如图,在中,,,,,延长交于.求证:.
6.如图所示:是等边三角形,、分别是及延长线上的一点,且,连接交于点.
求让:
7.如图,△ABC中,AD平分,且平分BC,于E,于F.
(1)证明:;
(2)如果,,求AE、BE的长.
8.已知:如图,AB=AE,BC=ED,AF是CD的垂直平分线,求证:∠B=∠E.
9.倍长中线法与作平行线是构造全等三角形常见的辅助线.
(1)如图1,在中,,中线,求的取值范围.方法一:延长到E使,连接;方法二:过点C作的平行线交的延长线于E.请你从以上两种方法中选一种方法证明,并直接写出的取值范围;
(2)如图2,在中,点B、D在上,,点D是的中点,若平分,求证:.
10.已知四边形中,,,,,绕B点旋转,它的两边分别交,(或它们的延长线)于E,F.
(1)当绕B点旋转到时(如图1),求证:.
(2)当绕B点旋转到F时,在图2和图3这两种情况下,上述结论是否成立?若成立,给出证明;若不成立,线段又有怎样的数量关系?请写出你的猜想,并给予证明.
小明第(1)问的证明步骤是这样的:
延长到Q使,连接,
证出得到,;
再证,得到,证出,即.
请你仿照小明的证题步骤完成第(2)问的证明.
参考答案:
1.(1);(2)见解析;(3)见解析.
(1)如图1延长到点,使得,再连接,
∵AD为中线,
∴BD=CD,
在△ADC和△ EDB中,
∵CD=BD,
∠ADC=∠EDB,
AD=ED,
∴△ACD≌△EBD(SAS),
∴AC=EB=6,
,
∵,
∴,
∴,
(2)如图2延长FD到G,使DG=FD,连结BG,EG,
由D为BC中点,BD=CD,
在△FDC和△GDB中,
∵CD=BD,
∠FDC=∠GDB,
FD=GD,
∴△FCD≌△GBD(SAS),
∴FC=GB,
∵,DF=DG,
∴EF=EG,
在△BEG中EG
由是边上的中点,
∴BD=CD,
在△ADC和△GDB中,
∵CD=BD,
∠ADC=∠GDB,
AD=GD,
∴△ACD≌△GBD(SAS),
∴AC=GB,∠DAC=∠G,
∵BE=AC,
∴BE=BG,
∴∠BED=∠G=∠CAD.
2.(1)度
(2)
(1)解:∵为的角平分线,
∴
∵,
∴,
∴
(2)解:在上截取,连接.
∵为的角平分线.
∴,
∵,
∴,
∵
∴,
∴
∴,
又∵,
∴
∴,
∴
3.(1)BE=AD,见解析;(2)BEG是等腰直角三角形,见解析
证:(1)BE=AD,理由如下:
如图,延长BE、AC交于点H,
∵BE⊥AD,
∴∠AEB=∠AEH=90°,
∵AD平分∠BAC,
∴∠BAE=∠HAE,
在△BAE和△HAE中,
,
∴△BAE≌△HAE(ASA),
∴BE=HE=BH,
∵∠ACB=90°,
∴∠BCH=180°﹣∠ACB=90°=∠ACD,
∴∠CBH=90°﹣∠H=∠CAD,
在△BCH和△ACD中,
,
∴△BCH≌△ACD(ASA),
∴BH=AD,
∴BE=AD.
(2)△BEG是等腰直角三角形,理由如下:
∵AC=BC,AF=BF,
∴CF⊥AB,
∴AG=BG,
∴∠GAB=∠GBA,
∵AC=BC,∠ACB=90°,
∴∠CAB=∠CBA=45°,
∴∠GAB=∠CAB=22.5°,
∴∠GAB=∠GBA=22.5°,
∴∠EGB=∠GAB+∠GBA=45°,
∵∠BEG=90°,
∴∠EBG=∠EGB=45°,
∴EG=EB,
∴△BEG是等腰直角三角形.
4.见解析
解:如图,延长BE到F,使BF=BC,连接FC,
∵AB=AC,∠A=100°,
∴∠ABC=∠ACB=40°,
∵BE平分∠ABC,
∴∠ABE=∠EBC=20°,
∵BF=BC,
∴∠F=∠BCF=80°,
∴∠FCE=∠ACB=40°,
在BC上取CF′=CF,连接EF′,
在△FCE与△F′CE中,,
∴△FCE≌△F′CE(SAS),
∴EF=EF′,∠EF′C=∠F=80°,
∴∠BF′E=100°,
∴∠A=∠BF′E,
在△ABE与△F′BE中,,
∴△ABE≌△F′BE(AAS),
∴AE=EF′,
∴AE=EF,
∴AE+BE=BE+EF=BC.
5.详见解析
如图,过点D作的延长线于点G,
,
,
,
又∵∠ACB=∠BGD=90°,BA=BD,
∴,
,
又∵BC=BE,
,
又∵∠EBF=∠DGF=90°,∠EFB=∠DFG,
∴,
∴EF=DF.
【点睛】
6.见详解
过点D作DF∥AC,交BC于点F,
∵是等边三角形,
∴∠B=∠ACB=60°,
∵DF∥AC,
∴∠DFB=∠ACB=60°,∠MDF=∠MEC,
∴是等边三角形,
∴BD=DF,
∵,
∴DF=CE,
又∵∠FMD=∠CME,
∴ FMD CME,
∴.
7.(1)见解析
(2)AE=4,BE=1
(1)证明:如图,连接BD、CD,
∵且平分BC,
∴BD=CD,
∵AD平分,于E,于F,
∴DE=CF,∠DEB=∠DFC=90°,
在Rt△BED与Rt△CFD中,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:∵AD平分,于E,于F,
∴DE=DF,∠DEB=∠DFC=90°,
在Rt△AED与Rt△AFD中,
,
∴Rt△AED≌Rt△AFD(HL),
∴AE=AF,
∴CF=AF-AC=AE-AC,
由(1)知:BE=CF,
∴AB-AE=AE-AC
即5-AE=AE-3,
∴AE=4,
∴BE=AB-AE=5-4=1,
8.略
【详解】证明:连接AC,AD
∵AF⊥CD且F是CD的中点
∴可知AF是CD的垂直平分线,
线段垂直平分线上的点到线段两端的距离相等
∴AC=AD,
在和中
9.(1)
(2)证明见解析
(1)解:选方法一来证明,
是的中线,
在和中
,
,
在中,
,
,
即:,
,
(2)解:延长到F使,连接,如图所示;
点D是的中点,
,
在和中,
,
,
,
平分,
,
,
在和中,
,
,
.
10.(1)见解析(2)图2成立;图3不成立,见解析
(1)如图,延长到Q使,连接,
∵,,,
,
∴,,
∵,
∴,
∴,,
∴即,
∵,
∴,
∵,
∴,
∴,
∵,,
∴.
∴.
(2)图2成立,图3不成立.
证明:如图2,延长到K使,连接,
∵,,,
,
∴,,
∵,
∴,
∴,,
∴即,
∵,
∴,
∵,
∴,
∴,
∵,,
∴.
∴.
如图3,如图,延长到Q使,连接,
∵,,,
,
∴,
∵,
∴,
∴,,
∴,
∵,
∴,
∵,
∴,
∴,
∵,,
∴.
∴.
