第十一章至第十二章 三角形和全等三角形综合试题(含详解)2024--2025学年上学期初中数学人教版八年级上册
文档属性
| 名称 | 第十一章至第十二章 三角形和全等三角形综合试题(含详解)2024--2025学年上学期初中数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-01 00:00:00 | ||
图片预览


文档简介
第十一章至第十二章 三角形和全等三角形 综合试题
一、单选题
1.下列说法中,正确的个数有( )
(1)三角形具有稳定性;
(2)三角形的角平分线是射线;
(3)任何一个三角形都有三条高、三条中线、三条角平分线;
(4)三角形的三条角平分线交于一点,且这点在三角形内;
A.1 B.2 C.3 D.4
2.脊柱侧弯是指脊柱的一个或数个节段向侧方弯曲或伴有椎体旋转的脊柱畸形,医学上常用角来评估脊柱侧弯的程度,当角为脊柱侧弯.如图是脊柱侧弯角的检测示意图,于于,已知角为,则的大小是( )
A. B. C. D.
3.如图,把三角形纸片折叠,使得点,点都与点重合,折痕分别为,,若,则的度数为( )
A. B. C. D.
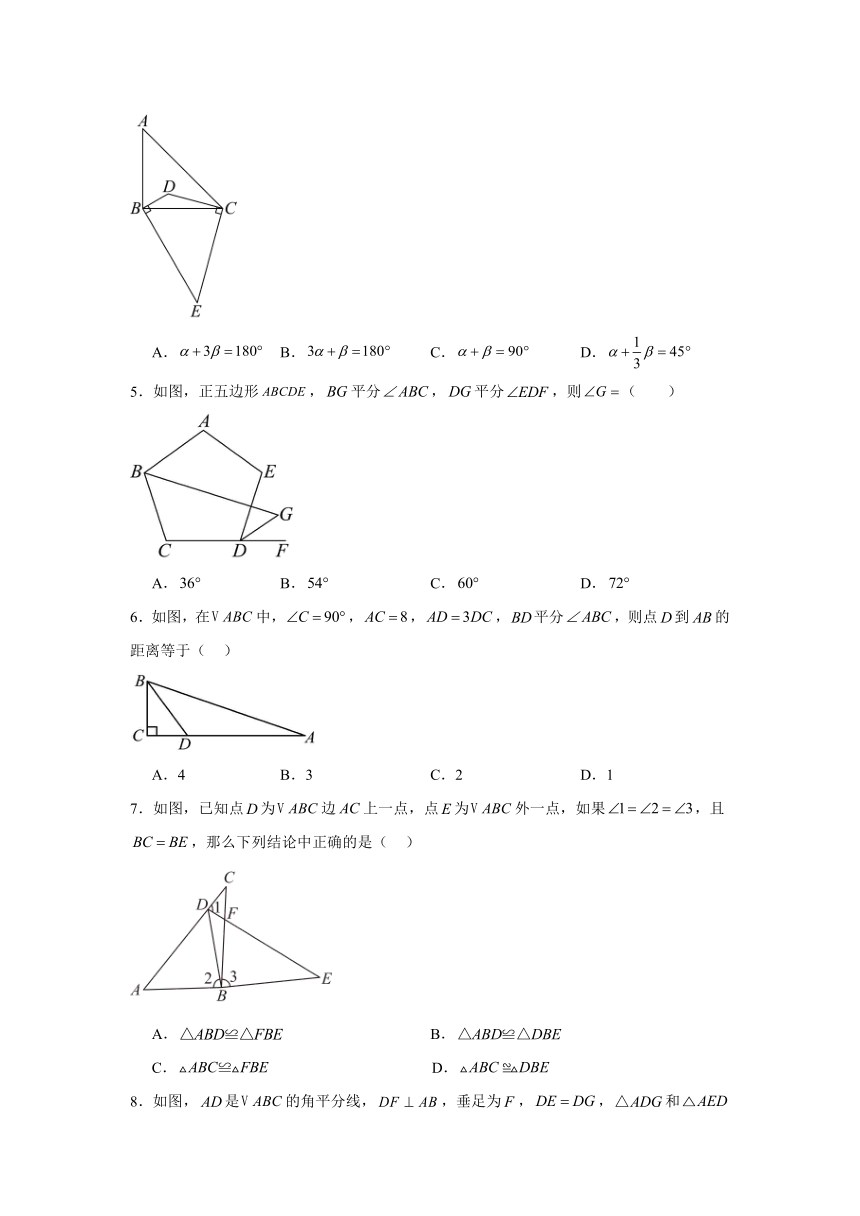
4.如图,点D为内一点,满足,,过点B,点C分别作的垂线相交于点E.设,,则与之间的数量关系为( )
A. B. C. D.
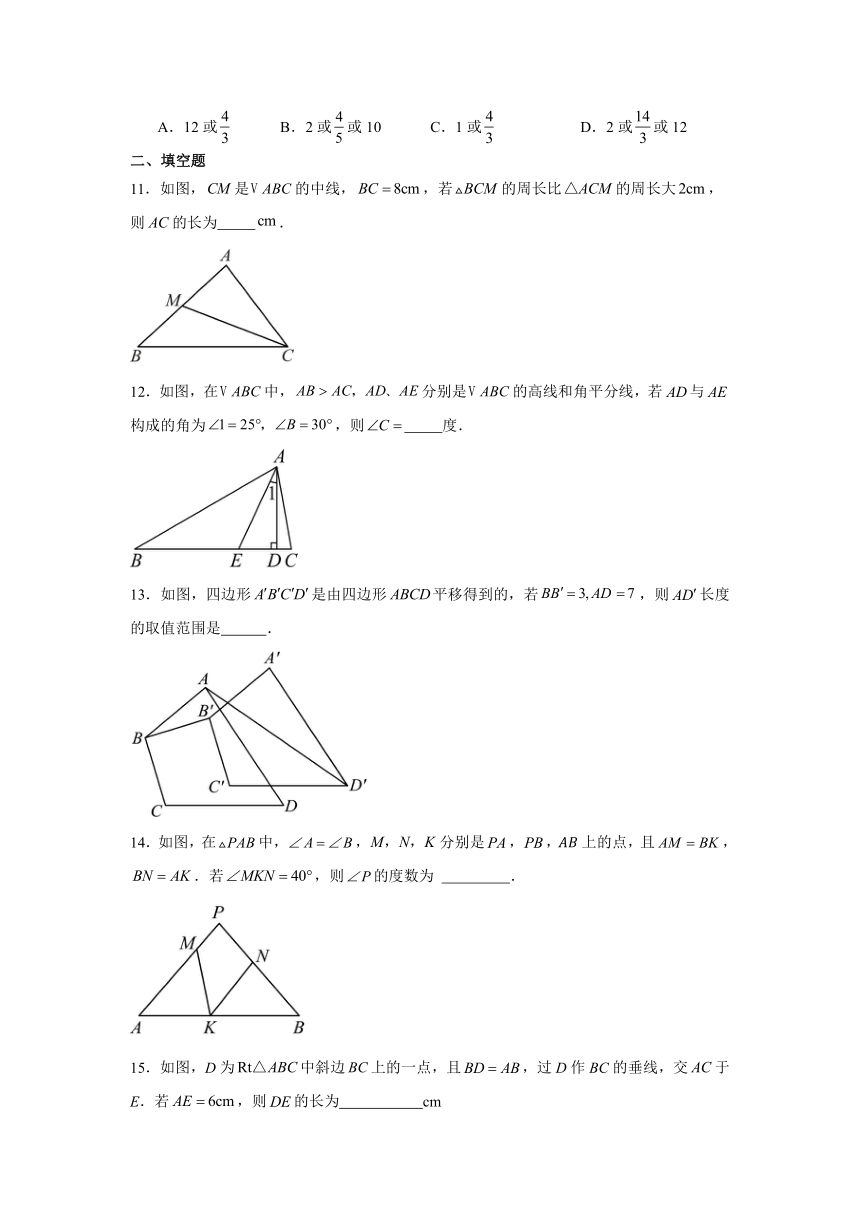
5.如图,正五边形,平分,平分,则( )
A. B. C. D.
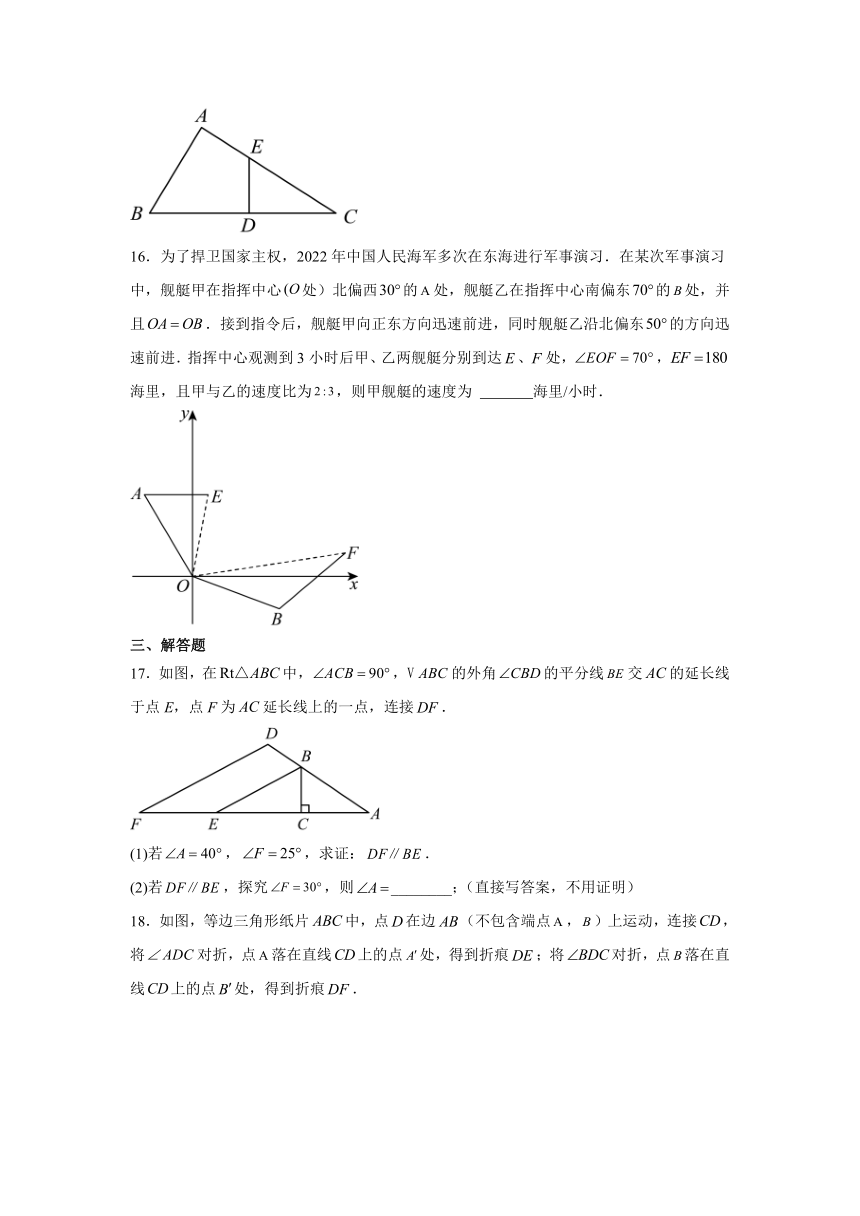
6.如图,在中,,,,平分,则点到的距离等于( )
A.4 B.3 C.2 D.1
7.如图,已知点为边上一点,点为外一点,如果,且,那么下列结论中正确的是( )
A. B.
C. D.
8.如图,是的角平分线,,垂足为,,和的面积分别为48和26,则的面积为( )
A.11 B.22 C.26 D.37
9.已知,,,其中.点P以每秒2个单位长度的速度,沿着路径运动.同时,点Q以每秒x个单位长度的速度,沿着路径运动,一个点到达终点后另一个点随即停止运动.它们的运动时间为 t 秒.
①若,则点P运动路程始终是点Q运动路程的2倍;
②当P、Q两点同时到达A点时,;
③若,,时,与垂直;
④若与全等,则或.
以上说法正确的选项为( )
A.①② B.①②③ C.①②④ D.①②③④
10.如图,中,,,,直线经过点且与边相交.动点从点出发沿路径向终点运动;动点从点出发沿路径向终点运动.点和点的速度分别为和,两点同时出发并开始计时,当点到达终点时计时结束.在某时刻分别过点和点作于点,于点,设运动时间为秒,则当为( )秒时,与全等.
A.12或 B.2或或10 C.1或 D.2或或12
二、填空题
11.如图,是的中线,,若的周长比的周长大,则的长为 .
12.如图,在中,分别是的高线和角平分线,若与构成的角为,则 度.
13.如图,四边形是由四边形平移得到的,若,则长度的取值范围是 .
14.如图,在中,,分别是,,上的点,且,.若,则的度数为 .
15.如图,D为中斜边上的一点,且,过D作BC的垂线,交于E.若,则的长为 cm
16.为了捍卫国家主权,2022年中国人民海军多次在东海进行军事演习.在某次军事演习中,舰艇甲在指挥中心处)北偏西的处,舰艇乙在指挥中心南偏东的处,并且.接到指令后,舰艇甲向正东方向迅速前进,同时舰艇乙沿北偏东的方向迅速前进.指挥中心观测到3小时后甲、乙两舰艇分别到达、处,,海里,且甲与乙的速度比为,则甲舰艇的速度为 海里/小时.
三、解答题
17.如图,在中,,的外角的平分线交的延长线于点E,点F为延长线上的一点,连接.
(1)若,,求证:.
(2)若,探究,则________;(直接写答案,不用证明)
18.如图,等边三角形纸片中,点在边(不包含端点,)上运动,连接,将对折,点落在直线上的点处,得到折痕;将对折,点落在直线上的点处,得到折痕.
(1)若,求的度数;
(2)试问:的大小是否会随着点的运动而变化?若不变,求出的度数;若变化,请说明理由.
19.如图,已知:A、F、C、D在同一条直线上,,,.求证:
(1);
(2).
20.如图,在中,,点D是边上一点,,且,与交于点G,过点E作交于点F,交于点H.
(1)求证:;
(2)若,求的值.
21.如图,点、、、在同一条直线上,,,
(1)求证:;
(2)若,,求的度数.
参考答案:
1.C
解:(1)三角形具有稳定性;描述正确,
(2)三角形的角平分线是线段;原来描述错误;
(3)任何一个三角形都有三条高、三条中线、三条角平分线;描述正确;
(4)三角形的三条角平分线交于一点,且这点在三角形内;描述正确;
2.A
解:,,
,
,
,,
,
3.A
解:∵,,
∴,
由折叠的性质可得:,,
∴,
∵,
∴,
4.A
解:,
,
,,
,
,
,
即
,
,
即,
解得,
5.B
如图:
∵正五边形中,,平分,
∴,
∵,平分正五边形的外角,
∴,
∴,
∴.
6.C
解:过点作于点,如图所示,
,,
.
,
,
,平分,
.
点到的距离等于2.
7.D
解:∵,
∴,即,
∵
∴,
又,
∴
∴选项D正确;
而选项A、B、C都无法证明三角形全等,
8.A
解:如图,作于,
是的角平分线,,,
,
在和中,
,
,
同理,,
设的面积为,由题意得,
,
解得,
即的面积为11,
9.C
解:①∵点P以每秒2个单位长度的速度,运动时间为 t 秒,
∴点P运动路程为,
若,则点Q运动路程为,
∴点P运动路程始终是点Q运动路程的2倍,故①正确;
②当P点到达A点时,秒,
∵P、Q两点同时到达A点,
∴,故②正确;
③如图所示,
当,时,
点P运动的路程为,点Q运动的路程为,
∵,
∴,,
∵
∴
∴
∴和不全等
∴
∵
∴
∴
∴与不垂直,故③错误;
④当时,
∴,即,
,即
解得,,
当时,
∴,即,
,即
解得,.
∴若与全等,则或,故④正确.
综上所述,正确的选项为①②④.
10.D
解:①如图1,Q在上,点P在上时,作,
由题意得,,
∵,
∴,
∵,
∴,
∴,
当时,
则,
即,
解得:;
②如图2,当点P与点Q重合时,
由题意得,,
∵,
∴,
当,
则,
∴,
解得:;
③如图3,当点Q与A重合时,
由题意得,,
∵,
∴,
∵,
∴,
当,
则,
即,
解得:;
当综上所述:当秒或秒或12秒时,与全等,
11.
∵是的中线,
∴,
由的周长为,的周长,
∵的周长比的周长大,
∴,
∵,
∴,
故答案为:.
12.
解:∵,
∴,
在中, , ,
∴,
∴,
∵平分,
∴
在中,,
∴
故答案为:.
13.
解:连接,如图所示,
∵四边形是由四边形平移得到的,
∴,
∵,
∴,
∴,
即,
故答案为:.
14./100度
解:在和中,
,
∴,
∴,
∵是的外角,
∴,
∴,
∴,
∴,
故答案为:.
15.6
连接.
在和中,
,
∴,
∴.
故答案为:6.
16.24
如图,连接,延长、相交于点,延长到,使,
由题意得,,
,
,
,
,
,
∴,
,,
,
,
,
,
,
∴,
(海里),
设甲的速度为海里小时,乙的速度为海里小时,
海里,海里,
,
,
,
答:甲的速度为24海里小时,
故答案为:24.
17.(1)见详解
(2)
(1)证明:∵,,
,
∵平分,
,
,
又,
,
;
(2)解:∵,
,
∵是的平分线,
,
,
,
∴,
∵.
∴.
18.(1)
(2)不变,
(1)解:∵将对折,得到折痕,
∴,
∵将对折,得到折痕,
∴,
∵,
∴,
∴.
(2)解:不变.理由如下:
∵,,,
∴,
即.
∴的大小不随点的运动而变化.
19.(1)见解析
(2)见解析
(1)证明:如图:在和中,
,
∴,
∴,
∴;
(2)证明:由(1)得,
在和中,
,
∴,
∴.
20.(1)见解析
(2)
(1)证明:,
,
,
,
,
.
(2)解:,,
,
,,
.
21.(1)见解析
(2)
(1)证明:∵
∴,即
∵,
∴
(2)∵,,
∴,
∵,
∴
一、单选题
1.下列说法中,正确的个数有( )
(1)三角形具有稳定性;
(2)三角形的角平分线是射线;
(3)任何一个三角形都有三条高、三条中线、三条角平分线;
(4)三角形的三条角平分线交于一点,且这点在三角形内;
A.1 B.2 C.3 D.4
2.脊柱侧弯是指脊柱的一个或数个节段向侧方弯曲或伴有椎体旋转的脊柱畸形,医学上常用角来评估脊柱侧弯的程度,当角为脊柱侧弯.如图是脊柱侧弯角的检测示意图,于于,已知角为,则的大小是( )
A. B. C. D.
3.如图,把三角形纸片折叠,使得点,点都与点重合,折痕分别为,,若,则的度数为( )
A. B. C. D.
4.如图,点D为内一点,满足,,过点B,点C分别作的垂线相交于点E.设,,则与之间的数量关系为( )
A. B. C. D.
5.如图,正五边形,平分,平分,则( )
A. B. C. D.
6.如图,在中,,,,平分,则点到的距离等于( )
A.4 B.3 C.2 D.1
7.如图,已知点为边上一点,点为外一点,如果,且,那么下列结论中正确的是( )
A. B.
C. D.
8.如图,是的角平分线,,垂足为,,和的面积分别为48和26,则的面积为( )
A.11 B.22 C.26 D.37
9.已知,,,其中.点P以每秒2个单位长度的速度,沿着路径运动.同时,点Q以每秒x个单位长度的速度,沿着路径运动,一个点到达终点后另一个点随即停止运动.它们的运动时间为 t 秒.
①若,则点P运动路程始终是点Q运动路程的2倍;
②当P、Q两点同时到达A点时,;
③若,,时,与垂直;
④若与全等,则或.
以上说法正确的选项为( )
A.①② B.①②③ C.①②④ D.①②③④
10.如图,中,,,,直线经过点且与边相交.动点从点出发沿路径向终点运动;动点从点出发沿路径向终点运动.点和点的速度分别为和,两点同时出发并开始计时,当点到达终点时计时结束.在某时刻分别过点和点作于点,于点,设运动时间为秒,则当为( )秒时,与全等.
A.12或 B.2或或10 C.1或 D.2或或12
二、填空题
11.如图,是的中线,,若的周长比的周长大,则的长为 .
12.如图,在中,分别是的高线和角平分线,若与构成的角为,则 度.
13.如图,四边形是由四边形平移得到的,若,则长度的取值范围是 .
14.如图,在中,,分别是,,上的点,且,.若,则的度数为 .
15.如图,D为中斜边上的一点,且,过D作BC的垂线,交于E.若,则的长为 cm
16.为了捍卫国家主权,2022年中国人民海军多次在东海进行军事演习.在某次军事演习中,舰艇甲在指挥中心处)北偏西的处,舰艇乙在指挥中心南偏东的处,并且.接到指令后,舰艇甲向正东方向迅速前进,同时舰艇乙沿北偏东的方向迅速前进.指挥中心观测到3小时后甲、乙两舰艇分别到达、处,,海里,且甲与乙的速度比为,则甲舰艇的速度为 海里/小时.
三、解答题
17.如图,在中,,的外角的平分线交的延长线于点E,点F为延长线上的一点,连接.
(1)若,,求证:.
(2)若,探究,则________;(直接写答案,不用证明)
18.如图,等边三角形纸片中,点在边(不包含端点,)上运动,连接,将对折,点落在直线上的点处,得到折痕;将对折,点落在直线上的点处,得到折痕.
(1)若,求的度数;
(2)试问:的大小是否会随着点的运动而变化?若不变,求出的度数;若变化,请说明理由.
19.如图,已知:A、F、C、D在同一条直线上,,,.求证:
(1);
(2).
20.如图,在中,,点D是边上一点,,且,与交于点G,过点E作交于点F,交于点H.
(1)求证:;
(2)若,求的值.
21.如图,点、、、在同一条直线上,,,
(1)求证:;
(2)若,,求的度数.
参考答案:
1.C
解:(1)三角形具有稳定性;描述正确,
(2)三角形的角平分线是线段;原来描述错误;
(3)任何一个三角形都有三条高、三条中线、三条角平分线;描述正确;
(4)三角形的三条角平分线交于一点,且这点在三角形内;描述正确;
2.A
解:,,
,
,
,,
,
3.A
解:∵,,
∴,
由折叠的性质可得:,,
∴,
∵,
∴,
4.A
解:,
,
,,
,
,
,
即
,
,
即,
解得,
5.B
如图:
∵正五边形中,,平分,
∴,
∵,平分正五边形的外角,
∴,
∴,
∴.
6.C
解:过点作于点,如图所示,
,,
.
,
,
,平分,
.
点到的距离等于2.
7.D
解:∵,
∴,即,
∵
∴,
又,
∴
∴选项D正确;
而选项A、B、C都无法证明三角形全等,
8.A
解:如图,作于,
是的角平分线,,,
,
在和中,
,
,
同理,,
设的面积为,由题意得,
,
解得,
即的面积为11,
9.C
解:①∵点P以每秒2个单位长度的速度,运动时间为 t 秒,
∴点P运动路程为,
若,则点Q运动路程为,
∴点P运动路程始终是点Q运动路程的2倍,故①正确;
②当P点到达A点时,秒,
∵P、Q两点同时到达A点,
∴,故②正确;
③如图所示,
当,时,
点P运动的路程为,点Q运动的路程为,
∵,
∴,,
∵
∴
∴
∴和不全等
∴
∵
∴
∴
∴与不垂直,故③错误;
④当时,
∴,即,
,即
解得,,
当时,
∴,即,
,即
解得,.
∴若与全等,则或,故④正确.
综上所述,正确的选项为①②④.
10.D
解:①如图1,Q在上,点P在上时,作,
由题意得,,
∵,
∴,
∵,
∴,
∴,
当时,
则,
即,
解得:;
②如图2,当点P与点Q重合时,
由题意得,,
∵,
∴,
当,
则,
∴,
解得:;
③如图3,当点Q与A重合时,
由题意得,,
∵,
∴,
∵,
∴,
当,
则,
即,
解得:;
当综上所述:当秒或秒或12秒时,与全等,
11.
∵是的中线,
∴,
由的周长为,的周长,
∵的周长比的周长大,
∴,
∵,
∴,
故答案为:.
12.
解:∵,
∴,
在中, , ,
∴,
∴,
∵平分,
∴
在中,,
∴
故答案为:.
13.
解:连接,如图所示,
∵四边形是由四边形平移得到的,
∴,
∵,
∴,
∴,
即,
故答案为:.
14./100度
解:在和中,
,
∴,
∴,
∵是的外角,
∴,
∴,
∴,
∴,
故答案为:.
15.6
连接.
在和中,
,
∴,
∴.
故答案为:6.
16.24
如图,连接,延长、相交于点,延长到,使,
由题意得,,
,
,
,
,
,
∴,
,,
,
,
,
,
,
∴,
(海里),
设甲的速度为海里小时,乙的速度为海里小时,
海里,海里,
,
,
,
答:甲的速度为24海里小时,
故答案为:24.
17.(1)见详解
(2)
(1)证明:∵,,
,
∵平分,
,
,
又,
,
;
(2)解:∵,
,
∵是的平分线,
,
,
,
∴,
∵.
∴.
18.(1)
(2)不变,
(1)解:∵将对折,得到折痕,
∴,
∵将对折,得到折痕,
∴,
∵,
∴,
∴.
(2)解:不变.理由如下:
∵,,,
∴,
即.
∴的大小不随点的运动而变化.
19.(1)见解析
(2)见解析
(1)证明:如图:在和中,
,
∴,
∴,
∴;
(2)证明:由(1)得,
在和中,
,
∴,
∴.
20.(1)见解析
(2)
(1)证明:,
,
,
,
,
.
(2)解:,,
,
,,
.
21.(1)见解析
(2)
(1)证明:∵
∴,即
∵,
∴
(2)∵,,
∴,
∵,
∴
