第一节 地图和地图投影课件
图片预览









文档简介
课件68张PPT。第一节 地图和地图投影第一节 地图和地图投影(1)识记并领会地图投影的概念,地图投影变形概念、变形椭圆及各种变形的表示
(2)识记并领会方位投影的构成原理以及平射方位投影、等积方位投影、等距方位投影
的投影条件、投影后经纬线形状、变形规律,了解它们的用途。
(3)识记并领会圆柱投影的构成原理,正轴等角圆柱投影的投影条件、投影后经纬线形状、变形规律及其用途。第一节 地图和地图投影(4)识记并领会高斯—克吕格投影的投影构成、投影后经纬网形状、变形规律、高斯投影带划分、高斯平面直角坐标系和用途。
(5)识记并领会圆锥投影的构成原理以及等角圆锥投影、等积圆锥投影、等距圆锥投影的投影条件、变形规律,了解它们的用途。
(6)了解普通多圆锥投影的概念,等差分纬线多圆锥投影、彭纳投影和桑生投影的特点。
(7)了解选择地图投影的主要考虑因素。第一节 地图投影的基本问题一、地图投影的概念
二、地图投影的意义
三、地图投影的变形
四、地图投影的分类
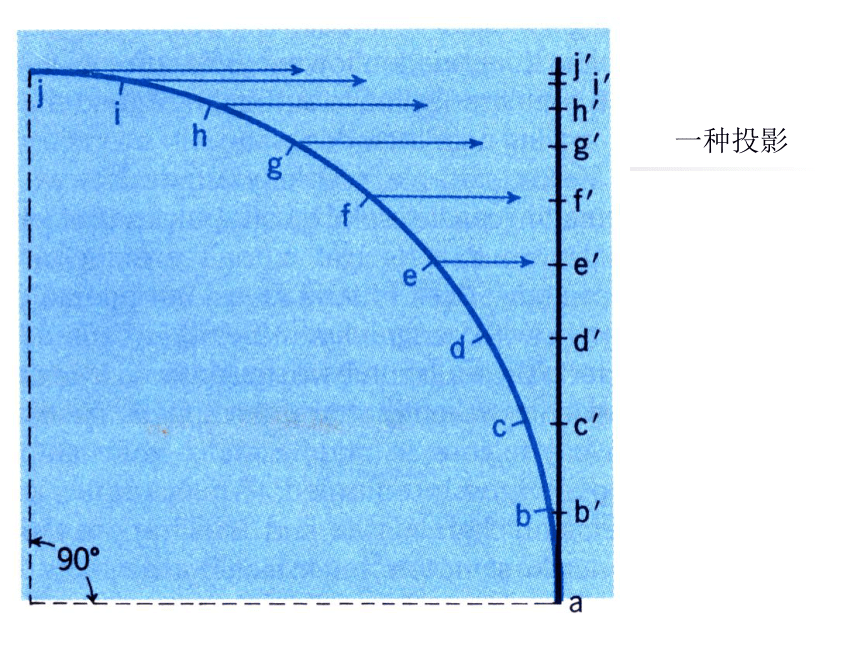
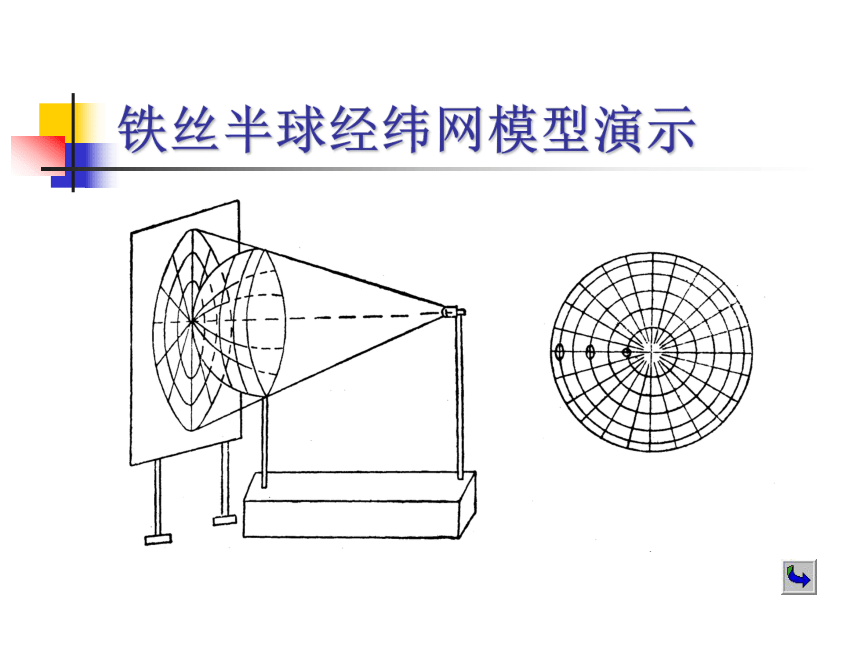
一、地图投影的概念在地球球面和平面之间建立点与点之间函数关系的数学方法。一种投影铁丝半球经纬网模型演示二、地图投影的意义
(1)若不使用地图投影,可用地球仪直接模拟地球,但不细致,不精确,使用不方便,不能满足所有社会需求。应用上需要把客观世界表现在有限的平面上。二、地图投影的意义
(2) 地球表面为不可展曲面,随意展成平面,必然产生无规律变形,因此必须建立科学的投影关系,控制变形和误差。二、地图投影的意义
(3)地图投影尽管不能避免误差,但可求其误差规律,可根据需要,选择适宜的投影方式。三、地图投影的变形(一)地图投影变形
(二)变形椭圆
(一)地图投影变形设想光源的远近对经纬网的影响光源置于球心
纬线间距自极点至赤道由内向外不断拉伸
投影后赤道在无穷远处光源置于无穷远
纬线间距自极点至赤道由内向外不断压缩,赤道附近趋零
纬线被赤道圈围光源置于球心外有限距离,光线弯曲——(等距数学函数法)
纬线间距不变
投影后赤道半径为子午面上极点至赤道的距离光源置于球心外有限距离,光线弯曲——(等积数学函数法)
面积不变,纬线间距自极点至赤道由内向外逐步压缩
投影后两纬圈之间的纬度带的面积保持不变地图投影变形几种不同投影的经纬线形式球面经纬网投影前后差异
投影前球面经纬网的特征:
纬线长度不等
同一条纬线,经差相同的纬线弧长相等
经线长度相等
梯形网格(经度带、纬度带)
经线和纬线呈直角相交球面经纬网投影前后差异投影后变形的表现:
长度变形:地图上的长度随不同地点和方向而改变
面积变形:地图上的面积随不同地点而改变
角度变形:地图上两条线所夹的角度不等于球面上相应的角度(二)变形椭圆1.定义
2.用变形椭圆说明各种变形
1 .定义
球面上的微小圆,投影后变为椭圆(特殊情况下为圆),这种椭圆叫变形椭圆。xyX’Y’mnm’n’O O’?证明椭圆过程a=x’/x a=x’/m
b=y’/y b=y’/n
因为 x2+y2=1
所以 x’2/a2+ y’2/b2=1
此方程即为以0’为原点,以投影后相交成?角的经纬线为两共轭直径的斜坐标椭圆方程。2.用变形椭圆说明各种变形 (1) 长度比和长度变形
(2) 面积比和面积变形
(3) 角度变形(1)长度比和长度变形长度比
主方向
主比例尺和局部比例尺
长度变形
比例尺和长度变形的关系长度比长度比
μ=投影后长度/原长度
=椭圆半径/小圆半径=ds’/ds
地图投影后长度比随不同地点和方向而变
长度比地图投影研究四个特殊方向的长度比:
经线方向长度比m,
纬线方向长度比n,
最大方向长度比a,
最小方向长度比b。mmnab共轭椭圆的性质决定:
a2+b2 = m2+n2 a*b = m*n*sin?长度变形(Vu)指长度比与1的差值,即Vu =μ-1。
Vu = 0 无长度变形
Vu > 0 正长度变形
Vu < 0 负长度变形主方向在变形椭圆中,椭圆的长轴方向和短轴方向,分别表示最大长度比和最小长度比,两方向互相垂直,称为主方向。主比例尺和局部比例尺运用地图投影方法绘制经纬网时,首先把地球椭球体按规定的比例尺缩小,然后把它表示在平面上,这个比例尺就是主比例尺。
主比例尺和局部比例尺地图除了符合主比例尺的地方以外,其它地方大于或小于主比例尺,这种比例尺叫局部比例尺。(2)面积比和面积变形 面积比
P= 椭圆面积/小圆面积
= πabl2/π12 = ab
(2)面积比和面积变形 面积变形VP 为面积比与1之差(P-1)
P=1 VP=0 无面积变形
P>1 VP>0 正面积变形
P<1 VP<0 负面积变形
(3)角度变形在许许多多的角度变形值中,一定有一个最大值,通常在提到角度变形时,主要研究最大角度变形。角度变形证明理解2点:
同一象限中,变形最大的角度应该是相对主方向的角度角度变形证明最大角度变形为一个象限中最大角度变形的2倍。角度变形证明角度变形证明四、地图投影的分类(一)按变形性质分类
(二)按构成方法分类
(一)按变形性质分类1.等角投影(正形投影)
2.等积投影
3.任意投影
4. 各种变形性质投影的关系1.等角投影(正形投影)定义:投影图上没有角度变形,即ω=0的投影。1.等角投影(正形投影)数学式:a=b
变形椭圆:为圆,它表明在等角投影中,任一点上的长度比不随方向的改变而改变。1.等角投影(正形投影)
用途:局部图形与实地相似。航海图、洋流图、风向图等。2.等积投影定义:没有面积变形,即面积比等于1的投影。
2.等积投影数学式:P=ab=1 或 a=1/b b=1/a
变形椭圆:为椭圆,面积相等,但形状变化较大。2.等积投影
用途:自然、经济地图,对面积精度要求高。3.任意投影既不等积又不等角的投影。3.任意投影
一种特殊的任意投影:
等距投影:主方向之一没有长度变形的投影。3.任意投影
等距投影数学式:a=1 或 b=1
等距投影变形椭圆:为椭圆,面积变形小于等角投影,角度变形小于等积投影。3.任意投影等距投影用途:一般参考用途和教学用途。4. 各种变形性质投影的关系——在等积投影上不能保持等角特性,在等角投影上不能保持等积特性。4. 各种变形性质投影的关系
——在任意投影上不能保持等角和等积的特性4. 各种变形性质投影的关系——等积投影的形状变形比较大,等角投影的面积变形比较大(二)按构成方法分类1.几何投影
2.非几何投影1.几何投影(借助几何面)几何面形式不同
方位投影(几何面为平面)
圆柱投影(几何面为圆柱)
圆锥投影(几何面为圆锥) 1.几何投影(借助几何面)
球面与投影面相对部位不同
正轴
横轴
斜轴 方位投影 正轴 横轴 斜轴正轴投影经纬网圆柱投影 正轴 横轴 斜轴正轴投影经纬网圆锥投影 正轴 横轴 斜轴
正轴投影经纬网正轴投影经纬线形状
方位 圆柱 圆锥2.非几何投影(数学解析法)不借助几何面,用数学解析法确定
伪方位投影
伪圆柱投影
伪圆锥投影
多圆锥投影伪方位投影伪方位投影 伪圆柱投影 伪圆锥投影伪圆锥投影 多圆锥投影多圆锥投影
(2)识记并领会方位投影的构成原理以及平射方位投影、等积方位投影、等距方位投影
的投影条件、投影后经纬线形状、变形规律,了解它们的用途。
(3)识记并领会圆柱投影的构成原理,正轴等角圆柱投影的投影条件、投影后经纬线形状、变形规律及其用途。第一节 地图和地图投影(4)识记并领会高斯—克吕格投影的投影构成、投影后经纬网形状、变形规律、高斯投影带划分、高斯平面直角坐标系和用途。
(5)识记并领会圆锥投影的构成原理以及等角圆锥投影、等积圆锥投影、等距圆锥投影的投影条件、变形规律,了解它们的用途。
(6)了解普通多圆锥投影的概念,等差分纬线多圆锥投影、彭纳投影和桑生投影的特点。
(7)了解选择地图投影的主要考虑因素。第一节 地图投影的基本问题一、地图投影的概念
二、地图投影的意义
三、地图投影的变形
四、地图投影的分类
一、地图投影的概念在地球球面和平面之间建立点与点之间函数关系的数学方法。一种投影铁丝半球经纬网模型演示二、地图投影的意义
(1)若不使用地图投影,可用地球仪直接模拟地球,但不细致,不精确,使用不方便,不能满足所有社会需求。应用上需要把客观世界表现在有限的平面上。二、地图投影的意义
(2) 地球表面为不可展曲面,随意展成平面,必然产生无规律变形,因此必须建立科学的投影关系,控制变形和误差。二、地图投影的意义
(3)地图投影尽管不能避免误差,但可求其误差规律,可根据需要,选择适宜的投影方式。三、地图投影的变形(一)地图投影变形
(二)变形椭圆
(一)地图投影变形设想光源的远近对经纬网的影响光源置于球心
纬线间距自极点至赤道由内向外不断拉伸
投影后赤道在无穷远处光源置于无穷远
纬线间距自极点至赤道由内向外不断压缩,赤道附近趋零
纬线被赤道圈围光源置于球心外有限距离,光线弯曲——(等距数学函数法)
纬线间距不变
投影后赤道半径为子午面上极点至赤道的距离光源置于球心外有限距离,光线弯曲——(等积数学函数法)
面积不变,纬线间距自极点至赤道由内向外逐步压缩
投影后两纬圈之间的纬度带的面积保持不变地图投影变形几种不同投影的经纬线形式球面经纬网投影前后差异
投影前球面经纬网的特征:
纬线长度不等
同一条纬线,经差相同的纬线弧长相等
经线长度相等
梯形网格(经度带、纬度带)
经线和纬线呈直角相交球面经纬网投影前后差异投影后变形的表现:
长度变形:地图上的长度随不同地点和方向而改变
面积变形:地图上的面积随不同地点而改变
角度变形:地图上两条线所夹的角度不等于球面上相应的角度(二)变形椭圆1.定义
2.用变形椭圆说明各种变形
1 .定义
球面上的微小圆,投影后变为椭圆(特殊情况下为圆),这种椭圆叫变形椭圆。xyX’Y’mnm’n’O O’?证明椭圆过程a=x’/x a=x’/m
b=y’/y b=y’/n
因为 x2+y2=1
所以 x’2/a2+ y’2/b2=1
此方程即为以0’为原点,以投影后相交成?角的经纬线为两共轭直径的斜坐标椭圆方程。2.用变形椭圆说明各种变形 (1) 长度比和长度变形
(2) 面积比和面积变形
(3) 角度变形(1)长度比和长度变形长度比
主方向
主比例尺和局部比例尺
长度变形
比例尺和长度变形的关系长度比长度比
μ=投影后长度/原长度
=椭圆半径/小圆半径=ds’/ds
地图投影后长度比随不同地点和方向而变
长度比地图投影研究四个特殊方向的长度比:
经线方向长度比m,
纬线方向长度比n,
最大方向长度比a,
最小方向长度比b。mmnab共轭椭圆的性质决定:
a2+b2 = m2+n2 a*b = m*n*sin?长度变形(Vu)指长度比与1的差值,即Vu =μ-1。
Vu = 0 无长度变形
Vu > 0 正长度变形
Vu < 0 负长度变形主方向在变形椭圆中,椭圆的长轴方向和短轴方向,分别表示最大长度比和最小长度比,两方向互相垂直,称为主方向。主比例尺和局部比例尺运用地图投影方法绘制经纬网时,首先把地球椭球体按规定的比例尺缩小,然后把它表示在平面上,这个比例尺就是主比例尺。
主比例尺和局部比例尺地图除了符合主比例尺的地方以外,其它地方大于或小于主比例尺,这种比例尺叫局部比例尺。(2)面积比和面积变形 面积比
P= 椭圆面积/小圆面积
= πabl2/π12 = ab
(2)面积比和面积变形 面积变形VP 为面积比与1之差(P-1)
P=1 VP=0 无面积变形
P>1 VP>0 正面积变形
P<1 VP<0 负面积变形
(3)角度变形在许许多多的角度变形值中,一定有一个最大值,通常在提到角度变形时,主要研究最大角度变形。角度变形证明理解2点:
同一象限中,变形最大的角度应该是相对主方向的角度角度变形证明最大角度变形为一个象限中最大角度变形的2倍。角度变形证明角度变形证明四、地图投影的分类(一)按变形性质分类
(二)按构成方法分类
(一)按变形性质分类1.等角投影(正形投影)
2.等积投影
3.任意投影
4. 各种变形性质投影的关系1.等角投影(正形投影)定义:投影图上没有角度变形,即ω=0的投影。1.等角投影(正形投影)数学式:a=b
变形椭圆:为圆,它表明在等角投影中,任一点上的长度比不随方向的改变而改变。1.等角投影(正形投影)
用途:局部图形与实地相似。航海图、洋流图、风向图等。2.等积投影定义:没有面积变形,即面积比等于1的投影。
2.等积投影数学式:P=ab=1 或 a=1/b b=1/a
变形椭圆:为椭圆,面积相等,但形状变化较大。2.等积投影
用途:自然、经济地图,对面积精度要求高。3.任意投影既不等积又不等角的投影。3.任意投影
一种特殊的任意投影:
等距投影:主方向之一没有长度变形的投影。3.任意投影
等距投影数学式:a=1 或 b=1
等距投影变形椭圆:为椭圆,面积变形小于等角投影,角度变形小于等积投影。3.任意投影等距投影用途:一般参考用途和教学用途。4. 各种变形性质投影的关系——在等积投影上不能保持等角特性,在等角投影上不能保持等积特性。4. 各种变形性质投影的关系
——在任意投影上不能保持等角和等积的特性4. 各种变形性质投影的关系——等积投影的形状变形比较大,等角投影的面积变形比较大(二)按构成方法分类1.几何投影
2.非几何投影1.几何投影(借助几何面)几何面形式不同
方位投影(几何面为平面)
圆柱投影(几何面为圆柱)
圆锥投影(几何面为圆锥) 1.几何投影(借助几何面)
球面与投影面相对部位不同
正轴
横轴
斜轴 方位投影 正轴 横轴 斜轴正轴投影经纬网圆柱投影 正轴 横轴 斜轴正轴投影经纬网圆锥投影 正轴 横轴 斜轴
正轴投影经纬网正轴投影经纬线形状
方位 圆柱 圆锥2.非几何投影(数学解析法)不借助几何面,用数学解析法确定
伪方位投影
伪圆柱投影
伪圆锥投影
多圆锥投影伪方位投影伪方位投影 伪圆柱投影 伪圆锥投影伪圆锥投影 多圆锥投影多圆锥投影
