物理人教版(2019)必修第一册3.5共点力的平衡 课件(共32张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第一册3.5共点力的平衡 课件(共32张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-01 21:59:53 | ||
图片预览




文档简介
(共32张PPT)
G
Ff
A
B
C
FN
Gx
Gy
θ
共点力的平衡
一、平衡状态
1.定义:物体在几个力作用下保持静止或匀速直线运动的状态,叫平衡状态。
3.v=0,就是静止吗?
不是,静止是一种平衡态,v=0,如竖直上抛最高点,此时仅受重力,不平衡。
缓慢移动,是移动速度无限小,运动中各点处于准“静止”状态,这种状态可视为平衡状态,蕴含着极限思想。
2.处于平衡状态的物体其加速度是多大?
静止、匀速、缓慢移动,加速度a=0
4.“静止”和“v=0”的区别和联系
v=0
合力为0,即a=0时,静止,处于平衡状态
合力不为0,即a≠0时,不静止,非平衡态,如,竖直上抛运动的最高点时刻
1、二力平衡的条件:
二、共点力的平衡条件
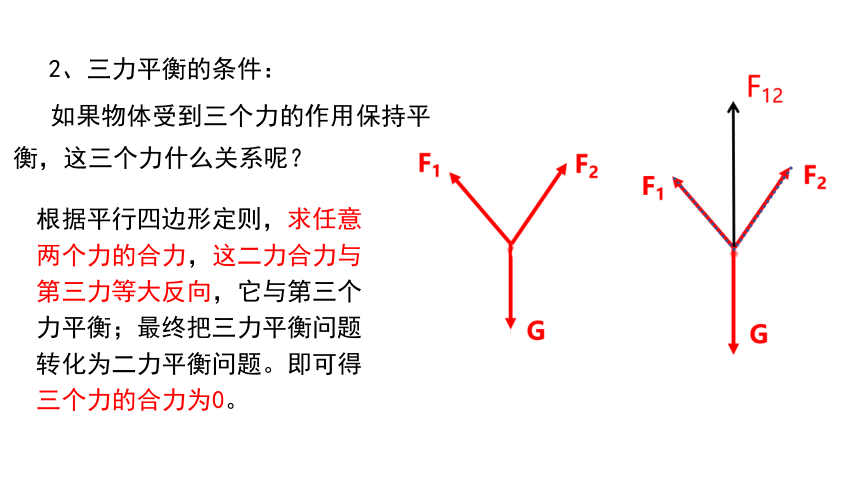
两个力等大、反向,共线。即:合力为零。
F拉
mg
·
如果物体受到三个力的作用保持平衡,这三个力什么关系呢?
根据平行四边形定则,求任意两个力的合力,这二力合力与第三力等大反向,它与第三个力平衡;最终把三力平衡问题转化为二力平衡问题。即可得三个力的合力为0。
2、三力平衡的条件:
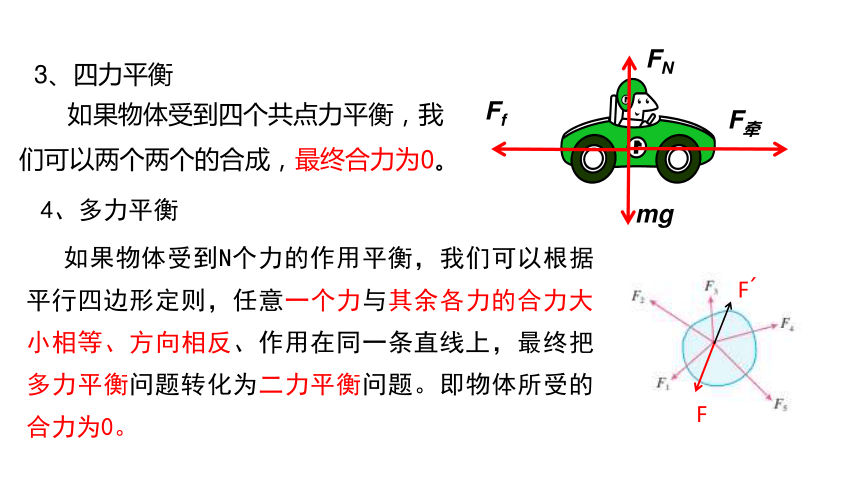
如果物体受到四个共点力平衡,我们可以两个两个的合成,最终合力为0。
mg
FN
F牵
Ff
3、四力平衡
如果物体受到N个力的作用平衡,我们可以根据平行四边形定则,任意一个力与其余各力的合力大小相等、方向相反、作用在同一条直线上,最终把多力平衡问题转化为二力平衡问题。即物体所受的合力为0。
4、多力平衡
F
F
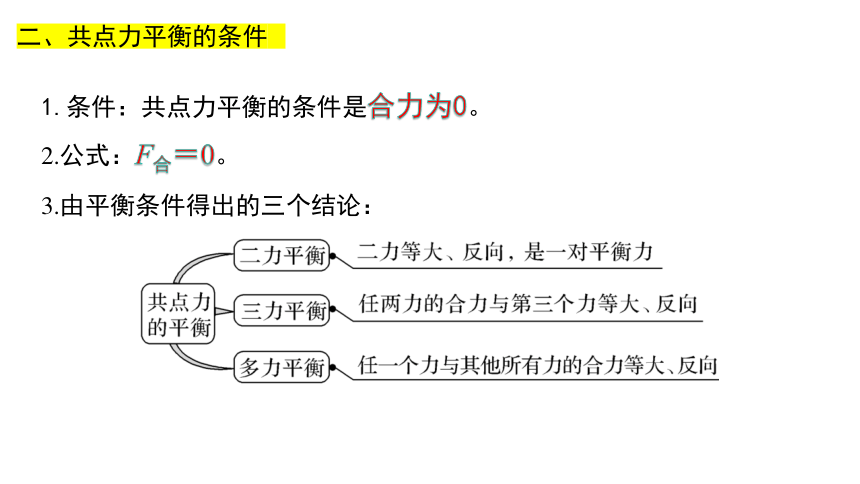
二、共点力平衡的条件
1.条件:共点力平衡的条件是合力为0。
2.公式:F合=0。
3.由平衡条件得出的三个结论:
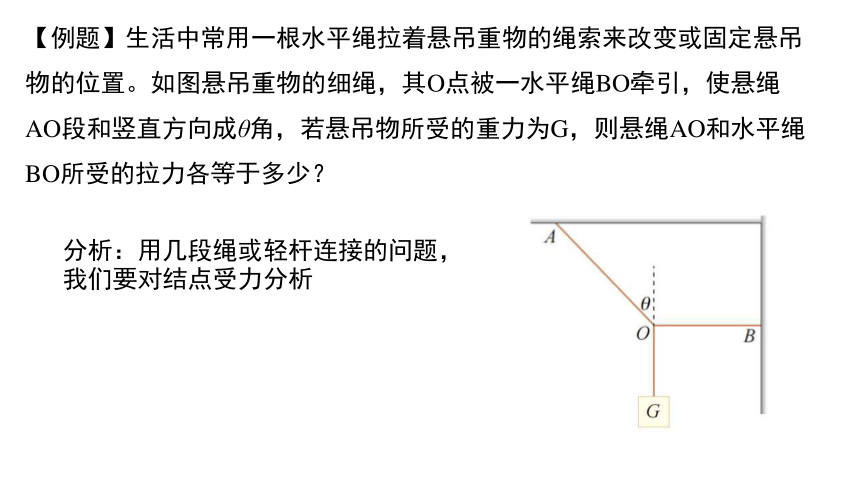
【例题】生活中常用一根水平绳拉着悬吊重物的绳索来改变或固定悬吊物的位置。如图悬吊重物的细绳,其O点被一水平绳BO牵引,使悬绳AO段和竖直方向成θ角,若悬吊物所受的重力为G,则悬绳AO和水平绳BO所受的拉力各等于多少?
分析:用几段绳或轻杆连接的问题,我们要对结点受力分析
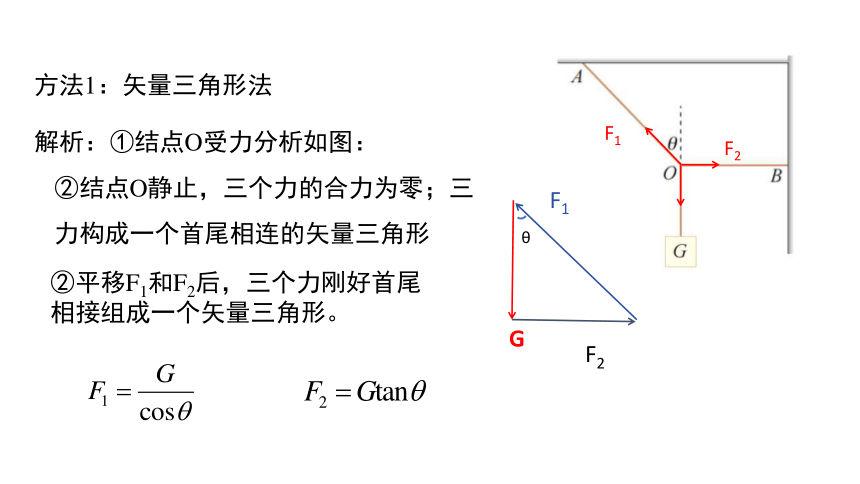
方法1:矢量三角形法
解析:①结点O受力分析如图:
F1
F2
②结点O静止,三个力的合力为零;三力构成一个首尾相连的矢量三角形
②平移F1和F2后,三个力刚好首尾相接组成一个矢量三角形。
F1
F2
G
θ
方法2:正交分解法
①如图,对结点O受力分析,
解得:F1=G/cosθ,F2=Gtanθ。
F1
F2
F1x
F1y
②将F1正交分解在水平、竖直两个方向,分别为F1x 和F1y 。因为结点合力为0,因此x、y两方向上的合力都等于0,则:
F2 =F1x
F1y = G
F2 = F1sinθ
F1cosθ=G
【例题2】某幼儿园要在空地上做一个滑梯,根据空地的大小,滑梯的水平跨度确定为6m。设计时,滑板和儿童裤料之间的动摩擦因数取0.4,为使儿童在滑 梯游戏时能在滑板上滑下,滑梯至少要多高?
A
B
C
解:
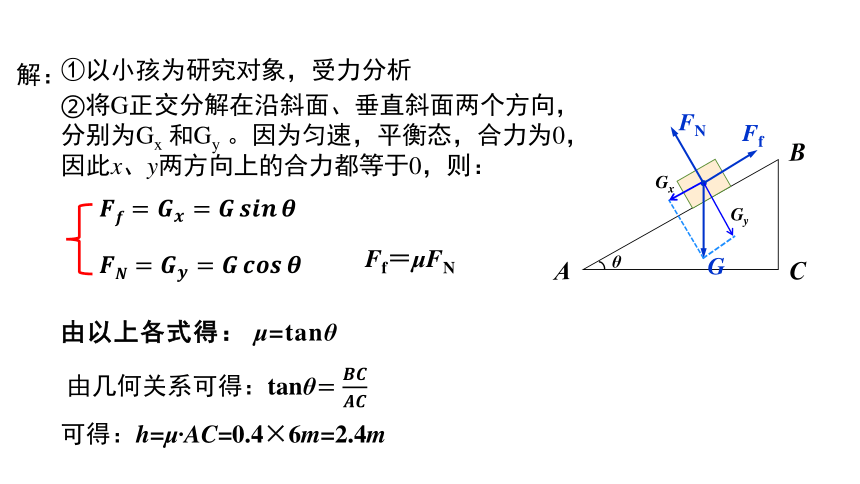
①以小孩为研究对象,受力分析
Ff=μFN
由以上各式得: μ=tanθ
由几何关系可得:tanθ
可得:h=μ·AC=0.4×6m=2.4m
G
Ff
A
B
C
FN
Gx
Gy
θ
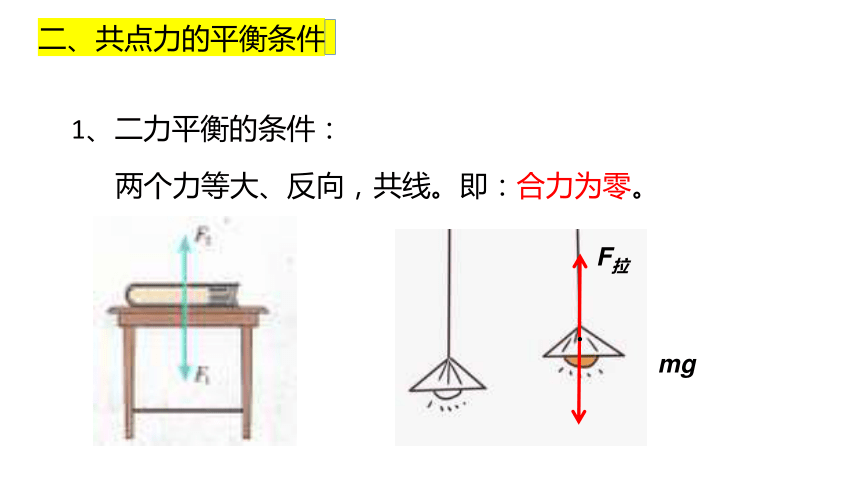
②将G正交分解在沿斜面、垂直斜面两个方向,分别为Gx 和Gy 。因为匀速,平衡态,合力为0,因此x、y两方向上的合力都等于0,则:
应用共点力平衡条件解题的步骤:
①明确研究对象(物体、质点或绳的结点等)。
②对研究对象进行受力分析,并画出受力示意图。
③三个力平衡优先使用矢量三角形解,四个以上建立合适的坐标系,正交分解后列出平衡方程。
④求解方程,并讨论结果。
整体法的选用原则:研究系统外的物体对系统整体的作用力,受力分析时不要再考虑系统内力。适用整体法。
甲乙图中,杆对O点的弹力分别是什么方向?
三、活结绳,死结绳
甲图:水平向右
乙图:斜向上,与竖直方向夹角60°
甲乙两图中,0A绳中的张力多大?
活结绳,结点两端绳中张力大小相同;
死结绳,结点两端绳中张力大小可以不同
G=mg
Tc
Tc
F杆
TA
Tc
F杆
TA
TA=2TC=2mg
TA=TC=mg
活结:能自由滑动;死结:不能自由滑动
bj
四、动态平衡
探究缓慢移动时,力的大小变化问题。
物体缓慢移动时,一些力的大小和方向可能发生变化,但物体物体合力任意时刻仍认为为0。由此,展开分析
动态平衡,力动态分析常用的三个方法
①力的封闭矢量三角形动态分析
②正交分解,列式分析
③矢量三角形之相似三角形
例1.如图所示,小球放在光滑的墙与装有铰链的光滑薄板之间,当墙与薄板之间的夹角θ缓慢地增大到90°的过程中( )
A.小球对墙的压力减小
B.小球对薄板的压力增大
C.小球对墙的压力先减小后增大
D.小球对薄板的压力可能小于球的重力
G
F墙
F杆
分析:缓慢转动杆OA,任意时刻,都是受这三力,且三力合力为0.任意时刻,均可构成封闭的首尾相连的矢量三角形。
由图,可知θ↑,F墙↓,F杆↓
θ
G
F杆
F墙
G
F墙
F杆
F杆y
F杆x
F杆x =F墙
F杆y = G
F杆 sinθ= G
F杆cosθ=F墙
F杆 =
F墙=
θ↑,tanθ↑,sinθ↑,故F杆 ↓F墙↓
如图所示,一不可伸长的轻绳上端悬挂于O点,下端系一小球现对小球施加一水平拉力F,使小球在图示位置保持静止,若保持小球位置不变,将力F方向逆时针缓慢转至与绳垂直的过程中,则( )
A. 力F逐渐增大 B. 力F逐渐减小
C. 力F先减小后增大 D. 力F先增大后减小
建议用矢量三角形的方法,直接、便捷、准确看到力的大小变化以及极值。
也可以用正交分解,列式分析,但极值可能不易分析到位。
(多选)如图所示,在倾角为α的斜面上,放一质量为m的小球,小球和斜面及挡板间均无摩擦,当挡板绕O点逆时针缓慢地转向水平位置的过程中( )
A.斜面对球的支持力逐渐增大
B.斜面对球的支持力逐渐减小
C.挡板对小球的弹力先减小后增大
D.挡板对小球的弹力先增大后减小
如下图所示,质量分别为mA、mB的A、B两个楔形物体叠放在一起,B靠在竖直墙壁上,在力F的作用下,A、B都始终静止不动,则
A.墙壁对B的摩擦力大小为(mA+mB)g
B.A、B之间一定有摩擦力作用
C.力F增大,墙壁对B的摩擦力也增大
D.力F增大,B所受的合外力一定不变
如图所示,倾角为30°的斜面体C质量为4m,放置在粗糙的水平地面上,质量为4m的物块B放置在斜面上,轻绳1一端系在B上,另一端绕过光滑定滑轮与另外两轻绳2、3系于O点,其中轻绳3下端悬挂质量为m的物体A,轻绳2与水平方向的夹角为30°。轻绳1在定滑轮左侧的部分与斜面平行,右侧的部分水平,整个系统处于静止状态,重力加速度为g,下列说法中正确的是
A.B受到的摩擦力沿斜面向下
B.地面对C的支持力大小为8mg
C.地面对C的摩擦力大小为mg
D.若不断增大A的质量,整个系统仍静止,则B受到的摩擦力将逐渐增大
相似三角形法—讲
如图所示,AC是上端带光滑轻质定滑轮的固定竖直杆,质量不计的轻杆BC一端通过铰链固定在C点,另一端B悬挂一重力为G的物体,且B端系有一根轻绳并绕过定滑轮,用力F拉绳,开始时∠BCA>90°,现使∠BCA缓慢变小,直到∠BCA=30°.此过程中,轻杆BC所受的力( )
A.逐渐减小 B.逐渐增大
C.大小不变 D.先减小后增大
如图所示,木板B放置在粗糙水平地面上,O为光滑铰链。轻杆一端与铰链O固定连接,另一端固定连接一质量为m的小球A。现将轻绳一端拴在小球A上,另一端通过光滑的定滑轮由力F牵引,定滑轮位于O的正上方,整个系统处于静止状态。现改变力F的大小使小球A和轻杆从图示位置缓慢运动到正下方,木板始终保持静止,则在整个过程中( )
A. 外力F大小不变
B. 轻杆对小球的作用力大小不变
C. 地面对木板支持力逐渐变小
D. 地面对木板的摩擦力逐渐增大
相似三角形法—讲
练习(受力分析)如右图所示,轻绳一端连接放置在水平地面上的物体Q,另一端绕过固定在天花板上的定滑轮与小球P连接,P、Q始终处于静止状态,则
A.Q可能受到三个力的作用
B.Q一定受到四个力的作用
C.Q受到的轻绳拉力与重力的合力方向水平向左
D.Q受到的轻绳拉力与重力的合力方向指向左下方
变式
如图所示,物体a、b和c叠放在水平桌面上,水平力Fb=5N、Fc=10N分别作用于物体b、c上,a、b和c仍保持静止。以f1、f2、f3分别表示a与b、b与c、c与桌面间的静摩擦力的大小,则( )
A.f1=5N,f2=0、f3=5N
B.f1=5N,f2=5N、f3=0
C.f1=0,f2=5N、f3=5N
D.f1=0,f2=10N、f3=5N
C
用三根细线a、b、c将质量均为m的两个小球连接并悬挂,如图所示。两小球处于静止状态,细线a与竖直方向的夹角为37°,细线c水平,sin37°=0.6,cos37°=0.8,则( )
A.细线a上的拉力为2mg
B.细线c上的拉力为1.5mg
C.细线b上的拉力为mg
D.细线b与竖直方向夹角θ的正切值为
AD
如图在光滑墙壁上用网兜把足球挂在A点,足球与墙壁的接触点为 B。足球的质量为 m,悬绳与墙壁的夹角为 α,网兜的质量不计。求悬绳对足球的拉力和墙壁对足球的支持力
解:①对足球受力分析如图:
G
FN
FT
②足球受三个力平衡,合力为0,三力构成一首尾相连的矢量三角形
α
FN
G
FT
如图所示,重物的质量为m,轻细绳AO和BO的A端、B端是固定的,平衡时AO是水平的,BO与水平方向的夹角为θ,重力加速度为g,AO的拉力F1和BO的拉力F2的大小分别是( )
D
G
Ff
A
B
C
FN
Gx
Gy
θ
共点力的平衡
一、平衡状态
1.定义:物体在几个力作用下保持静止或匀速直线运动的状态,叫平衡状态。
3.v=0,就是静止吗?
不是,静止是一种平衡态,v=0,如竖直上抛最高点,此时仅受重力,不平衡。
缓慢移动,是移动速度无限小,运动中各点处于准“静止”状态,这种状态可视为平衡状态,蕴含着极限思想。
2.处于平衡状态的物体其加速度是多大?
静止、匀速、缓慢移动,加速度a=0
4.“静止”和“v=0”的区别和联系
v=0
合力为0,即a=0时,静止,处于平衡状态
合力不为0,即a≠0时,不静止,非平衡态,如,竖直上抛运动的最高点时刻
1、二力平衡的条件:
二、共点力的平衡条件
两个力等大、反向,共线。即:合力为零。
F拉
mg
·
如果物体受到三个力的作用保持平衡,这三个力什么关系呢?
根据平行四边形定则,求任意两个力的合力,这二力合力与第三力等大反向,它与第三个力平衡;最终把三力平衡问题转化为二力平衡问题。即可得三个力的合力为0。
2、三力平衡的条件:
如果物体受到四个共点力平衡,我们可以两个两个的合成,最终合力为0。
mg
FN
F牵
Ff
3、四力平衡
如果物体受到N个力的作用平衡,我们可以根据平行四边形定则,任意一个力与其余各力的合力大小相等、方向相反、作用在同一条直线上,最终把多力平衡问题转化为二力平衡问题。即物体所受的合力为0。
4、多力平衡
F
F
二、共点力平衡的条件
1.条件:共点力平衡的条件是合力为0。
2.公式:F合=0。
3.由平衡条件得出的三个结论:
【例题】生活中常用一根水平绳拉着悬吊重物的绳索来改变或固定悬吊物的位置。如图悬吊重物的细绳,其O点被一水平绳BO牵引,使悬绳AO段和竖直方向成θ角,若悬吊物所受的重力为G,则悬绳AO和水平绳BO所受的拉力各等于多少?
分析:用几段绳或轻杆连接的问题,我们要对结点受力分析
方法1:矢量三角形法
解析:①结点O受力分析如图:
F1
F2
②结点O静止,三个力的合力为零;三力构成一个首尾相连的矢量三角形
②平移F1和F2后,三个力刚好首尾相接组成一个矢量三角形。
F1
F2
G
θ
方法2:正交分解法
①如图,对结点O受力分析,
解得:F1=G/cosθ,F2=Gtanθ。
F1
F2
F1x
F1y
②将F1正交分解在水平、竖直两个方向,分别为F1x 和F1y 。因为结点合力为0,因此x、y两方向上的合力都等于0,则:
F2 =F1x
F1y = G
F2 = F1sinθ
F1cosθ=G
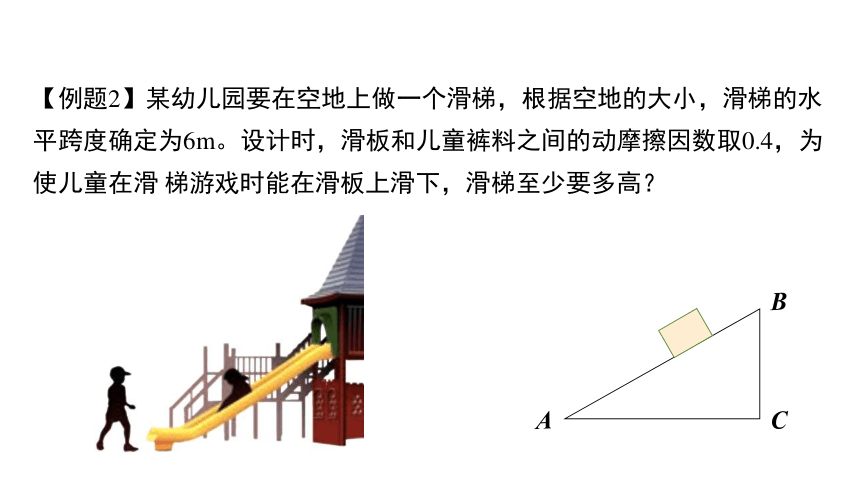
【例题2】某幼儿园要在空地上做一个滑梯,根据空地的大小,滑梯的水平跨度确定为6m。设计时,滑板和儿童裤料之间的动摩擦因数取0.4,为使儿童在滑 梯游戏时能在滑板上滑下,滑梯至少要多高?
A
B
C
解:
①以小孩为研究对象,受力分析
Ff=μFN
由以上各式得: μ=tanθ
由几何关系可得:tanθ
可得:h=μ·AC=0.4×6m=2.4m
G
Ff
A
B
C
FN
Gx
Gy
θ
②将G正交分解在沿斜面、垂直斜面两个方向,分别为Gx 和Gy 。因为匀速,平衡态,合力为0,因此x、y两方向上的合力都等于0,则:
应用共点力平衡条件解题的步骤:
①明确研究对象(物体、质点或绳的结点等)。
②对研究对象进行受力分析,并画出受力示意图。
③三个力平衡优先使用矢量三角形解,四个以上建立合适的坐标系,正交分解后列出平衡方程。
④求解方程,并讨论结果。
整体法的选用原则:研究系统外的物体对系统整体的作用力,受力分析时不要再考虑系统内力。适用整体法。
甲乙图中,杆对O点的弹力分别是什么方向?
三、活结绳,死结绳
甲图:水平向右
乙图:斜向上,与竖直方向夹角60°
甲乙两图中,0A绳中的张力多大?
活结绳,结点两端绳中张力大小相同;
死结绳,结点两端绳中张力大小可以不同
G=mg
Tc
Tc
F杆
TA
Tc
F杆
TA
TA=2TC=2mg
TA=TC=mg
活结:能自由滑动;死结:不能自由滑动
bj
四、动态平衡
探究缓慢移动时,力的大小变化问题。
物体缓慢移动时,一些力的大小和方向可能发生变化,但物体物体合力任意时刻仍认为为0。由此,展开分析
动态平衡,力动态分析常用的三个方法
①力的封闭矢量三角形动态分析
②正交分解,列式分析
③矢量三角形之相似三角形
例1.如图所示,小球放在光滑的墙与装有铰链的光滑薄板之间,当墙与薄板之间的夹角θ缓慢地增大到90°的过程中( )
A.小球对墙的压力减小
B.小球对薄板的压力增大
C.小球对墙的压力先减小后增大
D.小球对薄板的压力可能小于球的重力
G
F墙
F杆
分析:缓慢转动杆OA,任意时刻,都是受这三力,且三力合力为0.任意时刻,均可构成封闭的首尾相连的矢量三角形。
由图,可知θ↑,F墙↓,F杆↓
θ
G
F杆
F墙
G
F墙
F杆
F杆y
F杆x
F杆x =F墙
F杆y = G
F杆 sinθ= G
F杆cosθ=F墙
F杆 =
F墙=
θ↑,tanθ↑,sinθ↑,故F杆 ↓F墙↓
如图所示,一不可伸长的轻绳上端悬挂于O点,下端系一小球现对小球施加一水平拉力F,使小球在图示位置保持静止,若保持小球位置不变,将力F方向逆时针缓慢转至与绳垂直的过程中,则( )
A. 力F逐渐增大 B. 力F逐渐减小
C. 力F先减小后增大 D. 力F先增大后减小
建议用矢量三角形的方法,直接、便捷、准确看到力的大小变化以及极值。
也可以用正交分解,列式分析,但极值可能不易分析到位。
(多选)如图所示,在倾角为α的斜面上,放一质量为m的小球,小球和斜面及挡板间均无摩擦,当挡板绕O点逆时针缓慢地转向水平位置的过程中( )
A.斜面对球的支持力逐渐增大
B.斜面对球的支持力逐渐减小
C.挡板对小球的弹力先减小后增大
D.挡板对小球的弹力先增大后减小
如下图所示,质量分别为mA、mB的A、B两个楔形物体叠放在一起,B靠在竖直墙壁上,在力F的作用下,A、B都始终静止不动,则
A.墙壁对B的摩擦力大小为(mA+mB)g
B.A、B之间一定有摩擦力作用
C.力F增大,墙壁对B的摩擦力也增大
D.力F增大,B所受的合外力一定不变
如图所示,倾角为30°的斜面体C质量为4m,放置在粗糙的水平地面上,质量为4m的物块B放置在斜面上,轻绳1一端系在B上,另一端绕过光滑定滑轮与另外两轻绳2、3系于O点,其中轻绳3下端悬挂质量为m的物体A,轻绳2与水平方向的夹角为30°。轻绳1在定滑轮左侧的部分与斜面平行,右侧的部分水平,整个系统处于静止状态,重力加速度为g,下列说法中正确的是
A.B受到的摩擦力沿斜面向下
B.地面对C的支持力大小为8mg
C.地面对C的摩擦力大小为mg
D.若不断增大A的质量,整个系统仍静止,则B受到的摩擦力将逐渐增大
相似三角形法—讲
如图所示,AC是上端带光滑轻质定滑轮的固定竖直杆,质量不计的轻杆BC一端通过铰链固定在C点,另一端B悬挂一重力为G的物体,且B端系有一根轻绳并绕过定滑轮,用力F拉绳,开始时∠BCA>90°,现使∠BCA缓慢变小,直到∠BCA=30°.此过程中,轻杆BC所受的力( )
A.逐渐减小 B.逐渐增大
C.大小不变 D.先减小后增大
如图所示,木板B放置在粗糙水平地面上,O为光滑铰链。轻杆一端与铰链O固定连接,另一端固定连接一质量为m的小球A。现将轻绳一端拴在小球A上,另一端通过光滑的定滑轮由力F牵引,定滑轮位于O的正上方,整个系统处于静止状态。现改变力F的大小使小球A和轻杆从图示位置缓慢运动到正下方,木板始终保持静止,则在整个过程中( )
A. 外力F大小不变
B. 轻杆对小球的作用力大小不变
C. 地面对木板支持力逐渐变小
D. 地面对木板的摩擦力逐渐增大
相似三角形法—讲
练习(受力分析)如右图所示,轻绳一端连接放置在水平地面上的物体Q,另一端绕过固定在天花板上的定滑轮与小球P连接,P、Q始终处于静止状态,则
A.Q可能受到三个力的作用
B.Q一定受到四个力的作用
C.Q受到的轻绳拉力与重力的合力方向水平向左
D.Q受到的轻绳拉力与重力的合力方向指向左下方
变式
如图所示,物体a、b和c叠放在水平桌面上,水平力Fb=5N、Fc=10N分别作用于物体b、c上,a、b和c仍保持静止。以f1、f2、f3分别表示a与b、b与c、c与桌面间的静摩擦力的大小,则( )
A.f1=5N,f2=0、f3=5N
B.f1=5N,f2=5N、f3=0
C.f1=0,f2=5N、f3=5N
D.f1=0,f2=10N、f3=5N
C
用三根细线a、b、c将质量均为m的两个小球连接并悬挂,如图所示。两小球处于静止状态,细线a与竖直方向的夹角为37°,细线c水平,sin37°=0.6,cos37°=0.8,则( )
A.细线a上的拉力为2mg
B.细线c上的拉力为1.5mg
C.细线b上的拉力为mg
D.细线b与竖直方向夹角θ的正切值为
AD
如图在光滑墙壁上用网兜把足球挂在A点,足球与墙壁的接触点为 B。足球的质量为 m,悬绳与墙壁的夹角为 α,网兜的质量不计。求悬绳对足球的拉力和墙壁对足球的支持力
解:①对足球受力分析如图:
G
FN
FT
②足球受三个力平衡,合力为0,三力构成一首尾相连的矢量三角形
α
FN
G
FT
如图所示,重物的质量为m,轻细绳AO和BO的A端、B端是固定的,平衡时AO是水平的,BO与水平方向的夹角为θ,重力加速度为g,AO的拉力F1和BO的拉力F2的大小分别是( )
D
