4.3 课时2 瞬时加速度及图像问题 课件(共17张PPT) 2024-2025学年高一物理粤教版(2019)必修第一册
文档属性
| 名称 | 4.3 课时2 瞬时加速度及图像问题 课件(共17张PPT) 2024-2025学年高一物理粤教版(2019)必修第一册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 953.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-02 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
4.3 课时2 瞬时加速度及图像问题
physics
一、瞬时加速度(突变)问题
1.两种模型的特点
(1) 轻绳、轻杆、接触面模型:
微小形变,形变恢复几乎不需要时间,弹力可以突变.
(轻绳、轻杆两端和垂直接触面方向加速度大小相等)
(2) 轻弹簧、轻橡皮绳模型:
形变量大,形变恢复需要较长时间,弹力不能突变
(轻弹簧、轻橡皮绳两端加速度大小不一定相等)
2.解决此类问题的基本思路
(1) 分析突变前受力
(2) 分析哪些力能突变
分析突变后受力
两种模型
加速度与合外力具有瞬时对应关系,二者总是同时产生、同时变化、同时消失,当物体所受合外力发生突变时,加速度也随着发生突变,而物体运动的速度不能发生突变.
【例题】如图所示,质量分别为m和2m的A和B两球用轻弹簧连接,A球用细线悬挂起来,两球均处于静止状态,如果将悬挂A球的细线剪断,此时A和B两球的瞬时加速度aA、aB的大小分别是( )
A.aA=0,aB=0 B.aA=g,aB=g
C.aA=3g,aB=g D.aA=3g,aB=0
D
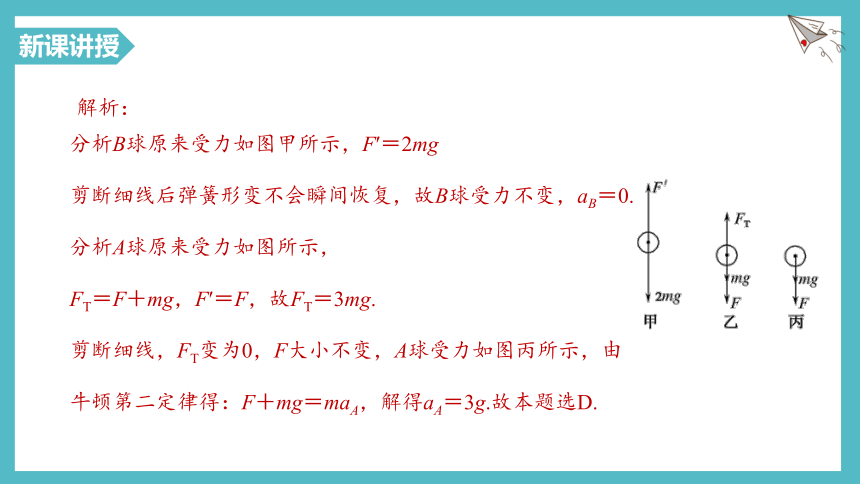
解析:
分析B球原来受力如图甲所示,F′=2mg
剪断细线后弹簧形变不会瞬间恢复,故B球受力不变,aB=0.分析A球原来受力如图所示,
FT=F+mg,F′=F,故FT=3mg.
剪断细线,FT变为0,F大小不变,A球受力如图丙所示,由牛顿第二定律得:F+mg=maA,解得aA=3g.故本题选D.
【例题】如图甲所示,一质量为m的物体系于长度分别为l1、l2的两根细线上,l1的一端悬挂在天花板上,与竖直方向夹角为θ,l2水平拉直,物体处于平衡状态,现将l2线剪断.
(1)求剪断l2瞬间物体的加速度;
(2)若将上图中的细线l1改变为长度相同、质量不计的轻弹簧,如图乙所示,其他条件不变,现将l2剪断,求剪断瞬间物体的加速度.
解析:
(1)由于l1是细线,其物理模型是不可拉伸的刚性绳,当线上的张力变化时,细线的长度形变量忽略不计,因此当剪断l2的瞬间,l2上的张力突然消失,l1线上的张力发生突变,这时物体受力如下左图所示,
FT1=mgcos θ,mgsin θ=ma,解得a=gsin θ.
(2)因l2被剪断的瞬间,弹簧l1上的弹力FT1未发生变化,所以物体所受的合力与FT2等大反向,如下右图所示,由牛顿第二定律,在水平方向有:
mgtan θ=ma,解得a=gtan θ.
解题方法:
①搞清各物体初始状态对地的运动和物体间的相对运动,确定物体间的摩擦力方向;
②分别隔离两物体进行受力分析,准确求出各物体在各个运动过程中的加速度(注意两过程的连接处加速度可能突变);
③找出物体之间的位移(路程)关系或速度关系是解题的突破口.求解中应注意联系两个过程的纽带,即每一个过程的末速度是下一个过程的初速度。
二、动力学图像问题
1、常见的图像形式
在动力学与运动学问题中,常见、常用的图像是位移图像(x-t图像)、速度图像(v-t图像)和力的图像(F-t图像)等,这些图像反映的是物体的运动规律、受力规律,而绝非代表物体的运动轨迹.
(2)特别注意图像中的点、线段、斜率、截距、交点、拐点、面积等方面了解图像给出的信息,再利用共点力平衡、牛顿运动定律及运动学公式解题.
2、解决图像综合问题的关键
(1)把图像与具体的题意、情境结合起来,明确图像的物理意义,明确图像所反映的物理过程.
【例题】一质量为m=1 kg的物体在水平恒力F作用下沿直线水平运动,1 s末撤去恒力F,其v-t图像如图所示,则恒力F和物体所受阻力Ff的大小是( )
A.F=9 N,Ff=2 N B.F=8 N,Ff=3 N
C.F=8 N,Ff=2 N D.F=9 N,Ff=3 N
D
解析:由v-t图像可知,0~1 s内,物体做匀加速直线运动,共加速度大小为a1= = m/s2=6 m/s2;1~3 s内,物体做匀减速直线运动,其加速度的大小为a2= m/s2=3 m/s2.根据牛顿第二定律,0~1 s有F-Ff=ma1,1~3 s有Ff=ma2,解得F=9 N,Ff=3 N.故D正确,A、B、C错误.
【例题】粗糙的水平地面上一物体在水平拉力作用下做直线运动,水平拉力F及运动速度v随时间变化的图像如图甲、乙所示.取重力加速度g=10 m/s2,求:
(1)前2 s内物体运动的加速度和位移大小;
(2)物体的质量m和物体与地面间的动摩擦因数μ.
解析:
(1)由v-t图像可知,前2 s内物体运动的加速度为
a== m/s2=2 m/s2
前2 s内物体运动的位移为x= at2= ×2×22 m=4 m.
(2)物体受力如图所示.对于前2 s,由牛顿第二定律得F1-Ff=ma,其中Ff=μmg
2 s后物体做匀速直线运动,由二力平衡条件得F2=Ff
由F t图像知F1=15 N,F2=5 N
代入数据解得m=5 kg,μ=0.1.
1.如图所示,轻弹簧上端与一质量为m1的木块1相连,下端与另一质量为m2的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2,重力加速度大小为g.则有( )
A.a1=g,a2=g B.a1=0,a2=g
C.a1=0,a2=g D.a1=g,a2= g
C
2.(多选)如图甲所示,一轻弹簧下端固定在水平面上,上端放置一小物体(不粘连),小物体处于静止状态。现对小物体施一竖直向上的拉力F,使小物体向上做匀加速直线运动,拉力F与物体位移x的关系如图乙所示,a、b、c均为已知量,重力加速度为g,弹簧始终在弹性限度内。则下列结论正确的是( )
A.物体与弹簧分离时,弹簧处于原长
B.小物体质量为m=
C.物体的加速度大小为g
D.物体从开始运动到离开弹簧的过程经过的时间为
ABD
4.3 课时2 瞬时加速度及图像问题
physics
一、瞬时加速度(突变)问题
1.两种模型的特点
(1) 轻绳、轻杆、接触面模型:
微小形变,形变恢复几乎不需要时间,弹力可以突变.
(轻绳、轻杆两端和垂直接触面方向加速度大小相等)
(2) 轻弹簧、轻橡皮绳模型:
形变量大,形变恢复需要较长时间,弹力不能突变
(轻弹簧、轻橡皮绳两端加速度大小不一定相等)
2.解决此类问题的基本思路
(1) 分析突变前受力
(2) 分析哪些力能突变
分析突变后受力
两种模型
加速度与合外力具有瞬时对应关系,二者总是同时产生、同时变化、同时消失,当物体所受合外力发生突变时,加速度也随着发生突变,而物体运动的速度不能发生突变.
【例题】如图所示,质量分别为m和2m的A和B两球用轻弹簧连接,A球用细线悬挂起来,两球均处于静止状态,如果将悬挂A球的细线剪断,此时A和B两球的瞬时加速度aA、aB的大小分别是( )
A.aA=0,aB=0 B.aA=g,aB=g
C.aA=3g,aB=g D.aA=3g,aB=0
D
解析:
分析B球原来受力如图甲所示,F′=2mg
剪断细线后弹簧形变不会瞬间恢复,故B球受力不变,aB=0.分析A球原来受力如图所示,
FT=F+mg,F′=F,故FT=3mg.
剪断细线,FT变为0,F大小不变,A球受力如图丙所示,由牛顿第二定律得:F+mg=maA,解得aA=3g.故本题选D.
【例题】如图甲所示,一质量为m的物体系于长度分别为l1、l2的两根细线上,l1的一端悬挂在天花板上,与竖直方向夹角为θ,l2水平拉直,物体处于平衡状态,现将l2线剪断.
(1)求剪断l2瞬间物体的加速度;
(2)若将上图中的细线l1改变为长度相同、质量不计的轻弹簧,如图乙所示,其他条件不变,现将l2剪断,求剪断瞬间物体的加速度.
解析:
(1)由于l1是细线,其物理模型是不可拉伸的刚性绳,当线上的张力变化时,细线的长度形变量忽略不计,因此当剪断l2的瞬间,l2上的张力突然消失,l1线上的张力发生突变,这时物体受力如下左图所示,
FT1=mgcos θ,mgsin θ=ma,解得a=gsin θ.
(2)因l2被剪断的瞬间,弹簧l1上的弹力FT1未发生变化,所以物体所受的合力与FT2等大反向,如下右图所示,由牛顿第二定律,在水平方向有:
mgtan θ=ma,解得a=gtan θ.
解题方法:
①搞清各物体初始状态对地的运动和物体间的相对运动,确定物体间的摩擦力方向;
②分别隔离两物体进行受力分析,准确求出各物体在各个运动过程中的加速度(注意两过程的连接处加速度可能突变);
③找出物体之间的位移(路程)关系或速度关系是解题的突破口.求解中应注意联系两个过程的纽带,即每一个过程的末速度是下一个过程的初速度。
二、动力学图像问题
1、常见的图像形式
在动力学与运动学问题中,常见、常用的图像是位移图像(x-t图像)、速度图像(v-t图像)和力的图像(F-t图像)等,这些图像反映的是物体的运动规律、受力规律,而绝非代表物体的运动轨迹.
(2)特别注意图像中的点、线段、斜率、截距、交点、拐点、面积等方面了解图像给出的信息,再利用共点力平衡、牛顿运动定律及运动学公式解题.
2、解决图像综合问题的关键
(1)把图像与具体的题意、情境结合起来,明确图像的物理意义,明确图像所反映的物理过程.
【例题】一质量为m=1 kg的物体在水平恒力F作用下沿直线水平运动,1 s末撤去恒力F,其v-t图像如图所示,则恒力F和物体所受阻力Ff的大小是( )
A.F=9 N,Ff=2 N B.F=8 N,Ff=3 N
C.F=8 N,Ff=2 N D.F=9 N,Ff=3 N
D
解析:由v-t图像可知,0~1 s内,物体做匀加速直线运动,共加速度大小为a1= = m/s2=6 m/s2;1~3 s内,物体做匀减速直线运动,其加速度的大小为a2= m/s2=3 m/s2.根据牛顿第二定律,0~1 s有F-Ff=ma1,1~3 s有Ff=ma2,解得F=9 N,Ff=3 N.故D正确,A、B、C错误.
【例题】粗糙的水平地面上一物体在水平拉力作用下做直线运动,水平拉力F及运动速度v随时间变化的图像如图甲、乙所示.取重力加速度g=10 m/s2,求:
(1)前2 s内物体运动的加速度和位移大小;
(2)物体的质量m和物体与地面间的动摩擦因数μ.
解析:
(1)由v-t图像可知,前2 s内物体运动的加速度为
a== m/s2=2 m/s2
前2 s内物体运动的位移为x= at2= ×2×22 m=4 m.
(2)物体受力如图所示.对于前2 s,由牛顿第二定律得F1-Ff=ma,其中Ff=μmg
2 s后物体做匀速直线运动,由二力平衡条件得F2=Ff
由F t图像知F1=15 N,F2=5 N
代入数据解得m=5 kg,μ=0.1.
1.如图所示,轻弹簧上端与一质量为m1的木块1相连,下端与另一质量为m2的木块2相连,整个系统置于水平放置的光滑木板上,并处于静止状态.现将木板沿水平方向突然抽出,设抽出后的瞬间,木块1、2的加速度大小分别为a1、a2,重力加速度大小为g.则有( )
A.a1=g,a2=g B.a1=0,a2=g
C.a1=0,a2=g D.a1=g,a2= g
C
2.(多选)如图甲所示,一轻弹簧下端固定在水平面上,上端放置一小物体(不粘连),小物体处于静止状态。现对小物体施一竖直向上的拉力F,使小物体向上做匀加速直线运动,拉力F与物体位移x的关系如图乙所示,a、b、c均为已知量,重力加速度为g,弹簧始终在弹性限度内。则下列结论正确的是( )
A.物体与弹簧分离时,弹簧处于原长
B.小物体质量为m=
C.物体的加速度大小为g
D.物体从开始运动到离开弹簧的过程经过的时间为
ABD
同课章节目录
- 第一章 运动的描述
- 第一节 质点 参考系 时间
- 第二节 位置 位移
- 第三节 速度
- 第四节 测量直线运动物体的瞬时速度
- 第五节 加速度
- 第二章 匀变速直线运动
- 第一节 匀变速直线运动的特点
- 第二节 匀变速直线运动的规律
- 第三节 测量匀变速直线运动的加速度
- 第四节 自由落体运动
- 第五节 匀变速直线运动与汽车安全行驶
- 第三章 相互作用
- 第一节 重力
- 第二节 弹力
- 第三节 摩擦力
- 第四节 力的合成
- 第五节 力的分解
- 第六节 共点力的平衡条件及其应用
- 第四章 牛顿运动定律
- 第一节 牛顿第一定律
- 第二节 加速度与力、质量之间的关系
- 第三节 牛顿第二定律
- 第四节 牛顿第三定律
- 第五节 牛顿运动定律的应用
- 第六节 失重和超重
- 第七节 力学单位
