九年级数学上点拨与精练第24章圆 综合质量检测卷(原卷版+解析版)
文档属性
| 名称 | 九年级数学上点拨与精练第24章圆 综合质量检测卷(原卷版+解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-02 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
九年级数学上点拨与精练
第24章 圆 综合质量检测卷
考试范围:24章;考试时间:120分钟;满分120分
第I卷(选择题)
一、单选题(每小题3分,共30分)
1.如图,点A、B、C在上,若,则的度数为( )
A. B. C. D.
2.下列说法中,正确的是( )
A.长度相等的弧是等弧
B.平分弦的直径垂直于弦
C.三角形外心到三边距离相等
D.不在同一条直线上的三个点确定一个圆
3.用反证法证明“若的周长为16,则较长边的长不小于4”时,应假设( )
A. B. C. D.
4.如图,将三块完全相同的等腰直角三角板的一个锐角顶点都放在点处,再使其各有一条直角边恰好在的边上,此时点是( )
A.的外心 B.的内心
C.的重心 D.的垂心
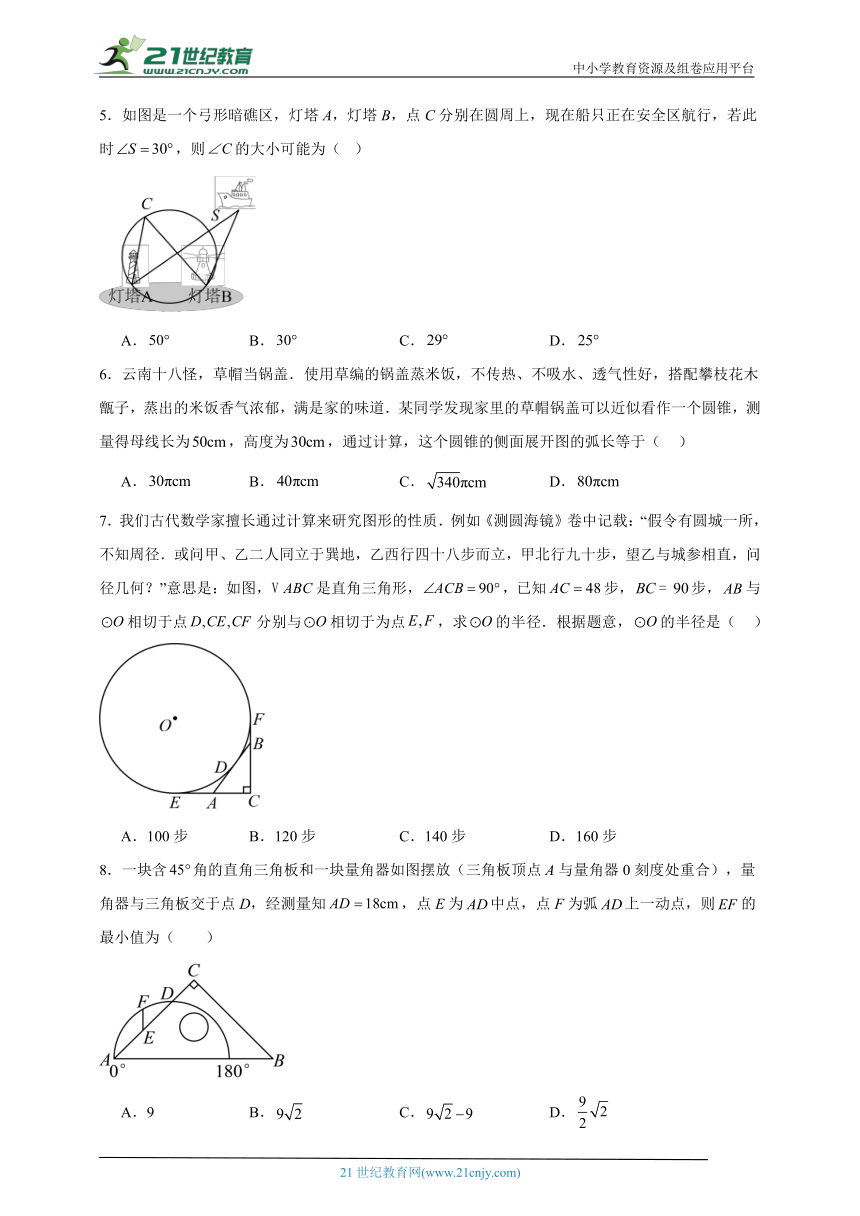
5.如图是一个弓形暗礁区,灯塔A,灯塔B,点C分别在圆周上,现在船只正在安全区航行,若此时,则的大小可能为( )
A. B. C. D.
6.云南十八怪,草帽当锅盖.使用草编的锅盖蒸米饭,不传热、不吸水、透气性好,搭配攀枝花木甑子,蒸出的米饭香气浓郁,满是家的味道.某同学发现家里的草帽锅盖可以近似看作一个圆锥,测量得母线长为,高度为,通过计算,这个圆锥的侧面展开图的弧长等于( )
A. B. C. D.
7.我们古代数学家擅长通过计算来研究图形的性质.例如《测圆海镜》卷中记载:“假令有圆城一所,不知周径.或问甲、乙二人同立于巽地,乙西行四十八步而立,甲北行九十步,望乙与城参相直,问径几何?”意思是:如图,是直角三角形,,已知步,步,与相切于点分别与相切于为点,求的半径.根据题意,的半径是( )
A.100步 B.120步 C.140步 D.160步
8.一块含角的直角三角板和一块量角器如图摆放(三角板顶点A与量角器0刻度处重合),量角器与三角板交于点D,经测量知,点E为中点,点F为弧上一动点,则的最小值为( )
A.9 B. C. D.
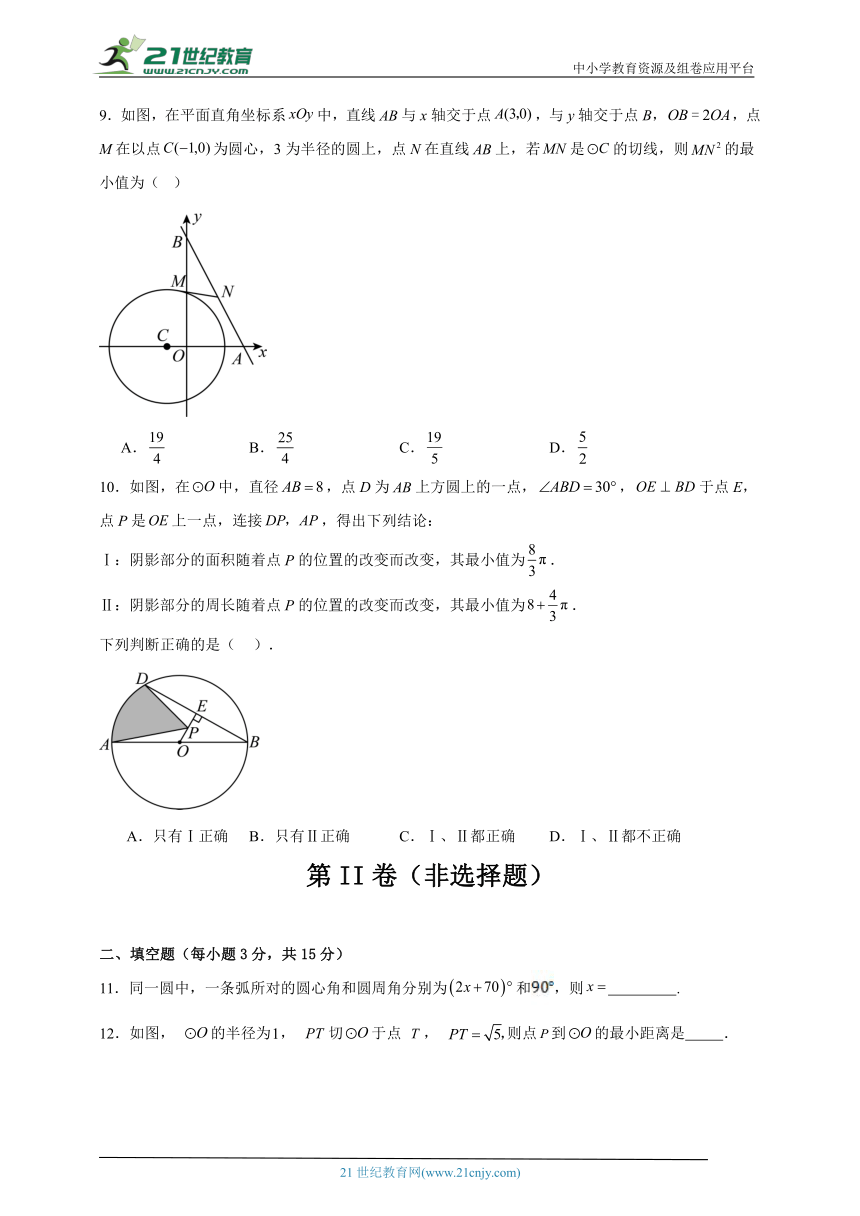
9.如图,在平面直角坐标系中,直线与x轴交于点,与y轴交于点B,,点M在以点为圆心,3为半径的圆上,点N在直线上,若是的切线,则的最小值为( )
A. B. C. D.
10.如图,在中,直径,点D为上方圆上的一点,,于点E,点P是上一点,连接,得出下列结论:
Ⅰ:阴影部分的面积随着点P的位置的改变而改变,其最小值为.
Ⅱ:阴影部分的周长随着点P的位置的改变而改变,其最小值为.
下列判断正确的是( ).
A.只有Ⅰ正确 B.只有Ⅱ正确 C.Ⅰ、Ⅱ都正确 D.Ⅰ、Ⅱ都不正确
第II卷(非选择题)
二、填空题(每小题3分,共15分)
11.同一圆中,一条弧所对的圆心角和圆周角分别为和,则 .
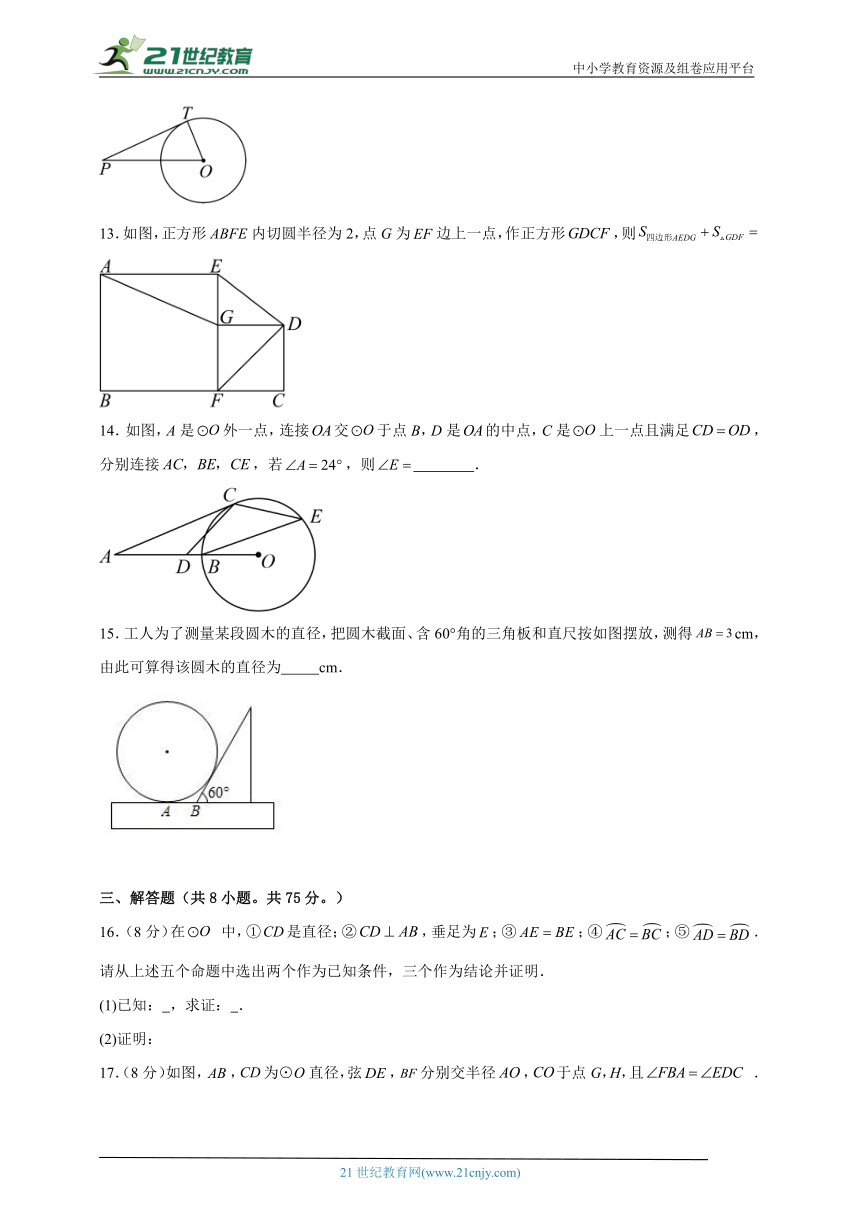
12.如图, 的半径为, 切于点 , 则点到的最小距离是 .
13.如图,正方形内切圆半径为2,点G为边上一点,作正方形,则
14.如图,A是外一点,连接交于点B,D是的中点,C是上一点且满足,分别连接,若,则 .
15.工人为了测量某段圆木的直径,把圆木截面、含60°角的三角板和直尺按如图摆放,测得cm,由此可算得该圆木的直径为 cm.
三、解答题(共8小题。共75分。)
16.(8分)在 中,①是直径;②,垂足为;③;④;⑤.
请从上述五个命题中选出两个作为已知条件,三个作为结论并证明.
(1)已知: ,求证: .
(2)证明:
17.(8分)如图,,为⊙O直径,弦,分别交半径,于点G,H,且 .
(1)求证: .
(2)若,且,求的度数.
18.(10分)利用素材解决:《桥梁的设计》
某地欲修建一座拱桥,桥的底部两端间的水面宽,称跨度,桥面最高点到的距离称拱高,拱桥的轮廓可以设计成是圆弧型或抛物线型,若修建拱桥的跨度米,拱高米.
方案一 方案二
圆弧型 抛物线型
设计成圆弧型,求该圆弧所在圆的半径. 设计成抛物线型,以AB所在直线为x轴,AB的垂直平分线为y轴建立坐标系,求桥拱的函数表达式.
如图,一艘货船露出水面部分的横截面为矩形,测得米,米.请你通过计算说明货船能否分别顺利通过这两座桥梁.
19.(8分)在等腰中,,过A,B两点的⊙O交射线于点D.
(1)如图1,已知,若点O在上,过点D作⊙O的切线交射线于点E,求的度数.
(2)如图2,已知.与交于点F,过点D作,交射线于点E.求证:是⊙O的切线.
20.(9分)阅读与思考
如图是小宇同学的数学日记,请仔细阅读,并完成相应的任务.
×年×月×日星期日作三角形的高线已知:如图1,.求作:的高线.今天,我们组的小明和小红的作法和我不同.小明:如图2,①作线段的垂直平分线找到线段的中点O;②以点O为圆心,的长为半径作圆;③延长交于点D;③连接.则线段就是的高线。小红:如图3,①以点B为圆心,的长为半径作弧;②以点C为圆心,的长为半径作弧,两弧交于点E;③作射线,延长与相交于点D.则线段就是的高线.我有如下思考:以上两种办法依据的数学原理是什么呢?
任务:
(1)填空:小明的作法依据的一个数学定理是______;
(2)根据小红的操作过程,求证:是的高线;
(3)在图2中,若延长线段交于点E,,,,请你直接写出的长.
21.(8分)已知四边形内接于,.
(1)如图1,连接,若的半径为6,,求的长;
(2)如图2,连接,若,,对角线平分,求的长.
22.(12分)如图,是等边的外接圆,P点是劣弧上的一个动点(不与点A,B 重合).
(1)求的度数;
(2)若,,求的长;
(3)若,点P在劣弧上运动的过程中,
①的值是否为定值,若是,请求出这个定值;若不是,求出其值的取值范围.
②试探究的值是否为定值,若是,请求出这个定值;若不 是,求出其的取值范围.
23.(12分)综合与实践
问题情境:小华发现这么一类四边形,有一组对角之和为直角的四边形,小华将这类四边形命名为对余四边形.
猜想证明:
(1)若四边形是对余四边形,则与的度数之和为__________.
(2)如图1,在上有A,B,C三点,是的直径,,相交于点D.四边形是对余四边形吗?若是,请给出证明;若不是,请说明理由,拓展探究:
(3)如图2,在对余四边形中,,,,则线段和之间有怎样的数量关系?请给出你的猜想,并说明理由.
九年级数学上点拨与精练
第24章 圆 综合质量检测卷
考试范围:24章;考试时间:120分钟;满分120分
第I卷(选择题)
一、单选题(每小题3分,共30分)
1.如图,点A、B、C在上,若,则的度数为( )
A. B. C. D.
【答案】D
【分析】本题主要考查了圆周角定理,同圆或等圆中,同弧所对的圆周角度数是圆心角度数的一半,据此可得答案.
【详解】解:∵点A、B、C在上,,
∴,
故选:D.
2.下列说法中,正确的是( )
A.长度相等的弧是等弧
B.平分弦的直径垂直于弦
C.三角形外心到三边距离相等
D.不在同一条直线上的三个点确定一个圆
【答案】D
【分析】根据圆的认识,垂径定理,三角形的内心与外心,确定圆的条件逐项判断即可.
【详解】解:A、在同圆或等圆中,能够完全重合的弧是等弧,故本选项说法错误,不符合题意;
B、平分不是直径的弦的直径垂直于弦,故本选项说法错误,不符合题意;
C、三角形外心到三个顶点的距离相等,故本选项说法错误,不符合题意;
D、不在同一条直线上的三个点确定一个圆,故本选项说法正确,符合题意.
故选:D.
【点睛】本题考查圆的认识,垂径定理,三角形的内心与外心,确定圆的条件.熟练掌握这些数学概念的解题的关键.
3.用反证法证明“若的周长为16,则较长边的长不小于4”时,应假设( )
A. B. C. D.
【答案】C
【分析】本题主要考查的是反证法.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.反证法的步骤中,第一步是假设结论不成立,反面成立.
【详解】解:用反证法证明:“若的周长为16,则较长边的长不小于4”,
则应先假设,
故选:C.
4.如图,将三块完全相同的等腰直角三角板的一个锐角顶点都放在点处,再使其各有一条直角边恰好在的边上,此时点是( )
A.的外心 B.的内心
C.的重心 D.的垂心
【答案】B
【分析】本题考查三角形内接圆,三角形内心的性质:三角形的内心到三角形三边的距离相等,由点M到的距离相等,从而确定点M是的内心.
【详解】解:根据题意可得:点M到的距离相等,都为等腰直角三角形的腰长,
点M是的内心.
故选:B.
5.如图是一个弓形暗礁区,灯塔A,灯塔B,点C分别在圆周上,现在船只正在安全区航行,若此时,则的大小可能为( )
A. B. C. D.
【答案】A
【分析】本题考查了圆周角定理,三角形外角的性质,设与圆相交于D,连接,根据圆周角定理得出,根据三角形外角的性质得出,即可求解.
【详解】解:如图,设与圆相交于D,连接,
∴,
∵,
∴,
∴选项A符合题意,
故选:A.
6.云南十八怪,草帽当锅盖.使用草编的锅盖蒸米饭,不传热、不吸水、透气性好,搭配攀枝花木甑子,蒸出的米饭香气浓郁,满是家的味道.某同学发现家里的草帽锅盖可以近似看作一个圆锥,测量得母线长为,高度为,通过计算,这个圆锥的侧面展开图的弧长等于( )
A. B. C. D.
【答案】D
【分析】此题考查了圆锥的底面圆锥的周长等于展开的扇形的弧长,勾股定理,
首先根据勾股定理求出底面圆的半径,然后求出底面圆的周长,进而可得到圆锥的侧面展开图的弧长.
【详解】∵母线长为,高度为,
∴底面圆的半径为,
∴底面圆的周长为,
∴这个圆锥的侧面展开图的弧长等于.
故选:D.
7.我们古代数学家擅长通过计算来研究图形的性质.例如《测圆海镜》卷中记载:“假令有圆城一所,不知周径.或问甲、乙二人同立于巽地,乙西行四十八步而立,甲北行九十步,望乙与城参相直,问径几何?”意思是:如图,是直角三角形,,已知步,步,与相切于点分别与相切于为点,求的半径.根据题意,的半径是( )
A.100步 B.120步 C.140步 D.160步
【答案】B
【分析】此题考查了切线的性质,正方形的性质和判定,勾股定理等知识,解题的关键是学会利用参数构建方程解决问题.
如图所示,连接,,,证明四边形是正方形,设步,根据切线长定理,得到步,步,利用勾股定理求出,然后构建方程求解即可.
【详解】如图所示,连接,,,
∵,是的切线
∴,
∴
∵
∴四边形是矩形
∵
∴四边形是正方形
设步,则步,步,
∵,,是的切线
∴步,步,
∵步,
∴
∴
∴.
故选:B.
8.一块含角的直角三角板和一块量角器如图摆放(三角板顶点A与量角器0刻度处重合),量角器与三角板交于点D,经测量知,点E为中点,点F为弧上一动点,则的最小值为( )
A.9 B. C. D.
【答案】C
【分析】本题考查点到圆上的最值问题,等腰三角形的判定与性质,勾股定理及垂径定理,设量角器刻度处为点G,为半圆的直径,设的中点为O,则点O为圆心,连接,证明为等腰直角三角形,由当点O,E,F在一条直线上时,取得最小值,即可解答.
【详解】解:设量角器刻度处为点G,如图,
则为半圆的直径,设的中点为O,则点O为圆心,连接,
∵点E为中点,
∴,,
∵,
∴为等腰直角三角形,
∴,
∴,
∵点F为弧上一动点,
∴当点O,E,F在一条直线上时,取得最小值.
∴的最小值为.
故选:C.
9.如图,在平面直角坐标系中,直线与x轴交于点,与y轴交于点B,,点M在以点为圆心,3为半径的圆上,点N在直线上,若是的切线,则的最小值为( )
A. B. C. D.
【答案】C
【分析】本题主要考查切线的性质,坐标与图形,勾股定理等知识,连接由点A的坐标可求出由得,由是的切线知,由勾股定理得,因为所以当最小时最小,即时最小,运用等积法求出,代入可得结论.
【详解】解:连接如图,
∵,
∴,
∵,
∴;
∴;
∵是的切线,
∴,
∴
∵,
∴当最小时最小,即时最小,
∵
,
又
∴,
∴,
故选:C
10.如图,在中,直径,点D为上方圆上的一点,,于点E,点P是上一点,连接,得出下列结论:
Ⅰ:阴影部分的面积随着点P的位置的改变而改变,其最小值为.
Ⅱ:阴影部分的周长随着点P的位置的改变而改变,其最小值为.
下列判断正确的是( ).
A.只有Ⅰ正确 B.只有Ⅱ正确 C.Ⅰ、Ⅱ都正确 D.Ⅰ、Ⅱ都不正确
【答案】B
【分析】此题考查了扇形面积和弧长、垂径定理、圆周角定理等知识,连接,证明,得到阴影部分的面积为,即可判断Ⅰ;证明当三点共线时,取得最小值,最小值为的长度,即为8,得到阴影部分的周长的最小值为,即可判断Ⅱ.
【详解】解:连接,
∵,
∴,
∵,
∴是等边三角形,
∴,
∵,
∴是等腰三角形,
∵于点E,
∴,
∴,
∴,
∴,
∴阴影部分的面积为
∴阴影部分的面积随着点P的位置的改变而不改变,其值为.
故Ⅰ错误;
∵垂直平分,
∴点D与点B关于对称,
∴,
当三点共线时,取得最小值,最小值为的长度,即为8,
∴阴影部分的周长的最小值为,
∴阴影部分的周长随着点P的位置的改变而改变,其最小值为.
故Ⅱ正确;
故选:B
第II卷(非选择题)
二、填空题(每小题3分,共15分)
11.同一圆中,一条弧所对的圆心角和圆周角分别为和,则 .
【答案】55
【分析】此题考查了圆周角定理.注意掌握掌握一条弧所对的圆心角是圆周角的倍是解题的关键.
【详解】解:由圆周角定理知,,
解得.
故答案为:.
12.如图, 的半径为, 切于点 , 则点到的最小距离是 .
【答案】/
【分析】本题考查了切线的性质,勾股定理,根据勾股定理求得的长,进而根据点到圆的最小距离为,即可求解.
【详解】解:∵切于点 ,
∴,
在中,
∴
∴点到的最小距离是,
故答案为:.
13.如图,正方形内切圆半径为2,点G为边上一点,作正方形,则
【答案】8
【分析】本题考查了正方形的性质,内切圆的性质,根据正方形内切圆半径为2,得出,结合,再代入数值进行计算,即可作答.
【详解】解:依题意,
∵正方形内切圆半径为2
∴
∵四边形是正方形
∴
则
故答案为:8
14.如图,A是外一点,连接交于点B,D是的中点,C是上一点且满足,分别连接,若,则 .
【答案】/度
【分析】此题考查了圆周角定理、等边对等角、三角形内角和定理等知识,先证明,再求出,根据圆周角定理即可得到答案.
【详解】解:连接,
∵D是的中点,
∴,
∵
∴
∴
∴,
∴,
∴
故答案为:
15.工人为了测量某段圆木的直径,把圆木截面、含60°角的三角板和直尺按如图摆放,测得cm,由此可算得该圆木的直径为 cm.
【答案】
【分析】如图,切三角板的斜边于点,连接、,利用邻补角计算出,再根据切线长定理和切线的性质得到平分,,所以,,然后利用含30度角的直角三角形三边的关系得到的长,从而得到圆的直径.
【详解】解:如图,切三角板的斜边于点,连接、,则,
与三角板和直尺相切,
平分,,
,,
在中,
,
cm,
该圆木的直径为cm.
故答案为:.
【点睛】本题考查了切线的性质及切线长定理,熟练掌握切线的性质及切线长定理是解题的关键.
三、解答题(共8小题。共75分。)
16.(8分)在 中,①是直径;②,垂足为;③;④;⑤.
请从上述五个命题中选出两个作为已知条件,三个作为结论并证明.
(1)已知: ,求证: .
(2)证明:
【答案】(1)①②;③④⑤
(2)证明过程见详解
【分析】(1)已知,① 是直径 ;② ,垂足为,求证③ ;④;⑤ ,是证明垂径定理的性质;
(2)如图所示(见详解),连接,可得等腰直角三角形,,由三角形全等即可求证.
【详解】(1)解:根据是直径 ,,垂足为,可证明;;成立,是垂径定理的性质,
∴已知是直径 ,,垂足为,求证;;.
(2)解:如图所示,
是直径 ,,垂足为,连接,,
∵,是半径,,
∴,,,
∴,
∴;
∵,
∴,则,
∴,,同圆中,等角所对的弧相等.
【点睛】本题主要考查圆的垂径定理的性质的证明,掌握圆中直径、半径、弦的位置关系,圆心角与所对弧的关系是解题的关键.
17.(8分)如图,,为⊙O直径,弦,分别交半径,于点G,H,且 .
(1)求证: .
(2)若,且,求的度数.
【答案】(1)见解析
(2)108°
【分析】(1)连接,,根据圆周角定理得出,根据直角三角形的性质得到,根据弧、圆周角关系得出,进而得到,则,根据弧、弦的关系即可得解;
(2)根据等腰三角形的性质、三角形内角和定理、圆周角定理推出,根据弧、圆周角的关系得出,即,求出,根据三角形内角和定理、对顶角性质求解即可.
【详解】(1)证明:如图,连接,
∵为⊙O直径,
∴,
∴,
∵,
∴,
∴,
∵∠FBA=∠EDC,
∴,
∴,
即,
∴,
即,
∴;
(2))解:如图,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵为⊙O直径,
∴度数之和为:,
∴,
∴,
∴,
∴,
∴,
∴ ,
∴的度数为108°.
【点睛】本题考查圆周角定理,等弧,等弦,等角.熟练掌握圆周角定理,以及等弧,等弦,等角是解题的关键.同时考查了等腰三角形的性质,三角形的内角和定理以及外角的性质.
18.(10分)利用素材解决:《桥梁的设计》
某地欲修建一座拱桥,桥的底部两端间的水面宽,称跨度,桥面最高点到的距离称拱高,拱桥的轮廓可以设计成是圆弧型或抛物线型,若修建拱桥的跨度米,拱高米.
方案一 方案二
圆弧型 抛物线型
设计成圆弧型,求该圆弧所在圆的半径. 设计成抛物线型,以AB所在直线为x轴,AB的垂直平分线为y轴建立坐标系,求桥拱的函数表达式.
如图,一艘货船露出水面部分的横截面为矩形,测得米,米.请你通过计算说明货船能否分别顺利通过这两座桥梁.
【答案】任务一:方案一,米;方案二,
任务二:方案一,能通过;方案二,不能通过
【分析】本题考查了二次函数的实际应用,垂径定理,勾股定理的应用,掌握建模的数学思想是解题关键.任务一:方案一,设圆的半径为米,根据即可求解;方案二,设桥拱的函数解析式为,将代入即可求解;任务二:方案一,根据即可判断;方案二,当H点的横坐标时,计算其纵坐标即可判断.
【详解】解:任务一
方案一,设圆的半径为米,
在中,,
(米)
方案二,∵顶点C坐标为,
设桥拱的函数解析式为
代入得,.
函数解析式为.
任务二
方案一,如图,由上得,
在中,
.
能通过
方案二,如图建立直角坐标系,
当H点的横坐标时,,
不能通过.
19.(8分)在等腰中,,过A,B两点的⊙O交射线于点D.
(1)如图1,已知,若点O在上,过点D作⊙O的切线交射线于点E,求的度数.
(2)如图2,已知.与交于点F,过点D作,交射线于点E.求证:是⊙O的切线.
【答案】(1)45°;(2)证明见解析
【分析】(1)利用半径相等以及等边对等角求得,利用切线的性质求得,再根据三角形内角和定理即可求解;
(2)利用圆周角定理求得,利用平行线的性质求得,即可证明是⊙O的切线.
【详解】(1)连接,,
∵,,
∴∠ABC=∠ACB=,∠ABO=∠BAO=,
∴,
∵是切线,
∴,
∴,
在中,;
(2)连接,
∴.
∵,
∴,
∴,
∴是的切线.
【点睛】本题考查了切线的判定和性质,三角形内角和定理,等腰三角形的性质,正确的识别图形是解题的关键.
20.(9分)阅读与思考
如图是小宇同学的数学日记,请仔细阅读,并完成相应的任务.
×年×月×日星期日作三角形的高线已知:如图1,.求作:的高线.今天,我们组的小明和小红的作法和我不同.小明:如图2,①作线段的垂直平分线找到线段的中点O;②以点O为圆心,的长为半径作圆;③延长交于点D;③连接.则线段就是的高线。小红:如图3,①以点B为圆心,的长为半径作弧;②以点C为圆心,的长为半径作弧,两弧交于点E;③作射线,延长与相交于点D.则线段就是的高线.我有如下思考:以上两种办法依据的数学原理是什么呢?
任务:
(1)填空:小明的作法依据的一个数学定理是______;
(2)根据小红的操作过程,求证:是的高线;
(3)在图2中,若延长线段交于点E,,,,请你直接写出的长.
【答案】(1)直径所对的圆周角是直角;
(2)见解析
(3)
【分析】(1)根据作图,结合直径所对的圆周角是直角即可作答;
(2)根据作图,证明是线段的垂直平分线即可作答;
(3)连接、,先求出,,即有,即可得半径,根据弧长公式,问题得解.
【详解】(1)解:根据作图可知:线段是的直径,
即,即有,
则是的高线,
故作法依据的一个数学定理是直径所对的圆周角是直角;
(2)连接,,如图
由作图过程可知:,,
∴点B,点C都在的垂直平分线上,
∴是的垂直平分线,即,
∴是的高线;
(3)连接、,如图,
∵,,
∴,,
∵,,
∴,
∴,
∴半径,
∴.
【点睛】本题考查了圆周角定理,求解弧长以及垂直平分线的判定与性质等知识,掌握圆周角定理是解答本题的关键.
21.(8分)已知四边形内接于,.
(1)如图1,连接,若的半径为6,,求的长;
(2)如图2,连接,若,,对角线平分,求的长.
【答案】(1)
(2)AC
【分析】(1)由90度的圆周角所对的弦是直径得到是直径,则,再利用勾股定理求解即可;
(2)如图2,连接,作于H,先利用勾股定理得到,再由角平分线的定义得到,则可证明,求出,由勾股定理可得. 再证明是等腰直角三角形,同理可得.在中,,据此可得答案.
【详解】(1)解:,
是直径,
∵的半径为6,
.
在中,由勾股定理,得,
∵
∴,
;
(2)解:如图2,连接,作于H,
,,,
.
平分,
,
,
.
四边形内接于,,
,
在中,由根据勾股定理,得,
∴,
∴.
,
∴是等腰直角三角形,
同理可得.
在中,,
.
【点睛】本题主要考查了弧与圆周角之间的关系,90度的圆周角所对的弦是直径,勾股定理,等腰直角三角形的性质与判定,圆内接四边形的性质等等,熟知90度的圆周角所对的弦是直径是解题的关键.
22.(12分)如图,是等边的外接圆,P点是劣弧上的一个动点(不与点A,B 重合).
(1)求的度数;
(2)若,,求的长;
(3)若,点P在劣弧上运动的过程中,
①的值是否为定值,若是,请求出这个定值;若不是,求出其值的取值范围.
②试探究的值是否为定值,若是,请求出这个定值;若不 是,求出其的取值范围.
【答案】(1)
(2)7
(3)①;②的值是定值96.
【分析】(1)首先由等边三角形的性质得到,然后根据圆内接四边形的性质求解即可;
(2)延长到点F使,首先证明出是等边三角形,求出,然后证明出,即可得到;
(3)①首先由(2)可得,,然后得到当点P和点A或点B重合时,的最小值为;当点P,O,C三点共线时,有最大值,然后画出图形,根据勾股定理求解即可;
②延长到点F使,过点A作,由(2)得,是等边三角形,得到,然后根据勾股定理求出,进一步得到,然后结合,代入得到,即可求解.
【详解】(1)解:∵是等边三角形
∴
∵四边形内接于
∴;
(2)如图所示,延长到点F使,
∵
∴
∵
∴是等边三角形
∴,,
∴
∵
∴
∵
∴
∴在和中
∴
∴;
(3)①由(2)可得,
∵点P在劣弧上运动
∴当点P和点A或点B重合时,的长度最小,即或的长度
∵是等边三角形
∴
∴的最小值为
∴的最小值为;
当点P,O,C三点共线时,的长度最大,如图所示,
∴此时是的直径
∴
∵
∴
∴
∴
∵
∴
∴,负值舍去
∴的最大值为8
∴的最大值为8;
∴的值的取值范围是;
②如图所示,延长到点F使,过点A作
由(2)得,是等边三角形
∴
∴,
∴
∵
∴
∴
又∵
∴
.
∴的值是定值96.
【点睛】此题考查了圆与三角形综合题,考查了圆周角定理,等边三角形的性质,圆内接四边形的性质,勾股定理和全等三角形等知识,解题的关键是正确作出辅助线构造等边三角形.
23.(12分)综合与实践
问题情境:小华发现这么一类四边形,有一组对角之和为直角的四边形,小华将这类四边形命名为对余四边形.
猜想证明:
(1)若四边形是对余四边形,则与的度数之和为__________.
(2)如图1,在上有A,B,C三点,是的直径,,相交于点D.四边形是对余四边形吗?若是,请给出证明;若不是,请说明理由,拓展探究:
(3)如图2,在对余四边形中,,,,则线段和之间有怎样的数量关系?请给出你的猜想,并说明理由.
【答案】(1)或;
(2)是,证明见详解;
(3),理由见详解.
【分析】(1)对余四边形的定义即可得出结果;
(2)根据对余四边形的定义,由圆周角定理得出,说明即可;
(3)将绕着点B逆时针旋转得到,连接,利用已知条件得出,利用勾股定理可得结论.
【详解】(1)解:∵四边形是对余四边形,
或
时,.
∴或.
故答案为或.
(2)
证明:是的直径,点A,B,C在上,
.
即.
∴四边形是对余四边形.
(3)猜想:线段和之间的数量关系为:.理由如下:
,
∴将绕着点B逆时针旋转得到,连接,如图,
则,.
.
为等边三角形.
.
,
.
∴∠BFA+∠ADB=30°.
,
.
.
.
.
.
【点睛】本题是圆的综合题,主要考查了对余四边形的定义、圆周角定理、旋转的性质、等边三角形的判定与性质、三角形内角和定理、勾股定理等知识;熟练掌握对余四边形的定义和旋转的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学上点拨与精练
第24章 圆 综合质量检测卷
考试范围:24章;考试时间:120分钟;满分120分
第I卷(选择题)
一、单选题(每小题3分,共30分)
1.如图,点A、B、C在上,若,则的度数为( )
A. B. C. D.
2.下列说法中,正确的是( )
A.长度相等的弧是等弧
B.平分弦的直径垂直于弦
C.三角形外心到三边距离相等
D.不在同一条直线上的三个点确定一个圆
3.用反证法证明“若的周长为16,则较长边的长不小于4”时,应假设( )
A. B. C. D.
4.如图,将三块完全相同的等腰直角三角板的一个锐角顶点都放在点处,再使其各有一条直角边恰好在的边上,此时点是( )
A.的外心 B.的内心
C.的重心 D.的垂心
5.如图是一个弓形暗礁区,灯塔A,灯塔B,点C分别在圆周上,现在船只正在安全区航行,若此时,则的大小可能为( )
A. B. C. D.
6.云南十八怪,草帽当锅盖.使用草编的锅盖蒸米饭,不传热、不吸水、透气性好,搭配攀枝花木甑子,蒸出的米饭香气浓郁,满是家的味道.某同学发现家里的草帽锅盖可以近似看作一个圆锥,测量得母线长为,高度为,通过计算,这个圆锥的侧面展开图的弧长等于( )
A. B. C. D.
7.我们古代数学家擅长通过计算来研究图形的性质.例如《测圆海镜》卷中记载:“假令有圆城一所,不知周径.或问甲、乙二人同立于巽地,乙西行四十八步而立,甲北行九十步,望乙与城参相直,问径几何?”意思是:如图,是直角三角形,,已知步,步,与相切于点分别与相切于为点,求的半径.根据题意,的半径是( )
A.100步 B.120步 C.140步 D.160步
8.一块含角的直角三角板和一块量角器如图摆放(三角板顶点A与量角器0刻度处重合),量角器与三角板交于点D,经测量知,点E为中点,点F为弧上一动点,则的最小值为( )
A.9 B. C. D.
9.如图,在平面直角坐标系中,直线与x轴交于点,与y轴交于点B,,点M在以点为圆心,3为半径的圆上,点N在直线上,若是的切线,则的最小值为( )
A. B. C. D.
10.如图,在中,直径,点D为上方圆上的一点,,于点E,点P是上一点,连接,得出下列结论:
Ⅰ:阴影部分的面积随着点P的位置的改变而改变,其最小值为.
Ⅱ:阴影部分的周长随着点P的位置的改变而改变,其最小值为.
下列判断正确的是( ).
A.只有Ⅰ正确 B.只有Ⅱ正确 C.Ⅰ、Ⅱ都正确 D.Ⅰ、Ⅱ都不正确
第II卷(非选择题)
二、填空题(每小题3分,共15分)
11.同一圆中,一条弧所对的圆心角和圆周角分别为和,则 .
12.如图, 的半径为, 切于点 , 则点到的最小距离是 .
13.如图,正方形内切圆半径为2,点G为边上一点,作正方形,则
14.如图,A是外一点,连接交于点B,D是的中点,C是上一点且满足,分别连接,若,则 .
15.工人为了测量某段圆木的直径,把圆木截面、含60°角的三角板和直尺按如图摆放,测得cm,由此可算得该圆木的直径为 cm.
三、解答题(共8小题。共75分。)
16.(8分)在 中,①是直径;②,垂足为;③;④;⑤.
请从上述五个命题中选出两个作为已知条件,三个作为结论并证明.
(1)已知: ,求证: .
(2)证明:
17.(8分)如图,,为⊙O直径,弦,分别交半径,于点G,H,且 .
(1)求证: .
(2)若,且,求的度数.
18.(10分)利用素材解决:《桥梁的设计》
某地欲修建一座拱桥,桥的底部两端间的水面宽,称跨度,桥面最高点到的距离称拱高,拱桥的轮廓可以设计成是圆弧型或抛物线型,若修建拱桥的跨度米,拱高米.
方案一 方案二
圆弧型 抛物线型
设计成圆弧型,求该圆弧所在圆的半径. 设计成抛物线型,以AB所在直线为x轴,AB的垂直平分线为y轴建立坐标系,求桥拱的函数表达式.
如图,一艘货船露出水面部分的横截面为矩形,测得米,米.请你通过计算说明货船能否分别顺利通过这两座桥梁.
19.(8分)在等腰中,,过A,B两点的⊙O交射线于点D.
(1)如图1,已知,若点O在上,过点D作⊙O的切线交射线于点E,求的度数.
(2)如图2,已知.与交于点F,过点D作,交射线于点E.求证:是⊙O的切线.
20.(9分)阅读与思考
如图是小宇同学的数学日记,请仔细阅读,并完成相应的任务.
×年×月×日星期日作三角形的高线已知:如图1,.求作:的高线.今天,我们组的小明和小红的作法和我不同.小明:如图2,①作线段的垂直平分线找到线段的中点O;②以点O为圆心,的长为半径作圆;③延长交于点D;③连接.则线段就是的高线。小红:如图3,①以点B为圆心,的长为半径作弧;②以点C为圆心,的长为半径作弧,两弧交于点E;③作射线,延长与相交于点D.则线段就是的高线.我有如下思考:以上两种办法依据的数学原理是什么呢?
任务:
(1)填空:小明的作法依据的一个数学定理是______;
(2)根据小红的操作过程,求证:是的高线;
(3)在图2中,若延长线段交于点E,,,,请你直接写出的长.
21.(8分)已知四边形内接于,.
(1)如图1,连接,若的半径为6,,求的长;
(2)如图2,连接,若,,对角线平分,求的长.
22.(12分)如图,是等边的外接圆,P点是劣弧上的一个动点(不与点A,B 重合).
(1)求的度数;
(2)若,,求的长;
(3)若,点P在劣弧上运动的过程中,
①的值是否为定值,若是,请求出这个定值;若不是,求出其值的取值范围.
②试探究的值是否为定值,若是,请求出这个定值;若不 是,求出其的取值范围.
23.(12分)综合与实践
问题情境:小华发现这么一类四边形,有一组对角之和为直角的四边形,小华将这类四边形命名为对余四边形.
猜想证明:
(1)若四边形是对余四边形,则与的度数之和为__________.
(2)如图1,在上有A,B,C三点,是的直径,,相交于点D.四边形是对余四边形吗?若是,请给出证明;若不是,请说明理由,拓展探究:
(3)如图2,在对余四边形中,,,,则线段和之间有怎样的数量关系?请给出你的猜想,并说明理由.
九年级数学上点拨与精练
第24章 圆 综合质量检测卷
考试范围:24章;考试时间:120分钟;满分120分
第I卷(选择题)
一、单选题(每小题3分,共30分)
1.如图,点A、B、C在上,若,则的度数为( )
A. B. C. D.
【答案】D
【分析】本题主要考查了圆周角定理,同圆或等圆中,同弧所对的圆周角度数是圆心角度数的一半,据此可得答案.
【详解】解:∵点A、B、C在上,,
∴,
故选:D.
2.下列说法中,正确的是( )
A.长度相等的弧是等弧
B.平分弦的直径垂直于弦
C.三角形外心到三边距离相等
D.不在同一条直线上的三个点确定一个圆
【答案】D
【分析】根据圆的认识,垂径定理,三角形的内心与外心,确定圆的条件逐项判断即可.
【详解】解:A、在同圆或等圆中,能够完全重合的弧是等弧,故本选项说法错误,不符合题意;
B、平分不是直径的弦的直径垂直于弦,故本选项说法错误,不符合题意;
C、三角形外心到三个顶点的距离相等,故本选项说法错误,不符合题意;
D、不在同一条直线上的三个点确定一个圆,故本选项说法正确,符合题意.
故选:D.
【点睛】本题考查圆的认识,垂径定理,三角形的内心与外心,确定圆的条件.熟练掌握这些数学概念的解题的关键.
3.用反证法证明“若的周长为16,则较长边的长不小于4”时,应假设( )
A. B. C. D.
【答案】C
【分析】本题主要考查的是反证法.在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定.反证法的步骤中,第一步是假设结论不成立,反面成立.
【详解】解:用反证法证明:“若的周长为16,则较长边的长不小于4”,
则应先假设,
故选:C.
4.如图,将三块完全相同的等腰直角三角板的一个锐角顶点都放在点处,再使其各有一条直角边恰好在的边上,此时点是( )
A.的外心 B.的内心
C.的重心 D.的垂心
【答案】B
【分析】本题考查三角形内接圆,三角形内心的性质:三角形的内心到三角形三边的距离相等,由点M到的距离相等,从而确定点M是的内心.
【详解】解:根据题意可得:点M到的距离相等,都为等腰直角三角形的腰长,
点M是的内心.
故选:B.
5.如图是一个弓形暗礁区,灯塔A,灯塔B,点C分别在圆周上,现在船只正在安全区航行,若此时,则的大小可能为( )
A. B. C. D.
【答案】A
【分析】本题考查了圆周角定理,三角形外角的性质,设与圆相交于D,连接,根据圆周角定理得出,根据三角形外角的性质得出,即可求解.
【详解】解:如图,设与圆相交于D,连接,
∴,
∵,
∴,
∴选项A符合题意,
故选:A.
6.云南十八怪,草帽当锅盖.使用草编的锅盖蒸米饭,不传热、不吸水、透气性好,搭配攀枝花木甑子,蒸出的米饭香气浓郁,满是家的味道.某同学发现家里的草帽锅盖可以近似看作一个圆锥,测量得母线长为,高度为,通过计算,这个圆锥的侧面展开图的弧长等于( )
A. B. C. D.
【答案】D
【分析】此题考查了圆锥的底面圆锥的周长等于展开的扇形的弧长,勾股定理,
首先根据勾股定理求出底面圆的半径,然后求出底面圆的周长,进而可得到圆锥的侧面展开图的弧长.
【详解】∵母线长为,高度为,
∴底面圆的半径为,
∴底面圆的周长为,
∴这个圆锥的侧面展开图的弧长等于.
故选:D.
7.我们古代数学家擅长通过计算来研究图形的性质.例如《测圆海镜》卷中记载:“假令有圆城一所,不知周径.或问甲、乙二人同立于巽地,乙西行四十八步而立,甲北行九十步,望乙与城参相直,问径几何?”意思是:如图,是直角三角形,,已知步,步,与相切于点分别与相切于为点,求的半径.根据题意,的半径是( )
A.100步 B.120步 C.140步 D.160步
【答案】B
【分析】此题考查了切线的性质,正方形的性质和判定,勾股定理等知识,解题的关键是学会利用参数构建方程解决问题.
如图所示,连接,,,证明四边形是正方形,设步,根据切线长定理,得到步,步,利用勾股定理求出,然后构建方程求解即可.
【详解】如图所示,连接,,,
∵,是的切线
∴,
∴
∵
∴四边形是矩形
∵
∴四边形是正方形
设步,则步,步,
∵,,是的切线
∴步,步,
∵步,
∴
∴
∴.
故选:B.
8.一块含角的直角三角板和一块量角器如图摆放(三角板顶点A与量角器0刻度处重合),量角器与三角板交于点D,经测量知,点E为中点,点F为弧上一动点,则的最小值为( )
A.9 B. C. D.
【答案】C
【分析】本题考查点到圆上的最值问题,等腰三角形的判定与性质,勾股定理及垂径定理,设量角器刻度处为点G,为半圆的直径,设的中点为O,则点O为圆心,连接,证明为等腰直角三角形,由当点O,E,F在一条直线上时,取得最小值,即可解答.
【详解】解:设量角器刻度处为点G,如图,
则为半圆的直径,设的中点为O,则点O为圆心,连接,
∵点E为中点,
∴,,
∵,
∴为等腰直角三角形,
∴,
∴,
∵点F为弧上一动点,
∴当点O,E,F在一条直线上时,取得最小值.
∴的最小值为.
故选:C.
9.如图,在平面直角坐标系中,直线与x轴交于点,与y轴交于点B,,点M在以点为圆心,3为半径的圆上,点N在直线上,若是的切线,则的最小值为( )
A. B. C. D.
【答案】C
【分析】本题主要考查切线的性质,坐标与图形,勾股定理等知识,连接由点A的坐标可求出由得,由是的切线知,由勾股定理得,因为所以当最小时最小,即时最小,运用等积法求出,代入可得结论.
【详解】解:连接如图,
∵,
∴,
∵,
∴;
∴;
∵是的切线,
∴,
∴
∵,
∴当最小时最小,即时最小,
∵
,
又
∴,
∴,
故选:C
10.如图,在中,直径,点D为上方圆上的一点,,于点E,点P是上一点,连接,得出下列结论:
Ⅰ:阴影部分的面积随着点P的位置的改变而改变,其最小值为.
Ⅱ:阴影部分的周长随着点P的位置的改变而改变,其最小值为.
下列判断正确的是( ).
A.只有Ⅰ正确 B.只有Ⅱ正确 C.Ⅰ、Ⅱ都正确 D.Ⅰ、Ⅱ都不正确
【答案】B
【分析】此题考查了扇形面积和弧长、垂径定理、圆周角定理等知识,连接,证明,得到阴影部分的面积为,即可判断Ⅰ;证明当三点共线时,取得最小值,最小值为的长度,即为8,得到阴影部分的周长的最小值为,即可判断Ⅱ.
【详解】解:连接,
∵,
∴,
∵,
∴是等边三角形,
∴,
∵,
∴是等腰三角形,
∵于点E,
∴,
∴,
∴,
∴,
∴阴影部分的面积为
∴阴影部分的面积随着点P的位置的改变而不改变,其值为.
故Ⅰ错误;
∵垂直平分,
∴点D与点B关于对称,
∴,
当三点共线时,取得最小值,最小值为的长度,即为8,
∴阴影部分的周长的最小值为,
∴阴影部分的周长随着点P的位置的改变而改变,其最小值为.
故Ⅱ正确;
故选:B
第II卷(非选择题)
二、填空题(每小题3分,共15分)
11.同一圆中,一条弧所对的圆心角和圆周角分别为和,则 .
【答案】55
【分析】此题考查了圆周角定理.注意掌握掌握一条弧所对的圆心角是圆周角的倍是解题的关键.
【详解】解:由圆周角定理知,,
解得.
故答案为:.
12.如图, 的半径为, 切于点 , 则点到的最小距离是 .
【答案】/
【分析】本题考查了切线的性质,勾股定理,根据勾股定理求得的长,进而根据点到圆的最小距离为,即可求解.
【详解】解:∵切于点 ,
∴,
在中,
∴
∴点到的最小距离是,
故答案为:.
13.如图,正方形内切圆半径为2,点G为边上一点,作正方形,则
【答案】8
【分析】本题考查了正方形的性质,内切圆的性质,根据正方形内切圆半径为2,得出,结合,再代入数值进行计算,即可作答.
【详解】解:依题意,
∵正方形内切圆半径为2
∴
∵四边形是正方形
∴
则
故答案为:8
14.如图,A是外一点,连接交于点B,D是的中点,C是上一点且满足,分别连接,若,则 .
【答案】/度
【分析】此题考查了圆周角定理、等边对等角、三角形内角和定理等知识,先证明,再求出,根据圆周角定理即可得到答案.
【详解】解:连接,
∵D是的中点,
∴,
∵
∴
∴
∴,
∴,
∴
故答案为:
15.工人为了测量某段圆木的直径,把圆木截面、含60°角的三角板和直尺按如图摆放,测得cm,由此可算得该圆木的直径为 cm.
【答案】
【分析】如图,切三角板的斜边于点,连接、,利用邻补角计算出,再根据切线长定理和切线的性质得到平分,,所以,,然后利用含30度角的直角三角形三边的关系得到的长,从而得到圆的直径.
【详解】解:如图,切三角板的斜边于点,连接、,则,
与三角板和直尺相切,
平分,,
,,
在中,
,
cm,
该圆木的直径为cm.
故答案为:.
【点睛】本题考查了切线的性质及切线长定理,熟练掌握切线的性质及切线长定理是解题的关键.
三、解答题(共8小题。共75分。)
16.(8分)在 中,①是直径;②,垂足为;③;④;⑤.
请从上述五个命题中选出两个作为已知条件,三个作为结论并证明.
(1)已知: ,求证: .
(2)证明:
【答案】(1)①②;③④⑤
(2)证明过程见详解
【分析】(1)已知,① 是直径 ;② ,垂足为,求证③ ;④;⑤ ,是证明垂径定理的性质;
(2)如图所示(见详解),连接,可得等腰直角三角形,,由三角形全等即可求证.
【详解】(1)解:根据是直径 ,,垂足为,可证明;;成立,是垂径定理的性质,
∴已知是直径 ,,垂足为,求证;;.
(2)解:如图所示,
是直径 ,,垂足为,连接,,
∵,是半径,,
∴,,,
∴,
∴;
∵,
∴,则,
∴,,同圆中,等角所对的弧相等.
【点睛】本题主要考查圆的垂径定理的性质的证明,掌握圆中直径、半径、弦的位置关系,圆心角与所对弧的关系是解题的关键.
17.(8分)如图,,为⊙O直径,弦,分别交半径,于点G,H,且 .
(1)求证: .
(2)若,且,求的度数.
【答案】(1)见解析
(2)108°
【分析】(1)连接,,根据圆周角定理得出,根据直角三角形的性质得到,根据弧、圆周角关系得出,进而得到,则,根据弧、弦的关系即可得解;
(2)根据等腰三角形的性质、三角形内角和定理、圆周角定理推出,根据弧、圆周角的关系得出,即,求出,根据三角形内角和定理、对顶角性质求解即可.
【详解】(1)证明:如图,连接,
∵为⊙O直径,
∴,
∴,
∵,
∴,
∴,
∵∠FBA=∠EDC,
∴,
∴,
即,
∴,
即,
∴;
(2))解:如图,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵为⊙O直径,
∴度数之和为:,
∴,
∴,
∴,
∴,
∴,
∴ ,
∴的度数为108°.
【点睛】本题考查圆周角定理,等弧,等弦,等角.熟练掌握圆周角定理,以及等弧,等弦,等角是解题的关键.同时考查了等腰三角形的性质,三角形的内角和定理以及外角的性质.
18.(10分)利用素材解决:《桥梁的设计》
某地欲修建一座拱桥,桥的底部两端间的水面宽,称跨度,桥面最高点到的距离称拱高,拱桥的轮廓可以设计成是圆弧型或抛物线型,若修建拱桥的跨度米,拱高米.
方案一 方案二
圆弧型 抛物线型
设计成圆弧型,求该圆弧所在圆的半径. 设计成抛物线型,以AB所在直线为x轴,AB的垂直平分线为y轴建立坐标系,求桥拱的函数表达式.
如图,一艘货船露出水面部分的横截面为矩形,测得米,米.请你通过计算说明货船能否分别顺利通过这两座桥梁.
【答案】任务一:方案一,米;方案二,
任务二:方案一,能通过;方案二,不能通过
【分析】本题考查了二次函数的实际应用,垂径定理,勾股定理的应用,掌握建模的数学思想是解题关键.任务一:方案一,设圆的半径为米,根据即可求解;方案二,设桥拱的函数解析式为,将代入即可求解;任务二:方案一,根据即可判断;方案二,当H点的横坐标时,计算其纵坐标即可判断.
【详解】解:任务一
方案一,设圆的半径为米,
在中,,
(米)
方案二,∵顶点C坐标为,
设桥拱的函数解析式为
代入得,.
函数解析式为.
任务二
方案一,如图,由上得,
在中,
.
能通过
方案二,如图建立直角坐标系,
当H点的横坐标时,,
不能通过.
19.(8分)在等腰中,,过A,B两点的⊙O交射线于点D.
(1)如图1,已知,若点O在上,过点D作⊙O的切线交射线于点E,求的度数.
(2)如图2,已知.与交于点F,过点D作,交射线于点E.求证:是⊙O的切线.
【答案】(1)45°;(2)证明见解析
【分析】(1)利用半径相等以及等边对等角求得,利用切线的性质求得,再根据三角形内角和定理即可求解;
(2)利用圆周角定理求得,利用平行线的性质求得,即可证明是⊙O的切线.
【详解】(1)连接,,
∵,,
∴∠ABC=∠ACB=,∠ABO=∠BAO=,
∴,
∵是切线,
∴,
∴,
在中,;
(2)连接,
∴.
∵,
∴,
∴,
∴是的切线.
【点睛】本题考查了切线的判定和性质,三角形内角和定理,等腰三角形的性质,正确的识别图形是解题的关键.
20.(9分)阅读与思考
如图是小宇同学的数学日记,请仔细阅读,并完成相应的任务.
×年×月×日星期日作三角形的高线已知:如图1,.求作:的高线.今天,我们组的小明和小红的作法和我不同.小明:如图2,①作线段的垂直平分线找到线段的中点O;②以点O为圆心,的长为半径作圆;③延长交于点D;③连接.则线段就是的高线。小红:如图3,①以点B为圆心,的长为半径作弧;②以点C为圆心,的长为半径作弧,两弧交于点E;③作射线,延长与相交于点D.则线段就是的高线.我有如下思考:以上两种办法依据的数学原理是什么呢?
任务:
(1)填空:小明的作法依据的一个数学定理是______;
(2)根据小红的操作过程,求证:是的高线;
(3)在图2中,若延长线段交于点E,,,,请你直接写出的长.
【答案】(1)直径所对的圆周角是直角;
(2)见解析
(3)
【分析】(1)根据作图,结合直径所对的圆周角是直角即可作答;
(2)根据作图,证明是线段的垂直平分线即可作答;
(3)连接、,先求出,,即有,即可得半径,根据弧长公式,问题得解.
【详解】(1)解:根据作图可知:线段是的直径,
即,即有,
则是的高线,
故作法依据的一个数学定理是直径所对的圆周角是直角;
(2)连接,,如图
由作图过程可知:,,
∴点B,点C都在的垂直平分线上,
∴是的垂直平分线,即,
∴是的高线;
(3)连接、,如图,
∵,,
∴,,
∵,,
∴,
∴,
∴半径,
∴.
【点睛】本题考查了圆周角定理,求解弧长以及垂直平分线的判定与性质等知识,掌握圆周角定理是解答本题的关键.
21.(8分)已知四边形内接于,.
(1)如图1,连接,若的半径为6,,求的长;
(2)如图2,连接,若,,对角线平分,求的长.
【答案】(1)
(2)AC
【分析】(1)由90度的圆周角所对的弦是直径得到是直径,则,再利用勾股定理求解即可;
(2)如图2,连接,作于H,先利用勾股定理得到,再由角平分线的定义得到,则可证明,求出,由勾股定理可得. 再证明是等腰直角三角形,同理可得.在中,,据此可得答案.
【详解】(1)解:,
是直径,
∵的半径为6,
.
在中,由勾股定理,得,
∵
∴,
;
(2)解:如图2,连接,作于H,
,,,
.
平分,
,
,
.
四边形内接于,,
,
在中,由根据勾股定理,得,
∴,
∴.
,
∴是等腰直角三角形,
同理可得.
在中,,
.
【点睛】本题主要考查了弧与圆周角之间的关系,90度的圆周角所对的弦是直径,勾股定理,等腰直角三角形的性质与判定,圆内接四边形的性质等等,熟知90度的圆周角所对的弦是直径是解题的关键.
22.(12分)如图,是等边的外接圆,P点是劣弧上的一个动点(不与点A,B 重合).
(1)求的度数;
(2)若,,求的长;
(3)若,点P在劣弧上运动的过程中,
①的值是否为定值,若是,请求出这个定值;若不是,求出其值的取值范围.
②试探究的值是否为定值,若是,请求出这个定值;若不 是,求出其的取值范围.
【答案】(1)
(2)7
(3)①;②的值是定值96.
【分析】(1)首先由等边三角形的性质得到,然后根据圆内接四边形的性质求解即可;
(2)延长到点F使,首先证明出是等边三角形,求出,然后证明出,即可得到;
(3)①首先由(2)可得,,然后得到当点P和点A或点B重合时,的最小值为;当点P,O,C三点共线时,有最大值,然后画出图形,根据勾股定理求解即可;
②延长到点F使,过点A作,由(2)得,是等边三角形,得到,然后根据勾股定理求出,进一步得到,然后结合,代入得到,即可求解.
【详解】(1)解:∵是等边三角形
∴
∵四边形内接于
∴;
(2)如图所示,延长到点F使,
∵
∴
∵
∴是等边三角形
∴,,
∴
∵
∴
∵
∴
∴在和中
∴
∴;
(3)①由(2)可得,
∵点P在劣弧上运动
∴当点P和点A或点B重合时,的长度最小,即或的长度
∵是等边三角形
∴
∴的最小值为
∴的最小值为;
当点P,O,C三点共线时,的长度最大,如图所示,
∴此时是的直径
∴
∵
∴
∴
∴
∵
∴
∴,负值舍去
∴的最大值为8
∴的最大值为8;
∴的值的取值范围是;
②如图所示,延长到点F使,过点A作
由(2)得,是等边三角形
∴
∴,
∴
∵
∴
∴
又∵
∴
.
∴的值是定值96.
【点睛】此题考查了圆与三角形综合题,考查了圆周角定理,等边三角形的性质,圆内接四边形的性质,勾股定理和全等三角形等知识,解题的关键是正确作出辅助线构造等边三角形.
23.(12分)综合与实践
问题情境:小华发现这么一类四边形,有一组对角之和为直角的四边形,小华将这类四边形命名为对余四边形.
猜想证明:
(1)若四边形是对余四边形,则与的度数之和为__________.
(2)如图1,在上有A,B,C三点,是的直径,,相交于点D.四边形是对余四边形吗?若是,请给出证明;若不是,请说明理由,拓展探究:
(3)如图2,在对余四边形中,,,,则线段和之间有怎样的数量关系?请给出你的猜想,并说明理由.
【答案】(1)或;
(2)是,证明见详解;
(3),理由见详解.
【分析】(1)对余四边形的定义即可得出结果;
(2)根据对余四边形的定义,由圆周角定理得出,说明即可;
(3)将绕着点B逆时针旋转得到,连接,利用已知条件得出,利用勾股定理可得结论.
【详解】(1)解:∵四边形是对余四边形,
或
时,.
∴或.
故答案为或.
(2)
证明:是的直径,点A,B,C在上,
.
即.
∴四边形是对余四边形.
(3)猜想:线段和之间的数量关系为:.理由如下:
,
∴将绕着点B逆时针旋转得到,连接,如图,
则,.
.
为等边三角形.
.
,
.
∴∠BFA+∠ADB=30°.
,
.
.
.
.
.
【点睛】本题是圆的综合题,主要考查了对余四边形的定义、圆周角定理、旋转的性质、等边三角形的判定与性质、三角形内角和定理、勾股定理等知识;熟练掌握对余四边形的定义和旋转的性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
