第11-13章阶段检测卷(含解析)2024-2025学年人教版数学八年级上册
文档属性
| 名称 | 第11-13章阶段检测卷(含解析)2024-2025学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 506.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-02 13:55:51 | ||
图片预览


文档简介
第11-13章阶段检测卷-2024-2025学年数学八年级上册人教版
一.选择题(共8小题)
1.(2024秋 西湖区校级月考)下列图形中,是轴对称图形的是( )
A. B.
C. D.
2.(2024秋 船营区校级月考)如图,BE是△ABC的高,正确的是( )
A.
B.
C.
D.
3.(2024秋 乐陵市校级月考)下列说法错误的是( )
A.三角形的三条角平分线都在三角形内部
B.三角形的三条中线都在三角形内部
C.三角形的三条高都在三角形内部
D.三角形的中线、角平分线、高都是线段
4.(2024秋 船营区校级月考)正八边形一个内角的度数是( )
A.150° B.135° C.108° D.60°
5.(2024秋 宜兴市校级月考)根据下列条件,能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D
B.∠A=∠D,∠B=∠E,AC=EF
C.∠A=∠D,∠B=∠E,∠C=∠F
D.AB=DE,BC=EF,∠A=∠D=90°
6.(2024秋 桃城区校级月考)如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
7.(2023秋 行唐县期末)如图,在△ABC中,∠A=90°,∠C=60°,BC=4,则AC的长为( )
A.1 B.1.5 C.2 D.2.5
8.(2023秋 苍梧县期末)如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
A.6个 B.7个 C.8个 D.9个
二.填空题(共8小题)
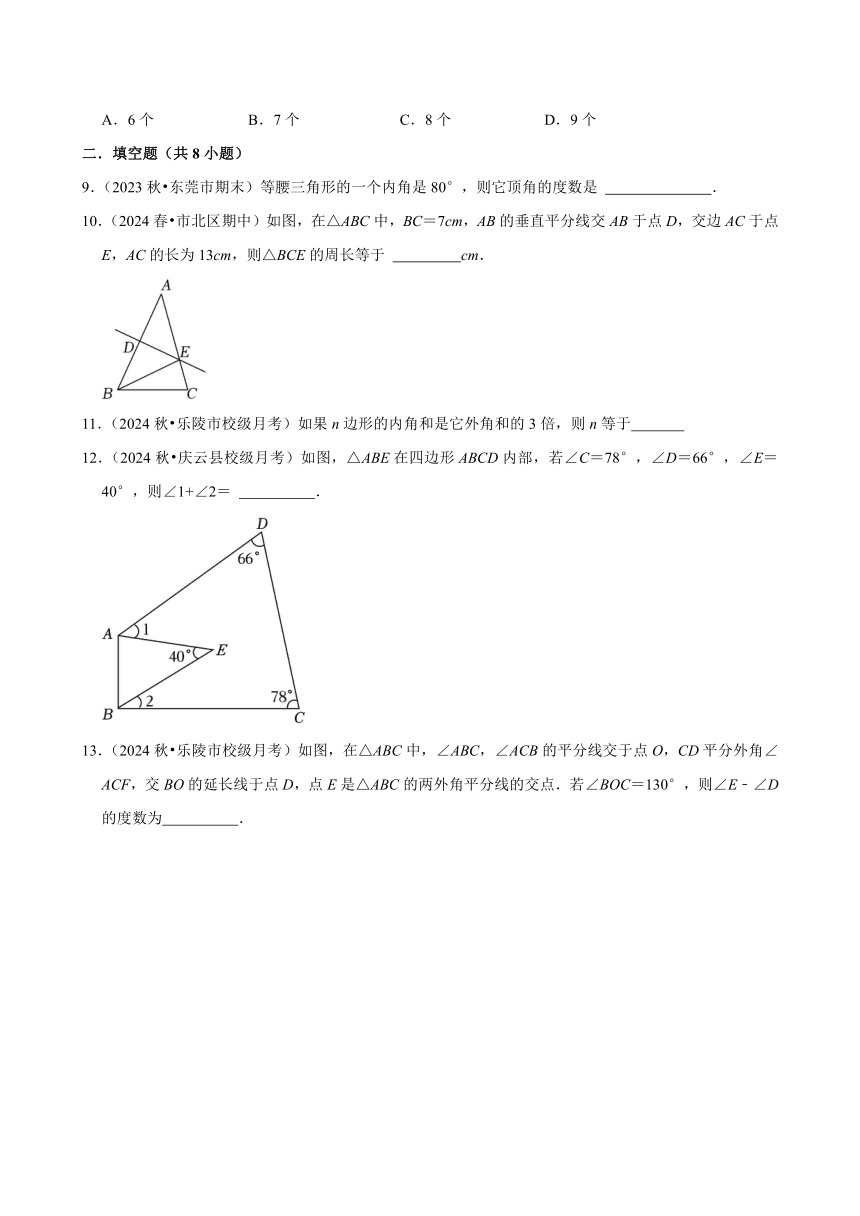
9.(2023秋 东莞市期末)等腰三角形的一个内角是80°,则它顶角的度数是 .
10.(2024春 市北区期中)如图,在△ABC中,BC=7cm,AB的垂直平分线交AB于点D,交边AC于点E,AC的长为13cm,则△BCE的周长等于 cm.
11.(2024秋 乐陵市校级月考)如果n边形的内角和是它外角和的3倍,则n等于
12.(2024秋 庆云县校级月考)如图,△ABE在四边形ABCD内部,若∠C=78°,∠D=66°,∠E=40°,则∠1+∠2= .
13.(2024秋 乐陵市校级月考)如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,CD平分外角∠ACF,交BO的延长线于点D,点E是△ABC的两外角平分线的交点.若∠BOC=130°,则∠E﹣∠D的度数为 .
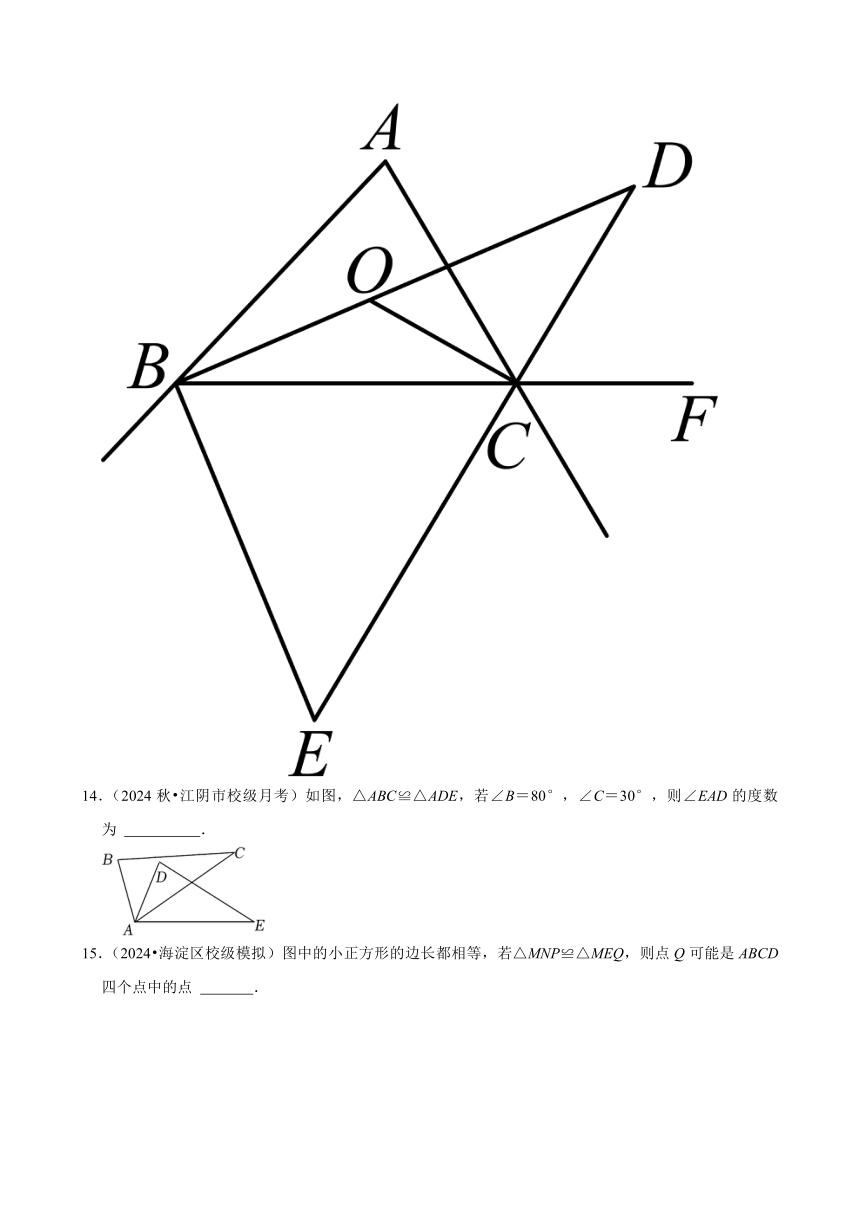
14.(2024秋 江阴市校级月考)如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为 .
15.(2024 海淀区校级模拟)图中的小正方形的边长都相等,若△MNP≌△MEQ,则点Q可能是ABCD四个点中的点 .
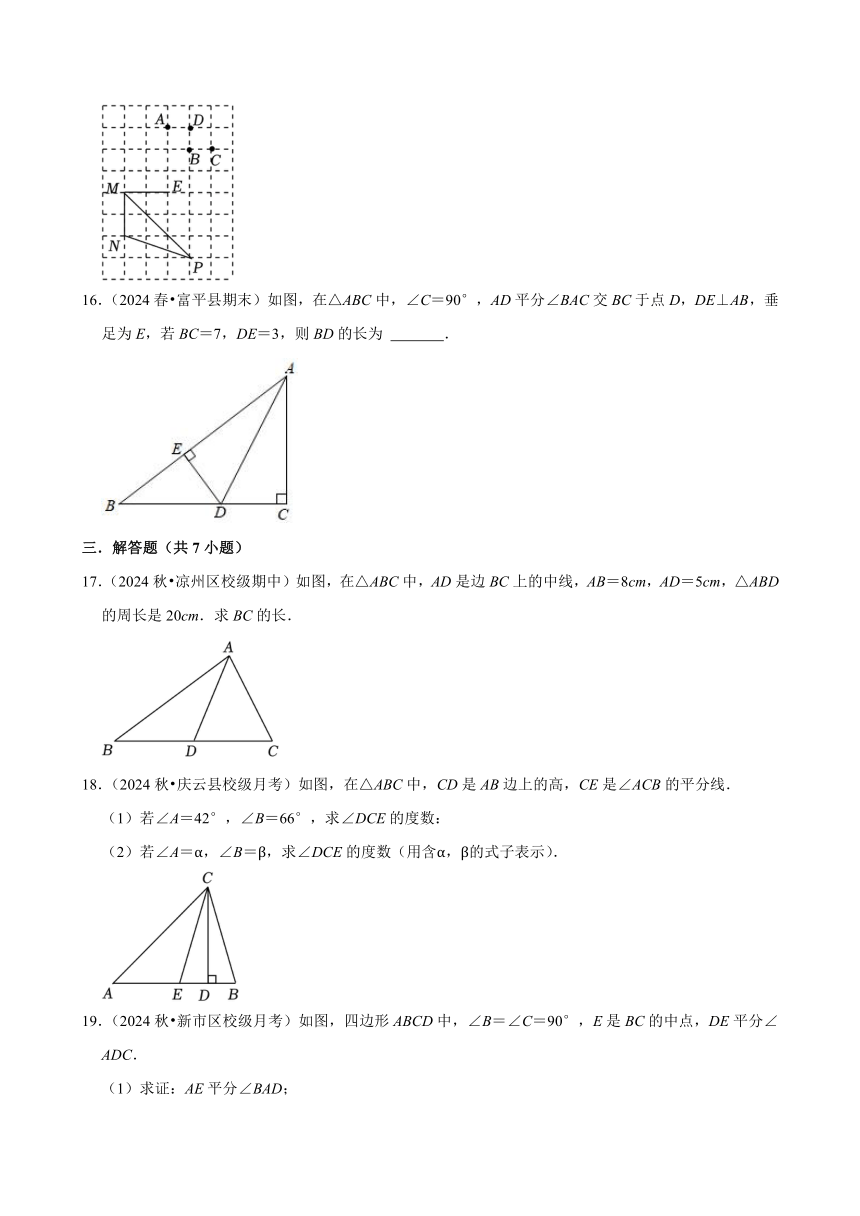
16.(2024春 富平县期末)如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=7,DE=3,则BD的长为 .
三.解答题(共7小题)
17.(2024秋 凉州区校级期中)如图,在△ABC中,AD是边BC上的中线,AB=8cm,AD=5cm,△ABD的周长是20cm.求BC的长.
18.(2024秋 庆云县校级月考)如图,在△ABC中,CD是AB边上的高,CE是∠ACB的平分线.
(1)若∠A=42°,∠B=66°,求∠DCE的度数:
(2)若∠A=α,∠B=β,求∠DCE的度数(用含α,β的式子表示).
19.(2024秋 新市区校级月考)如图,四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.
(1)求证:AE平分∠BAD;
(2)判断AB、CD、AD之间的数量关系,并证明.
20.(2024秋 庆云县校级月考)阅读并完成下面的推理过程以及括号内的理由:
已知:AE=DE,EB=EC,AB=CD,∠ACB=30°.求:∠DBC的度数.
解:因为AE=DE,EC=EB(已知),
所以AE+EC= + (等式的性质).
即CA=BD.
在△ABC和△DCB中,
,
所以△ ≌△ ( ),
所以∠DBC=∠ACB=30°( ).
21.(2024秋 盐都区月考)小明与爸爸妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面0.8m高的B处接住他后用力一推,爸爸在C处接住他,若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和2m,∠BOC=90°.
(1)△OBD与△COE全等吗?请说明理由;
(2)小明的爸爸是在距离地面多高的地方接住小明的?
22.(2024春 城关区期末)如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E.
(1)∠DAE=40°,求∠BAC的度数;
(2)若△ADE的周长为18,求BC的长度.
23.(2024秋 江阴市校级月考)某数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别在射线AB、AC上.
活动一:如图1所示,从点A1开始,依次向右摆放小棒,使小棒在端点处互相垂直,A1A2为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?答: .(填“能”或“不能”)
(2)设AA1=A1A2=A2A3,θ= °.
活动二:如图2所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.
数学思考:
(3)若已经摆放了3根小棒,则θ3= ;(用含θ的式子表示)
(4)若只能摆放4根小棒,则θ的范围是 .
第11-13章阶段检测卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共8小题)
1.(2024秋 西湖区校级月考)下列图形中,是轴对称图形的是( )
A. B.
C. D.
【解答】解:选项A、B、D的图形均不能找到这样的一条直线,使图形沿该直线对折后直线两旁的部分能够完全重合,所以不是轴对称图形,
选项C的图形能找到这样的一条直线,使图形沿该直线对折后直线两旁的部分能够完全重合,所以是轴对称图形.
故选:C.
2.(2024秋 船营区校级月考)如图,BE是△ABC的高,正确的是( )
A.
B.
C.
D.
【解答】解:由题意:BE是△ABC的高,可得:
故选:C.
3.(2024秋 乐陵市校级月考)下列说法错误的是( )
A.三角形的三条角平分线都在三角形内部
B.三角形的三条中线都在三角形内部
C.三角形的三条高都在三角形内部
D.三角形的中线、角平分线、高都是线段
【解答】A.三角形的三条角平分线都在三角形内部,正确,不符合题意;
B.三角形的三条中线都在三角形内部,正确,不符合题意;
C.三角形的三条高可在三角形内部,也可在外部,原说法错误,符合题意;
D.三角形的中线、角平分线、高都是线段,正确,不符合题意;
故选:C.
4.(2024秋 船营区校级月考)正八边形一个内角的度数是( )
A.150° B.135° C.108° D.60°
【解答】解:∵正多边形的每一个内角相等,则对应的外角也相等,
∴正八边形的一个外角等于360÷8=45°,
∴正八边形的一个内角为180°﹣45°=135°.
故选:B.
5.(2024秋 宜兴市校级月考)根据下列条件,能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D
B.∠A=∠D,∠B=∠E,AC=EF
C.∠A=∠D,∠B=∠E,∠C=∠F
D.AB=DE,BC=EF,∠A=∠D=90°
【解答】解:A、∠A、∠D分别是BC和EF的对边,条件不能判定△ABC≌△DEF,故A不符合题意;
B、∠B的对边是AC,∠E的对边是DF,条件不能判定△ABC≌△DEF,故B不符合题意;
C、缺少边相等的条件,三个角对应相等不能判定△ABC≌△DEF,故C不符合题意;
D、AB=DE,BC=EF,∠A=∠D=90°,由HL能判定△ABC≌△DEF,故D符合题意.
故选:D.
6.(2024秋 桃城区校级月考)如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
【解答】解:∵△ABC≌△AEF,
∴AC=AF,故①正确;
∠EAF=∠BAC,
∴∠FAC=∠EAB≠∠FAB,故②错误;
EF=BC,故③正确;
∠EAB=∠FAC,故④正确;
综上所述,结论正确的是①③④共3个.
故选:C.
7.(2023秋 行唐县期末)如图,在△ABC中,∠A=90°,∠C=60°,BC=4,则AC的长为( )
A.1 B.1.5 C.2 D.2.5
【解答】解:由题意知,∠B=180°﹣∠A﹣∠C=30°,
∴,
故选:C.
8.(2023秋 苍梧县期末)如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
A.6个 B.7个 C.8个 D.9个
【解答】解:如图,分情况讨论:
①AB为等腰△ABC的底边时,符合条件的C点有4个;
②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.
故选:C.
二.填空题(共8小题)
9.(2023秋 东莞市期末)等腰三角形的一个内角是80°,则它顶角的度数是 80°或20° .
【解答】解:当80°是等腰三角形的顶角时,则顶角就是80°;
当80°是等腰三角形的底角时,则顶角是180°﹣80°×2=20°.
故答案为:80°或20°.
10.(2024春 市北区期中)如图,在△ABC中,BC=7cm,AB的垂直平分线交AB于点D,交边AC于点E,AC的长为13cm,则△BCE的周长等于 20 cm.
【解答】解:∵DE是AB的垂直平分线,
∴AE=BE,
∵BC=7cm,AC的长为13cm,
∴△BCE的周长=BC+CE+BE=BC+CE+AE=BC+AC=20cm.
故答案为:20.
11.(2024秋 乐陵市校级月考)如果n边形的内角和是它外角和的3倍,则n等于 8
【解答】解:根据多边形内角和公式180°(n﹣2)和外角和为360°可得:
180(n﹣2)=360×3,
∴n=8,
故答案为:8.
12.(2024秋 庆云县校级月考)如图,△ABE在四边形ABCD内部,若∠C=78°,∠D=66°,∠E=40°,则∠1+∠2= 76° .
【解答】解:在△ABE中,∠E=40°,
∴∠EAB+∠EBA=180°﹣∠E=140°,
∴∠DAB+∠CBA=∠1+∠2+(∠EAB+∠EBA)=∠1+∠2+140°
在四边形ABCD中,∠DAB+∠CBA+∠C+∠D=360°,
∵∠C=78°,∠D=66°,
∴∠1+∠2+140°+78°+66°=360°,
∴∠1+∠2=76°,
故答案为:76°.
13.(2024秋 乐陵市校级月考)如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,CD平分外角∠ACF,交BO的延长线于点D,点E是△ABC的两外角平分线的交点.若∠BOC=130°,则∠E﹣∠D的度数为 10° .
【解答】解:∵OB平分∠ABC,OC平分∠ACB,CD平分∠ACF,CE平分∠ABC,BE平分∠FBG,
∴
=,
解得:∠A=80°,
∴
=,
∴
=,
∴∠E﹣∠D=50°﹣40°=10°,
故答案为:10°.
14.(2024秋 江阴市校级月考)如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为 70° .
【解答】解:∵△ABC≌△ADE,∠B=80°,∠C=30°,
∴∠B=∠D=80°,∠E=∠C=30°,
∴∠EAD=180°﹣∠D﹣∠E=70°,
故答案为:70°.
15.(2024 海淀区校级模拟)图中的小正方形的边长都相等,若△MNP≌△MEQ,则点Q可能是ABCD四个点中的点 D .
【解答】解:∵△MNP≌△MEQ,
∴点Q应是图中的D点,如图,
故答案为:D.
16.(2024春 富平县期末)如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=7,DE=3,则BD的长为 4 .
【解答】解:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴CD=DE,
∵DE=3,
∴CD=3,
∴BD=BC﹣CD=7﹣3=4.
故答案为:4.
三.解答题(共7小题)
17.(2024秋 凉州区校级期中)如图,在△ABC中,AD是边BC上的中线,AB=8cm,AD=5cm,△ABD的周长是20cm.求BC的长.
【解答】解:∵AD是边BC上的中线,
∴BD=20﹣AB﹣AD=20﹣8﹣5=7(cm),
∵AD是边BC上的中线,
∴BC=2BD=2×7=14(cm).
18.(2024秋 庆云县校级月考)如图,在△ABC中,CD是AB边上的高,CE是∠ACB的平分线.
(1)若∠A=42°,∠B=66°,求∠DCE的度数:
(2)若∠A=α,∠B=β,求∠DCE的度数(用含α,β的式子表示).
【解答】解:(1)∵∠A=42°,∠B=66°,
∴∠A C B=180°﹣∠A﹣∠B=72°,
∵CE是∠ACB的平分线,
∴,
∵CD是AB边上的高,
∴∠BDC=90°,
∴∠BCD=90°﹣∠B=90°﹣66°=24°,
∴∠DCE=∠ECB﹣∠BCD=36°﹣24°=12°;
(2)∵∠A=α,∠B=β,
∴∠ACB=180°﹣∠A﹣∠B=180°﹣α﹣β,
∵CE是∠ACB的平分线,
∴,
∵CD是AB边上的高,
∴∠BDC=90°,
∴∠BCD=90°﹣∠B=90°﹣β,
∴.
19.(2024秋 新市区校级月考)如图,四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.
(1)求证:AE平分∠BAD;
(2)判断AB、CD、AD之间的数量关系,并证明.
【解答】(1)证明:过点E作EF⊥DA于点F,
∵∠C=90°,DE平分∠ADC,
∴CE=EF,
∵E是BC的中点,
∴BE=CE,
∴BE=EF,
又∵∠B=90°,EF⊥DA,
∴AE平分∠BAD.
(2)解:AD=CD+AB,理由如下,
∵∠C=∠DFE=90°,
∴在Rt△DFE和Rt△DCE中,
,
∴Rt△DFE≌Rt△DCE(HL),
∴DC=DF,
同理AF=AB,
∵AD=AF+DF,
∴AD=CD+AB.
20.(2024秋 庆云县校级月考)阅读并完成下面的推理过程以及括号内的理由:
已知:AE=DE,EB=EC,AB=CD,∠ACB=30°.求:∠DBC的度数.
解:因为AE=DE,EC=EB(已知),
所以AE+EC= DE + EB (等式的性质).
即CA=BD.
在△ABC和△DCB中,
,
所以△ ABC ≌△ △DCB ( SSS ),
所以∠DBC=∠ACB=30°( 全等三角形的对应角相等 ).
【解答】解:因为AE=DE,EC=EB(已知),
所以AE+EC=DE+EB(等式的性质),
即CA=BD,
在△ABC和△DCB中,
,
所以△ABC≌△DCB(SSS),
所以∠ACB=∠DBC=30°(全等三角形的对应角相等),
故答案为:DE;EB;ABC;DCB;SSS;全等三角形的对应角相等.
21.(2024秋 盐都区月考)小明与爸爸妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面0.8m高的B处接住他后用力一推,爸爸在C处接住他,若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和2m,∠BOC=90°.
(1)△OBD与△COE全等吗?请说明理由;
(2)小明的爸爸是在距离地面多高的地方接住小明的?
【解答】解:(1)△OBD与△COE全等.理由如下:
由题意可知∠CEO=∠BDO=90°,BO=CO,∠BOC=90°,
∴∠COE+∠BOD=∠BOD+∠OBD=90°,
∴∠COE=∠OBD,
在△COE 和△OBD中,
,
∴△COE≌△OBD(AAS);
(2)∵△COE≌△OBD,
∴CE=OD,OE=BD,
又∵BD、CE分别为1.4m和2m,
∴DE=OD﹣OE=CE﹣BD=2﹣1.4=0.6(m),
∴AE=DE+AD=0.6+0.8=1.4(m).
答:小明的爸爸是在距离地面1.4m处接住小明的.
22.(2024春 城关区期末)如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E.
(1)∠DAE=40°,求∠BAC的度数;
(2)若△ADE的周长为18,求BC的长度.
【解答】解:(1)∵DM垂直平分AB,
∴DA=DB,
∴∠DAB=∠B,
∵∠ADE+∠ADB=180°,∠DAB+∠B+∠ADB=180°,
∴∠ADE=∠DAB+∠B=2∠B,
同理:EA=EC,∠AED=2∠C,
∵∠ADE+∠AED+∠DAE=180°,∠DAE=40°,
∴∠ADE+∠AED=180°﹣∠DAE=140°,
即2∠B+2∠C=140°,
∴∠B+∠C=70°,
∴∠BAC=180°﹣(∠B+∠C)=110°;
(2)∵△ADE的周长为18,
∴DA+DE+AE=18,
由(1)可知:DA=DB,EA=EC,
∴DB+DE+EC=18,
∴BC=18.
23.(2024秋 江阴市校级月考)某数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别在射线AB、AC上.
活动一:如图1所示,从点A1开始,依次向右摆放小棒,使小棒在端点处互相垂直,A1A2为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?答: 能 .(填“能”或“不能”)
(2)设AA1=A1A2=A2A3,θ= 22.5 °.
活动二:如图2所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.
数学思考:
(3)若已经摆放了3根小棒,则θ3= 4θ ;(用含θ的式子表示)
(4)若只能摆放4根小棒,则θ的范围是 18°≤θ<22.5° .
【解答】解:(1)∵根据已知条件∠BAC=θ(0°<θ<90°)小棒两端能分别落在两射线上,
∴小棒能继续摆下去,
故答案为:能;
(2)∵A1A2=A2A3,A1A2⊥A2A3,
∴∠A2A1A3=45°,
∴∠AA2A1+θ=45°,
∵A1A2=AA1,
∴∠AA2A1=∠A=θ,
∴θ=45°÷2=22.5°;
(3)∵A1A2=AA1,
∴∠A1AA2=∠AA2A1=θ,
∴∠A2A1A3=θ1=θ+θ=2θ,
即θ1=2θ,
同理可得:θ2=3θ,θ3=4θ,
故答案为:4θ;
(4)由题意得:,
∴18°≤θ<22.5°,
故答案为:18°≤θ<22.5°.
一.选择题(共8小题)
1.(2024秋 西湖区校级月考)下列图形中,是轴对称图形的是( )
A. B.
C. D.
2.(2024秋 船营区校级月考)如图,BE是△ABC的高,正确的是( )
A.
B.
C.
D.
3.(2024秋 乐陵市校级月考)下列说法错误的是( )
A.三角形的三条角平分线都在三角形内部
B.三角形的三条中线都在三角形内部
C.三角形的三条高都在三角形内部
D.三角形的中线、角平分线、高都是线段
4.(2024秋 船营区校级月考)正八边形一个内角的度数是( )
A.150° B.135° C.108° D.60°
5.(2024秋 宜兴市校级月考)根据下列条件,能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D
B.∠A=∠D,∠B=∠E,AC=EF
C.∠A=∠D,∠B=∠E,∠C=∠F
D.AB=DE,BC=EF,∠A=∠D=90°
6.(2024秋 桃城区校级月考)如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
7.(2023秋 行唐县期末)如图,在△ABC中,∠A=90°,∠C=60°,BC=4,则AC的长为( )
A.1 B.1.5 C.2 D.2.5
8.(2023秋 苍梧县期末)如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
A.6个 B.7个 C.8个 D.9个
二.填空题(共8小题)
9.(2023秋 东莞市期末)等腰三角形的一个内角是80°,则它顶角的度数是 .
10.(2024春 市北区期中)如图,在△ABC中,BC=7cm,AB的垂直平分线交AB于点D,交边AC于点E,AC的长为13cm,则△BCE的周长等于 cm.
11.(2024秋 乐陵市校级月考)如果n边形的内角和是它外角和的3倍,则n等于
12.(2024秋 庆云县校级月考)如图,△ABE在四边形ABCD内部,若∠C=78°,∠D=66°,∠E=40°,则∠1+∠2= .
13.(2024秋 乐陵市校级月考)如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,CD平分外角∠ACF,交BO的延长线于点D,点E是△ABC的两外角平分线的交点.若∠BOC=130°,则∠E﹣∠D的度数为 .
14.(2024秋 江阴市校级月考)如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为 .
15.(2024 海淀区校级模拟)图中的小正方形的边长都相等,若△MNP≌△MEQ,则点Q可能是ABCD四个点中的点 .
16.(2024春 富平县期末)如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=7,DE=3,则BD的长为 .
三.解答题(共7小题)
17.(2024秋 凉州区校级期中)如图,在△ABC中,AD是边BC上的中线,AB=8cm,AD=5cm,△ABD的周长是20cm.求BC的长.
18.(2024秋 庆云县校级月考)如图,在△ABC中,CD是AB边上的高,CE是∠ACB的平分线.
(1)若∠A=42°,∠B=66°,求∠DCE的度数:
(2)若∠A=α,∠B=β,求∠DCE的度数(用含α,β的式子表示).
19.(2024秋 新市区校级月考)如图,四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.
(1)求证:AE平分∠BAD;
(2)判断AB、CD、AD之间的数量关系,并证明.
20.(2024秋 庆云县校级月考)阅读并完成下面的推理过程以及括号内的理由:
已知:AE=DE,EB=EC,AB=CD,∠ACB=30°.求:∠DBC的度数.
解:因为AE=DE,EC=EB(已知),
所以AE+EC= + (等式的性质).
即CA=BD.
在△ABC和△DCB中,
,
所以△ ≌△ ( ),
所以∠DBC=∠ACB=30°( ).
21.(2024秋 盐都区月考)小明与爸爸妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面0.8m高的B处接住他后用力一推,爸爸在C处接住他,若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和2m,∠BOC=90°.
(1)△OBD与△COE全等吗?请说明理由;
(2)小明的爸爸是在距离地面多高的地方接住小明的?
22.(2024春 城关区期末)如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E.
(1)∠DAE=40°,求∠BAC的度数;
(2)若△ADE的周长为18,求BC的长度.
23.(2024秋 江阴市校级月考)某数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别在射线AB、AC上.
活动一:如图1所示,从点A1开始,依次向右摆放小棒,使小棒在端点处互相垂直,A1A2为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?答: .(填“能”或“不能”)
(2)设AA1=A1A2=A2A3,θ= °.
活动二:如图2所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.
数学思考:
(3)若已经摆放了3根小棒,则θ3= ;(用含θ的式子表示)
(4)若只能摆放4根小棒,则θ的范围是 .
第11-13章阶段检测卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共8小题)
1.(2024秋 西湖区校级月考)下列图形中,是轴对称图形的是( )
A. B.
C. D.
【解答】解:选项A、B、D的图形均不能找到这样的一条直线,使图形沿该直线对折后直线两旁的部分能够完全重合,所以不是轴对称图形,
选项C的图形能找到这样的一条直线,使图形沿该直线对折后直线两旁的部分能够完全重合,所以是轴对称图形.
故选:C.
2.(2024秋 船营区校级月考)如图,BE是△ABC的高,正确的是( )
A.
B.
C.
D.
【解答】解:由题意:BE是△ABC的高,可得:
故选:C.
3.(2024秋 乐陵市校级月考)下列说法错误的是( )
A.三角形的三条角平分线都在三角形内部
B.三角形的三条中线都在三角形内部
C.三角形的三条高都在三角形内部
D.三角形的中线、角平分线、高都是线段
【解答】A.三角形的三条角平分线都在三角形内部,正确,不符合题意;
B.三角形的三条中线都在三角形内部,正确,不符合题意;
C.三角形的三条高可在三角形内部,也可在外部,原说法错误,符合题意;
D.三角形的中线、角平分线、高都是线段,正确,不符合题意;
故选:C.
4.(2024秋 船营区校级月考)正八边形一个内角的度数是( )
A.150° B.135° C.108° D.60°
【解答】解:∵正多边形的每一个内角相等,则对应的外角也相等,
∴正八边形的一个外角等于360÷8=45°,
∴正八边形的一个内角为180°﹣45°=135°.
故选:B.
5.(2024秋 宜兴市校级月考)根据下列条件,能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D
B.∠A=∠D,∠B=∠E,AC=EF
C.∠A=∠D,∠B=∠E,∠C=∠F
D.AB=DE,BC=EF,∠A=∠D=90°
【解答】解:A、∠A、∠D分别是BC和EF的对边,条件不能判定△ABC≌△DEF,故A不符合题意;
B、∠B的对边是AC,∠E的对边是DF,条件不能判定△ABC≌△DEF,故B不符合题意;
C、缺少边相等的条件,三个角对应相等不能判定△ABC≌△DEF,故C不符合题意;
D、AB=DE,BC=EF,∠A=∠D=90°,由HL能判定△ABC≌△DEF,故D符合题意.
故选:D.
6.(2024秋 桃城区校级月考)如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
【解答】解:∵△ABC≌△AEF,
∴AC=AF,故①正确;
∠EAF=∠BAC,
∴∠FAC=∠EAB≠∠FAB,故②错误;
EF=BC,故③正确;
∠EAB=∠FAC,故④正确;
综上所述,结论正确的是①③④共3个.
故选:C.
7.(2023秋 行唐县期末)如图,在△ABC中,∠A=90°,∠C=60°,BC=4,则AC的长为( )
A.1 B.1.5 C.2 D.2.5
【解答】解:由题意知,∠B=180°﹣∠A﹣∠C=30°,
∴,
故选:C.
8.(2023秋 苍梧县期末)如图所示的正方形网格中,网格线的交点称为格点.已知A、B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则点C的个数是( )
A.6个 B.7个 C.8个 D.9个
【解答】解:如图,分情况讨论:
①AB为等腰△ABC的底边时,符合条件的C点有4个;
②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.
故选:C.
二.填空题(共8小题)
9.(2023秋 东莞市期末)等腰三角形的一个内角是80°,则它顶角的度数是 80°或20° .
【解答】解:当80°是等腰三角形的顶角时,则顶角就是80°;
当80°是等腰三角形的底角时,则顶角是180°﹣80°×2=20°.
故答案为:80°或20°.
10.(2024春 市北区期中)如图,在△ABC中,BC=7cm,AB的垂直平分线交AB于点D,交边AC于点E,AC的长为13cm,则△BCE的周长等于 20 cm.
【解答】解:∵DE是AB的垂直平分线,
∴AE=BE,
∵BC=7cm,AC的长为13cm,
∴△BCE的周长=BC+CE+BE=BC+CE+AE=BC+AC=20cm.
故答案为:20.
11.(2024秋 乐陵市校级月考)如果n边形的内角和是它外角和的3倍,则n等于 8
【解答】解:根据多边形内角和公式180°(n﹣2)和外角和为360°可得:
180(n﹣2)=360×3,
∴n=8,
故答案为:8.
12.(2024秋 庆云县校级月考)如图,△ABE在四边形ABCD内部,若∠C=78°,∠D=66°,∠E=40°,则∠1+∠2= 76° .
【解答】解:在△ABE中,∠E=40°,
∴∠EAB+∠EBA=180°﹣∠E=140°,
∴∠DAB+∠CBA=∠1+∠2+(∠EAB+∠EBA)=∠1+∠2+140°
在四边形ABCD中,∠DAB+∠CBA+∠C+∠D=360°,
∵∠C=78°,∠D=66°,
∴∠1+∠2+140°+78°+66°=360°,
∴∠1+∠2=76°,
故答案为:76°.
13.(2024秋 乐陵市校级月考)如图,在△ABC中,∠ABC,∠ACB的平分线交于点O,CD平分外角∠ACF,交BO的延长线于点D,点E是△ABC的两外角平分线的交点.若∠BOC=130°,则∠E﹣∠D的度数为 10° .
【解答】解:∵OB平分∠ABC,OC平分∠ACB,CD平分∠ACF,CE平分∠ABC,BE平分∠FBG,
∴
=,
解得:∠A=80°,
∴
=,
∴
=,
∴∠E﹣∠D=50°﹣40°=10°,
故答案为:10°.
14.(2024秋 江阴市校级月考)如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为 70° .
【解答】解:∵△ABC≌△ADE,∠B=80°,∠C=30°,
∴∠B=∠D=80°,∠E=∠C=30°,
∴∠EAD=180°﹣∠D﹣∠E=70°,
故答案为:70°.
15.(2024 海淀区校级模拟)图中的小正方形的边长都相等,若△MNP≌△MEQ,则点Q可能是ABCD四个点中的点 D .
【解答】解:∵△MNP≌△MEQ,
∴点Q应是图中的D点,如图,
故答案为:D.
16.(2024春 富平县期末)如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于点D,DE⊥AB,垂足为E,若BC=7,DE=3,则BD的长为 4 .
【解答】解:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴CD=DE,
∵DE=3,
∴CD=3,
∴BD=BC﹣CD=7﹣3=4.
故答案为:4.
三.解答题(共7小题)
17.(2024秋 凉州区校级期中)如图,在△ABC中,AD是边BC上的中线,AB=8cm,AD=5cm,△ABD的周长是20cm.求BC的长.
【解答】解:∵AD是边BC上的中线,
∴BD=20﹣AB﹣AD=20﹣8﹣5=7(cm),
∵AD是边BC上的中线,
∴BC=2BD=2×7=14(cm).
18.(2024秋 庆云县校级月考)如图,在△ABC中,CD是AB边上的高,CE是∠ACB的平分线.
(1)若∠A=42°,∠B=66°,求∠DCE的度数:
(2)若∠A=α,∠B=β,求∠DCE的度数(用含α,β的式子表示).
【解答】解:(1)∵∠A=42°,∠B=66°,
∴∠A C B=180°﹣∠A﹣∠B=72°,
∵CE是∠ACB的平分线,
∴,
∵CD是AB边上的高,
∴∠BDC=90°,
∴∠BCD=90°﹣∠B=90°﹣66°=24°,
∴∠DCE=∠ECB﹣∠BCD=36°﹣24°=12°;
(2)∵∠A=α,∠B=β,
∴∠ACB=180°﹣∠A﹣∠B=180°﹣α﹣β,
∵CE是∠ACB的平分线,
∴,
∵CD是AB边上的高,
∴∠BDC=90°,
∴∠BCD=90°﹣∠B=90°﹣β,
∴.
19.(2024秋 新市区校级月考)如图,四边形ABCD中,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.
(1)求证:AE平分∠BAD;
(2)判断AB、CD、AD之间的数量关系,并证明.
【解答】(1)证明:过点E作EF⊥DA于点F,
∵∠C=90°,DE平分∠ADC,
∴CE=EF,
∵E是BC的中点,
∴BE=CE,
∴BE=EF,
又∵∠B=90°,EF⊥DA,
∴AE平分∠BAD.
(2)解:AD=CD+AB,理由如下,
∵∠C=∠DFE=90°,
∴在Rt△DFE和Rt△DCE中,
,
∴Rt△DFE≌Rt△DCE(HL),
∴DC=DF,
同理AF=AB,
∵AD=AF+DF,
∴AD=CD+AB.
20.(2024秋 庆云县校级月考)阅读并完成下面的推理过程以及括号内的理由:
已知:AE=DE,EB=EC,AB=CD,∠ACB=30°.求:∠DBC的度数.
解:因为AE=DE,EC=EB(已知),
所以AE+EC= DE + EB (等式的性质).
即CA=BD.
在△ABC和△DCB中,
,
所以△ ABC ≌△ △DCB ( SSS ),
所以∠DBC=∠ACB=30°( 全等三角形的对应角相等 ).
【解答】解:因为AE=DE,EC=EB(已知),
所以AE+EC=DE+EB(等式的性质),
即CA=BD,
在△ABC和△DCB中,
,
所以△ABC≌△DCB(SSS),
所以∠ACB=∠DBC=30°(全等三角形的对应角相等),
故答案为:DE;EB;ABC;DCB;SSS;全等三角形的对应角相等.
21.(2024秋 盐都区月考)小明与爸爸妈妈在公园里荡秋千,如图,小明坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面0.8m高的B处接住他后用力一推,爸爸在C处接住他,若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和2m,∠BOC=90°.
(1)△OBD与△COE全等吗?请说明理由;
(2)小明的爸爸是在距离地面多高的地方接住小明的?
【解答】解:(1)△OBD与△COE全等.理由如下:
由题意可知∠CEO=∠BDO=90°,BO=CO,∠BOC=90°,
∴∠COE+∠BOD=∠BOD+∠OBD=90°,
∴∠COE=∠OBD,
在△COE 和△OBD中,
,
∴△COE≌△OBD(AAS);
(2)∵△COE≌△OBD,
∴CE=OD,OE=BD,
又∵BD、CE分别为1.4m和2m,
∴DE=OD﹣OE=CE﹣BD=2﹣1.4=0.6(m),
∴AE=DE+AD=0.6+0.8=1.4(m).
答:小明的爸爸是在距离地面1.4m处接住小明的.
22.(2024春 城关区期末)如图所示,在△ABC中,DM、EN分别垂直平分AB和AC,交BC于D、E.
(1)∠DAE=40°,求∠BAC的度数;
(2)若△ADE的周长为18,求BC的长度.
【解答】解:(1)∵DM垂直平分AB,
∴DA=DB,
∴∠DAB=∠B,
∵∠ADE+∠ADB=180°,∠DAB+∠B+∠ADB=180°,
∴∠ADE=∠DAB+∠B=2∠B,
同理:EA=EC,∠AED=2∠C,
∵∠ADE+∠AED+∠DAE=180°,∠DAE=40°,
∴∠ADE+∠AED=180°﹣∠DAE=140°,
即2∠B+2∠C=140°,
∴∠B+∠C=70°,
∴∠BAC=180°﹣(∠B+∠C)=110°;
(2)∵△ADE的周长为18,
∴DA+DE+AE=18,
由(1)可知:DA=DB,EA=EC,
∴DB+DE+EC=18,
∴BC=18.
23.(2024秋 江阴市校级月考)某数学兴趣小组开展了一次活动,过程如下:设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别在射线AB、AC上.
活动一:如图1所示,从点A1开始,依次向右摆放小棒,使小棒在端点处互相垂直,A1A2为第1根小棒.
数学思考:
(1)小棒能无限摆下去吗?答: 能 .(填“能”或“不能”)
(2)设AA1=A1A2=A2A3,θ= 22.5 °.
活动二:如图2所示,从点A1开始,用等长的小棒依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.
数学思考:
(3)若已经摆放了3根小棒,则θ3= 4θ ;(用含θ的式子表示)
(4)若只能摆放4根小棒,则θ的范围是 18°≤θ<22.5° .
【解答】解:(1)∵根据已知条件∠BAC=θ(0°<θ<90°)小棒两端能分别落在两射线上,
∴小棒能继续摆下去,
故答案为:能;
(2)∵A1A2=A2A3,A1A2⊥A2A3,
∴∠A2A1A3=45°,
∴∠AA2A1+θ=45°,
∵A1A2=AA1,
∴∠AA2A1=∠A=θ,
∴θ=45°÷2=22.5°;
(3)∵A1A2=AA1,
∴∠A1AA2=∠AA2A1=θ,
∴∠A2A1A3=θ1=θ+θ=2θ,
即θ1=2θ,
同理可得:θ2=3θ,θ3=4θ,
故答案为:4θ;
(4)由题意得:,
∴18°≤θ<22.5°,
故答案为:18°≤θ<22.5°.
