期中复习卷(含解析)2024-2025学年人教版数学八年级上册
文档属性
| 名称 | 期中复习卷(含解析)2024-2025学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 626.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-02 14:06:45 | ||
图片预览



文档简介
期中复习卷-2024-2025学年数学八年级上册人教版
一.选择题(共10小题)
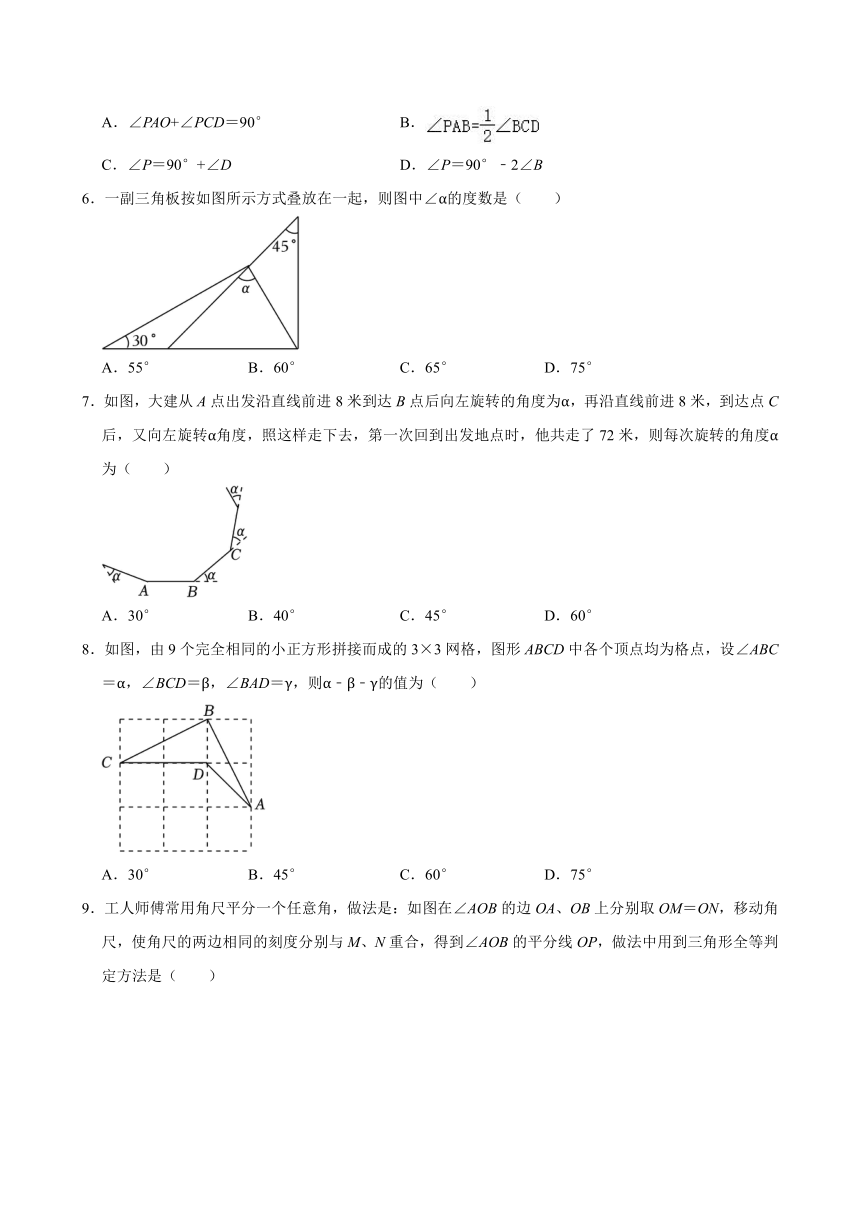
1.下列图形中,不是轴对称图形的是( )
A. B.
C. D.
2.某三角形的三边长分别为3,6,x,则x不可能是( )
A.3.5 B.6 C.7.3 D.9.2
3.已知A(﹣1,3),B(﹣1,﹣3),则下面结论中正确的是( )
A.A,B两点关于y轴对称 B.点A到y轴距离是3
C.点B到x轴距离是1 D.AB∥y轴
4.将一副三角板如图摆放,则图中∠1的度数是( )
A.105° B.120° C.135° D.150°
5.如图,AD交BC于点O,∠BAD的平分线与△OCD的外角∠OCE的平分线交于点P,∠B=∠D,则下列说法不正确的是( )
A.∠PAO+∠PCD=90° B.
C.∠P=90°+∠D D.∠P=90°﹣2∠B
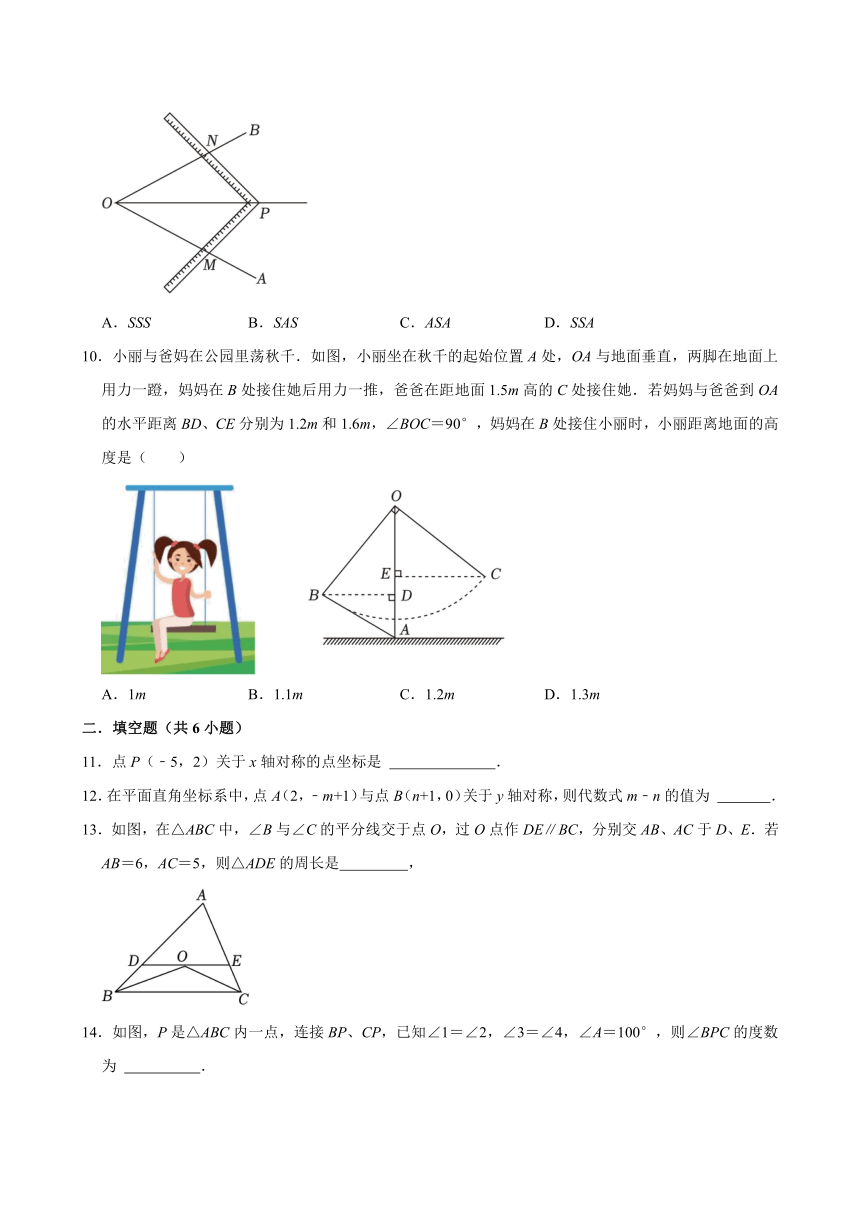
6.一副三角板按如图所示方式叠放在一起,则图中∠α的度数是( )
A.55° B.60° C.65° D.75°
7.如图,大建从A点出发沿直线前进8米到达B点后向左旋转的角度为α,再沿直线前进8米,到达点C后,又向左旋转α角度,照这样走下去,第一次回到出发地点时,他共走了72米,则每次旋转的角度α为( )
A.30° B.40° C.45° D.60°
8.如图,由9个完全相同的小正方形拼接而成的3×3网格,图形ABCD中各个顶点均为格点,设∠ABC=α,∠BCD=β,∠BAD=γ,则α﹣β﹣γ的值为( )
A.30° B.45° C.60° D.75°
9.工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA、OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与M、N重合,得到∠AOB的平分线OP,做法中用到三角形全等判定方法是( )
A.SSS B.SAS C.ASA D.SSA
10.小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在B处接住她后用力一推,爸爸在距地面1.5m高的C处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.2m和1.6m,∠BOC=90°,妈妈在B处接住小丽时,小丽距离地面的高度是( )
A.1m B.1.1m C.1.2m D.1.3m
二.填空题(共6小题)
11.点P(﹣5,2)关于x轴对称的点坐标是 .
12.在平面直角坐标系中,点A(2,﹣m+1)与点B(n+1,0)关于y轴对称,则代数式m﹣n的值为 .
13.如图,在△ABC中,∠B与∠C的平分线交于点O,过O点作DE∥BC,分别交AB、AC于D、E.若AB=6,AC=5,则△ADE的周长是 ,
14.如图,P是△ABC内一点,连接BP、CP,已知∠1=∠2,∠3=∠4,∠A=100°,则∠BPC的度数为 .
15.当三角形中一个内角α是另一个内角的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为42°,那么这个“特征角”α的度数为 .
16.已知如图:AC=CE,且∠ACE=90°,AB⊥BD于B,ED⊥BD于D,BC=2,CD=3.连接AD,AE.则图中阴影部分的面积为 .
三.解答题(共7小题)
17.已知△ABC中:
(1)∠A﹣∠B=20°,∠C=2∠B,求∠A、∠B、∠C的度数.
(2)a,b,c,是三角形的三边长,且a,b,c,都是整数.化简:|a﹣b+c|+|c﹣a﹣b|﹣|a+b|.
18.图①、图②均是4×4的正方形网格.每个小正方形的边长均为1.每个小正方形的顶点叫做格点,线段AB的端点均在格点上.只用无刻度的直尺,在给定的网格中按要求画图.所画图形的顶点均在格点上.不要求写出画法,并保留作图痕迹.
(1)在图①中画一个等腰三角形ABC,使其面积为2;
(2)在图②中画一个四边形ABDE,使其是轴对称图形且面积为3.
19.如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.若∠BAE=40°.求∠C的度数.
20.如图,在△ABC中,BD是AC边上的高,∠A=70°.
(1)求∠ABD的度数;
(2)若CE平分∠ACB交BD于点E,∠BEC=120°,求∠ACB的度数.
21.如图,在△ABC和△ADE中,∠C=∠E,∠1=∠2,AC=AE,AD、BC相交于点F.
(1)求证:△ABC≌△ADE;
(2)若AB∥DE,∠D=30°求∠AFB的度数.
22.在学习了全等三角形的知识后,一位同学进行了如下的探究,他发现:在一组对边平行且相等的四边形中,它的一组对角顶点到另一组对角顶点所连线段的距离存在着一定的数量关系.这位同学利用三角形全等证明了他的猜想,请根据他的想法与思路,完成以下作图与填空.
(1)如图,在四边形ABCD中,AB=CD,AB∥CD,连接AC,DF⊥AC于点F.利用尺规作图,过点B作AC的垂线,垂足为点E(不写作法,保留作图痕迹).
(2)在(1)问所作的图形中,求证:BE=DF.
证明:∵AB∥CD,
∴① .
∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS).
∴③ .
于是这位同学得到的结论是:在一组对边平行且相等的四边形中,④ .
23.已知AB∥CD,BP和CP分别平分∠ABC和∠BCD,点E,F分别在AB和CD上.
(1)如图1,EF过点P,且与AB垂直,求证:PE=PF;
(2)如图2,EF为过点P的任意一条线段,试猜想PE=PF还成立吗?请说明理由.
期中复习卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共10小题)
1.下列图形中,不是轴对称图形的是( )
A. B.
C. D.
【解答】解:选项A、C、D均能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
故选:B.
2.某三角形的三边长分别为3,6,x,则x不可能是( )
A.3.5 B.6 C.7.3 D.9.2
【解答】解:由题意得,6﹣3<x<3+6,即3<x<9,
∴x不可能是9.2,
故选:D.
3.已知A(﹣1,3),B(﹣1,﹣3),则下面结论中正确的是( )
A.A,B两点关于y轴对称 B.点A到y轴距离是3
C.点B到x轴距离是1 D.AB∥y轴
【解答】解:A.A,B两点关于x轴对称,故此选项不合题意;
B.点A到y轴距离是1,故此选项不合题意;
C.点B到x轴距离是3,故此选项不合题意;
D.AB∥y轴,故此选项符合题意.
故选:D.
4.将一副三角板如图摆放,则图中∠1的度数是( )
A.105° B.120° C.135° D.150°
【解答】解:如图,
由题可得∠2=180°﹣30°﹣45°=105°,
∵∠1和∠2是对顶角,
∴∠1=∠2,
∴∠1=105°,
故选:A.
5.如图,AD交BC于点O,∠BAD的平分线与△OCD的外角∠OCE的平分线交于点P,∠B=∠D,则下列说法不正确的是( )
A.∠PAO+∠PCD=90° B.
C.∠P=90°+∠D D.∠P=90°﹣2∠B
【解答】解:∵∠B+∠BAO+∠AOB=180°,∠D+∠BCD+∠COD=180°,∠AOB=∠COD,∠B=∠D,
∴∠BAO=∠BCD,
∵∠BCD+∠BCE=180°,
∴∠BAO+∠BCE=180°,
∵AP平分∠BAO,CP平分∠BCE,
∴∠PAB=∠PAO=∠BAO,∠PCE=∠BCE,
∴∠PAO+∠PCE=90°,故A选项不符合题意;
∠PAB=∠BCD,故B选项不符合题意;
延长AP交BC于点M,
∵∠APC=∠AMC+∠BCP,∠AMC=∠B+∠BAM,
∴∠APC=∠BAM+∠B+∠BCP,
∵∠B=∠D,∠BAP+∠BCP=∠PAO+∠PCE=90°,
∴∠APC=90°+∠D,故C选项不符合题意;
∴∠APC≠90°﹣2∠B,故D选项符合题意,
故选:D.
6.一副三角板按如图所示方式叠放在一起,则图中∠α的度数是( )
A.55° B.60° C.65° D.75°
【解答】解:由题意得:∠1=90°﹣60°=30°,
则∠α=45°+30°=75°,
故选:D.
7.如图,大建从A点出发沿直线前进8米到达B点后向左旋转的角度为α,再沿直线前进8米,到达点C后,又向左旋转α角度,照这样走下去,第一次回到出发地点时,他共走了72米,则每次旋转的角度α为( )
A.30° B.40° C.45° D.60°
【解答】解:∵72÷8=9,
∴360°÷9=40°.
∴每次旋转的角度α=40°.
故选:B.
8.如图,由9个完全相同的小正方形拼接而成的3×3网格,图形ABCD中各个顶点均为格点,设∠ABC=α,∠BCD=β,∠BAD=γ,则α﹣β﹣γ的值为( )
A.30° B.45° C.60° D.75°
【解答】
解:如图,BE=AG,∠BEC=∠AGB=90°,EC=GB,
∴△BEC≌△AGB(SAS),
∴∠ECB=∠GBA,
∵∠ECB+∠EBC=90°,
∴∠GBA+∠EBC=90°,
∴∠ABC=90°=α,
∵∠β+∠CBD=90°,∠CBD+∠ABD=90°,
∴∠ABD=β,
∵∠ADF=∠ABD+∠BAD=45°,
∴β+γ=45°,
∴α﹣β﹣γ=90°﹣45°=45°,
故选:B.
9.工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA、OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与M、N重合,得到∠AOB的平分线OP,做法中用到三角形全等判定方法是( )
A.SSS B.SAS C.ASA D.SSA
【解答】解:做法中用到的三角形全等的判定方法是SSS.
证明如下:
由题意得,PN=PM,
在△ONP和△OMP中,
,
∴△ONP≌△OMP(SSS),
∴∠NOP=∠MOP,
∴OP为∠AOB的平分线.
故选:A.
10.小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在B处接住她后用力一推,爸爸在距地面1.5m高的C处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.2m和1.6m,∠BOC=90°,妈妈在B处接住小丽时,小丽距离地面的高度是( )
A.1m B.1.1m C.1.2m D.1.3m
【解答】解:依题意结合图形可知:OB=OC,BD=1.2m,CE=1.6cm,CE⊥OA,BD⊥OA,OA与地面垂直,C处距地面1.5m高,∠BOC=90°,
∴∠OEC=∠BDO=90°,AE=1.5m,
∴∠COE+∠C=90°,
∴∠COE+∠BOD=90°,
∴∠BOD=∠C,
在△BOD和△OCE中,
,
∴△BOD≌△OCE(AAS),
∴BD=OE=1.2m,OD=CE=1.6cm,
∴OA=OE+AE=1.2+1.5=2.7(m),
∴AD=OA﹣OD=2.7﹣1.6=1.1(m),
即妈妈在B处接住小丽时,小丽距离地面的高度是1.1m,
故选:B.
二.填空题(共6小题)
11.点P(﹣5,2)关于x轴对称的点坐标是 (﹣5,﹣2) .
【解答】解:点P(﹣5,2)关于x轴对称的点坐标是(﹣5,﹣2),
故答案为:(﹣5,﹣2).
12.在平面直角坐标系中,点A(2,﹣m+1)与点B(n+1,0)关于y轴对称,则代数式m﹣n的值为 4 .
【解答】解:∵点A(2,﹣m+1)与点B(n+1,0)关于y轴对称,
∴n+1=﹣2,﹣m+1=0,
∴m=1,n=﹣3,
∴m﹣n=1﹣(﹣3)=4.
故答案为:4.
13.如图,在△ABC中,∠B与∠C的平分线交于点O,过O点作DE∥BC,分别交AB、AC于D、E.若AB=6,AC=5,则△ADE的周长是 11 ,
【解答】解:∵BO平分∠ABC,
∴∠DBO=∠CBO,
∵DE∥BC,
∴∠DOB=∠CBO,
∴∠DBO=∠DOB,
∴BD=DO,
同理EO=CE,
∴△ADE的周长是AE+AD+DE
=AD+DO+EO+AE
=AD+BD+AE+CE
=AB+AC
=6+5
=11,
故答案为:11.
14.如图,P是△ABC内一点,连接BP、CP,已知∠1=∠2,∠3=∠4,∠A=100°,则∠BPC的度数为 140 .
【解答】解:在△ABC中,∠A+∠ABC+∠ACB=180°,
∵∠A=100°,
∴∠ABC+∠ACB=180°﹣100°=80°,
即∠1+∠2+∠3+∠4=80°,
∵∠1=∠2,∠3=∠4,
∴2∠2+2∠4=80°,
∴∠2+∠4=40°,
在△BPC中,∠BPC+∠2+∠4=180°,
∴∠BPC=140°,
故答案为:140.
15.当三角形中一个内角α是另一个内角的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为42°,那么这个“特征角”α的度数为 42°或84°或92° .
【解答】解:当内角α是42°时,三角形的一个内角为42°÷2=21°,
∵42°+21°<180°,
∴∠α=42°符合题意;
当内角α是42°的两倍时,∠α=42°×2=84°,
∵42°+84°=126°<180°,
∴∠α=84°符合题意;
当内角α是第三个角的两倍时,设∠α=x°,则第三个角的速度为x°,
依题意得:42+x+x=180,
解得:x=92,
∴∠α=92°.
综上所述,∠α的度数为42°或84°或92°.
故答案为:42°或84°或92°.
16.已知如图:AC=CE,且∠ACE=90°,AB⊥BD于B,ED⊥BD于D,BC=2,CD=3.连接AD,AE.则图中阴影部分的面积为 5 .
【解答】解:∵∠ACE=90°,AB⊥BD于B,ED⊥BD于D,
∴∠ACE=∠B=∠CDE=90°,
∴∠BAC+∠BCA=∠BCA+∠DCE=90°,
∴∠BAC=∠DCE,
在△BAC和△DCE中,
,
∴△BAC≌△DCE(AAS),
∴DE=BC=2,
∴,
故答案为:5.
三.解答题(共7小题)
17.已知△ABC中:
(1)∠A﹣∠B=20°,∠C=2∠B,求∠A、∠B、∠C的度数.
(2)a,b,c,是三角形的三边长,且a,b,c,都是整数.化简:|a﹣b+c|+|c﹣a﹣b|﹣|a+b|.
【解答】解:(1)设∠B=x°,
∵∠A﹣∠B=20°,∠C=2∠B,
∴∠A=∠B+20°=x°+20°,∠C=2∠B=2x°,
∵∠A+∠B+∠C=180°,
∴x+20+x+2x=180,
解得:x=40,
∴∠A=60°,∠B=40°,∠C=80°;
(2)∵a,b,c是三角形的三边长,
∴a+c>b,c﹣a<b,a+b>0,
∴a﹣b+c>0,c﹣a﹣b<0,
∴|a﹣b+c|+|c﹣a﹣b|﹣|a+b|
=a﹣b+c+a+b﹣c﹣a﹣b
=a﹣b.
18.图①、图②均是4×4的正方形网格.每个小正方形的边长均为1.每个小正方形的顶点叫做格点,线段AB的端点均在格点上.只用无刻度的直尺,在给定的网格中按要求画图.所画图形的顶点均在格点上.不要求写出画法,并保留作图痕迹.
(1)在图①中画一个等腰三角形ABC,使其面积为2;
(2)在图②中画一个四边形ABDE,使其是轴对称图形且面积为3.
【解答】解:(1)如图,∵BC=2,AD=2,
∴,
∵AB=AC,
∴△ABC即为所求;
(2)如图,∵,
∴四边形ABDE即为所求.
19.如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.若∠BAE=40°.求∠C的度数.
【解答】解:∵EF垂直平分AC,
∴EA=EC,
∵AD⊥BC,BD=DE,
∴AD是BE的垂直平分线,
∴AB=AE,
∵∠BAE=40°,
∴∠B=∠AEB==70°,
∴∠C+∠EAC=70°,
∵EA=EC,
∴∠C=∠EAC=35°,
∴∠C的度数为35°.
20.如图,在△ABC中,BD是AC边上的高,∠A=70°.
(1)求∠ABD的度数;
(2)若CE平分∠ACB交BD于点E,∠BEC=120°,求∠ACB的度数.
【解答】解:(1)在△ABC中,
∵BD是AC边上的高,
∴∠ADB=∠BDC=90°,
∵∠A=70°,
∴∠ABD=180°﹣∠BDA﹣∠A=20°;
(2)在△EDC中,
∵∠BEC=∠BDC+∠DCE,且∠BEC=120°,∠BDC=90°,
∴∠DCE=30°,
∵CE平分∠ACB,
∴∠DCB=2∠DCE=60°,
∴∠ACB=60°.
21.如图,在△ABC和△ADE中,∠C=∠E,∠1=∠2,AC=AE,AD、BC相交于点F.
(1)求证:△ABC≌△ADE;
(2)若AB∥DE,∠D=30°求∠AFB的度数.
【解答】(1)证明:∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
∴∠CAB=∠EAD,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(AAS);
(2)解:∵AB∥DE,∠D=30°,
∴∠1=∠D=30°,
∵△ABC≌△ADE,
∴∠B=∠D=30°,
∴∠AFB=180°﹣∠3﹣∠B=180°﹣30°﹣30°=120°.
22.在学习了全等三角形的知识后,一位同学进行了如下的探究,他发现:在一组对边平行且相等的四边形中,它的一组对角顶点到另一组对角顶点所连线段的距离存在着一定的数量关系.这位同学利用三角形全等证明了他的猜想,请根据他的想法与思路,完成以下作图与填空.
(1)如图,在四边形ABCD中,AB=CD,AB∥CD,连接AC,DF⊥AC于点F.利用尺规作图,过点B作AC的垂线,垂足为点E(不写作法,保留作图痕迹).
(2)在(1)问所作的图形中,求证:BE=DF.
证明:∵AB∥CD,
∴① ∠BAE=∠DCF .
∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS).
∴③ BE=DF .
于是这位同学得到的结论是:在一组对边平行且相等的四边形中,④ 相对的顶点到对角线的距离相等 .
【解答】(1)解:由题意,作图如下.
(2)证明:∵AB∥CD,
∴①∠BAE=∠DCF.
∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°.
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS).
∴③BE=DF.
于是这位同学得到的结论是:在一组对边平行且相等的四边形中,④相对的顶点到对角线的距离相等.
故答案为:①∠BAE=∠DCF;②∠AEB=∠CFD;③BE=DF;④相对的顶点到对角线的距离相等.
23.已知AB∥CD,BP和CP分别平分∠ABC和∠BCD,点E,F分别在AB和CD上.
(1)如图1,EF过点P,且与AB垂直,求证:PE=PF;
(2)如图2,EF为过点P的任意一条线段,试猜想PE=PF还成立吗?请说明理由.
【解答】(1)证明:如图,过点P作PM⊥BC于点M,
∵AB∥CD,EF⊥AB,
∴EF⊥CD.
∵BP和CP分别是∠ABC和∠BCD的平分线,
且PM⊥BC,EF⊥AB,EF⊥CD,
∴PE=PM,PM=PF.
∴PE=PF.
(2)解:PE=PF成立.理由如下:
如图,过点P作GH⊥AB于点G,交CD于点H,
∵AB∥CD,
∴PG⊥AB,PH⊥CD,
∴∠PGE=∠PHF=90°,
由(1)得PG=PH,在△PGE和△PHF中,
∵
∴△PGE≌△PHF(ASA),
∴PE=PF.
一.选择题(共10小题)
1.下列图形中,不是轴对称图形的是( )
A. B.
C. D.
2.某三角形的三边长分别为3,6,x,则x不可能是( )
A.3.5 B.6 C.7.3 D.9.2
3.已知A(﹣1,3),B(﹣1,﹣3),则下面结论中正确的是( )
A.A,B两点关于y轴对称 B.点A到y轴距离是3
C.点B到x轴距离是1 D.AB∥y轴
4.将一副三角板如图摆放,则图中∠1的度数是( )
A.105° B.120° C.135° D.150°
5.如图,AD交BC于点O,∠BAD的平分线与△OCD的外角∠OCE的平分线交于点P,∠B=∠D,则下列说法不正确的是( )
A.∠PAO+∠PCD=90° B.
C.∠P=90°+∠D D.∠P=90°﹣2∠B
6.一副三角板按如图所示方式叠放在一起,则图中∠α的度数是( )
A.55° B.60° C.65° D.75°
7.如图,大建从A点出发沿直线前进8米到达B点后向左旋转的角度为α,再沿直线前进8米,到达点C后,又向左旋转α角度,照这样走下去,第一次回到出发地点时,他共走了72米,则每次旋转的角度α为( )
A.30° B.40° C.45° D.60°
8.如图,由9个完全相同的小正方形拼接而成的3×3网格,图形ABCD中各个顶点均为格点,设∠ABC=α,∠BCD=β,∠BAD=γ,则α﹣β﹣γ的值为( )
A.30° B.45° C.60° D.75°
9.工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA、OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与M、N重合,得到∠AOB的平分线OP,做法中用到三角形全等判定方法是( )
A.SSS B.SAS C.ASA D.SSA
10.小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在B处接住她后用力一推,爸爸在距地面1.5m高的C处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.2m和1.6m,∠BOC=90°,妈妈在B处接住小丽时,小丽距离地面的高度是( )
A.1m B.1.1m C.1.2m D.1.3m
二.填空题(共6小题)
11.点P(﹣5,2)关于x轴对称的点坐标是 .
12.在平面直角坐标系中,点A(2,﹣m+1)与点B(n+1,0)关于y轴对称,则代数式m﹣n的值为 .
13.如图,在△ABC中,∠B与∠C的平分线交于点O,过O点作DE∥BC,分别交AB、AC于D、E.若AB=6,AC=5,则△ADE的周长是 ,
14.如图,P是△ABC内一点,连接BP、CP,已知∠1=∠2,∠3=∠4,∠A=100°,则∠BPC的度数为 .
15.当三角形中一个内角α是另一个内角的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为42°,那么这个“特征角”α的度数为 .
16.已知如图:AC=CE,且∠ACE=90°,AB⊥BD于B,ED⊥BD于D,BC=2,CD=3.连接AD,AE.则图中阴影部分的面积为 .
三.解答题(共7小题)
17.已知△ABC中:
(1)∠A﹣∠B=20°,∠C=2∠B,求∠A、∠B、∠C的度数.
(2)a,b,c,是三角形的三边长,且a,b,c,都是整数.化简:|a﹣b+c|+|c﹣a﹣b|﹣|a+b|.
18.图①、图②均是4×4的正方形网格.每个小正方形的边长均为1.每个小正方形的顶点叫做格点,线段AB的端点均在格点上.只用无刻度的直尺,在给定的网格中按要求画图.所画图形的顶点均在格点上.不要求写出画法,并保留作图痕迹.
(1)在图①中画一个等腰三角形ABC,使其面积为2;
(2)在图②中画一个四边形ABDE,使其是轴对称图形且面积为3.
19.如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.若∠BAE=40°.求∠C的度数.
20.如图,在△ABC中,BD是AC边上的高,∠A=70°.
(1)求∠ABD的度数;
(2)若CE平分∠ACB交BD于点E,∠BEC=120°,求∠ACB的度数.
21.如图,在△ABC和△ADE中,∠C=∠E,∠1=∠2,AC=AE,AD、BC相交于点F.
(1)求证:△ABC≌△ADE;
(2)若AB∥DE,∠D=30°求∠AFB的度数.
22.在学习了全等三角形的知识后,一位同学进行了如下的探究,他发现:在一组对边平行且相等的四边形中,它的一组对角顶点到另一组对角顶点所连线段的距离存在着一定的数量关系.这位同学利用三角形全等证明了他的猜想,请根据他的想法与思路,完成以下作图与填空.
(1)如图,在四边形ABCD中,AB=CD,AB∥CD,连接AC,DF⊥AC于点F.利用尺规作图,过点B作AC的垂线,垂足为点E(不写作法,保留作图痕迹).
(2)在(1)问所作的图形中,求证:BE=DF.
证明:∵AB∥CD,
∴① .
∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS).
∴③ .
于是这位同学得到的结论是:在一组对边平行且相等的四边形中,④ .
23.已知AB∥CD,BP和CP分别平分∠ABC和∠BCD,点E,F分别在AB和CD上.
(1)如图1,EF过点P,且与AB垂直,求证:PE=PF;
(2)如图2,EF为过点P的任意一条线段,试猜想PE=PF还成立吗?请说明理由.
期中复习卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共10小题)
1.下列图形中,不是轴对称图形的是( )
A. B.
C. D.
【解答】解:选项A、C、D均能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形,
选项B不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形,
故选:B.
2.某三角形的三边长分别为3,6,x,则x不可能是( )
A.3.5 B.6 C.7.3 D.9.2
【解答】解:由题意得,6﹣3<x<3+6,即3<x<9,
∴x不可能是9.2,
故选:D.
3.已知A(﹣1,3),B(﹣1,﹣3),则下面结论中正确的是( )
A.A,B两点关于y轴对称 B.点A到y轴距离是3
C.点B到x轴距离是1 D.AB∥y轴
【解答】解:A.A,B两点关于x轴对称,故此选项不合题意;
B.点A到y轴距离是1,故此选项不合题意;
C.点B到x轴距离是3,故此选项不合题意;
D.AB∥y轴,故此选项符合题意.
故选:D.
4.将一副三角板如图摆放,则图中∠1的度数是( )
A.105° B.120° C.135° D.150°
【解答】解:如图,
由题可得∠2=180°﹣30°﹣45°=105°,
∵∠1和∠2是对顶角,
∴∠1=∠2,
∴∠1=105°,
故选:A.
5.如图,AD交BC于点O,∠BAD的平分线与△OCD的外角∠OCE的平分线交于点P,∠B=∠D,则下列说法不正确的是( )
A.∠PAO+∠PCD=90° B.
C.∠P=90°+∠D D.∠P=90°﹣2∠B
【解答】解:∵∠B+∠BAO+∠AOB=180°,∠D+∠BCD+∠COD=180°,∠AOB=∠COD,∠B=∠D,
∴∠BAO=∠BCD,
∵∠BCD+∠BCE=180°,
∴∠BAO+∠BCE=180°,
∵AP平分∠BAO,CP平分∠BCE,
∴∠PAB=∠PAO=∠BAO,∠PCE=∠BCE,
∴∠PAO+∠PCE=90°,故A选项不符合题意;
∠PAB=∠BCD,故B选项不符合题意;
延长AP交BC于点M,
∵∠APC=∠AMC+∠BCP,∠AMC=∠B+∠BAM,
∴∠APC=∠BAM+∠B+∠BCP,
∵∠B=∠D,∠BAP+∠BCP=∠PAO+∠PCE=90°,
∴∠APC=90°+∠D,故C选项不符合题意;
∴∠APC≠90°﹣2∠B,故D选项符合题意,
故选:D.
6.一副三角板按如图所示方式叠放在一起,则图中∠α的度数是( )
A.55° B.60° C.65° D.75°
【解答】解:由题意得:∠1=90°﹣60°=30°,
则∠α=45°+30°=75°,
故选:D.
7.如图,大建从A点出发沿直线前进8米到达B点后向左旋转的角度为α,再沿直线前进8米,到达点C后,又向左旋转α角度,照这样走下去,第一次回到出发地点时,他共走了72米,则每次旋转的角度α为( )
A.30° B.40° C.45° D.60°
【解答】解:∵72÷8=9,
∴360°÷9=40°.
∴每次旋转的角度α=40°.
故选:B.
8.如图,由9个完全相同的小正方形拼接而成的3×3网格,图形ABCD中各个顶点均为格点,设∠ABC=α,∠BCD=β,∠BAD=γ,则α﹣β﹣γ的值为( )
A.30° B.45° C.60° D.75°
【解答】
解:如图,BE=AG,∠BEC=∠AGB=90°,EC=GB,
∴△BEC≌△AGB(SAS),
∴∠ECB=∠GBA,
∵∠ECB+∠EBC=90°,
∴∠GBA+∠EBC=90°,
∴∠ABC=90°=α,
∵∠β+∠CBD=90°,∠CBD+∠ABD=90°,
∴∠ABD=β,
∵∠ADF=∠ABD+∠BAD=45°,
∴β+γ=45°,
∴α﹣β﹣γ=90°﹣45°=45°,
故选:B.
9.工人师傅常用角尺平分一个任意角,做法是:如图在∠AOB的边OA、OB上分别取OM=ON,移动角尺,使角尺的两边相同的刻度分别与M、N重合,得到∠AOB的平分线OP,做法中用到三角形全等判定方法是( )
A.SSS B.SAS C.ASA D.SSA
【解答】解:做法中用到的三角形全等的判定方法是SSS.
证明如下:
由题意得,PN=PM,
在△ONP和△OMP中,
,
∴△ONP≌△OMP(SSS),
∴∠NOP=∠MOP,
∴OP为∠AOB的平分线.
故选:A.
10.小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在B处接住她后用力一推,爸爸在距地面1.5m高的C处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.2m和1.6m,∠BOC=90°,妈妈在B处接住小丽时,小丽距离地面的高度是( )
A.1m B.1.1m C.1.2m D.1.3m
【解答】解:依题意结合图形可知:OB=OC,BD=1.2m,CE=1.6cm,CE⊥OA,BD⊥OA,OA与地面垂直,C处距地面1.5m高,∠BOC=90°,
∴∠OEC=∠BDO=90°,AE=1.5m,
∴∠COE+∠C=90°,
∴∠COE+∠BOD=90°,
∴∠BOD=∠C,
在△BOD和△OCE中,
,
∴△BOD≌△OCE(AAS),
∴BD=OE=1.2m,OD=CE=1.6cm,
∴OA=OE+AE=1.2+1.5=2.7(m),
∴AD=OA﹣OD=2.7﹣1.6=1.1(m),
即妈妈在B处接住小丽时,小丽距离地面的高度是1.1m,
故选:B.
二.填空题(共6小题)
11.点P(﹣5,2)关于x轴对称的点坐标是 (﹣5,﹣2) .
【解答】解:点P(﹣5,2)关于x轴对称的点坐标是(﹣5,﹣2),
故答案为:(﹣5,﹣2).
12.在平面直角坐标系中,点A(2,﹣m+1)与点B(n+1,0)关于y轴对称,则代数式m﹣n的值为 4 .
【解答】解:∵点A(2,﹣m+1)与点B(n+1,0)关于y轴对称,
∴n+1=﹣2,﹣m+1=0,
∴m=1,n=﹣3,
∴m﹣n=1﹣(﹣3)=4.
故答案为:4.
13.如图,在△ABC中,∠B与∠C的平分线交于点O,过O点作DE∥BC,分别交AB、AC于D、E.若AB=6,AC=5,则△ADE的周长是 11 ,
【解答】解:∵BO平分∠ABC,
∴∠DBO=∠CBO,
∵DE∥BC,
∴∠DOB=∠CBO,
∴∠DBO=∠DOB,
∴BD=DO,
同理EO=CE,
∴△ADE的周长是AE+AD+DE
=AD+DO+EO+AE
=AD+BD+AE+CE
=AB+AC
=6+5
=11,
故答案为:11.
14.如图,P是△ABC内一点,连接BP、CP,已知∠1=∠2,∠3=∠4,∠A=100°,则∠BPC的度数为 140 .
【解答】解:在△ABC中,∠A+∠ABC+∠ACB=180°,
∵∠A=100°,
∴∠ABC+∠ACB=180°﹣100°=80°,
即∠1+∠2+∠3+∠4=80°,
∵∠1=∠2,∠3=∠4,
∴2∠2+2∠4=80°,
∴∠2+∠4=40°,
在△BPC中,∠BPC+∠2+∠4=180°,
∴∠BPC=140°,
故答案为:140.
15.当三角形中一个内角α是另一个内角的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为42°,那么这个“特征角”α的度数为 42°或84°或92° .
【解答】解:当内角α是42°时,三角形的一个内角为42°÷2=21°,
∵42°+21°<180°,
∴∠α=42°符合题意;
当内角α是42°的两倍时,∠α=42°×2=84°,
∵42°+84°=126°<180°,
∴∠α=84°符合题意;
当内角α是第三个角的两倍时,设∠α=x°,则第三个角的速度为x°,
依题意得:42+x+x=180,
解得:x=92,
∴∠α=92°.
综上所述,∠α的度数为42°或84°或92°.
故答案为:42°或84°或92°.
16.已知如图:AC=CE,且∠ACE=90°,AB⊥BD于B,ED⊥BD于D,BC=2,CD=3.连接AD,AE.则图中阴影部分的面积为 5 .
【解答】解:∵∠ACE=90°,AB⊥BD于B,ED⊥BD于D,
∴∠ACE=∠B=∠CDE=90°,
∴∠BAC+∠BCA=∠BCA+∠DCE=90°,
∴∠BAC=∠DCE,
在△BAC和△DCE中,
,
∴△BAC≌△DCE(AAS),
∴DE=BC=2,
∴,
故答案为:5.
三.解答题(共7小题)
17.已知△ABC中:
(1)∠A﹣∠B=20°,∠C=2∠B,求∠A、∠B、∠C的度数.
(2)a,b,c,是三角形的三边长,且a,b,c,都是整数.化简:|a﹣b+c|+|c﹣a﹣b|﹣|a+b|.
【解答】解:(1)设∠B=x°,
∵∠A﹣∠B=20°,∠C=2∠B,
∴∠A=∠B+20°=x°+20°,∠C=2∠B=2x°,
∵∠A+∠B+∠C=180°,
∴x+20+x+2x=180,
解得:x=40,
∴∠A=60°,∠B=40°,∠C=80°;
(2)∵a,b,c是三角形的三边长,
∴a+c>b,c﹣a<b,a+b>0,
∴a﹣b+c>0,c﹣a﹣b<0,
∴|a﹣b+c|+|c﹣a﹣b|﹣|a+b|
=a﹣b+c+a+b﹣c﹣a﹣b
=a﹣b.
18.图①、图②均是4×4的正方形网格.每个小正方形的边长均为1.每个小正方形的顶点叫做格点,线段AB的端点均在格点上.只用无刻度的直尺,在给定的网格中按要求画图.所画图形的顶点均在格点上.不要求写出画法,并保留作图痕迹.
(1)在图①中画一个等腰三角形ABC,使其面积为2;
(2)在图②中画一个四边形ABDE,使其是轴对称图形且面积为3.
【解答】解:(1)如图,∵BC=2,AD=2,
∴,
∵AB=AC,
∴△ABC即为所求;
(2)如图,∵,
∴四边形ABDE即为所求.
19.如图,在△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE,连接AE.若∠BAE=40°.求∠C的度数.
【解答】解:∵EF垂直平分AC,
∴EA=EC,
∵AD⊥BC,BD=DE,
∴AD是BE的垂直平分线,
∴AB=AE,
∵∠BAE=40°,
∴∠B=∠AEB==70°,
∴∠C+∠EAC=70°,
∵EA=EC,
∴∠C=∠EAC=35°,
∴∠C的度数为35°.
20.如图,在△ABC中,BD是AC边上的高,∠A=70°.
(1)求∠ABD的度数;
(2)若CE平分∠ACB交BD于点E,∠BEC=120°,求∠ACB的度数.
【解答】解:(1)在△ABC中,
∵BD是AC边上的高,
∴∠ADB=∠BDC=90°,
∵∠A=70°,
∴∠ABD=180°﹣∠BDA﹣∠A=20°;
(2)在△EDC中,
∵∠BEC=∠BDC+∠DCE,且∠BEC=120°,∠BDC=90°,
∴∠DCE=30°,
∵CE平分∠ACB,
∴∠DCB=2∠DCE=60°,
∴∠ACB=60°.
21.如图,在△ABC和△ADE中,∠C=∠E,∠1=∠2,AC=AE,AD、BC相交于点F.
(1)求证:△ABC≌△ADE;
(2)若AB∥DE,∠D=30°求∠AFB的度数.
【解答】(1)证明:∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
∴∠CAB=∠EAD,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(AAS);
(2)解:∵AB∥DE,∠D=30°,
∴∠1=∠D=30°,
∵△ABC≌△ADE,
∴∠B=∠D=30°,
∴∠AFB=180°﹣∠3﹣∠B=180°﹣30°﹣30°=120°.
22.在学习了全等三角形的知识后,一位同学进行了如下的探究,他发现:在一组对边平行且相等的四边形中,它的一组对角顶点到另一组对角顶点所连线段的距离存在着一定的数量关系.这位同学利用三角形全等证明了他的猜想,请根据他的想法与思路,完成以下作图与填空.
(1)如图,在四边形ABCD中,AB=CD,AB∥CD,连接AC,DF⊥AC于点F.利用尺规作图,过点B作AC的垂线,垂足为点E(不写作法,保留作图痕迹).
(2)在(1)问所作的图形中,求证:BE=DF.
证明:∵AB∥CD,
∴① ∠BAE=∠DCF .
∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS).
∴③ BE=DF .
于是这位同学得到的结论是:在一组对边平行且相等的四边形中,④ 相对的顶点到对角线的距离相等 .
【解答】(1)解:由题意,作图如下.
(2)证明:∵AB∥CD,
∴①∠BAE=∠DCF.
∵BE⊥AC,DF⊥AC,
∴∠AEB=∠CFD=90°.
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS).
∴③BE=DF.
于是这位同学得到的结论是:在一组对边平行且相等的四边形中,④相对的顶点到对角线的距离相等.
故答案为:①∠BAE=∠DCF;②∠AEB=∠CFD;③BE=DF;④相对的顶点到对角线的距离相等.
23.已知AB∥CD,BP和CP分别平分∠ABC和∠BCD,点E,F分别在AB和CD上.
(1)如图1,EF过点P,且与AB垂直,求证:PE=PF;
(2)如图2,EF为过点P的任意一条线段,试猜想PE=PF还成立吗?请说明理由.
【解答】(1)证明:如图,过点P作PM⊥BC于点M,
∵AB∥CD,EF⊥AB,
∴EF⊥CD.
∵BP和CP分别是∠ABC和∠BCD的平分线,
且PM⊥BC,EF⊥AB,EF⊥CD,
∴PE=PM,PM=PF.
∴PE=PF.
(2)解:PE=PF成立.理由如下:
如图,过点P作GH⊥AB于点G,交CD于点H,
∵AB∥CD,
∴PG⊥AB,PH⊥CD,
∴∠PGE=∠PHF=90°,
由(1)得PG=PH,在△PGE和△PHF中,
∵
∴△PGE≌△PHF(ASA),
∴PE=PF.
同课章节目录
