2024—2025学年苏科版数学九年级上册 第1-2章阶段检测卷(含详解)
文档属性
| 名称 | 2024—2025学年苏科版数学九年级上册 第1-2章阶段检测卷(含详解) |

|
|
| 格式 | docx | ||
| 文件大小 | 377.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-02 00:00:00 | ||
图片预览




文档简介
第1-2章阶段检测卷-2024-2025学年数学九年级上册苏科版
一.选择题(共8小题)
1.(2023秋 朝阳区校级期末)下列关于x的方程中,一定是一元二次方程的为( )
A.x2+2xy+y2=0 B.x2﹣2x+3=0
C. D.ax2+bx+c=0
2.(2023秋 方城县期末)关于x的一元二次方程kx2+4x﹣2=0有实数根,则k的取值范围是( )
A.k≥﹣2 B.k>﹣2且k≠0 C.k≥﹣2且k≠0 D.k≤﹣2
3.(2024春 瑶海区期中)已知一元二次方程x2﹣x﹣2=0的一个根为m,则2023﹣m2+m的值是( )
A.2020 B.2021 C.2023 D.2025
4.(2024春 慈溪市期末)杭州亚运会吉祥物深受大家喜爱.某商户3月份销售吉祥物“宸宸”摆件为10万个,5月份销售11.5万个.设该摆件销售量的月平均增长率为x(x>0),则可列方程为( )
A.10(1+x)2=11.5 B.10(1+2x)=11.5
C.10x2=11.5 D.11.5(1﹣x)2=10
5.(2024 大庆二模)三角形的外心是( )
A.三边上的高线的交点
B.三边中线的交点
C.三边垂直平分线的交点
D.三个内角平分线的交点
6.(2024 雁塔区校级四模)如图,四边形ABCD内接于⊙O,已知点C为的中点,若∠A=50°,则∠CBD的度数为( )
A.50° B.40° C.30° D.25°
7.(2024秋 鄞州区校级月考)如图,直径AB=12的半圆绕点B按顺时针方向旋转30°,此时A到了点A′的位置,则图中阴影部分的面积是( )
A.2π B.3π C.4π D.12π
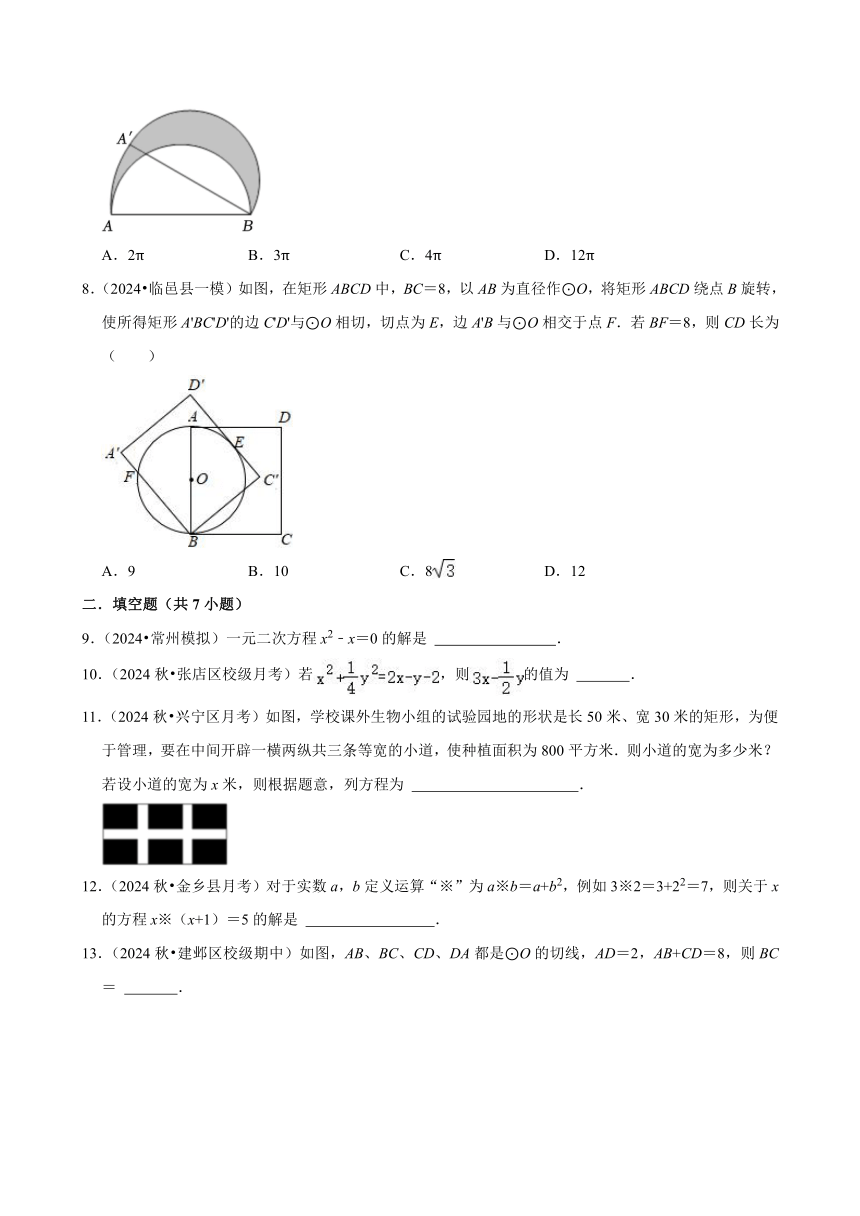
8.(2024 临邑县一模)如图,在矩形ABCD中,BC=8,以AB为直径作⊙O,将矩形ABCD绕点B旋转,使所得矩形A'BC'D'的边C'D'与⊙O相切,切点为E,边A'B与⊙O相交于点F.若BF=8,则CD长为( )
A.9 B.10 C.8 D.12
二.填空题(共7小题)
9.(2024 常州模拟)一元二次方程x2﹣x=0的解是 .
10.(2024秋 张店区校级月考)若,则的值为 .
11.(2024秋 兴宁区月考)如图,学校课外生物小组的试验园地的形状是长50米、宽30米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为800平方米.则小道的宽为多少米?若设小道的宽为x米,则根据题意,列方程为 .
12.(2024秋 金乡县月考)对于实数a,b定义运算“※”为a※b=a+b2,例如3※2=3+22=7,则关于x的方程x※(x+1)=5的解是 .
13.(2024秋 建邺区校级期中)如图,AB、BC、CD、DA都是⊙O的切线,AD=2,AB+CD=8,则BC= .
14.(2024 盐城三模)圆在中式建筑中有着广泛的应用.如图,某园林中圆弧形门洞的顶端到地面的高度为2.8m,地面入口的宽度为1m,门枕的高度为0.3m,则该圆弧所在圆的半径为 m.
15.(2024秋 工业园区校级月考)如图,AB是⊙O的直径,∠CAB=40°,则∠B= .
三.解答题(共7小题)
16.(2024秋 龙海区校级月考)解方程:
(1)x2﹣2x+1=3;
(2)x2﹣5x+6=0.
17.(2024秋 通许县期中)已知关于x的方程x2﹣(m+1)x﹣1=0.
(1)求证:无论m取什么实数值,方程总有两个不相等的实数根;
(2)若该方程的两个根互为相反数,求m的值.
18.(2024秋 邗江区校级月考)烟花三月下扬州,东关街区人如流.东关街某店铺以每件45元的批发价购进一批长毛绒玩偶盲盒,以每件68元的价格出售,一经开售,深受游客喜爱.经统计,第一周该盲盒的销售量为256件,第三周的销售量达到400件.
(1)求该盲盒第一周到第三周销售量的周平均增长率;
(2)从第四周起,店铺经营者决定采用降价促销的方式回馈游客,经试验,发现该盲盒每降价1元,周销售量就会增加20件.当该盲盒售价为多少元时,周销售利润达8400元?
19.(2024 济南模拟)(1)尺规作图,作出△ABC的外接圆(不写作图过程,但保留作图痕迹);
(2)若AB=,∠B=45°,BC=6,求△ABC外接圆的半径长.
20.(2024 烟台一模)如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.
(1)求证:BD为圆的直径;
(2)过点C作CF∥AD交AB的延长线于点F,若AC=AD,BF=2,求此圆半径的长.
21.(2023秋 武胜县期末)HUAWEIMate60Pro于8月29日上市,该系列完成了核心技术领域从0到1的跃迁,让无数国人为之自豪并被赞誉为“争气机”.手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量.圆弧对应的弦AB长80mm,弓形高CD长14mm求半径OA的长.
22.(2024 海陵区一模)学习下面方框内的内容,并解答下列问题:
小明在反思学习时,发现解决下列3个问题时都用到了同一种数学思想方法: 问题1:若a﹣2b=3,求2a﹣4b+1的值. 解决思路:2a﹣4b+1=2(a﹣2b)+1=2×3+1=7. 问题2:如图1,分别以△ABC的3个顶点为圆心,2为半径画圆,求图中3块阴影面积之和. 解决思路:将3块阴影扇形拼成一个半径为2的半圆,则阴影面积为2π. 问题3:已知a2+b2=3ab(a>b>0),求的值. 解题思路:对已知条件进行恒等变形,a2+b2+2ab=5ab,(a+b)2=5ab,因为a>b>0,所以,类似可以得到a﹣b=….
问题:
(1)方框内3个问题的解决都用到了 的数学思想方法(从下列选项中选一个);
A.分类讨论
B.数形结合
C.整体
D.从特殊到一般
(2)方框内问题3中的值为 ;
(3)如图2,已知⊙O的半径为5,AB、CD是⊙O的弦,且AB=8,CD=6,求与的长度之和.
第1-2章阶段检测卷-2024-2025学年数学九年级上册苏科版
参考答案与试题解析
一.选择题(共8小题)
1.(2023秋 朝阳区校级期末)下列关于x的方程中,一定是一元二次方程的为( )
A.x2+2xy+y2=0 B.x2﹣2x+3=0
C. D.ax2+bx+c=0
【解答】解:A、方程x2+2xy+y2=0含有2个未知数,不是一元二次方程,故本选项不符合题意;
B、方程x2﹣2x+3=0是一元二次方程,故本选项符合题意;
C、方程的分母含未知数,不是一元二次方程,故本选项不符合题意;
D、当a=0时,方程ax2+bx+c=0不是一元二次方程,故本选项不符合题意;
故选:B.
2.(2023秋 方城县期末)关于x的一元二次方程kx2+4x﹣2=0有实数根,则k的取值范围是( )
A.k≥﹣2 B.k>﹣2且k≠0 C.k≥﹣2且k≠0 D.k≤﹣2
【解答】解:根据题意得k≠0且Δ=42﹣4k×(﹣2)≥0,
解得k≥﹣2且k≠0.
故选:C.
3.(2024春 瑶海区期中)已知一元二次方程x2﹣x﹣2=0的一个根为m,则2023﹣m2+m的值是( )
A.2020 B.2021 C.2023 D.2025
【解答】解:∵一元二次方程x2﹣x﹣2=0的一个根为m,
∴m2﹣m﹣2=0,
∴m2﹣m=2,
∴2023﹣m2+2m=2023﹣(m2﹣m)=2023﹣2=2021.
故选:B.
4.(2024春 慈溪市期末)杭州亚运会吉祥物深受大家喜爱.某商户3月份销售吉祥物“宸宸”摆件为10万个,5月份销售11.5万个.设该摆件销售量的月平均增长率为x(x>0),则可列方程为( )
A.10(1+x)2=11.5 B.10(1+2x)=11.5
C.10x2=11.5 D.11.5(1﹣x)2=10
【解答】解:根据题意得:10(1+x)2=11.5.
故选:A.
5.(2024 大庆二模)三角形的外心是( )
A.三边上的高线的交点
B.三边中线的交点
C.三边垂直平分线的交点
D.三个内角平分线的交点
【解答】解:三角形的外心是三边垂直平分线的交点,
故选:C.
6.(2024 雁塔区校级四模)如图,四边形ABCD内接于⊙O,已知点C为的中点,若∠A=50°,则∠CBD的度数为( )
A.50° B.40° C.30° D.25°
【解答】解:∵四边形ABCD内接于⊙O,∠A=50°,
∴∠BCD=180°﹣∠A=180°﹣50°=130°,
∵点C为的中点,
∴CD=CB,
∴∠CDB=∠CBD=×(180°﹣130°)=25°,
故选:D.
7.(2024秋 鄞州区校级月考)如图,直径AB=12的半圆绕点B按顺时针方向旋转30°,此时A到了点A′的位置,则图中阴影部分的面积是( )
A.2π B.3π C.4π D.12π
【解答】解:∵直径AB=12的半圆,绕B点顺时针旋转30°,
∴S阴影=SA'B为直径的半圆+S扇形ABA'﹣SAB为直径的半圆,
又∵AB=A'B,
∴SA'B为直径的半圆=SAB为直径的半圆,
∴S阴影=S扇形ABA',
∵AB=12,∠ABA’=30°,
∴S阴影=S扇形ABA’===12π.
故答案为:D.
8.(2024 临邑县一模)如图,在矩形ABCD中,BC=8,以AB为直径作⊙O,将矩形ABCD绕点B旋转,使所得矩形A'BC'D'的边C'D'与⊙O相切,切点为E,边A'B与⊙O相交于点F.若BF=8,则CD长为( )
A.9 B.10 C.8 D.12
【解答】解:连接OE,延长EO交BF于点M,
∵C'D'与⊙O相切,
∴∠OEC′=90°,
又矩形A'BC'D'中,A'B∥C'D',
∴∠EMB=90°,
∴BM=FM,
∵矩形ABCD绕点B旋转所得矩形为A′BC′D′,
∴∠C′=∠C=90°,AB=CD,BC=BC'=8,
∴四边形EMBC'为矩形,
∴ME=8,
设OB=OE=x,则OM=8﹣x,
∵OM2+BM2=OB2,
∴(8﹣x)2+42=x2,
解得x=5,
∴AB=CD=10.
故选:B.
二.填空题(共7小题)
9.(2024 常州模拟)一元二次方程x2﹣x=0的解是 x1=0,x2=1 .
【解答】解:x2﹣x=0,
x(x﹣1)=0,
∴x=0或x﹣1=0,
∴x1=0,x2=1,
故答案为:x1=0,x2=1.
10.(2024秋 张店区校级月考)若,则的值为 4 .
【解答】解:,
,
,
∴x﹣1=0,,
∴x=1,y=﹣2,
∴.
故答案为:4.
11.(2024秋 兴宁区月考)如图,学校课外生物小组的试验园地的形状是长50米、宽30米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为800平方米.则小道的宽为多少米?若设小道的宽为x米,则根据题意,列方程为 (50﹣2x)(30﹣x)=800 .
【解答】解:由题意可得:(50﹣2x)(30﹣x)=800,
故答案为:(50﹣2x)(30﹣x)=800.
12.(2024秋 金乡县月考)对于实数a,b定义运算“※”为a※b=a+b2,例如3※2=3+22=7,则关于x的方程x※(x+1)=5的解是 x1=﹣4,x2=1 .
【解答】解:∵x※(x+1)=5,
∴x+(x+1)2=5,
∴x2+3x﹣4=0,
(x+4)(x﹣1)=0,
x+4=0或x﹣1=0,
解得x1=﹣4,x2=1,
故答案为:x1=﹣4,x2=1.
13.(2024秋 建邺区校级期中)如图,AB、BC、CD、DA都是⊙O的切线,AD=2,AB+CD=8,则BC= 6 .
【解答】解:设AB、BC、CD、DA与⊙O的切点分别为E、H、G、F,
∵AB、BC、CD、DA都是⊙O的切线,
∴AF=AE,BE=BH,CH=CG,DG=DF,
∴AD+BC=AF+DF+BH+CH=AE+BE+DG+CG=AB+CD,
∵AD=2,AB+CD=8,
∴BC=AB+CD﹣AD=8﹣2=6,
故答案为:6.
14.(2024 盐城三模)圆在中式建筑中有着广泛的应用.如图,某园林中圆弧形门洞的顶端到地面的高度为2.8m,地面入口的宽度为1m,门枕的高度为0.3m,则该圆弧所在圆的半径为 1.3 m.
【解答】解:设该门洞的半径的半径为r m,
如图,过点圆心O作OC⊥AB于点C,延长CO交圆O于点D,连接OA,
则CD=2.8﹣0.3=2.5m,AC=BC=AB=×1=0.5(m),
∴OC=(2.5﹣r)m,
在Rt△AOC中,由勾股定理得:OA2=OC2+AC2,
0.52+(2.5﹣r)2=r2,
解得:r=1.3,
即该门洞的半径为1.3m,
故答案为:1.3.
15.(2024秋 工业园区校级月考)如图,AB是⊙O的直径,∠CAB=40°,则∠B= 50° .
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠B+∠CAB=90°,
∵∠CAB=40°,
∴∠B=50°.
故答案为:50°.
三.解答题(共7小题)
16.(2024秋 龙海区校级月考)解方程:
(1)x2﹣2x+1=3;
(2)x2﹣5x+6=0.
【解答】解:(1)x2﹣2x+1=3,
(x﹣1)2=3,
,
∴;
(2)x2﹣5x+6=0,
(x﹣2)(x﹣3)=0,
∴x﹣2=0或x﹣3=0,
解得x1=2,x2=3.
17.(2024秋 通许县期中)已知关于x的方程x2﹣(m+1)x﹣1=0.
(1)求证:无论m取什么实数值,方程总有两个不相等的实数根;
(2)若该方程的两个根互为相反数,求m的值.
【解答】(1)证明:Δ=[﹣(m+1)]2﹣4×1×(﹣1)=(m+1)2+4,
∵(m+1)2+4>0,
∴无论m取什么实数值,方程总有两个不相等的实数根;
(2)解:设两根为x1,x2,
则由题意得:x1+x2=0,
∴m+1=0,
∴m=﹣1.
18.(2024秋 邗江区校级月考)烟花三月下扬州,东关街区人如流.东关街某店铺以每件45元的批发价购进一批长毛绒玩偶盲盒,以每件68元的价格出售,一经开售,深受游客喜爱.经统计,第一周该盲盒的销售量为256件,第三周的销售量达到400件.
(1)求该盲盒第一周到第三周销售量的周平均增长率;
(2)从第四周起,店铺经营者决定采用降价促销的方式回馈游客,经试验,发现该盲盒每降价1元,周销售量就会增加20件.当该盲盒售价为多少元时,周销售利润达8400元?
【解答】解:(1)设该盲盒第一周到第三周销售量的周平均增长率为x;
∴256(1+x)2=400,
∴x=0.25或x=﹣2.25(舍去),
∴周平均增长率为25%;
(2)设该盲盒售价为a元时,周销售利润达8400元,a<68,
∴,
∴a2﹣133a+4380=0,
∴(a﹣60)(a﹣73)=0,
a=60或a=73(舍去),
∴该盲盒售价为60元时,利润达8400元.
19.(2024 济南模拟)(1)尺规作图,作出△ABC的外接圆(不写作图过程,但保留作图痕迹);
(2)若AB=,∠B=45°,BC=6,求△ABC外接圆的半径长.
【解答】解:(1)尺规作图,如图1,
(2)如图所示,连接OB,
∵DH、OE分别垂直平分AB、BC,AB=,BC=6,
∴BD=,BE=3,
又∵∠ABC=45°,∠BDO=90°,
∴BH=4,∠EHO=45°,
∴OE=EH=BH﹣BE=4﹣3=1,
∴BO=,
∴△ABC外接圆的半径长.
20.(2024 烟台一模)如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.
(1)求证:BD为圆的直径;
(2)过点C作CF∥AD交AB的延长线于点F,若AC=AD,BF=2,求此圆半径的长.
【解答】(1)证明:∵∠BAC=∠ADB,
又∵∠BAC=∠CDB,
∴∠CDB=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
∴∠CDB+∠ADB+∠ABD+∠CBD=180°,
∴2(∠ADB+∠ABD)=180°,
即∠ADB+∠ABD=90°,
∴∠BAD=90°,
∴BD为圆的直径;
(2)解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴,
∴AD=CD,
∵AC=AD,
∴AC=AD=CD,
∴△ACD是等边三角形,
∴∠ADC=60°,
∴∠ABC=180°﹣∠ADC=180°﹣60°=120°,
∴∠CBF=180°﹣∠ABC=180°﹣120°=60°,
∵CF∥AD,
∴∠BAD+∠F=180°,
∵∠BAD=90°,
∴∠F=90°,
∴∠BCF=30°,
∴BC=2BF,
∵BF=2,
∴BC=4,
∵BD为直径,
∴∠BCD=90°,
∵∠ADB=∠CDB,∠ADC=60°,
∴∠CDB=30°,
∴BD=2BC=8,
∴圆的半径长为4.
21.(2023秋 武胜县期末)HUAWEIMate60Pro于8月29日上市,该系列完成了核心技术领域从0到1的跃迁,让无数国人为之自豪并被赞誉为“争气机”.手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量.圆弧对应的弦AB长80mm,弓形高CD长14mm求半径OA的长.
【解答】解:设半径OA的长为r mm,
则OA=OC=OB=r mm,
∵弓形高CD=14mm,
∴OD=(r﹣14)mm,
∵OC⊥AB,AB=80mm,
∴AD=AB=40mm,
在Rt△OAD中,由勾股定理得:OA2﹣OD2=AD2,
即r2﹣(r﹣14)2=402,
解得:r=.
答:半径OA的长为mm.
22.(2024 海陵区一模)学习下面方框内的内容,并解答下列问题:
小明在反思学习时,发现解决下列3个问题时都用到了同一种数学思想方法: 问题1:若a﹣2b=3,求2a﹣4b+1的值. 解决思路:2a﹣4b+1=2(a﹣2b)+1=2×3+1=7. 问题2:如图1,分别以△ABC的3个顶点为圆心,2为半径画圆,求图中3块阴影面积之和. 解决思路:将3块阴影扇形拼成一个半径为2的半圆,则阴影面积为2π. 问题3:已知a2+b2=3ab(a>b>0),求的值. 解题思路:对已知条件进行恒等变形,a2+b2+2ab=5ab,(a+b)2=5ab,因为a>b>0,所以,类似可以得到a﹣b=….
问题:
(1)方框内3个问题的解决都用到了 C 的数学思想方法(从下列选项中选一个);
A.分类讨论
B.数形结合
C.整体
D.从特殊到一般
(2)方框内问题3中的值为 ;
(3)如图2,已知⊙O的半径为5,AB、CD是⊙O的弦,且AB=8,CD=6,求与的长度之和.
【解答】解:(1)由题中所给三个问题可知,
在解决问题的过程中都用到了整体思想.
故选:C.
(2)继续问题3的解题过程,
a2+b2﹣2ab=ab,
所以(a﹣b)2=ab,
因为a>b>0,
所以a﹣b=,
所以=.
故答案为:.
(3)连接AO并延长,交⊙O交于点M,连接MB,
∵AM是⊙O的直径,
∴∠ABM=90°.
在Rt△ABM中,
BM=,
∴BM=CD,
∴,
∴.
又∵∠AOM=180°,
∴=,
即与的长度之和为5π.
一.选择题(共8小题)
1.(2023秋 朝阳区校级期末)下列关于x的方程中,一定是一元二次方程的为( )
A.x2+2xy+y2=0 B.x2﹣2x+3=0
C. D.ax2+bx+c=0
2.(2023秋 方城县期末)关于x的一元二次方程kx2+4x﹣2=0有实数根,则k的取值范围是( )
A.k≥﹣2 B.k>﹣2且k≠0 C.k≥﹣2且k≠0 D.k≤﹣2
3.(2024春 瑶海区期中)已知一元二次方程x2﹣x﹣2=0的一个根为m,则2023﹣m2+m的值是( )
A.2020 B.2021 C.2023 D.2025
4.(2024春 慈溪市期末)杭州亚运会吉祥物深受大家喜爱.某商户3月份销售吉祥物“宸宸”摆件为10万个,5月份销售11.5万个.设该摆件销售量的月平均增长率为x(x>0),则可列方程为( )
A.10(1+x)2=11.5 B.10(1+2x)=11.5
C.10x2=11.5 D.11.5(1﹣x)2=10
5.(2024 大庆二模)三角形的外心是( )
A.三边上的高线的交点
B.三边中线的交点
C.三边垂直平分线的交点
D.三个内角平分线的交点
6.(2024 雁塔区校级四模)如图,四边形ABCD内接于⊙O,已知点C为的中点,若∠A=50°,则∠CBD的度数为( )
A.50° B.40° C.30° D.25°
7.(2024秋 鄞州区校级月考)如图,直径AB=12的半圆绕点B按顺时针方向旋转30°,此时A到了点A′的位置,则图中阴影部分的面积是( )
A.2π B.3π C.4π D.12π
8.(2024 临邑县一模)如图,在矩形ABCD中,BC=8,以AB为直径作⊙O,将矩形ABCD绕点B旋转,使所得矩形A'BC'D'的边C'D'与⊙O相切,切点为E,边A'B与⊙O相交于点F.若BF=8,则CD长为( )
A.9 B.10 C.8 D.12
二.填空题(共7小题)
9.(2024 常州模拟)一元二次方程x2﹣x=0的解是 .
10.(2024秋 张店区校级月考)若,则的值为 .
11.(2024秋 兴宁区月考)如图,学校课外生物小组的试验园地的形状是长50米、宽30米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为800平方米.则小道的宽为多少米?若设小道的宽为x米,则根据题意,列方程为 .
12.(2024秋 金乡县月考)对于实数a,b定义运算“※”为a※b=a+b2,例如3※2=3+22=7,则关于x的方程x※(x+1)=5的解是 .
13.(2024秋 建邺区校级期中)如图,AB、BC、CD、DA都是⊙O的切线,AD=2,AB+CD=8,则BC= .
14.(2024 盐城三模)圆在中式建筑中有着广泛的应用.如图,某园林中圆弧形门洞的顶端到地面的高度为2.8m,地面入口的宽度为1m,门枕的高度为0.3m,则该圆弧所在圆的半径为 m.
15.(2024秋 工业园区校级月考)如图,AB是⊙O的直径,∠CAB=40°,则∠B= .
三.解答题(共7小题)
16.(2024秋 龙海区校级月考)解方程:
(1)x2﹣2x+1=3;
(2)x2﹣5x+6=0.
17.(2024秋 通许县期中)已知关于x的方程x2﹣(m+1)x﹣1=0.
(1)求证:无论m取什么实数值,方程总有两个不相等的实数根;
(2)若该方程的两个根互为相反数,求m的值.
18.(2024秋 邗江区校级月考)烟花三月下扬州,东关街区人如流.东关街某店铺以每件45元的批发价购进一批长毛绒玩偶盲盒,以每件68元的价格出售,一经开售,深受游客喜爱.经统计,第一周该盲盒的销售量为256件,第三周的销售量达到400件.
(1)求该盲盒第一周到第三周销售量的周平均增长率;
(2)从第四周起,店铺经营者决定采用降价促销的方式回馈游客,经试验,发现该盲盒每降价1元,周销售量就会增加20件.当该盲盒售价为多少元时,周销售利润达8400元?
19.(2024 济南模拟)(1)尺规作图,作出△ABC的外接圆(不写作图过程,但保留作图痕迹);
(2)若AB=,∠B=45°,BC=6,求△ABC外接圆的半径长.
20.(2024 烟台一模)如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.
(1)求证:BD为圆的直径;
(2)过点C作CF∥AD交AB的延长线于点F,若AC=AD,BF=2,求此圆半径的长.
21.(2023秋 武胜县期末)HUAWEIMate60Pro于8月29日上市,该系列完成了核心技术领域从0到1的跃迁,让无数国人为之自豪并被赞誉为“争气机”.手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量.圆弧对应的弦AB长80mm,弓形高CD长14mm求半径OA的长.
22.(2024 海陵区一模)学习下面方框内的内容,并解答下列问题:
小明在反思学习时,发现解决下列3个问题时都用到了同一种数学思想方法: 问题1:若a﹣2b=3,求2a﹣4b+1的值. 解决思路:2a﹣4b+1=2(a﹣2b)+1=2×3+1=7. 问题2:如图1,分别以△ABC的3个顶点为圆心,2为半径画圆,求图中3块阴影面积之和. 解决思路:将3块阴影扇形拼成一个半径为2的半圆,则阴影面积为2π. 问题3:已知a2+b2=3ab(a>b>0),求的值. 解题思路:对已知条件进行恒等变形,a2+b2+2ab=5ab,(a+b)2=5ab,因为a>b>0,所以,类似可以得到a﹣b=….
问题:
(1)方框内3个问题的解决都用到了 的数学思想方法(从下列选项中选一个);
A.分类讨论
B.数形结合
C.整体
D.从特殊到一般
(2)方框内问题3中的值为 ;
(3)如图2,已知⊙O的半径为5,AB、CD是⊙O的弦,且AB=8,CD=6,求与的长度之和.
第1-2章阶段检测卷-2024-2025学年数学九年级上册苏科版
参考答案与试题解析
一.选择题(共8小题)
1.(2023秋 朝阳区校级期末)下列关于x的方程中,一定是一元二次方程的为( )
A.x2+2xy+y2=0 B.x2﹣2x+3=0
C. D.ax2+bx+c=0
【解答】解:A、方程x2+2xy+y2=0含有2个未知数,不是一元二次方程,故本选项不符合题意;
B、方程x2﹣2x+3=0是一元二次方程,故本选项符合题意;
C、方程的分母含未知数,不是一元二次方程,故本选项不符合题意;
D、当a=0时,方程ax2+bx+c=0不是一元二次方程,故本选项不符合题意;
故选:B.
2.(2023秋 方城县期末)关于x的一元二次方程kx2+4x﹣2=0有实数根,则k的取值范围是( )
A.k≥﹣2 B.k>﹣2且k≠0 C.k≥﹣2且k≠0 D.k≤﹣2
【解答】解:根据题意得k≠0且Δ=42﹣4k×(﹣2)≥0,
解得k≥﹣2且k≠0.
故选:C.
3.(2024春 瑶海区期中)已知一元二次方程x2﹣x﹣2=0的一个根为m,则2023﹣m2+m的值是( )
A.2020 B.2021 C.2023 D.2025
【解答】解:∵一元二次方程x2﹣x﹣2=0的一个根为m,
∴m2﹣m﹣2=0,
∴m2﹣m=2,
∴2023﹣m2+2m=2023﹣(m2﹣m)=2023﹣2=2021.
故选:B.
4.(2024春 慈溪市期末)杭州亚运会吉祥物深受大家喜爱.某商户3月份销售吉祥物“宸宸”摆件为10万个,5月份销售11.5万个.设该摆件销售量的月平均增长率为x(x>0),则可列方程为( )
A.10(1+x)2=11.5 B.10(1+2x)=11.5
C.10x2=11.5 D.11.5(1﹣x)2=10
【解答】解:根据题意得:10(1+x)2=11.5.
故选:A.
5.(2024 大庆二模)三角形的外心是( )
A.三边上的高线的交点
B.三边中线的交点
C.三边垂直平分线的交点
D.三个内角平分线的交点
【解答】解:三角形的外心是三边垂直平分线的交点,
故选:C.
6.(2024 雁塔区校级四模)如图,四边形ABCD内接于⊙O,已知点C为的中点,若∠A=50°,则∠CBD的度数为( )
A.50° B.40° C.30° D.25°
【解答】解:∵四边形ABCD内接于⊙O,∠A=50°,
∴∠BCD=180°﹣∠A=180°﹣50°=130°,
∵点C为的中点,
∴CD=CB,
∴∠CDB=∠CBD=×(180°﹣130°)=25°,
故选:D.
7.(2024秋 鄞州区校级月考)如图,直径AB=12的半圆绕点B按顺时针方向旋转30°,此时A到了点A′的位置,则图中阴影部分的面积是( )
A.2π B.3π C.4π D.12π
【解答】解:∵直径AB=12的半圆,绕B点顺时针旋转30°,
∴S阴影=SA'B为直径的半圆+S扇形ABA'﹣SAB为直径的半圆,
又∵AB=A'B,
∴SA'B为直径的半圆=SAB为直径的半圆,
∴S阴影=S扇形ABA',
∵AB=12,∠ABA’=30°,
∴S阴影=S扇形ABA’===12π.
故答案为:D.
8.(2024 临邑县一模)如图,在矩形ABCD中,BC=8,以AB为直径作⊙O,将矩形ABCD绕点B旋转,使所得矩形A'BC'D'的边C'D'与⊙O相切,切点为E,边A'B与⊙O相交于点F.若BF=8,则CD长为( )
A.9 B.10 C.8 D.12
【解答】解:连接OE,延长EO交BF于点M,
∵C'D'与⊙O相切,
∴∠OEC′=90°,
又矩形A'BC'D'中,A'B∥C'D',
∴∠EMB=90°,
∴BM=FM,
∵矩形ABCD绕点B旋转所得矩形为A′BC′D′,
∴∠C′=∠C=90°,AB=CD,BC=BC'=8,
∴四边形EMBC'为矩形,
∴ME=8,
设OB=OE=x,则OM=8﹣x,
∵OM2+BM2=OB2,
∴(8﹣x)2+42=x2,
解得x=5,
∴AB=CD=10.
故选:B.
二.填空题(共7小题)
9.(2024 常州模拟)一元二次方程x2﹣x=0的解是 x1=0,x2=1 .
【解答】解:x2﹣x=0,
x(x﹣1)=0,
∴x=0或x﹣1=0,
∴x1=0,x2=1,
故答案为:x1=0,x2=1.
10.(2024秋 张店区校级月考)若,则的值为 4 .
【解答】解:,
,
,
∴x﹣1=0,,
∴x=1,y=﹣2,
∴.
故答案为:4.
11.(2024秋 兴宁区月考)如图,学校课外生物小组的试验园地的形状是长50米、宽30米的矩形,为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为800平方米.则小道的宽为多少米?若设小道的宽为x米,则根据题意,列方程为 (50﹣2x)(30﹣x)=800 .
【解答】解:由题意可得:(50﹣2x)(30﹣x)=800,
故答案为:(50﹣2x)(30﹣x)=800.
12.(2024秋 金乡县月考)对于实数a,b定义运算“※”为a※b=a+b2,例如3※2=3+22=7,则关于x的方程x※(x+1)=5的解是 x1=﹣4,x2=1 .
【解答】解:∵x※(x+1)=5,
∴x+(x+1)2=5,
∴x2+3x﹣4=0,
(x+4)(x﹣1)=0,
x+4=0或x﹣1=0,
解得x1=﹣4,x2=1,
故答案为:x1=﹣4,x2=1.
13.(2024秋 建邺区校级期中)如图,AB、BC、CD、DA都是⊙O的切线,AD=2,AB+CD=8,则BC= 6 .
【解答】解:设AB、BC、CD、DA与⊙O的切点分别为E、H、G、F,
∵AB、BC、CD、DA都是⊙O的切线,
∴AF=AE,BE=BH,CH=CG,DG=DF,
∴AD+BC=AF+DF+BH+CH=AE+BE+DG+CG=AB+CD,
∵AD=2,AB+CD=8,
∴BC=AB+CD﹣AD=8﹣2=6,
故答案为:6.
14.(2024 盐城三模)圆在中式建筑中有着广泛的应用.如图,某园林中圆弧形门洞的顶端到地面的高度为2.8m,地面入口的宽度为1m,门枕的高度为0.3m,则该圆弧所在圆的半径为 1.3 m.
【解答】解:设该门洞的半径的半径为r m,
如图,过点圆心O作OC⊥AB于点C,延长CO交圆O于点D,连接OA,
则CD=2.8﹣0.3=2.5m,AC=BC=AB=×1=0.5(m),
∴OC=(2.5﹣r)m,
在Rt△AOC中,由勾股定理得:OA2=OC2+AC2,
0.52+(2.5﹣r)2=r2,
解得:r=1.3,
即该门洞的半径为1.3m,
故答案为:1.3.
15.(2024秋 工业园区校级月考)如图,AB是⊙O的直径,∠CAB=40°,则∠B= 50° .
【解答】解:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠B+∠CAB=90°,
∵∠CAB=40°,
∴∠B=50°.
故答案为:50°.
三.解答题(共7小题)
16.(2024秋 龙海区校级月考)解方程:
(1)x2﹣2x+1=3;
(2)x2﹣5x+6=0.
【解答】解:(1)x2﹣2x+1=3,
(x﹣1)2=3,
,
∴;
(2)x2﹣5x+6=0,
(x﹣2)(x﹣3)=0,
∴x﹣2=0或x﹣3=0,
解得x1=2,x2=3.
17.(2024秋 通许县期中)已知关于x的方程x2﹣(m+1)x﹣1=0.
(1)求证:无论m取什么实数值,方程总有两个不相等的实数根;
(2)若该方程的两个根互为相反数,求m的值.
【解答】(1)证明:Δ=[﹣(m+1)]2﹣4×1×(﹣1)=(m+1)2+4,
∵(m+1)2+4>0,
∴无论m取什么实数值,方程总有两个不相等的实数根;
(2)解:设两根为x1,x2,
则由题意得:x1+x2=0,
∴m+1=0,
∴m=﹣1.
18.(2024秋 邗江区校级月考)烟花三月下扬州,东关街区人如流.东关街某店铺以每件45元的批发价购进一批长毛绒玩偶盲盒,以每件68元的价格出售,一经开售,深受游客喜爱.经统计,第一周该盲盒的销售量为256件,第三周的销售量达到400件.
(1)求该盲盒第一周到第三周销售量的周平均增长率;
(2)从第四周起,店铺经营者决定采用降价促销的方式回馈游客,经试验,发现该盲盒每降价1元,周销售量就会增加20件.当该盲盒售价为多少元时,周销售利润达8400元?
【解答】解:(1)设该盲盒第一周到第三周销售量的周平均增长率为x;
∴256(1+x)2=400,
∴x=0.25或x=﹣2.25(舍去),
∴周平均增长率为25%;
(2)设该盲盒售价为a元时,周销售利润达8400元,a<68,
∴,
∴a2﹣133a+4380=0,
∴(a﹣60)(a﹣73)=0,
a=60或a=73(舍去),
∴该盲盒售价为60元时,利润达8400元.
19.(2024 济南模拟)(1)尺规作图,作出△ABC的外接圆(不写作图过程,但保留作图痕迹);
(2)若AB=,∠B=45°,BC=6,求△ABC外接圆的半径长.
【解答】解:(1)尺规作图,如图1,
(2)如图所示,连接OB,
∵DH、OE分别垂直平分AB、BC,AB=,BC=6,
∴BD=,BE=3,
又∵∠ABC=45°,∠BDO=90°,
∴BH=4,∠EHO=45°,
∴OE=EH=BH﹣BE=4﹣3=1,
∴BO=,
∴△ABC外接圆的半径长.
20.(2024 烟台一模)如图,圆内接四边形ABCD的对角线AC,BD交于点E,BD平分∠ABC,∠BAC=∠ADB.
(1)求证:BD为圆的直径;
(2)过点C作CF∥AD交AB的延长线于点F,若AC=AD,BF=2,求此圆半径的长.
【解答】(1)证明:∵∠BAC=∠ADB,
又∵∠BAC=∠CDB,
∴∠CDB=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵四边形ABCD是圆内接四边形,
∴∠ABC+∠ADC=180°,
∴∠CDB+∠ADB+∠ABD+∠CBD=180°,
∴2(∠ADB+∠ABD)=180°,
即∠ADB+∠ABD=90°,
∴∠BAD=90°,
∴BD为圆的直径;
(2)解:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴,
∴AD=CD,
∵AC=AD,
∴AC=AD=CD,
∴△ACD是等边三角形,
∴∠ADC=60°,
∴∠ABC=180°﹣∠ADC=180°﹣60°=120°,
∴∠CBF=180°﹣∠ABC=180°﹣120°=60°,
∵CF∥AD,
∴∠BAD+∠F=180°,
∵∠BAD=90°,
∴∠F=90°,
∴∠BCF=30°,
∴BC=2BF,
∵BF=2,
∴BC=4,
∵BD为直径,
∴∠BCD=90°,
∵∠ADB=∠CDB,∠ADC=60°,
∴∠CDB=30°,
∴BD=2BC=8,
∴圆的半径长为4.
21.(2023秋 武胜县期末)HUAWEIMate60Pro于8月29日上市,该系列完成了核心技术领域从0到1的跃迁,让无数国人为之自豪并被赞誉为“争气机”.手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量.圆弧对应的弦AB长80mm,弓形高CD长14mm求半径OA的长.
【解答】解:设半径OA的长为r mm,
则OA=OC=OB=r mm,
∵弓形高CD=14mm,
∴OD=(r﹣14)mm,
∵OC⊥AB,AB=80mm,
∴AD=AB=40mm,
在Rt△OAD中,由勾股定理得:OA2﹣OD2=AD2,
即r2﹣(r﹣14)2=402,
解得:r=.
答:半径OA的长为mm.
22.(2024 海陵区一模)学习下面方框内的内容,并解答下列问题:
小明在反思学习时,发现解决下列3个问题时都用到了同一种数学思想方法: 问题1:若a﹣2b=3,求2a﹣4b+1的值. 解决思路:2a﹣4b+1=2(a﹣2b)+1=2×3+1=7. 问题2:如图1,分别以△ABC的3个顶点为圆心,2为半径画圆,求图中3块阴影面积之和. 解决思路:将3块阴影扇形拼成一个半径为2的半圆,则阴影面积为2π. 问题3:已知a2+b2=3ab(a>b>0),求的值. 解题思路:对已知条件进行恒等变形,a2+b2+2ab=5ab,(a+b)2=5ab,因为a>b>0,所以,类似可以得到a﹣b=….
问题:
(1)方框内3个问题的解决都用到了 C 的数学思想方法(从下列选项中选一个);
A.分类讨论
B.数形结合
C.整体
D.从特殊到一般
(2)方框内问题3中的值为 ;
(3)如图2,已知⊙O的半径为5,AB、CD是⊙O的弦,且AB=8,CD=6,求与的长度之和.
【解答】解:(1)由题中所给三个问题可知,
在解决问题的过程中都用到了整体思想.
故选:C.
(2)继续问题3的解题过程,
a2+b2﹣2ab=ab,
所以(a﹣b)2=ab,
因为a>b>0,
所以a﹣b=,
所以=.
故答案为:.
(3)连接AO并延长,交⊙O交于点M,连接MB,
∵AM是⊙O的直径,
∴∠ABM=90°.
在Rt△ABM中,
BM=,
∴BM=CD,
∴,
∴.
又∵∠AOM=180°,
∴=,
即与的长度之和为5π.
同课章节目录
