2024-2025学年甘肃省兰州五十九中高三(上)月考数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年甘肃省兰州五十九中高三(上)月考数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 91.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-02 13:36:24 | ||
图片预览




文档简介
2024-2025学年甘肃省兰州五十九中高三(上)月考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.复数满足,则( )
A. B. C. D.
2.已知所在平面内一点,满足,则( )
A. B. C. D.
3.( )
A. B. C. D.
4.已知符号函数则函数的图象大致为( )
A. B.
C. D.
5.已知直线与曲线相切,则的方程不可能是( )
A. B. C. D.
6.为迎接元宵节,某广场将一个圆形区域分成,,,,五个部分如图所示,现用种颜色的鲜花进行装扮种颜色均用到,每部分用一种颜色,相邻部分用不同颜色,则该区域鲜花的摆放方案共有( )
A. 种
B. 种
C. 种
D. 种
7.直线:与直线:相交于点,则的取值范围是( )
A. B.
C. D.
8.设方程的两根为,,则( )
A. , B.
C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.设,是两条不同的直线,,是两个不同的平面,则下列命题正确的有( )
A. 若,,则 B. 若,,则
C. 若,,,则 D. 若,,,则
10.已知第一组样本数据,,,的极差为,中位数为,平均数为,标准差为;第二组样本数据,,,的极差为,中位数为,平均数为,标准差为若满足,则( )
A. B. C. D.
11.抛物线:的焦点为,、是抛物线上的两个动点,是线段的中点,过作准线的垂线,垂足为,则( )
A. 若,则直线的斜率为或
B. 若,则
C. 若和不平行,则
D. 若,则的最大值为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知圆锥的高为,其顶点和底面圆周都在直径为的球面上,则圆锥的体积为______.
13.已知向量不共线,,若,则 ______.
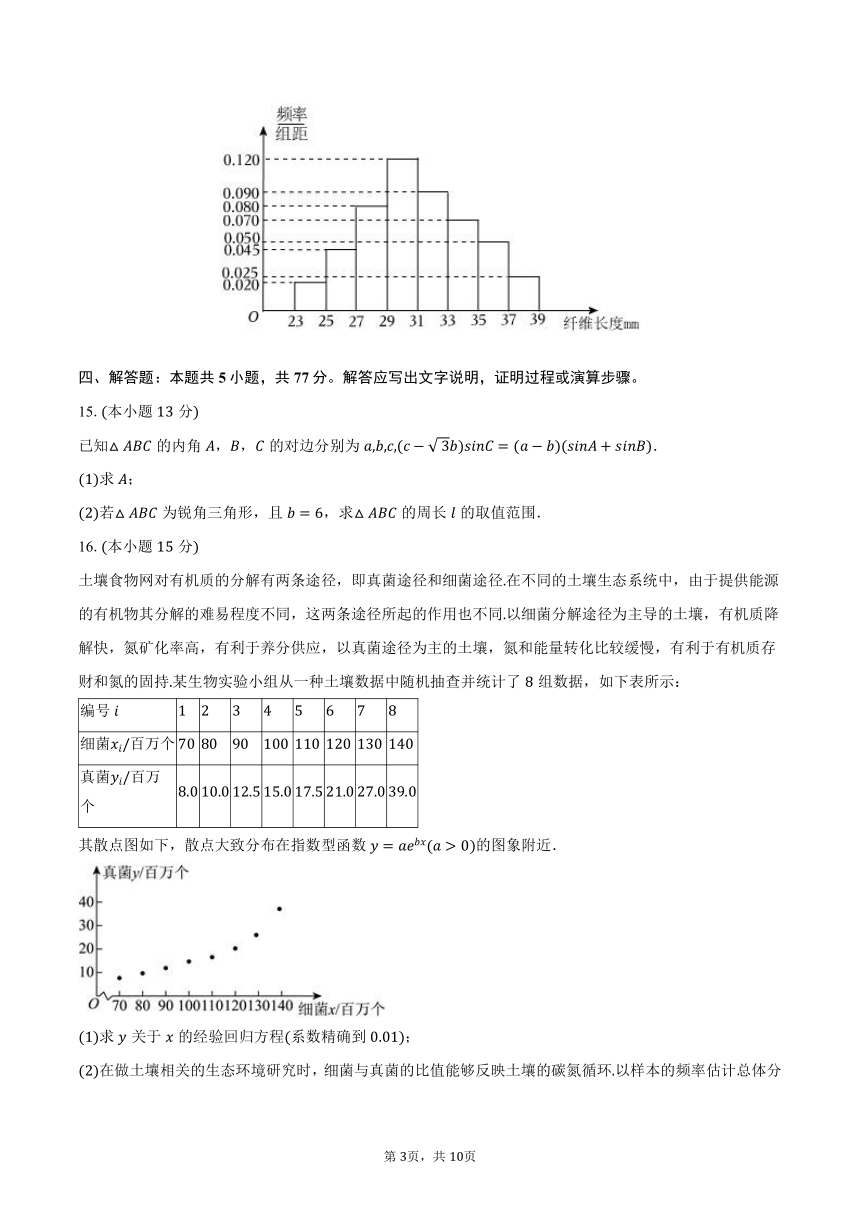
14.某厂家为了保证防寒服的质量,从生产的保暖絮片中随机抽取多组,得到每组纤维长度单位:的均值,并制成如下所示的频率分布直方图,由此估计其纤维长度均值的分位数是______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知的内角,,的对边分别为.
求;
若为锐角三角形,且,求的周长的取值范围.
16.本小题分
土壤食物网对有机质的分解有两条途径,即真菌途径和细菌途径在不同的土壤生态系统中,由于提供能源的有机物其分解的难易程度不同,这两条途径所起的作用也不同以细菌分解途径为主导的土壤,有机质降解快,氮矿化率高,有利于养分供应,以真菌途径为主的土壤,氮和能量转化比较缓慢,有利于有机质存财和氮的固持某生物实验小组从一种土壤数据中随机抽查并统计了组数据,如下表所示:
编号
细菌百万个
真菌百万个
其散点图如下,散点大致分布在指数型函数的图象附近.
求关于的经验回归方程系数精确到;
在做土壤相关的生态环境研究时,细菌与真菌的比值能够反映土壤的碳氮循环以样本的频率估计总体分布的概率,若该实验小组随机抽查组数据,再从中任选组,记真菌单位:百万个与细菌单位:百万个的数值之比位于区间内的组数为,求的分布列与数学期望.
附:经验回归方程的斜率和截距的最小二乘估计公式分别为,,
.
17.本小题分
如图,在矩形纸片中,,,沿将折起,使点到达点的位置,点在平面的射影落在边上.
求的长度;
若是边上的一个动点,是否存在点,使得平面与平面的夹角余弦值为?若存在,求的长度;若不存在,说明理由.
18.本小题分
已知、是双曲线的左、右焦点,直线经过双曲线的左焦点,与双曲线左、右两支分别相交于、两点.
求直线斜率的取值范围;
若,求的面积.
19.本小题分
已知函数.
若函数有两个零点,求实数的取值范围;
已知,,其中且,,成等比数列是曲线上三个不同的点,判断直线与曲线在点处的切线能否平行?请说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:因为,
可得,
可得,
故,
而,
所以;
由知,
而,
故由正弦定理得,
则,
可得,
由为锐角三角形,
则,
则,
故的周长
,
而,
故,
故的周长的取值范围为.
16.解:由于,故,,
令,,
则,,
所以,
所以,
故,
则关于的经验回归方程为;
由已知图表可知从第组到第组的真菌单位:百万个与细菌单位:百万个的数值之比依次为:
,,,,,,,
,
故样本中比值位于内的组数有组,
则的可能取值为:,,,,,
则,,,,,
故的分布列为:
则.
17.解:作,垂足为,连接,如图所示:
由点在平面的射影落在边上可得平面,
又平面,所以,
因为,且,平面,
所以平面,
又平面,所以,
又因为为矩形,,可得,
由,可得,
所以,;
由可得,即;
即的长度为.
根据题意,以点为坐标原点,以过点且平行于的直线为轴,分别以,所在直线为,轴建立空间直角坐标系,如图所示:
则,
所以,设,
则,所以;
易知,,
设平面的一个法向量为,则,,
所以,
解得,取,则,所以,
设平面的一个法向量为,则,,
所以,
解得,取,则,所以,
因此可得,整理可得,
解得舍或;
因此,即可得.
所以的长度为.
18.解:在双曲线中,,,则,
该双曲线的左焦点为,若直线的斜率不存在,则直线与双曲线交于左支上的两点,不合乎题意,
设直线的方程为,设点、,
联立可得,
因为直线与双曲线左、右两支分别相交于、两点,
所以,,解得,
因此,直线的斜率的取值范围是.
因为,,
由可得,则,
当直线与轴重合时,则点、,,,
此时,,不合乎题意,
设直线的方程为,联立可得,
由可得,则或,
由韦达定理可得,则,
,即,解得,则,
所以,.
19.解:令,由题设知方程有两个实数根,
因为,
当时,,单调递减,当时,,单调递增,
当时,函数取得极小值,
当及时,,且,
当时,且时.
所以当时,与有两个不同的交点,即有两个不同的零点.
因为且,,成等比数列,设公比为,
则,,分
直线的斜率,
函数在点处的切线斜率,
假设直线与函数在点处的切线平行,则,
整理成,
令,,则,
所以在单调递增,所以,
所以在时无实数解,
所以直线与函数在点处的切线不能平行.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.复数满足,则( )
A. B. C. D.
2.已知所在平面内一点,满足,则( )
A. B. C. D.
3.( )
A. B. C. D.
4.已知符号函数则函数的图象大致为( )
A. B.
C. D.
5.已知直线与曲线相切,则的方程不可能是( )
A. B. C. D.
6.为迎接元宵节,某广场将一个圆形区域分成,,,,五个部分如图所示,现用种颜色的鲜花进行装扮种颜色均用到,每部分用一种颜色,相邻部分用不同颜色,则该区域鲜花的摆放方案共有( )
A. 种
B. 种
C. 种
D. 种
7.直线:与直线:相交于点,则的取值范围是( )
A. B.
C. D.
8.设方程的两根为,,则( )
A. , B.
C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.设,是两条不同的直线,,是两个不同的平面,则下列命题正确的有( )
A. 若,,则 B. 若,,则
C. 若,,,则 D. 若,,,则
10.已知第一组样本数据,,,的极差为,中位数为,平均数为,标准差为;第二组样本数据,,,的极差为,中位数为,平均数为,标准差为若满足,则( )
A. B. C. D.
11.抛物线:的焦点为,、是抛物线上的两个动点,是线段的中点,过作准线的垂线,垂足为,则( )
A. 若,则直线的斜率为或
B. 若,则
C. 若和不平行,则
D. 若,则的最大值为
三、填空题:本题共3小题,每小题5分,共15分。
12.已知圆锥的高为,其顶点和底面圆周都在直径为的球面上,则圆锥的体积为______.
13.已知向量不共线,,若,则 ______.
14.某厂家为了保证防寒服的质量,从生产的保暖絮片中随机抽取多组,得到每组纤维长度单位:的均值,并制成如下所示的频率分布直方图,由此估计其纤维长度均值的分位数是______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知的内角,,的对边分别为.
求;
若为锐角三角形,且,求的周长的取值范围.
16.本小题分
土壤食物网对有机质的分解有两条途径,即真菌途径和细菌途径在不同的土壤生态系统中,由于提供能源的有机物其分解的难易程度不同,这两条途径所起的作用也不同以细菌分解途径为主导的土壤,有机质降解快,氮矿化率高,有利于养分供应,以真菌途径为主的土壤,氮和能量转化比较缓慢,有利于有机质存财和氮的固持某生物实验小组从一种土壤数据中随机抽查并统计了组数据,如下表所示:
编号
细菌百万个
真菌百万个
其散点图如下,散点大致分布在指数型函数的图象附近.
求关于的经验回归方程系数精确到;
在做土壤相关的生态环境研究时,细菌与真菌的比值能够反映土壤的碳氮循环以样本的频率估计总体分布的概率,若该实验小组随机抽查组数据,再从中任选组,记真菌单位:百万个与细菌单位:百万个的数值之比位于区间内的组数为,求的分布列与数学期望.
附:经验回归方程的斜率和截距的最小二乘估计公式分别为,,
.
17.本小题分
如图,在矩形纸片中,,,沿将折起,使点到达点的位置,点在平面的射影落在边上.
求的长度;
若是边上的一个动点,是否存在点,使得平面与平面的夹角余弦值为?若存在,求的长度;若不存在,说明理由.
18.本小题分
已知、是双曲线的左、右焦点,直线经过双曲线的左焦点,与双曲线左、右两支分别相交于、两点.
求直线斜率的取值范围;
若,求的面积.
19.本小题分
已知函数.
若函数有两个零点,求实数的取值范围;
已知,,其中且,,成等比数列是曲线上三个不同的点,判断直线与曲线在点处的切线能否平行?请说明理由.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:因为,
可得,
可得,
故,
而,
所以;
由知,
而,
故由正弦定理得,
则,
可得,
由为锐角三角形,
则,
则,
故的周长
,
而,
故,
故的周长的取值范围为.
16.解:由于,故,,
令,,
则,,
所以,
所以,
故,
则关于的经验回归方程为;
由已知图表可知从第组到第组的真菌单位:百万个与细菌单位:百万个的数值之比依次为:
,,,,,,,
,
故样本中比值位于内的组数有组,
则的可能取值为:,,,,,
则,,,,,
故的分布列为:
则.
17.解:作,垂足为,连接,如图所示:
由点在平面的射影落在边上可得平面,
又平面,所以,
因为,且,平面,
所以平面,
又平面,所以,
又因为为矩形,,可得,
由,可得,
所以,;
由可得,即;
即的长度为.
根据题意,以点为坐标原点,以过点且平行于的直线为轴,分别以,所在直线为,轴建立空间直角坐标系,如图所示:
则,
所以,设,
则,所以;
易知,,
设平面的一个法向量为,则,,
所以,
解得,取,则,所以,
设平面的一个法向量为,则,,
所以,
解得,取,则,所以,
因此可得,整理可得,
解得舍或;
因此,即可得.
所以的长度为.
18.解:在双曲线中,,,则,
该双曲线的左焦点为,若直线的斜率不存在,则直线与双曲线交于左支上的两点,不合乎题意,
设直线的方程为,设点、,
联立可得,
因为直线与双曲线左、右两支分别相交于、两点,
所以,,解得,
因此,直线的斜率的取值范围是.
因为,,
由可得,则,
当直线与轴重合时,则点、,,,
此时,,不合乎题意,
设直线的方程为,联立可得,
由可得,则或,
由韦达定理可得,则,
,即,解得,则,
所以,.
19.解:令,由题设知方程有两个实数根,
因为,
当时,,单调递减,当时,,单调递增,
当时,函数取得极小值,
当及时,,且,
当时,且时.
所以当时,与有两个不同的交点,即有两个不同的零点.
因为且,,成等比数列,设公比为,
则,,分
直线的斜率,
函数在点处的切线斜率,
假设直线与函数在点处的切线平行,则,
整理成,
令,,则,
所以在单调递增,所以,
所以在时无实数解,
所以直线与函数在点处的切线不能平行.
第1页,共1页
同课章节目录
