第1-3章 阶段检测卷(含答案) 2024-2025学年北师大版数学八年级上册
文档属性
| 名称 | 第1-3章 阶段检测卷(含答案) 2024-2025学年北师大版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 392.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-02 18:03:50 | ||
图片预览




文档简介
第1-3章阶段检测卷-2024-2025学年数学八年级上册北师大版
一.选择题(共8小题)
1.(2024秋 工业园区校级月考)下列各组数中,不能构成直角三角形三边的是( )
A.3,4,5 B.6,8,10 C.7,24,25 D.8,12,15
2.(2024秋 工业园区校级月考)在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB边的最小距离是( )
A. B. C. D.2.5
3.(2024秋 滕州市月考)如果的平方根是±3,则x的值是( )
A.9 B.﹣9 C.81 D.﹣81
4.(2024春 禹城市校级月考)已知,,则( )
A.14.35 B.143.5 C.45.39 D.453.9
5.(2023秋 辽阳期末)如图,点A,C都是数轴上的点,AB=AC,则数轴上点C所表示的数为( )
A. B. C. D.
6.(2024秋 高新区月考)象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益部游戏.如图是一局象棋残局,已知表示棋子“马”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为( )
A.(2,3) B.(2,1) C.(1,2) D.(1,3)
7.(2024 绵阳)蝴蝶颜色炫丽,翩翩起舞时非常美丽,深受人们喜爱,它的图案具有对称美,如图,蝴蝶图案关于y轴对称,点M的对应点为M1,若点M的坐标为(﹣2,﹣3),则点M1的坐标为( )
A.(2,﹣3) B.(﹣3,2) C.(﹣2,3) D.(2,3)
8.(2024秋 柴桑区月考)如图,这是由3个正方形和2个等腰直角三角形组成的图形.若正方形A的面积为24,则正方形B的面积为( )
A.4 B.6 C.8 D.12
二.填空题(共8小题)
9.(2024秋 临汾月考)请写出一个大于3小于4的最简二次根式 .
10.(2024秋 姑苏区校级月考)某正数的平方根分别是2a+1和a+5,则a= .
11.(2024秋 永修县校级月考)用“*”表示一种新运算:对于任意正实数a,b,都有,例如,那么5*169= .
12.(2024秋 禅城区校级月考)点M在第四象限,点M到x轴的距离为3,到y轴的距离为4,则M点坐标是 .
13.(2024秋 甘井子区校级月考)如图,点A、B分别在x轴、y轴上,OA=OB,分别以点A、B为圆心,以大于长为半径画弧,两弧交于点P.若点P的坐标为(2a,3a﹣4),则a的值为 .
14.(2024秋 禅城区校级月考)如图,动点P从点A出发,沿着圆柱的侧面移动到BC的中点S,若BC=8,点P移动的最短距离为5,则圆柱的底面周长为 .
15.(2024秋 乌拉特前旗校级月考)如图,在△ABC中,AD既是△ABC的高,也是△ABC的中线,且AD=4,AC=5,BD=3,若点P在边AC上移动,则BP的最小值是 .
16.(2024春 白云区期末)如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒,当△ABP为等腰三角形时,t的取值为 .
三.解答题(共7小题)
17.(2024秋 郸城县月考)计算:.
18.(2024秋 永修县校级月考)已知:2x﹣1和4x+3是m的两个不同的平方根
(1)求x,m的值.
(2)求1﹣9x的平方根.
19.(2024秋 雁塔区校级月考)材料:2.5的整数部分是2,小数部分是0.5,小数部分可以看成是2.5﹣2得来的,类比来看,是无理数,而,所以的整数部分是1,于是可用来表示的小数部分.
根据以上材料,完成下列问题:
(1)的整数部分是 ,小数部分是 ;
(2)也是夹在相邻两个整数之间的,可以表示为,求a+b的平方根.
20.(2024秋 天长市月考)在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2),若x2﹣x1=y2﹣y1≠0,则称点A与点B互为“对角点”.例如:A(﹣1,3),B(2,6),因为2﹣(﹣1)=6﹣3≠0,所以点A与点B互为“对角点”.
(1)若点A的坐标是(4,﹣2),分别判断点B1(2,0),B2(﹣1,﹣7),B3(0,﹣6)是否为点A的“对角点”,并说明理由;
(2)若点A的坐标是(﹣2,4),其“对角点”B在坐标轴上,求点B的坐标.
21.(2024春 民勤县期末)如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足.
(1)填空:a= ,b= ;
(2)若在第三象限内有一点M(﹣2,m),用含m的式子表示△ABM的面积;
(3)在(2)条件下,线段BM与y轴相交于C(0,﹣),当时,点P是y轴上的动点,当满足△PBM的面积是△ABM的面积的2倍时,求点P的坐标.
22.(2024秋 芗城区校级月考)某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,已知∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m.
(1)△ABC是直角三角形吗,为什么?
(2)若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
23.(2024春 长清区期中)(1)计算:(2a+b)(a+b)= ;
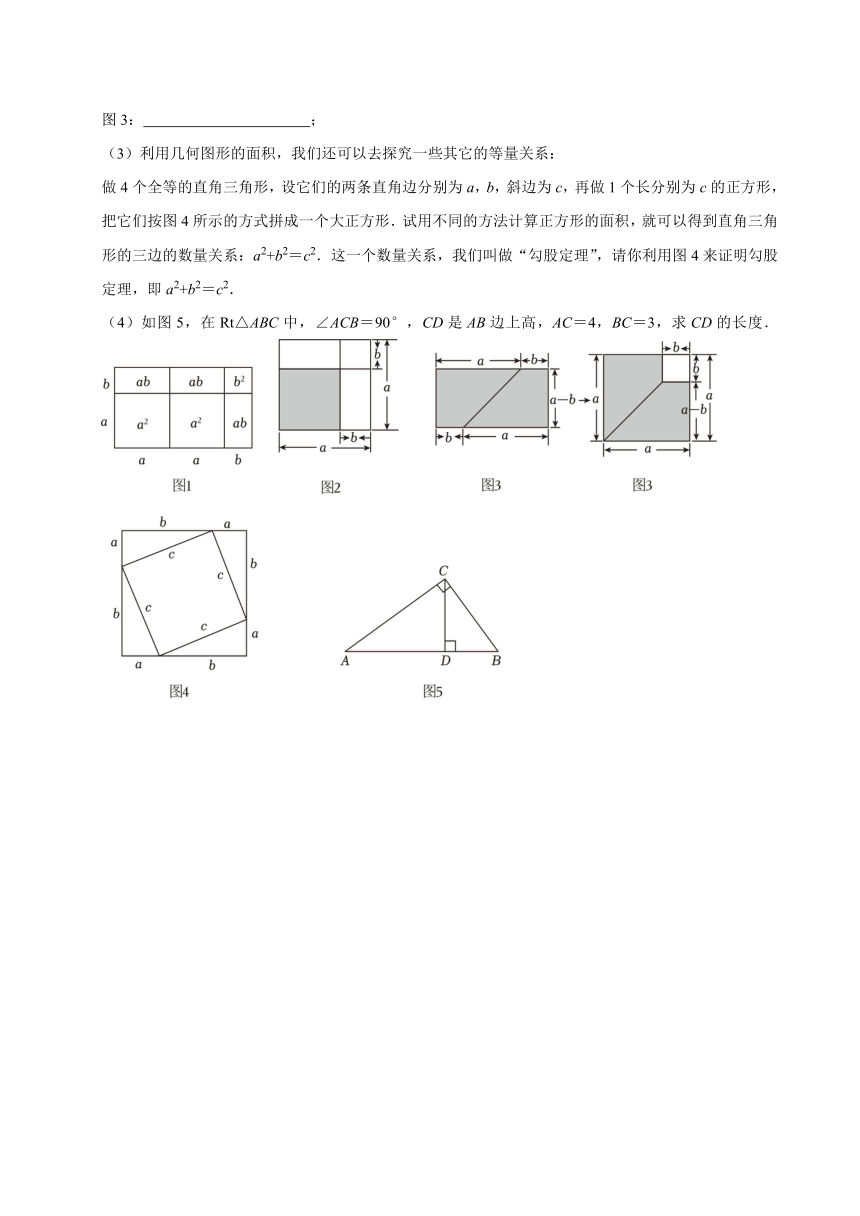
(2)图形是一种重要的数学语言,它直观形象,我们可以用几何图形的面积来解释一些代数中的等量关系.例如:上面的计算是否正确我们可以通过图1来进行验证和解释.请同学们分别写出图2、图3能解释的乘法公式:
图2: ;
图3: ;
(3)利用几何图形的面积,我们还可以去探究一些其它的等量关系:
做4个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,再做1个长分别为c的正方形,把它们按图4所示的方式拼成一个大正方形.试用不同的方法计算正方形的面积,就可以得到直角三角形的三边的数量关系:a2+b2=c2.这一个数量关系,我们叫做“勾股定理”,请你利用图4来证明勾股定理,即a2+b2=c2.
(4)如图5,在Rt△ABC中,∠ACB=90°,CD是AB边上高,AC=4,BC=3,求CD的长度.
第1-3章阶段检测卷-2024-2025学年数学八年级上册北师大版
参考答案与试题解析
一.选择题(共8小题)
1.(2024秋 工业园区校级月考)下列各组数中,不能构成直角三角形三边的是( )
A.3,4,5 B.6,8,10 C.7,24,25 D.8,12,15
【解答】解:A、32+42=25=52,能作为直角三角形的三边,故此选项不符合题意;
B、62+82=100=102,能作为直角三角形的三边,故此选项不符合题意;
C、72+242=625=252,能作为直角三角形的三边,故此选项不符合题意;
D、82+122=208≠152,不能作为直角三角形的三边,故此选项符合题意;
故选:D.
2.(2024秋 工业园区校级月考)在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB边的最小距离是( )
A. B. C. D.2.5
【解答】解:设点C到AB的最小距离为h,
在Rt△ABC中,∠C=90°,
则有AC2+BC2=AB2,
∵AC=9,BC=12,
∴,
∵,
∴.
故选:C.
3.(2024秋 滕州市月考)如果的平方根是±3,则x的值是( )
A.9 B.﹣9 C.81 D.﹣81
【解答】解:∵的平方根是±3,
∴=(±3)2=9,
∴x=()2=92=81.
故选:C.
4.(2024春 禹城市校级月考)已知,,则( )
A.14.35 B.143.5 C.45.39 D.453.9
【解答】解:∵,
∴.
故选:B.
5.(2023秋 辽阳期末)如图,点A,C都是数轴上的点,AB=AC,则数轴上点C所表示的数为( )
A. B. C. D.
【解答】解:A、B、﹣2处的点构成了直角三角形,
∴AB==,
∵AB=AC,
∴AC=,
∴C点所表示的数为﹣+1,
故选:A.
6.(2024秋 高新区月考)象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益部游戏.如图是一局象棋残局,已知表示棋子“马”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为( )
A.(2,3) B.(2,1) C.(1,2) D.(1,3)
【解答】解:如图所示:棋子“炮”的点的坐标为:(1,3).
故选:D.
7.(2024 绵阳)蝴蝶颜色炫丽,翩翩起舞时非常美丽,深受人们喜爱,它的图案具有对称美,如图,蝴蝶图案关于y轴对称,点M的对应点为M1,若点M的坐标为(﹣2,﹣3),则点M1的坐标为( )
A.(2,﹣3) B.(﹣3,2) C.(﹣2,3) D.(2,3)
【解答】解:由题意得,点M(﹣2,﹣3)与点M1关于y轴对称,
∴点M1的坐标为(2,﹣3).
故选:A.
8.(2024秋 柴桑区月考)如图,这是由3个正方形和2个等腰直角三角形组成的图形.若正方形A的面积为24,则正方形B的面积为( )
A.4 B.6 C.8 D.12
【解答】解:由题意可得:DE=DF,GF=GH,
∴EF2=DE2+DF2=2DE2,FH2=GF2+GH2=2GF2,
∵正方形A的面积为24,
∴FH2=24=2GF2,则GF2=12,
∴正方形C的面积为12,
∴EF2=12=2DE2,则DE2=6,
∴正方形B的面积为6.
故选:B.
二.填空题(共8小题)
9.(2024秋 临汾月考)请写出一个大于3小于4的最简二次根式 (答案不唯一) .
【解答】解:∵9<10<16,
即32<10<42,
∴,
∴符合条件的最简二次根式可以是:.
故答案为:(答案不唯一).
10.(2024秋 姑苏区校级月考)某正数的平方根分别是2a+1和a+5,则a= ﹣2 .
【解答】解:根据题意,得:2a+1+a+5=0,
解得:a=﹣2.
故答案为:﹣2.
11.(2024秋 永修县校级月考)用“*”表示一种新运算:对于任意正实数a,b,都有,例如,那么5*169= 18 .
【解答】解:原式=+5=13+5=18,
故答案为:18.
12.(2024秋 禅城区校级月考)点M在第四象限,点M到x轴的距离为3,到y轴的距离为4,则M点坐标是 (4,﹣3) .
【解答】解:∵点P在第四象限,到x轴的距离为3,到y轴的距离为4,
∴点P的横坐标是4,纵坐标是﹣3,
∴点P的坐标为(4,﹣3).
故答案为:(4,﹣3).
13.(2024秋 甘井子区校级月考)如图,点A、B分别在x轴、y轴上,OA=OB,分别以点A、B为圆心,以大于长为半径画弧,两弧交于点P.若点P的坐标为(2a,3a﹣4),则a的值为 4 .
【解答】解:由题意得,点P在∠BOA的角平分线上,
∴点P到x轴和y轴的距离相等,
又∵点P的坐标为(2a,3a﹣4),
∴2a=3a﹣4,
∴a=4.
故答案为:4.
14.(2024秋 禅城区校级月考)如图,动点P从点A出发,沿着圆柱的侧面移动到BC的中点S,若BC=8,点P移动的最短距离为5,则圆柱的底面周长为 6 .
【解答】解:圆柱的侧面展开图如图,点P移动的最短距离为AS=5,
根据题意,,∠ABS=90°,
∴,
∴圆柱的底面周长为2AB=6.
故答案为:6.
15.(2024秋 乌拉特前旗校级月考)如图,在△ABC中,AD既是△ABC的高,也是△ABC的中线,且AD=4,AC=5,BD=3,若点P在边AC上移动,则BP的最小值是 4.8 .
【解答】解:在△ABC中,AD既是△ABC的高,也是△ABC的中线,且AC=5,AD=4,BD=3,
∴BC=2BD=6,
当BP的值最小时,BP⊥AC,
∴,
∴4×6=5BP,
∴BP=4.8,
∴BP的最小值是4.8.
故答案为:4.8.
16.(2024春 白云区期末)如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒,当△ABP为等腰三角形时,t的取值为 5或t=8或t= .
【解答】解:在Rt△ABC中,BC2=AB2﹣AC2=52﹣32=16,
∴BC=4(cm);
①当AB=BP时,如图1,t=5;
②当AB=AP时,如图2,BP=2BC=8cm,t=8;
③当BP=AP时,如图3,AP=BP=tcm,CP=(4﹣t)cm,AC=3cm,
在Rt△ACP中,AP2=AC2+CP2,
所以t2=32+(4﹣t)2,
解得:t=,
综上所述:当△ABP为等腰三角形时,t=5或t=8或t=.
故答案为:5或t=8或t=.
三.解答题(共7小题)
17.(2024秋 郸城县月考)计算:.
【解答】解:
=6﹣2﹣2+3
=5.
18.(2024秋 永修县校级月考)已知:2x﹣1和4x+3是m的两个不同的平方根
(1)求x,m的值.
(2)求1﹣9x的平方根.
【解答】解:(1)2x﹣1+4x+3=0,
解得:,
∴m=(2x﹣1)2=[2×]2=;
(2)∵,
∴,
∵4的平方根为±2,
∴1﹣9x的平方根为±2.
19.(2024秋 雁塔区校级月考)材料:2.5的整数部分是2,小数部分是0.5,小数部分可以看成是2.5﹣2得来的,类比来看,是无理数,而,所以的整数部分是1,于是可用来表示的小数部分.
根据以上材料,完成下列问题:
(1)的整数部分是 4 ,小数部分是 ﹣4 ;
(2)也是夹在相邻两个整数之间的,可以表示为,求a+b的平方根.
【解答】解:(1)∵,
∴的整数部分是4,小数部分是,
故答案为:4,;
(2)∵1<3<4,
∴,
∴,
又,
∴a=4,b=5,
∴a+b=9,
∴a+b的平方根为±3.
20.(2024秋 天长市月考)在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2),若x2﹣x1=y2﹣y1≠0,则称点A与点B互为“对角点”.例如:A(﹣1,3),B(2,6),因为2﹣(﹣1)=6﹣3≠0,所以点A与点B互为“对角点”.
(1)若点A的坐标是(4,﹣2),分别判断点B1(2,0),B2(﹣1,﹣7),B3(0,﹣6)是否为点A的“对角点”,并说明理由;
(2)若点A的坐标是(﹣2,4),其“对角点”B在坐标轴上,求点B的坐标.
【解答】解:(1)点B1(2,0)不是点A的“对角点”,B2(﹣1,﹣7),B3(0,﹣6)是点A的“对角点”,
理由:
∵2﹣4≠0﹣(﹣2),
∴点B1(2,0)不是点A的“对角点”;
∵﹣1﹣4=﹣7﹣(﹣2)=﹣5≠0,
∴点B2(﹣1,﹣7)是点A的“对角点”;
∵0﹣4=﹣6﹣(﹣2)=﹣4≠0,
∴点B3(0,﹣6)是点A的“对角点”;
(2)①当点B在x轴上时,
设B(x,0),由题意得,x﹣(﹣2)=0﹣4,
解得x=﹣6,
∴B(﹣6,0);
②当点B在y轴上时,
设B(0,y),由题意得,0﹣(﹣2)=y﹣4,
解得y=6,
∴B(0,6),
综上所述,点B的坐标为(﹣6,0)或(0,6).
21.(2024春 民勤县期末)如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足.
(1)填空:a= ﹣1 ,b= 3 ;
(2)若在第三象限内有一点M(﹣2,m),用含m的式子表示△ABM的面积;
(3)在(2)条件下,线段BM与y轴相交于C(0,﹣),当时,点P是y轴上的动点,当满足△PBM的面积是△ABM的面积的2倍时,求点P的坐标.
【解答】解:(1)∵a、b满足+(b﹣3)2=0,
∴a+1=0,且b﹣3=0,
∴a=﹣1,b=3,
故答案为:﹣1,3;
(2)∵a=﹣1,b=3,
∴A(﹣1,0),B(3,0),
∴AB=4,
∵M(﹣2,m),且M在第三象限,
∴m<0,
∴△ABM的面积=×4×(﹣m)=﹣2m;
(3)当m=﹣时,
则M(﹣2,﹣),S△ABM=﹣2m=﹣2×(﹣)=3,
∵△PBM的面积=△ABM的面积的2倍=6,
∵△PBM的面积=△MPC的面积+△BPC的面积=PC×2+PC×3=6,
解得:PC=,
∵C(0,﹣),
∴OC=,
当点P在点C的下方时,P(0,﹣﹣),即P(0,﹣);
当点P在点C的上方时,P(0,﹣),即P(0,);
综上所述,点P的坐标为(0,﹣)或(0,).
22.(2024秋 芗城区校级月考)某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,已知∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m.
(1)△ABC是直角三角形吗,为什么?
(2)若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
【解答】解:(1)是,理由如下:
连接AC,
∵∠ADC=90°,AD=4m,CD=3m,
∴AC===5(m),
∵AB=13m,BC=12m,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(2)S四边形ABCD=S△ABC﹣S△ADC
=
=24m2;
∴24×200=4800(元);
答:学校需要投入4800元买草皮.
23.(2024春 长清区期中)(1)计算:(2a+b)(a+b)= 2a2+3ab+b2 ;
(2)图形是一种重要的数学语言,它直观形象,我们可以用几何图形的面积来解释一些代数中的等量关系.例如:上面的计算是否正确我们可以通过图1来进行验证和解释.请同学们分别写出图2、图3能解释的乘法公式:
图2: (a﹣b)2=a2﹣2ab+b2 ;
图3: (a+b )(a﹣b)=a2﹣b2 ;
(3)利用几何图形的面积,我们还可以去探究一些其它的等量关系:
做4个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,再做1个长分别为c的正方形,把它们按图4所示的方式拼成一个大正方形.试用不同的方法计算正方形的面积,就可以得到直角三角形的三边的数量关系:a2+b2=c2.这一个数量关系,我们叫做“勾股定理”,请你利用图4来证明勾股定理,即a2+b2=c2.
(4)如图5,在Rt△ABC中,∠ACB=90°,CD是AB边上高,AC=4,BC=3,求CD的长度.
【解答】解:(1)原式=2a2+2ab+ab+b2=2a2+3ab+b2.
故答案为:2a2+3ab+b2.
(2)(a﹣b)2=a2﹣2ab+b2,
(a+b )(a﹣b)=a2﹣b2,
故答案为:(a﹣b)2=a2﹣2ab+b2;(a+b )(a﹣b)=a2﹣b2.
(3)在图4中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,即 ,
化简,得 a2+b2=c2.
(4)在 Rt△ABC中,
∵∠ACB=90°,
∴由勾股定理得AB2=AC2+BC2=42+32=25
∴AB=5,
∵CD⊥AB,
∴,
∴.
一.选择题(共8小题)
1.(2024秋 工业园区校级月考)下列各组数中,不能构成直角三角形三边的是( )
A.3,4,5 B.6,8,10 C.7,24,25 D.8,12,15
2.(2024秋 工业园区校级月考)在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB边的最小距离是( )
A. B. C. D.2.5
3.(2024秋 滕州市月考)如果的平方根是±3,则x的值是( )
A.9 B.﹣9 C.81 D.﹣81
4.(2024春 禹城市校级月考)已知,,则( )
A.14.35 B.143.5 C.45.39 D.453.9
5.(2023秋 辽阳期末)如图,点A,C都是数轴上的点,AB=AC,则数轴上点C所表示的数为( )
A. B. C. D.
6.(2024秋 高新区月考)象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益部游戏.如图是一局象棋残局,已知表示棋子“马”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为( )
A.(2,3) B.(2,1) C.(1,2) D.(1,3)
7.(2024 绵阳)蝴蝶颜色炫丽,翩翩起舞时非常美丽,深受人们喜爱,它的图案具有对称美,如图,蝴蝶图案关于y轴对称,点M的对应点为M1,若点M的坐标为(﹣2,﹣3),则点M1的坐标为( )
A.(2,﹣3) B.(﹣3,2) C.(﹣2,3) D.(2,3)
8.(2024秋 柴桑区月考)如图,这是由3个正方形和2个等腰直角三角形组成的图形.若正方形A的面积为24,则正方形B的面积为( )
A.4 B.6 C.8 D.12
二.填空题(共8小题)
9.(2024秋 临汾月考)请写出一个大于3小于4的最简二次根式 .
10.(2024秋 姑苏区校级月考)某正数的平方根分别是2a+1和a+5,则a= .
11.(2024秋 永修县校级月考)用“*”表示一种新运算:对于任意正实数a,b,都有,例如,那么5*169= .
12.(2024秋 禅城区校级月考)点M在第四象限,点M到x轴的距离为3,到y轴的距离为4,则M点坐标是 .
13.(2024秋 甘井子区校级月考)如图,点A、B分别在x轴、y轴上,OA=OB,分别以点A、B为圆心,以大于长为半径画弧,两弧交于点P.若点P的坐标为(2a,3a﹣4),则a的值为 .
14.(2024秋 禅城区校级月考)如图,动点P从点A出发,沿着圆柱的侧面移动到BC的中点S,若BC=8,点P移动的最短距离为5,则圆柱的底面周长为 .
15.(2024秋 乌拉特前旗校级月考)如图,在△ABC中,AD既是△ABC的高,也是△ABC的中线,且AD=4,AC=5,BD=3,若点P在边AC上移动,则BP的最小值是 .
16.(2024春 白云区期末)如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒,当△ABP为等腰三角形时,t的取值为 .
三.解答题(共7小题)
17.(2024秋 郸城县月考)计算:.
18.(2024秋 永修县校级月考)已知:2x﹣1和4x+3是m的两个不同的平方根
(1)求x,m的值.
(2)求1﹣9x的平方根.
19.(2024秋 雁塔区校级月考)材料:2.5的整数部分是2,小数部分是0.5,小数部分可以看成是2.5﹣2得来的,类比来看,是无理数,而,所以的整数部分是1,于是可用来表示的小数部分.
根据以上材料,完成下列问题:
(1)的整数部分是 ,小数部分是 ;
(2)也是夹在相邻两个整数之间的,可以表示为,求a+b的平方根.
20.(2024秋 天长市月考)在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2),若x2﹣x1=y2﹣y1≠0,则称点A与点B互为“对角点”.例如:A(﹣1,3),B(2,6),因为2﹣(﹣1)=6﹣3≠0,所以点A与点B互为“对角点”.
(1)若点A的坐标是(4,﹣2),分别判断点B1(2,0),B2(﹣1,﹣7),B3(0,﹣6)是否为点A的“对角点”,并说明理由;
(2)若点A的坐标是(﹣2,4),其“对角点”B在坐标轴上,求点B的坐标.
21.(2024春 民勤县期末)如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足.
(1)填空:a= ,b= ;
(2)若在第三象限内有一点M(﹣2,m),用含m的式子表示△ABM的面积;
(3)在(2)条件下,线段BM与y轴相交于C(0,﹣),当时,点P是y轴上的动点,当满足△PBM的面积是△ABM的面积的2倍时,求点P的坐标.
22.(2024秋 芗城区校级月考)某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,已知∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m.
(1)△ABC是直角三角形吗,为什么?
(2)若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
23.(2024春 长清区期中)(1)计算:(2a+b)(a+b)= ;
(2)图形是一种重要的数学语言,它直观形象,我们可以用几何图形的面积来解释一些代数中的等量关系.例如:上面的计算是否正确我们可以通过图1来进行验证和解释.请同学们分别写出图2、图3能解释的乘法公式:
图2: ;
图3: ;
(3)利用几何图形的面积,我们还可以去探究一些其它的等量关系:
做4个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,再做1个长分别为c的正方形,把它们按图4所示的方式拼成一个大正方形.试用不同的方法计算正方形的面积,就可以得到直角三角形的三边的数量关系:a2+b2=c2.这一个数量关系,我们叫做“勾股定理”,请你利用图4来证明勾股定理,即a2+b2=c2.
(4)如图5,在Rt△ABC中,∠ACB=90°,CD是AB边上高,AC=4,BC=3,求CD的长度.
第1-3章阶段检测卷-2024-2025学年数学八年级上册北师大版
参考答案与试题解析
一.选择题(共8小题)
1.(2024秋 工业园区校级月考)下列各组数中,不能构成直角三角形三边的是( )
A.3,4,5 B.6,8,10 C.7,24,25 D.8,12,15
【解答】解:A、32+42=25=52,能作为直角三角形的三边,故此选项不符合题意;
B、62+82=100=102,能作为直角三角形的三边,故此选项不符合题意;
C、72+242=625=252,能作为直角三角形的三边,故此选项不符合题意;
D、82+122=208≠152,不能作为直角三角形的三边,故此选项符合题意;
故选:D.
2.(2024秋 工业园区校级月考)在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB边的最小距离是( )
A. B. C. D.2.5
【解答】解:设点C到AB的最小距离为h,
在Rt△ABC中,∠C=90°,
则有AC2+BC2=AB2,
∵AC=9,BC=12,
∴,
∵,
∴.
故选:C.
3.(2024秋 滕州市月考)如果的平方根是±3,则x的值是( )
A.9 B.﹣9 C.81 D.﹣81
【解答】解:∵的平方根是±3,
∴=(±3)2=9,
∴x=()2=92=81.
故选:C.
4.(2024春 禹城市校级月考)已知,,则( )
A.14.35 B.143.5 C.45.39 D.453.9
【解答】解:∵,
∴.
故选:B.
5.(2023秋 辽阳期末)如图,点A,C都是数轴上的点,AB=AC,则数轴上点C所表示的数为( )
A. B. C. D.
【解答】解:A、B、﹣2处的点构成了直角三角形,
∴AB==,
∵AB=AC,
∴AC=,
∴C点所表示的数为﹣+1,
故选:A.
6.(2024秋 高新区月考)象棋在中国有着三千多年的历史,由于用具简单,趣味性强,成为流行极为广泛的益部游戏.如图是一局象棋残局,已知表示棋子“马”和“車”的点的坐标分别为(4,3),(﹣2,1),则表示棋子“炮”的点的坐标为( )
A.(2,3) B.(2,1) C.(1,2) D.(1,3)
【解答】解:如图所示:棋子“炮”的点的坐标为:(1,3).
故选:D.
7.(2024 绵阳)蝴蝶颜色炫丽,翩翩起舞时非常美丽,深受人们喜爱,它的图案具有对称美,如图,蝴蝶图案关于y轴对称,点M的对应点为M1,若点M的坐标为(﹣2,﹣3),则点M1的坐标为( )
A.(2,﹣3) B.(﹣3,2) C.(﹣2,3) D.(2,3)
【解答】解:由题意得,点M(﹣2,﹣3)与点M1关于y轴对称,
∴点M1的坐标为(2,﹣3).
故选:A.
8.(2024秋 柴桑区月考)如图,这是由3个正方形和2个等腰直角三角形组成的图形.若正方形A的面积为24,则正方形B的面积为( )
A.4 B.6 C.8 D.12
【解答】解:由题意可得:DE=DF,GF=GH,
∴EF2=DE2+DF2=2DE2,FH2=GF2+GH2=2GF2,
∵正方形A的面积为24,
∴FH2=24=2GF2,则GF2=12,
∴正方形C的面积为12,
∴EF2=12=2DE2,则DE2=6,
∴正方形B的面积为6.
故选:B.
二.填空题(共8小题)
9.(2024秋 临汾月考)请写出一个大于3小于4的最简二次根式 (答案不唯一) .
【解答】解:∵9<10<16,
即32<10<42,
∴,
∴符合条件的最简二次根式可以是:.
故答案为:(答案不唯一).
10.(2024秋 姑苏区校级月考)某正数的平方根分别是2a+1和a+5,则a= ﹣2 .
【解答】解:根据题意,得:2a+1+a+5=0,
解得:a=﹣2.
故答案为:﹣2.
11.(2024秋 永修县校级月考)用“*”表示一种新运算:对于任意正实数a,b,都有,例如,那么5*169= 18 .
【解答】解:原式=+5=13+5=18,
故答案为:18.
12.(2024秋 禅城区校级月考)点M在第四象限,点M到x轴的距离为3,到y轴的距离为4,则M点坐标是 (4,﹣3) .
【解答】解:∵点P在第四象限,到x轴的距离为3,到y轴的距离为4,
∴点P的横坐标是4,纵坐标是﹣3,
∴点P的坐标为(4,﹣3).
故答案为:(4,﹣3).
13.(2024秋 甘井子区校级月考)如图,点A、B分别在x轴、y轴上,OA=OB,分别以点A、B为圆心,以大于长为半径画弧,两弧交于点P.若点P的坐标为(2a,3a﹣4),则a的值为 4 .
【解答】解:由题意得,点P在∠BOA的角平分线上,
∴点P到x轴和y轴的距离相等,
又∵点P的坐标为(2a,3a﹣4),
∴2a=3a﹣4,
∴a=4.
故答案为:4.
14.(2024秋 禅城区校级月考)如图,动点P从点A出发,沿着圆柱的侧面移动到BC的中点S,若BC=8,点P移动的最短距离为5,则圆柱的底面周长为 6 .
【解答】解:圆柱的侧面展开图如图,点P移动的最短距离为AS=5,
根据题意,,∠ABS=90°,
∴,
∴圆柱的底面周长为2AB=6.
故答案为:6.
15.(2024秋 乌拉特前旗校级月考)如图,在△ABC中,AD既是△ABC的高,也是△ABC的中线,且AD=4,AC=5,BD=3,若点P在边AC上移动,则BP的最小值是 4.8 .
【解答】解:在△ABC中,AD既是△ABC的高,也是△ABC的中线,且AC=5,AD=4,BD=3,
∴BC=2BD=6,
当BP的值最小时,BP⊥AC,
∴,
∴4×6=5BP,
∴BP=4.8,
∴BP的最小值是4.8.
故答案为:4.8.
16.(2024春 白云区期末)如图,在Rt△ABC中,∠ACB=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为t秒,当△ABP为等腰三角形时,t的取值为 5或t=8或t= .
【解答】解:在Rt△ABC中,BC2=AB2﹣AC2=52﹣32=16,
∴BC=4(cm);
①当AB=BP时,如图1,t=5;
②当AB=AP时,如图2,BP=2BC=8cm,t=8;
③当BP=AP时,如图3,AP=BP=tcm,CP=(4﹣t)cm,AC=3cm,
在Rt△ACP中,AP2=AC2+CP2,
所以t2=32+(4﹣t)2,
解得:t=,
综上所述:当△ABP为等腰三角形时,t=5或t=8或t=.
故答案为:5或t=8或t=.
三.解答题(共7小题)
17.(2024秋 郸城县月考)计算:.
【解答】解:
=6﹣2﹣2+3
=5.
18.(2024秋 永修县校级月考)已知:2x﹣1和4x+3是m的两个不同的平方根
(1)求x,m的值.
(2)求1﹣9x的平方根.
【解答】解:(1)2x﹣1+4x+3=0,
解得:,
∴m=(2x﹣1)2=[2×]2=;
(2)∵,
∴,
∵4的平方根为±2,
∴1﹣9x的平方根为±2.
19.(2024秋 雁塔区校级月考)材料:2.5的整数部分是2,小数部分是0.5,小数部分可以看成是2.5﹣2得来的,类比来看,是无理数,而,所以的整数部分是1,于是可用来表示的小数部分.
根据以上材料,完成下列问题:
(1)的整数部分是 4 ,小数部分是 ﹣4 ;
(2)也是夹在相邻两个整数之间的,可以表示为,求a+b的平方根.
【解答】解:(1)∵,
∴的整数部分是4,小数部分是,
故答案为:4,;
(2)∵1<3<4,
∴,
∴,
又,
∴a=4,b=5,
∴a+b=9,
∴a+b的平方根为±3.
20.(2024秋 天长市月考)在平面直角坐标系xOy中,点A(x1,y1),B(x2,y2),若x2﹣x1=y2﹣y1≠0,则称点A与点B互为“对角点”.例如:A(﹣1,3),B(2,6),因为2﹣(﹣1)=6﹣3≠0,所以点A与点B互为“对角点”.
(1)若点A的坐标是(4,﹣2),分别判断点B1(2,0),B2(﹣1,﹣7),B3(0,﹣6)是否为点A的“对角点”,并说明理由;
(2)若点A的坐标是(﹣2,4),其“对角点”B在坐标轴上,求点B的坐标.
【解答】解:(1)点B1(2,0)不是点A的“对角点”,B2(﹣1,﹣7),B3(0,﹣6)是点A的“对角点”,
理由:
∵2﹣4≠0﹣(﹣2),
∴点B1(2,0)不是点A的“对角点”;
∵﹣1﹣4=﹣7﹣(﹣2)=﹣5≠0,
∴点B2(﹣1,﹣7)是点A的“对角点”;
∵0﹣4=﹣6﹣(﹣2)=﹣4≠0,
∴点B3(0,﹣6)是点A的“对角点”;
(2)①当点B在x轴上时,
设B(x,0),由题意得,x﹣(﹣2)=0﹣4,
解得x=﹣6,
∴B(﹣6,0);
②当点B在y轴上时,
设B(0,y),由题意得,0﹣(﹣2)=y﹣4,
解得y=6,
∴B(0,6),
综上所述,点B的坐标为(﹣6,0)或(0,6).
21.(2024春 民勤县期末)如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足.
(1)填空:a= ﹣1 ,b= 3 ;
(2)若在第三象限内有一点M(﹣2,m),用含m的式子表示△ABM的面积;
(3)在(2)条件下,线段BM与y轴相交于C(0,﹣),当时,点P是y轴上的动点,当满足△PBM的面积是△ABM的面积的2倍时,求点P的坐标.
【解答】解:(1)∵a、b满足+(b﹣3)2=0,
∴a+1=0,且b﹣3=0,
∴a=﹣1,b=3,
故答案为:﹣1,3;
(2)∵a=﹣1,b=3,
∴A(﹣1,0),B(3,0),
∴AB=4,
∵M(﹣2,m),且M在第三象限,
∴m<0,
∴△ABM的面积=×4×(﹣m)=﹣2m;
(3)当m=﹣时,
则M(﹣2,﹣),S△ABM=﹣2m=﹣2×(﹣)=3,
∵△PBM的面积=△ABM的面积的2倍=6,
∵△PBM的面积=△MPC的面积+△BPC的面积=PC×2+PC×3=6,
解得:PC=,
∵C(0,﹣),
∴OC=,
当点P在点C的下方时,P(0,﹣﹣),即P(0,﹣);
当点P在点C的上方时,P(0,﹣),即P(0,);
综上所述,点P的坐标为(0,﹣)或(0,).
22.(2024秋 芗城区校级月考)某中学有一块四边形的空地ABCD,学校计划在空地上种植草皮,已知∠ADC=90°,AD=4m,CD=3m,AB=13m,BC=12m.
(1)△ABC是直角三角形吗,为什么?
(2)若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
【解答】解:(1)是,理由如下:
连接AC,
∵∠ADC=90°,AD=4m,CD=3m,
∴AC===5(m),
∵AB=13m,BC=12m,
∴AC2+BC2=AB2,
∴△ABC是直角三角形;
(2)S四边形ABCD=S△ABC﹣S△ADC
=
=24m2;
∴24×200=4800(元);
答:学校需要投入4800元买草皮.
23.(2024春 长清区期中)(1)计算:(2a+b)(a+b)= 2a2+3ab+b2 ;
(2)图形是一种重要的数学语言,它直观形象,我们可以用几何图形的面积来解释一些代数中的等量关系.例如:上面的计算是否正确我们可以通过图1来进行验证和解释.请同学们分别写出图2、图3能解释的乘法公式:
图2: (a﹣b)2=a2﹣2ab+b2 ;
图3: (a+b )(a﹣b)=a2﹣b2 ;
(3)利用几何图形的面积,我们还可以去探究一些其它的等量关系:
做4个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,再做1个长分别为c的正方形,把它们按图4所示的方式拼成一个大正方形.试用不同的方法计算正方形的面积,就可以得到直角三角形的三边的数量关系:a2+b2=c2.这一个数量关系,我们叫做“勾股定理”,请你利用图4来证明勾股定理,即a2+b2=c2.
(4)如图5,在Rt△ABC中,∠ACB=90°,CD是AB边上高,AC=4,BC=3,求CD的长度.
【解答】解:(1)原式=2a2+2ab+ab+b2=2a2+3ab+b2.
故答案为:2a2+3ab+b2.
(2)(a﹣b)2=a2﹣2ab+b2,
(a+b )(a﹣b)=a2﹣b2,
故答案为:(a﹣b)2=a2﹣2ab+b2;(a+b )(a﹣b)=a2﹣b2.
(3)在图4中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,即 ,
化简,得 a2+b2=c2.
(4)在 Rt△ABC中,
∵∠ACB=90°,
∴由勾股定理得AB2=AC2+BC2=42+32=25
∴AB=5,
∵CD⊥AB,
∴,
∴.
同课章节目录
