第21章 一元二次方程 单元检测卷(含详解)2024-2025学年人教版九年级数学上册
文档属性
| 名称 | 第21章 一元二次方程 单元检测卷(含详解)2024-2025学年人教版九年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 108.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-02 18:13:06 | ||
图片预览




文档简介
第21章一元二次方程检测卷-2024-2025学年数学九年级上册人教版
一.选择题(共6小题)
1.(2023秋 龙泉驿区期末)下列方程中,属于一元二次方程的是( )
A.x﹣2y=1 B. C.x2﹣2y+4=0 D.x2﹣2x+1=0
2.(2024秋 东城区校级月考)关于x的一元二次方程2x2+bx﹣1=0的根的情况是( )
A.实数根的个数由b的值确定
B.有两个不相等的实数根
C.有两个相等的实数根
D.没有实数根
3.(2023秋 旌阳区期末)若一元二次方程ax2+bx+c=0(a≠0)的一个根是x=1,则a+b+c的值是( )
A.0 B.﹣1 C.1 D.不能确定
4.(2024春 鹿城区校级期中)王老师购买了2304张签名卡,在毕业典礼上,他向每位同学赠送了一张签名卡,每位同学间也互赠了一张签名卡,签名卡恰好用完,设班级有x名学生,则下列方程成立的是( )
A. B.
C.x(x﹣1)+x=2304 D.x(x﹣1)=2304
5.(2024秋 裕华区校级月考)嘉嘉和琪琪一起写作业,在解一道一元二次方程时,嘉嘉在化简过程中写错了常数项,因而得到方程的两个根是﹣1和﹣5;琪琪在化简过程中写错了一次项的系数,因而得到方程的两个根是3和2.则正确的方程是( )
A.x2+6x+5=0 B.x2﹣5x+6=0 C.x2﹣5x+5=0 D.x2+6x+6=0
6.(2024秋 阿荣旗校级月考)如图,在长70m,宽40m的长方形花园中,欲修宽度相等的观赏路(如阴影部分所示),要使观赏路面积占总面积的,若设路宽为x m,则x应满足的方程是( )
A.(40﹣x)(70﹣x)=350
B.(40﹣2x)(70﹣3x)=2450
C.(40﹣2x)(70﹣3x)=350
D.(40﹣x)(70﹣x)=2150
二.填空题(共8小题)
7.(2023秋 宣汉县期末)已知关于x的方程(a+1)x2﹣2x+3=0有实数根,则整数a的最大值是 .
8.(2024 常州二模)已知m为方程x2﹣3x﹣6=0的一个根,则代数式﹣m2+3m﹣6的值是 .
9.(2024秋 建邺区校级期中)若关于x的一元二次方程ax2+bx+c=0(a、b、c都为有理数)的一个解是x1=4﹣2,则方程的另一个解是 .
10.(2024秋 东昌府区校级月考)参加会议的人两两彼此握手,一共握了55次手,那么一共有 人参加会议.
11.(2024秋 永寿县校级月考)一元二次方程(x﹣1)2=x+2的一般形式为 .(二次项的系数为正数)
12.(2024秋 即墨区校级月考)如图,王师傅要建一个矩形羊圈,羊圈的一边利用长为18m的住房墙,另外三边用45m长的彩钢围成,为了方便进出,在垂直于住房墙的一边要留出1m安装木门.若要使羊圈的面积为224m2,则所围矩形与墙垂直的一边长为 .
13.(2024秋 临湘市校级月考)《田亩比类乘除捷法》中记载了一道题:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步.”译文:一个矩形的面积为864平方步,宽比长少12步,问宽和长各多少步?设矩形的宽为x步,由题意,可列方程为 .
14.(2024秋 裕华区校级月考)若关于x的一元二次方程(m+4)x2﹣4x+1=0有两个不相等的实数根,则m的取值范围是 .
三.解答题(共6小题)
15.(2024秋 榆次区校级月考)解下列方程:
(1)(2x+5)(x﹣6)=0;
(2)2x2﹣4x﹣3=0;
(3)(2x+3)2=(3x+2)2;
(4)3y2﹣6y﹣5=0(用配方法求解).
16.(2024秋 双峰县月考)已知一元二次方程ax2+bx+c=0(a≠0).
(1)如果方程有一个根是1,那么a、b、c之间有什么关系?
(2)如果方程有一个根是﹣1,那么a、b、c之间有什么关系?
(3)如果方程有一个根是0,那么方程的系数或常数项有什么特征?
17.(2024秋 兴庆区校级月考)关于x的一元二次方程x2﹣3x+2=0.
(1)试判断该方程根的情况;
(2)若a,b是该方程的两个实数根,化简并求下面式子的值:.
18.(2024秋 德州月考)小明在解一元二次方程时,发现这样一种解法.
如:解方程x(x+4)=6
解:原方程可变形为[(x+2)﹣2][(x+2)+2]=6
∴(x+2)2﹣22=6,
∴(x+2)2=10
直接开平方整理得:;
我们称小明的这种解法为“平均数法”
(1)下面是小明用“平均数法”解方程(x+3)(x+7)=5时写的解题过程.
解:原方程变形为[(x+a)﹣b][(x+a)+b]=5
∴(x+a)2﹣b2=5,
∴(x+a)2=5+b2
直接开平方整理得:x1=c;x2=d
上述过程中的a= ;b= ;c= ;d= .
(2)请用“平均数法”解方程:(x﹣5)(x+3)=6.
19.(2024秋 增城区校级月考)为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2018年市政府共投资4亿元人民币建设了廉租房,2020年计划投资9亿元人民币建设廉租房,若每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)请问2021年建设廉租房投资多少亿?
20.(2024秋 海州区校级月考)如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
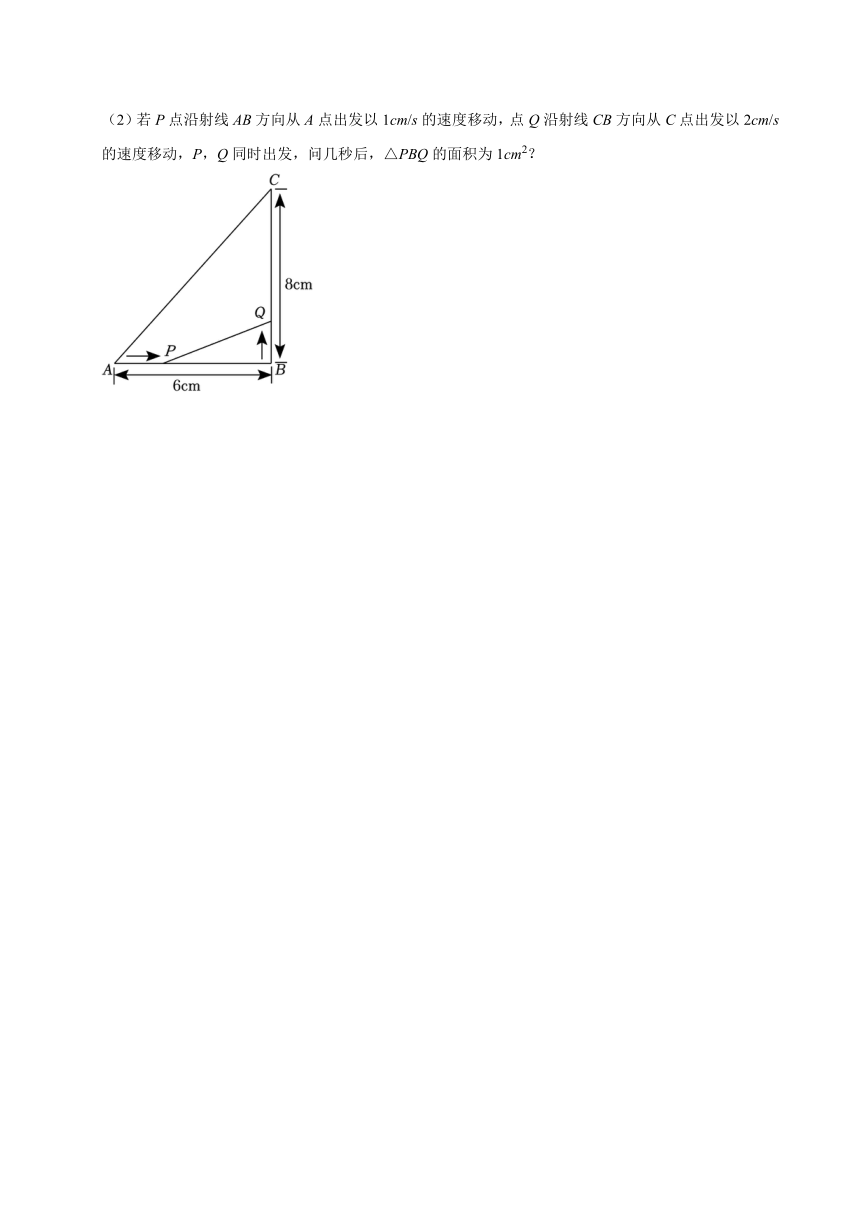
(2)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1cm2?
第21章一元二次方程检测卷-2024-2025学年数学九年级上册人教版
参考答案与试题解析
一.选择题(共6小题)
1.(2023秋 龙泉驿区期末)下列方程中,属于一元二次方程的是( )
A.x﹣2y=1 B. C.x2﹣2y+4=0 D.x2﹣2x+1=0
【解答】解:A.方程x﹣2y=1是二元一次方程,选项A不符合题意;
B.方程x2+3=是分式方程,选项B不符合题意;
C.方程x2﹣2y+4=0是二元二次方程,选项C不符合题意;
D.方程x2﹣2x+1=0是一元二次方程,选项D符合题意.
故选:D.
2.(2024秋 东城区校级月考)关于x的一元二次方程2x2+bx﹣1=0的根的情况是( )
A.实数根的个数由b的值确定
B.有两个不相等的实数根
C.有两个相等的实数根
D.没有实数根
【解答】解:由题知,
Δ=b2﹣4×2×(﹣1)=b2+8≥8>0,
所以此一元二次方程有两个不相等的实数根.
故选:B.
3.(2023秋 旌阳区期末)若一元二次方程ax2+bx+c=0(a≠0)的一个根是x=1,则a+b+c的值是( )
A.0 B.﹣1 C.1 D.不能确定
【解答】解:把x=1代入方程得:a+b+c=0,
故选:A.
4.(2024春 鹿城区校级期中)王老师购买了2304张签名卡,在毕业典礼上,他向每位同学赠送了一张签名卡,每位同学间也互赠了一张签名卡,签名卡恰好用完,设班级有x名学生,则下列方程成立的是( )
A. B.
C.x(x﹣1)+x=2304 D.x(x﹣1)=2304
【解答】解:根据题意,王老师共赠送了x张签名卡,同学之间共赠送了x(x﹣1)张签名卡,
∴x(x﹣1)+x=2304;
故选:C.
5.(2024秋 裕华区校级月考)嘉嘉和琪琪一起写作业,在解一道一元二次方程时,嘉嘉在化简过程中写错了常数项,因而得到方程的两个根是﹣1和﹣5;琪琪在化简过程中写错了一次项的系数,因而得到方程的两个根是3和2.则正确的方程是( )
A.x2+6x+5=0 B.x2﹣5x+6=0 C.x2﹣5x+5=0 D.x2+6x+6=0
【解答】解:∵嘉嘉在化简过程中写错了常数项,因而得到方程的两个根是﹣1和﹣5,
∴两根之和﹣=﹣1+(﹣5)=﹣6,
∴当a=1时,b=6;
∵琪琪在化简过程中写错了一次项的系数,因而得到方程的两个根是3和2,
∴两根之积=﹣1×(﹣5)=5,
∴当a=1时,c=5,
∴正确的方程是x2+6x+5=0.
故选:A.
6.(2024秋 阿荣旗校级月考)如图,在长70m,宽40m的长方形花园中,欲修宽度相等的观赏路(如阴影部分所示),要使观赏路面积占总面积的,若设路宽为x m,则x应满足的方程是( )
A.(40﹣x)(70﹣x)=350
B.(40﹣2x)(70﹣3x)=2450
C.(40﹣2x)(70﹣3x)=350
D.(40﹣x)(70﹣x)=2150
【解答】解:∵设路宽为x m,所剩下的观赏面积的宽为(40﹣2x)m,长为(70﹣3x)m,要使观赏路面积占总面积,
∴,
即(40﹣2x)(70﹣3x)=2450.
故选:B.
二.填空题(共8小题)
7.(2023秋 宣汉县期末)已知关于x的方程(a+1)x2﹣2x+3=0有实数根,则整数a的最大值是 ﹣1 .
【解答】解:当a+1=0时,原方程为﹣2x+3=0,解得x=,
∴a=﹣1符合题意;
当a+1≠0时,Δ=(﹣2)2﹣4×(a+1)×3≥0,
解得:a≤﹣,
∴a≤﹣且a≠﹣1.
综上所述,a≤﹣.
又∵a为整数,
∴a的最大值为﹣1.
故答案为:﹣1.
8.(2024 常州二模)已知m为方程x2﹣3x﹣6=0的一个根,则代数式﹣m2+3m﹣6的值是 ﹣12 .
【解答】解:∵m为方程x2﹣3x﹣6=0的一个根,
∴m2﹣3m=6,
∴﹣m2+3m﹣6=﹣(m2﹣3m)﹣6=﹣6﹣6=﹣12.
故答案为:﹣12.
9.(2024秋 建邺区校级期中)若关于x的一元二次方程ax2+bx+c=0(a、b、c都为有理数)的一个解是x1=4﹣2,则方程的另一个解是 .
【解答】解:设方程的另一个根为x2,
∵关于x的一元二次方程ax2+bx+c=0中,a、b、c是有理数,
∴、都是有理数,
∴x1+x2,x1 x2均是有理数,
∵方程的一个根是,
∴方程的另一个根是,
故答案为:.
10.(2024秋 东昌府区校级月考)参加会议的人两两彼此握手,一共握了55次手,那么一共有 11 人参加会议.
【解答】解:设一共有x人参加会议,
则x(x﹣1)=55,
解得x1=11,x2=﹣10(不合题意舍去);
答:一共有11人.
故答案为:11.
11.(2024秋 永寿县校级月考)一元二次方程(x﹣1)2=x+2的一般形式为 x2﹣3x﹣1=0 .(二次项的系数为正数)
【解答】解:∵(x﹣1)2=x+2,
∴x2﹣2x+1=x+2,
∴x2﹣2x+1﹣x﹣2=0,
∴x2﹣3x﹣1=0,
∴一元二次方程(x﹣1)2=x+2的一般形式为x2﹣3x﹣1=0.
故答案为:x2﹣3x﹣1=0.
12.(2024秋 即墨区校级月考)如图,王师傅要建一个矩形羊圈,羊圈的一边利用长为18m的住房墙,另外三边用45m长的彩钢围成,为了方便进出,在垂直于住房墙的一边要留出1m安装木门.若要使羊圈的面积为224m2,则所围矩形与墙垂直的一边长为 16m .
【解答】解:设所围矩形与墙垂直的一边长为x m,
根据题意,得x(45+1﹣2x)=224,
解得x1=7,x2=16,
当x=7时,45+1﹣2x=32>18,不符题意,舍去,
当x=16时,45+1﹣2x=14<18,符合题意,
∴所围矩形与墙垂直的一边长为16m,
故答案为:16m.
13.(2024秋 临湘市校级月考)《田亩比类乘除捷法》中记载了一道题:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步.”译文:一个矩形的面积为864平方步,宽比长少12步,问宽和长各多少步?设矩形的宽为x步,由题意,可列方程为 x(x+12)=864 .
【解答】解:∵矩形的宽为x步,且宽比长少12步,
∴矩形的长为(x+12)步.
依题意,得:x(x+12)=864.
故答案为:x(x+12)=864.
14.(2024秋 裕华区校级月考)若关于x的一元二次方程(m+4)x2﹣4x+1=0有两个不相等的实数根,则m的取值范围是 m<0且m≠﹣4 .
【解答】解:∵关于x的一元二次方程(m+4)x2﹣4x+1=0有两个不相等的实数根,
∴Δ>0且m+4≠0,即(﹣4)2﹣4(m+4)>0且m≠﹣4,
解得m<0且m≠﹣4,
故答案为:m<0且m≠﹣4.
三.解答题(共6小题)
15.(2024秋 榆次区校级月考)解下列方程:
(1)(2x+5)(x﹣6)=0;
(2)2x2﹣4x﹣3=0;
(3)(2x+3)2=(3x+2)2;
(4)3y2﹣6y﹣5=0(用配方法求解).
【解答】解:(1)由题意得2x+5=0或x﹣6=0,
∴,x2=6;
(2)∵a=2,b=﹣4,c=﹣3,
∴Δ=(﹣4)2﹣4×2×(﹣3)=40>0,
∴,
∴,;
(3)开方得2x+3=±(3x+2),
即2x+3=3x+2或2x+3=﹣(3x+2),
∴x1=1,x2=﹣1;
(4)∵3y2﹣6y﹣5=0,
∴,
∴,
∴,
即,
∴,
∴,.
16.(2024秋 双峰县月考)已知一元二次方程ax2+bx+c=0(a≠0).
(1)如果方程有一个根是1,那么a、b、c之间有什么关系?
(2)如果方程有一个根是﹣1,那么a、b、c之间有什么关系?
(3)如果方程有一个根是0,那么方程的系数或常数项有什么特征?
【解答】解:(1)将x=1代入原方程得:a×1+b×1+c=0,
即a+b+c=0;
(2)将x=﹣1代入原方程得:a×(﹣1)2+b×(﹣1)+c=0,
即a﹣b+c=0;
(3)将x=0代入原方程可得:a×0+b×0+c=0,
∴c=0.
17.(2024秋 兴庆区校级月考)关于x的一元二次方程x2﹣3x+2=0.
(1)试判断该方程根的情况;
(2)若a,b是该方程的两个实数根,化简并求下面式子的值:.
【解答】解:(1)∵Δ=(﹣3)2﹣4×2×1=1>0,
∴方程有两个不相等的实数根;
(2)∵a,b是该方程的两个实数根,
∴a+b=3,ab=2,
=
=
=
=
=
=
=;
∵a+b=3,
∴原式=.
18.(2024秋 德州月考)小明在解一元二次方程时,发现这样一种解法.
如:解方程x(x+4)=6
解:原方程可变形为[(x+2)﹣2][(x+2)+2]=6
∴(x+2)2﹣22=6,
∴(x+2)2=10
直接开平方整理得:;
我们称小明的这种解法为“平均数法”
(1)下面是小明用“平均数法”解方程(x+3)(x+7)=5时写的解题过程.
解:原方程变形为[(x+a)﹣b][(x+a)+b]=5
∴(x+a)2﹣b2=5,
∴(x+a)2=5+b2
直接开平方整理得:x1=c;x2=d
上述过程中的a= 5 ;b= 2 ;c= ﹣2 ;d= ﹣8 .
(2)请用“平均数法”解方程:(x﹣5)(x+3)=6.
【解答】解:(1)原方程可变形为[(x+5)﹣2][(x+5)+2]=5,
∴(x+5)2﹣22=5,
∴(x+5)2=9,
∴直接开平方整理得:x1=﹣2;x2=﹣8,
∴a=5,b=2,c=﹣2,d=﹣8.
故答案为:5,2,﹣2,﹣8.
(2)(x﹣5)(x+3)=6,
原方程可变形为[(x﹣1)﹣4][(x﹣1)+4]=6,
∴(x﹣1)2﹣42=6,
∴(x﹣1)2=22,
∴直接开平方整理得:;
19.(2024秋 增城区校级月考)为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2018年市政府共投资4亿元人民币建设了廉租房,2020年计划投资9亿元人民币建设廉租房,若每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)请问2021年建设廉租房投资多少亿?
【解答】解:(1)设每年市政府投资的增长率为x,
根据题意,得:4(1+x)2=9,
解得x1=0.5=50%,x2=﹣3.5(舍去),
答:每年市政府投资的增长率为50%;
(2)2021年建设廉租房投资9(1+50%)=13.5(亿元),
所以2021年建设廉租房投资13.5亿元,
答:2021年建设廉租房投资13.5亿元.
20.(2024秋 海州区校级月考)如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1cm2?
【解答】解:(1)设经过x秒,使△PBQ的面积等于8cm2,
则AP=x cm,BQ=2x cm,
∴BP=AB﹣AP=(6﹣x)cm,
∵∠B=90°,
∴,
即,
解得:x=2或x=4,
答:经过2秒或4秒,使△PBQ的面积等于8cm2;
(2)①点P在线段AB上,点Q在线段BC中,
设经过y秒,△PBQ的面积为1cm2,0<y≤4,
依题意得:AP=y cm,CQ=2y cm,
∵AB=6cm,BC=8cm,
∴PB=(6﹣y)cm,BQ=(8﹣2y)cm,
由题意得:,
即,
解得:(舍去)或,
故符合题意;
②点P在线段AB上,点Q在CB的延长线上,
设经过m秒,△PBQ的面积为1cm2,4<m≤6,
依题意得:AP=m cm,CQ=2m cm,
∵AB=6cm,BC=8cm,
∴PB=(6﹣m)cm,BQ=(2m﹣8)cm,
由题意得:,
即,
解得:m=5(符合题意);
③点P在AB延长线上,点Q在CB的延长线上,
设经过n秒,△PBQ的面积为1cm2,n>6,
依题意得:AP=n cm,CQ=2n cm,
∵AB=6cm,BC=8cm,
∴PB=(n﹣6)cm,BQ=(2n﹣8)cm,
由题意得:,即,
解得:或(舍去),
故(符合题意);
答:经过秒或5秒或秒后△PBQ的面积为1cm2.
一.选择题(共6小题)
1.(2023秋 龙泉驿区期末)下列方程中,属于一元二次方程的是( )
A.x﹣2y=1 B. C.x2﹣2y+4=0 D.x2﹣2x+1=0
2.(2024秋 东城区校级月考)关于x的一元二次方程2x2+bx﹣1=0的根的情况是( )
A.实数根的个数由b的值确定
B.有两个不相等的实数根
C.有两个相等的实数根
D.没有实数根
3.(2023秋 旌阳区期末)若一元二次方程ax2+bx+c=0(a≠0)的一个根是x=1,则a+b+c的值是( )
A.0 B.﹣1 C.1 D.不能确定
4.(2024春 鹿城区校级期中)王老师购买了2304张签名卡,在毕业典礼上,他向每位同学赠送了一张签名卡,每位同学间也互赠了一张签名卡,签名卡恰好用完,设班级有x名学生,则下列方程成立的是( )
A. B.
C.x(x﹣1)+x=2304 D.x(x﹣1)=2304
5.(2024秋 裕华区校级月考)嘉嘉和琪琪一起写作业,在解一道一元二次方程时,嘉嘉在化简过程中写错了常数项,因而得到方程的两个根是﹣1和﹣5;琪琪在化简过程中写错了一次项的系数,因而得到方程的两个根是3和2.则正确的方程是( )
A.x2+6x+5=0 B.x2﹣5x+6=0 C.x2﹣5x+5=0 D.x2+6x+6=0
6.(2024秋 阿荣旗校级月考)如图,在长70m,宽40m的长方形花园中,欲修宽度相等的观赏路(如阴影部分所示),要使观赏路面积占总面积的,若设路宽为x m,则x应满足的方程是( )
A.(40﹣x)(70﹣x)=350
B.(40﹣2x)(70﹣3x)=2450
C.(40﹣2x)(70﹣3x)=350
D.(40﹣x)(70﹣x)=2150
二.填空题(共8小题)
7.(2023秋 宣汉县期末)已知关于x的方程(a+1)x2﹣2x+3=0有实数根,则整数a的最大值是 .
8.(2024 常州二模)已知m为方程x2﹣3x﹣6=0的一个根,则代数式﹣m2+3m﹣6的值是 .
9.(2024秋 建邺区校级期中)若关于x的一元二次方程ax2+bx+c=0(a、b、c都为有理数)的一个解是x1=4﹣2,则方程的另一个解是 .
10.(2024秋 东昌府区校级月考)参加会议的人两两彼此握手,一共握了55次手,那么一共有 人参加会议.
11.(2024秋 永寿县校级月考)一元二次方程(x﹣1)2=x+2的一般形式为 .(二次项的系数为正数)
12.(2024秋 即墨区校级月考)如图,王师傅要建一个矩形羊圈,羊圈的一边利用长为18m的住房墙,另外三边用45m长的彩钢围成,为了方便进出,在垂直于住房墙的一边要留出1m安装木门.若要使羊圈的面积为224m2,则所围矩形与墙垂直的一边长为 .
13.(2024秋 临湘市校级月考)《田亩比类乘除捷法》中记载了一道题:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步.”译文:一个矩形的面积为864平方步,宽比长少12步,问宽和长各多少步?设矩形的宽为x步,由题意,可列方程为 .
14.(2024秋 裕华区校级月考)若关于x的一元二次方程(m+4)x2﹣4x+1=0有两个不相等的实数根,则m的取值范围是 .
三.解答题(共6小题)
15.(2024秋 榆次区校级月考)解下列方程:
(1)(2x+5)(x﹣6)=0;
(2)2x2﹣4x﹣3=0;
(3)(2x+3)2=(3x+2)2;
(4)3y2﹣6y﹣5=0(用配方法求解).
16.(2024秋 双峰县月考)已知一元二次方程ax2+bx+c=0(a≠0).
(1)如果方程有一个根是1,那么a、b、c之间有什么关系?
(2)如果方程有一个根是﹣1,那么a、b、c之间有什么关系?
(3)如果方程有一个根是0,那么方程的系数或常数项有什么特征?
17.(2024秋 兴庆区校级月考)关于x的一元二次方程x2﹣3x+2=0.
(1)试判断该方程根的情况;
(2)若a,b是该方程的两个实数根,化简并求下面式子的值:.
18.(2024秋 德州月考)小明在解一元二次方程时,发现这样一种解法.
如:解方程x(x+4)=6
解:原方程可变形为[(x+2)﹣2][(x+2)+2]=6
∴(x+2)2﹣22=6,
∴(x+2)2=10
直接开平方整理得:;
我们称小明的这种解法为“平均数法”
(1)下面是小明用“平均数法”解方程(x+3)(x+7)=5时写的解题过程.
解:原方程变形为[(x+a)﹣b][(x+a)+b]=5
∴(x+a)2﹣b2=5,
∴(x+a)2=5+b2
直接开平方整理得:x1=c;x2=d
上述过程中的a= ;b= ;c= ;d= .
(2)请用“平均数法”解方程:(x﹣5)(x+3)=6.
19.(2024秋 增城区校级月考)为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2018年市政府共投资4亿元人民币建设了廉租房,2020年计划投资9亿元人民币建设廉租房,若每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)请问2021年建设廉租房投资多少亿?
20.(2024秋 海州区校级月考)如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1cm2?
第21章一元二次方程检测卷-2024-2025学年数学九年级上册人教版
参考答案与试题解析
一.选择题(共6小题)
1.(2023秋 龙泉驿区期末)下列方程中,属于一元二次方程的是( )
A.x﹣2y=1 B. C.x2﹣2y+4=0 D.x2﹣2x+1=0
【解答】解:A.方程x﹣2y=1是二元一次方程,选项A不符合题意;
B.方程x2+3=是分式方程,选项B不符合题意;
C.方程x2﹣2y+4=0是二元二次方程,选项C不符合题意;
D.方程x2﹣2x+1=0是一元二次方程,选项D符合题意.
故选:D.
2.(2024秋 东城区校级月考)关于x的一元二次方程2x2+bx﹣1=0的根的情况是( )
A.实数根的个数由b的值确定
B.有两个不相等的实数根
C.有两个相等的实数根
D.没有实数根
【解答】解:由题知,
Δ=b2﹣4×2×(﹣1)=b2+8≥8>0,
所以此一元二次方程有两个不相等的实数根.
故选:B.
3.(2023秋 旌阳区期末)若一元二次方程ax2+bx+c=0(a≠0)的一个根是x=1,则a+b+c的值是( )
A.0 B.﹣1 C.1 D.不能确定
【解答】解:把x=1代入方程得:a+b+c=0,
故选:A.
4.(2024春 鹿城区校级期中)王老师购买了2304张签名卡,在毕业典礼上,他向每位同学赠送了一张签名卡,每位同学间也互赠了一张签名卡,签名卡恰好用完,设班级有x名学生,则下列方程成立的是( )
A. B.
C.x(x﹣1)+x=2304 D.x(x﹣1)=2304
【解答】解:根据题意,王老师共赠送了x张签名卡,同学之间共赠送了x(x﹣1)张签名卡,
∴x(x﹣1)+x=2304;
故选:C.
5.(2024秋 裕华区校级月考)嘉嘉和琪琪一起写作业,在解一道一元二次方程时,嘉嘉在化简过程中写错了常数项,因而得到方程的两个根是﹣1和﹣5;琪琪在化简过程中写错了一次项的系数,因而得到方程的两个根是3和2.则正确的方程是( )
A.x2+6x+5=0 B.x2﹣5x+6=0 C.x2﹣5x+5=0 D.x2+6x+6=0
【解答】解:∵嘉嘉在化简过程中写错了常数项,因而得到方程的两个根是﹣1和﹣5,
∴两根之和﹣=﹣1+(﹣5)=﹣6,
∴当a=1时,b=6;
∵琪琪在化简过程中写错了一次项的系数,因而得到方程的两个根是3和2,
∴两根之积=﹣1×(﹣5)=5,
∴当a=1时,c=5,
∴正确的方程是x2+6x+5=0.
故选:A.
6.(2024秋 阿荣旗校级月考)如图,在长70m,宽40m的长方形花园中,欲修宽度相等的观赏路(如阴影部分所示),要使观赏路面积占总面积的,若设路宽为x m,则x应满足的方程是( )
A.(40﹣x)(70﹣x)=350
B.(40﹣2x)(70﹣3x)=2450
C.(40﹣2x)(70﹣3x)=350
D.(40﹣x)(70﹣x)=2150
【解答】解:∵设路宽为x m,所剩下的观赏面积的宽为(40﹣2x)m,长为(70﹣3x)m,要使观赏路面积占总面积,
∴,
即(40﹣2x)(70﹣3x)=2450.
故选:B.
二.填空题(共8小题)
7.(2023秋 宣汉县期末)已知关于x的方程(a+1)x2﹣2x+3=0有实数根,则整数a的最大值是 ﹣1 .
【解答】解:当a+1=0时,原方程为﹣2x+3=0,解得x=,
∴a=﹣1符合题意;
当a+1≠0时,Δ=(﹣2)2﹣4×(a+1)×3≥0,
解得:a≤﹣,
∴a≤﹣且a≠﹣1.
综上所述,a≤﹣.
又∵a为整数,
∴a的最大值为﹣1.
故答案为:﹣1.
8.(2024 常州二模)已知m为方程x2﹣3x﹣6=0的一个根,则代数式﹣m2+3m﹣6的值是 ﹣12 .
【解答】解:∵m为方程x2﹣3x﹣6=0的一个根,
∴m2﹣3m=6,
∴﹣m2+3m﹣6=﹣(m2﹣3m)﹣6=﹣6﹣6=﹣12.
故答案为:﹣12.
9.(2024秋 建邺区校级期中)若关于x的一元二次方程ax2+bx+c=0(a、b、c都为有理数)的一个解是x1=4﹣2,则方程的另一个解是 .
【解答】解:设方程的另一个根为x2,
∵关于x的一元二次方程ax2+bx+c=0中,a、b、c是有理数,
∴、都是有理数,
∴x1+x2,x1 x2均是有理数,
∵方程的一个根是,
∴方程的另一个根是,
故答案为:.
10.(2024秋 东昌府区校级月考)参加会议的人两两彼此握手,一共握了55次手,那么一共有 11 人参加会议.
【解答】解:设一共有x人参加会议,
则x(x﹣1)=55,
解得x1=11,x2=﹣10(不合题意舍去);
答:一共有11人.
故答案为:11.
11.(2024秋 永寿县校级月考)一元二次方程(x﹣1)2=x+2的一般形式为 x2﹣3x﹣1=0 .(二次项的系数为正数)
【解答】解:∵(x﹣1)2=x+2,
∴x2﹣2x+1=x+2,
∴x2﹣2x+1﹣x﹣2=0,
∴x2﹣3x﹣1=0,
∴一元二次方程(x﹣1)2=x+2的一般形式为x2﹣3x﹣1=0.
故答案为:x2﹣3x﹣1=0.
12.(2024秋 即墨区校级月考)如图,王师傅要建一个矩形羊圈,羊圈的一边利用长为18m的住房墙,另外三边用45m长的彩钢围成,为了方便进出,在垂直于住房墙的一边要留出1m安装木门.若要使羊圈的面积为224m2,则所围矩形与墙垂直的一边长为 16m .
【解答】解:设所围矩形与墙垂直的一边长为x m,
根据题意,得x(45+1﹣2x)=224,
解得x1=7,x2=16,
当x=7时,45+1﹣2x=32>18,不符题意,舍去,
当x=16时,45+1﹣2x=14<18,符合题意,
∴所围矩形与墙垂直的一边长为16m,
故答案为:16m.
13.(2024秋 临湘市校级月考)《田亩比类乘除捷法》中记载了一道题:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步.”译文:一个矩形的面积为864平方步,宽比长少12步,问宽和长各多少步?设矩形的宽为x步,由题意,可列方程为 x(x+12)=864 .
【解答】解:∵矩形的宽为x步,且宽比长少12步,
∴矩形的长为(x+12)步.
依题意,得:x(x+12)=864.
故答案为:x(x+12)=864.
14.(2024秋 裕华区校级月考)若关于x的一元二次方程(m+4)x2﹣4x+1=0有两个不相等的实数根,则m的取值范围是 m<0且m≠﹣4 .
【解答】解:∵关于x的一元二次方程(m+4)x2﹣4x+1=0有两个不相等的实数根,
∴Δ>0且m+4≠0,即(﹣4)2﹣4(m+4)>0且m≠﹣4,
解得m<0且m≠﹣4,
故答案为:m<0且m≠﹣4.
三.解答题(共6小题)
15.(2024秋 榆次区校级月考)解下列方程:
(1)(2x+5)(x﹣6)=0;
(2)2x2﹣4x﹣3=0;
(3)(2x+3)2=(3x+2)2;
(4)3y2﹣6y﹣5=0(用配方法求解).
【解答】解:(1)由题意得2x+5=0或x﹣6=0,
∴,x2=6;
(2)∵a=2,b=﹣4,c=﹣3,
∴Δ=(﹣4)2﹣4×2×(﹣3)=40>0,
∴,
∴,;
(3)开方得2x+3=±(3x+2),
即2x+3=3x+2或2x+3=﹣(3x+2),
∴x1=1,x2=﹣1;
(4)∵3y2﹣6y﹣5=0,
∴,
∴,
∴,
即,
∴,
∴,.
16.(2024秋 双峰县月考)已知一元二次方程ax2+bx+c=0(a≠0).
(1)如果方程有一个根是1,那么a、b、c之间有什么关系?
(2)如果方程有一个根是﹣1,那么a、b、c之间有什么关系?
(3)如果方程有一个根是0,那么方程的系数或常数项有什么特征?
【解答】解:(1)将x=1代入原方程得:a×1+b×1+c=0,
即a+b+c=0;
(2)将x=﹣1代入原方程得:a×(﹣1)2+b×(﹣1)+c=0,
即a﹣b+c=0;
(3)将x=0代入原方程可得:a×0+b×0+c=0,
∴c=0.
17.(2024秋 兴庆区校级月考)关于x的一元二次方程x2﹣3x+2=0.
(1)试判断该方程根的情况;
(2)若a,b是该方程的两个实数根,化简并求下面式子的值:.
【解答】解:(1)∵Δ=(﹣3)2﹣4×2×1=1>0,
∴方程有两个不相等的实数根;
(2)∵a,b是该方程的两个实数根,
∴a+b=3,ab=2,
=
=
=
=
=
=
=;
∵a+b=3,
∴原式=.
18.(2024秋 德州月考)小明在解一元二次方程时,发现这样一种解法.
如:解方程x(x+4)=6
解:原方程可变形为[(x+2)﹣2][(x+2)+2]=6
∴(x+2)2﹣22=6,
∴(x+2)2=10
直接开平方整理得:;
我们称小明的这种解法为“平均数法”
(1)下面是小明用“平均数法”解方程(x+3)(x+7)=5时写的解题过程.
解:原方程变形为[(x+a)﹣b][(x+a)+b]=5
∴(x+a)2﹣b2=5,
∴(x+a)2=5+b2
直接开平方整理得:x1=c;x2=d
上述过程中的a= 5 ;b= 2 ;c= ﹣2 ;d= ﹣8 .
(2)请用“平均数法”解方程:(x﹣5)(x+3)=6.
【解答】解:(1)原方程可变形为[(x+5)﹣2][(x+5)+2]=5,
∴(x+5)2﹣22=5,
∴(x+5)2=9,
∴直接开平方整理得:x1=﹣2;x2=﹣8,
∴a=5,b=2,c=﹣2,d=﹣8.
故答案为:5,2,﹣2,﹣8.
(2)(x﹣5)(x+3)=6,
原方程可变形为[(x﹣1)﹣4][(x﹣1)+4]=6,
∴(x﹣1)2﹣42=6,
∴(x﹣1)2=22,
∴直接开平方整理得:;
19.(2024秋 增城区校级月考)为落实国务院房地产调控政策,使“居者有其屋”,某市加快了廉租房的建设力度.2018年市政府共投资4亿元人民币建设了廉租房,2020年计划投资9亿元人民币建设廉租房,若每年投资的增长率相同.
(1)求每年市政府投资的增长率;
(2)请问2021年建设廉租房投资多少亿?
【解答】解:(1)设每年市政府投资的增长率为x,
根据题意,得:4(1+x)2=9,
解得x1=0.5=50%,x2=﹣3.5(舍去),
答:每年市政府投资的增长率为50%;
(2)2021年建设廉租房投资9(1+50%)=13.5(亿元),
所以2021年建设廉租房投资13.5亿元,
答:2021年建设廉租房投资13.5亿元.
20.(2024秋 海州区校级月考)如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1cm2?
【解答】解:(1)设经过x秒,使△PBQ的面积等于8cm2,
则AP=x cm,BQ=2x cm,
∴BP=AB﹣AP=(6﹣x)cm,
∵∠B=90°,
∴,
即,
解得:x=2或x=4,
答:经过2秒或4秒,使△PBQ的面积等于8cm2;
(2)①点P在线段AB上,点Q在线段BC中,
设经过y秒,△PBQ的面积为1cm2,0<y≤4,
依题意得:AP=y cm,CQ=2y cm,
∵AB=6cm,BC=8cm,
∴PB=(6﹣y)cm,BQ=(8﹣2y)cm,
由题意得:,
即,
解得:(舍去)或,
故符合题意;
②点P在线段AB上,点Q在CB的延长线上,
设经过m秒,△PBQ的面积为1cm2,4<m≤6,
依题意得:AP=m cm,CQ=2m cm,
∵AB=6cm,BC=8cm,
∴PB=(6﹣m)cm,BQ=(2m﹣8)cm,
由题意得:,
即,
解得:m=5(符合题意);
③点P在AB延长线上,点Q在CB的延长线上,
设经过n秒,△PBQ的面积为1cm2,n>6,
依题意得:AP=n cm,CQ=2n cm,
∵AB=6cm,BC=8cm,
∴PB=(n﹣6)cm,BQ=(2n﹣8)cm,
由题意得:,即,
解得:或(舍去),
故(符合题意);
答:经过秒或5秒或秒后△PBQ的面积为1cm2.
同课章节目录
