2024-2025学年人教版数学八年级上册期中模拟试题(第十一章-第十三章)(含答案)
文档属性
| 名称 | 2024-2025学年人教版数学八年级上册期中模拟试题(第十一章-第十三章)(含答案) | 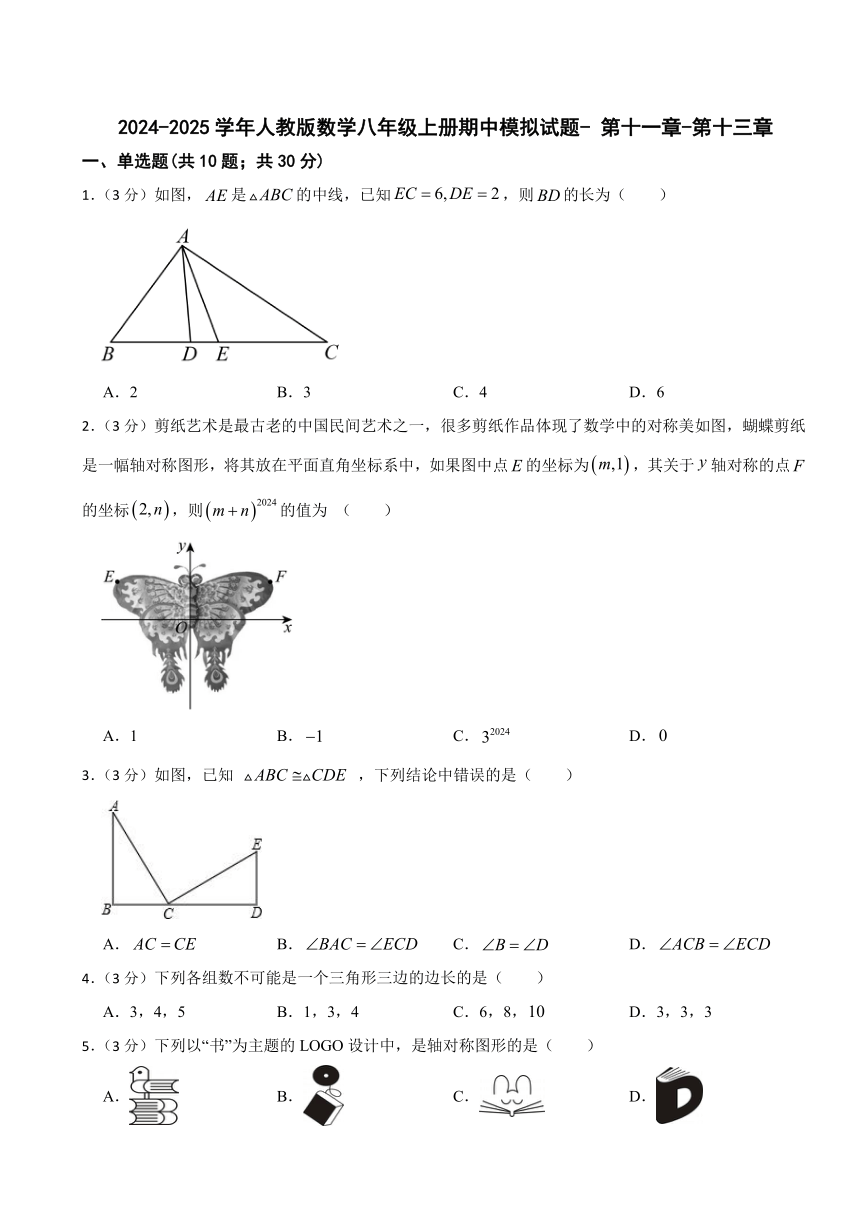 | |
| 格式 | docx | ||
| 文件大小 | 513.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-02 18:10:35 | ||
图片预览



文档简介
2024-2025学年人教版数学八年级上册期中模拟试题- 第十一章-第十三章
一、单选题(共10题;共30分)
1.(3分)如图,是的中线,已知,则的长为( )
A.2 B.3 C.4 D.6
2.(3分)剪纸艺术是最古老的中国民间艺术之一,很多剪纸作品体现了数学中的对称美如图,蝴蝶剪纸是一幅轴对称图形,将其放在平面直角坐标系中,如果图中点的坐标为,其关于轴对称的点的坐标,则的值为 ( )
A.1 B. C. D.
3.(3分)如图,已知 ,下列结论中错误的是( )
A. B. C. D.
4.(3分)下列各组数不可能是一个三角形三边的边长的是( )
A.3,4,5 B.1,3,4 C.6,8, D.3,3,3
5.(3分)下列以“书”为主题的LOGO设计中,是轴对称图形的是( )
A. B. C. D.
6.(3分)如图,△ABC中,AB=AC,∠B=70°,则∠A的度数是( )
A.70° B.55° C.50° D.40°
7.(3分)已知n边形的每个内角都相等,则使得n边形的每个内角的度数都是整数的n的值有( )
A.18个 B.20个 C.22个 D.无数个
8.(3分)如图,点A、B、C在一条直线上,和均为正三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①;②;③;④;⑤AE与DB所夹锐角为60°.其中正确的有(
A.5个 B.4个 C.3个 D.2个
9.(3分)如图, ,点 、 、 …在射线 上,点 、 、 …在射线 上, 、 、 …均为等边三角形,依此类推,若 ,则 的边长为( )
A. B. C.2016 D.4032
10.(3分)如图,在锐角三角形中,是边上的高,分别以为一边,向外作正方形和(正方形四条边都相等,四个角都是直角),连接和与的延长线交于点,下列结论:①;②;③是的中线;④.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共6题;共21分)
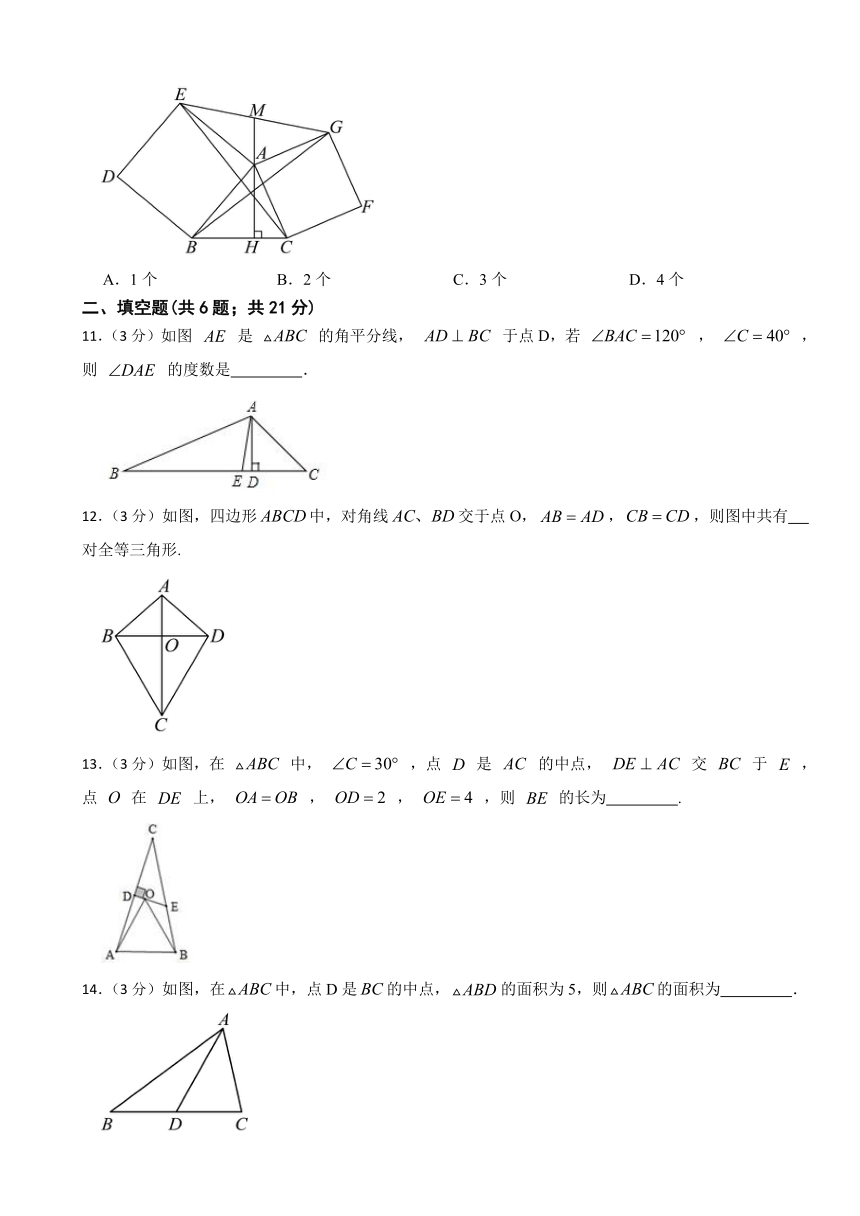
11.(3分)如图 是 的角平分线, 于点D,若 , ,则 的度数是 .
12.(3分)如图,四边形中,对角线交于点O,,,则图中共有 对全等三角形.
13.(3分)如图,在 中, ,点 是 的中点, 交 于 ,点 在 上, , , ,则 的长为 .
14.(3分)如图,在中,点D是的中点,的面积为5,则的面积为 .
15.(3分)如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD= .
16.(6分)若三边均不相等的三角形三边a,b,c满足(a为最长边,c为最短边),则称它为“不均衡三角形”.例如,一个三角形三边分别为7,5,4,因为,所以这个三角形为“不均衡三角形”.
(1)以下两组长度的小木棚能组成“不均衡三角形”的为 (填序号).
①,,; ②,,.
(2)已知“不均衡三角形”三边分别为,16,直接写出x的整数值为 .
三、解答题(共6题;共49分)
17.(7分)如图,在中,为边上的高,点D为边上的一点,连接.
(1)(3分)当为边上的中线时,若,的面积为24,求的长;
(2)(4分)当为的角平分线时,
①若,求的度数;
②若,则 .
18.(7分)如图,六边形的每个内角都相等,且,求的度数.
19.(8分)如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上.
(1)若BE⊥AD,∠F=62°,求∠A的大小.
(2)若AD=9cm,BC=5cm,求AB的长.
20.(8分)请认真完成下列的数学活动
我们知道,三角形的一个外角等于与它不相邻的两个内角的和,那么三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
●尝试探究(1)如图①,与分别为的两个外角,试探究与之间的数量关系.
●初步运用(2)如图②,在纸片中前去,得到四边形.若,则___________.小明联想到了曾经解决的一个问题:如图③,在中,,分别平分外角,,则与之间的数量关系为________________(请利用上面的结论直接写出答案).
●拓展提升(3)如图④,在四边形中,,分别平分外角,,设.
①试说明与的数量关系;
②根据值的情况,请直接判断的形状(按角分类).
21.(9分)如图,若 和 都是等边三角形,求 的度数.
22.(10分)如图,在四边形ABCD中,,,,点E是线段BD上一点,且.
(1)(5分)求证:;
(2)(5分)直接写出图中所有的等腰三角形.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】A
9.【答案】A
10.【答案】D
11.【答案】10°
12.【答案】3
13.【答案】8
14.【答案】10
15.【答案】1
16.【答案】①;或或或
17.【答案】(1);
(2)①的度数为;②
18.【答案】
19.【答案】(1)∠A=28°;(2)AB =2 cm.
20.【答案】(1)
(2);
(3)①;②当时,为钝角三角形;当,为直角三角形;当时,为锐角三角形
21.【答案】证明:∵△ABD、△AEC都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠CAE=60°,
∵∠DAC=∠BAC+60°,∠BAE=∠BAC+60°,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴∠ABE=∠ADC
设AB与CD交于点F,
∵∠BFO=∠DFA
∴∠BOF=180°-∠ABE-∠BFO=180°-∠ADC-∠DFA=∠DAB=60°
∴∠BOC=180°-∠BOF=120°.
22.【答案】(1)证明:∵∴,∵,∴,在和中,
∴
(2)解:、是等腰三角形
一、单选题(共10题;共30分)
1.(3分)如图,是的中线,已知,则的长为( )
A.2 B.3 C.4 D.6
2.(3分)剪纸艺术是最古老的中国民间艺术之一,很多剪纸作品体现了数学中的对称美如图,蝴蝶剪纸是一幅轴对称图形,将其放在平面直角坐标系中,如果图中点的坐标为,其关于轴对称的点的坐标,则的值为 ( )
A.1 B. C. D.
3.(3分)如图,已知 ,下列结论中错误的是( )
A. B. C. D.
4.(3分)下列各组数不可能是一个三角形三边的边长的是( )
A.3,4,5 B.1,3,4 C.6,8, D.3,3,3
5.(3分)下列以“书”为主题的LOGO设计中,是轴对称图形的是( )
A. B. C. D.
6.(3分)如图,△ABC中,AB=AC,∠B=70°,则∠A的度数是( )
A.70° B.55° C.50° D.40°
7.(3分)已知n边形的每个内角都相等,则使得n边形的每个内角的度数都是整数的n的值有( )
A.18个 B.20个 C.22个 D.无数个
8.(3分)如图,点A、B、C在一条直线上,和均为正三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①;②;③;④;⑤AE与DB所夹锐角为60°.其中正确的有(
A.5个 B.4个 C.3个 D.2个
9.(3分)如图, ,点 、 、 …在射线 上,点 、 、 …在射线 上, 、 、 …均为等边三角形,依此类推,若 ,则 的边长为( )
A. B. C.2016 D.4032
10.(3分)如图,在锐角三角形中,是边上的高,分别以为一边,向外作正方形和(正方形四条边都相等,四个角都是直角),连接和与的延长线交于点,下列结论:①;②;③是的中线;④.其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共6题;共21分)
11.(3分)如图 是 的角平分线, 于点D,若 , ,则 的度数是 .
12.(3分)如图,四边形中,对角线交于点O,,,则图中共有 对全等三角形.
13.(3分)如图,在 中, ,点 是 的中点, 交 于 ,点 在 上, , , ,则 的长为 .
14.(3分)如图,在中,点D是的中点,的面积为5,则的面积为 .
15.(3分)如图,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB,若AB=4,CF=3,则BD= .
16.(6分)若三边均不相等的三角形三边a,b,c满足(a为最长边,c为最短边),则称它为“不均衡三角形”.例如,一个三角形三边分别为7,5,4,因为,所以这个三角形为“不均衡三角形”.
(1)以下两组长度的小木棚能组成“不均衡三角形”的为 (填序号).
①,,; ②,,.
(2)已知“不均衡三角形”三边分别为,16,直接写出x的整数值为 .
三、解答题(共6题;共49分)
17.(7分)如图,在中,为边上的高,点D为边上的一点,连接.
(1)(3分)当为边上的中线时,若,的面积为24,求的长;
(2)(4分)当为的角平分线时,
①若,求的度数;
②若,则 .
18.(7分)如图,六边形的每个内角都相等,且,求的度数.
19.(8分)如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上.
(1)若BE⊥AD,∠F=62°,求∠A的大小.
(2)若AD=9cm,BC=5cm,求AB的长.
20.(8分)请认真完成下列的数学活动
我们知道,三角形的一个外角等于与它不相邻的两个内角的和,那么三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
●尝试探究(1)如图①,与分别为的两个外角,试探究与之间的数量关系.
●初步运用(2)如图②,在纸片中前去,得到四边形.若,则___________.小明联想到了曾经解决的一个问题:如图③,在中,,分别平分外角,,则与之间的数量关系为________________(请利用上面的结论直接写出答案).
●拓展提升(3)如图④,在四边形中,,分别平分外角,,设.
①试说明与的数量关系;
②根据值的情况,请直接判断的形状(按角分类).
21.(9分)如图,若 和 都是等边三角形,求 的度数.
22.(10分)如图,在四边形ABCD中,,,,点E是线段BD上一点,且.
(1)(5分)求证:;
(2)(5分)直接写出图中所有的等腰三角形.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】A
9.【答案】A
10.【答案】D
11.【答案】10°
12.【答案】3
13.【答案】8
14.【答案】10
15.【答案】1
16.【答案】①;或或或
17.【答案】(1);
(2)①的度数为;②
18.【答案】
19.【答案】(1)∠A=28°;(2)AB =2 cm.
20.【答案】(1)
(2);
(3)①;②当时,为钝角三角形;当,为直角三角形;当时,为锐角三角形
21.【答案】证明:∵△ABD、△AEC都是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠CAE=60°,
∵∠DAC=∠BAC+60°,∠BAE=∠BAC+60°,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
,
∴△DAC≌△BAE(SAS),
∴∠ABE=∠ADC
设AB与CD交于点F,
∵∠BFO=∠DFA
∴∠BOF=180°-∠ABE-∠BFO=180°-∠ADC-∠DFA=∠DAB=60°
∴∠BOC=180°-∠BOF=120°.
22.【答案】(1)证明:∵∴,∵,∴,在和中,
∴
(2)解:、是等腰三角形
同课章节目录
