人教版 六年级数学上册 第三单元测试(含解析)
文档属性
| 名称 | 人教版 六年级数学上册 第三单元测试(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 443.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-02 17:53:38 | ||
图片预览



文档简介
六年级数学第三单元测试
一、选择题
1.小云小时走3千米,她每小时走( )千米。
A.4 B. C.3 D.
2.假分数的倒数( )1。
A.大于 B.小于 C.小于或等于
3.加工56个零件,甲单独做需要9小时,乙单独做需要15小时,求甲、乙合作需要几小时,正确的算式是( )。
A. B. C. D.56÷9+56÷15
4.一台榨油机小时榨油,求平均每小时榨油多少吨,正确的列式是( )。
A. B. C. D.
5.下面算式中,( )的商一定大于被除数。
A.÷1 B.÷6 C. D.
二、填空题
6.一根拔河比赛绳的是8m,这根绳子总长是( )m。
7.6和( )互为倒数,( )没有倒数。
8.在括号里填上“>”“<”或“=”。
( ) ( ) ( )
9.一个数的是60,这个数的是( );比的倒数多3的数是( )。
10.×( )=0.8×( )=( )×29=1
11.小明小时走km。照这样计算,他1小时能走( )km,走1km用( )小时。
12.( )千米相当于12千米的,吨是( )吨的。
13.小红骑自行车分钟行千米,她骑自行车每分钟行( )千米,行1千米需要( )分钟。
14.一根彩带长米,用去米,还剩( )米。另一根彩带用去它的,正好是米。这根彩带长( )米。
15.客车和货车同时从A地、B地相对开出,客车每小时行60千米,货车每小时行全程的,当货车行到全程的时,客车已行全程的,则A、B两地间的路程是( )千米。
三、判断题
16.如果A与B的乘积是1,那么A与B互为倒数。( )
17.任何真分数的倒数都是假分数。( )
18.一根木料用去了米,还剩这根木料的,用去的和剩下的同样长。( )
19.男生人数比女生人数多,那么女生人数比男生人数少。( )
20.新光小学四月份用水120吨,比五月份节约了,正好节约了30吨。( )
四、计算题
21.直接写得数。
×= 0÷= ÷3=
÷= ×= 12÷=
22.计算。(能简算的要简算)
×+÷
÷(+) 23-
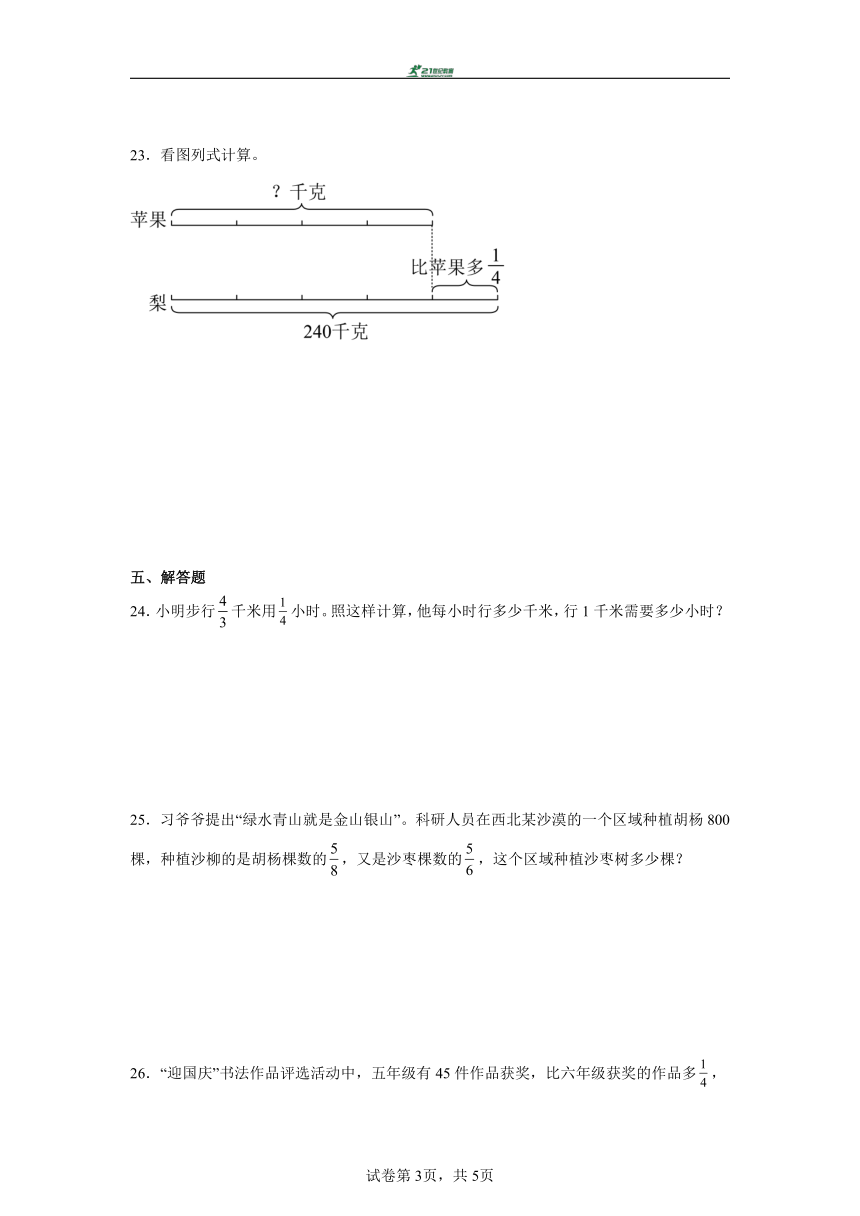
23.看图列式计算。
五、解答题
24.小明步行千米用小时。照这样计算,他每小时行多少千米,行1千米需要多少小时?
25.习爷爷提出“绿水青山就是金山银山”。科研人员在西北某沙漠的一个区域种植胡杨800棵,种植沙柳的是胡杨棵数的,又是沙枣棵数的,这个区域种植沙枣树多少棵?
26.“迎国庆”书法作品评选活动中,五年级有45件作品获奖,比六年级获奖的作品多,六年级有多少件作品获奖?
27.淘气看一本科普书,第一天看了全书的25%,第二天看了剩下的。
(1)两天正好看了130页,这本书有多少页?
(2)第一天比第二天多看了10页,这本书有多少页?
28.用汽车将一批物资运往灾区,第一次运走总数的,第二次运走余下的,这时还剩下24吨。这批物资一共有多少吨?
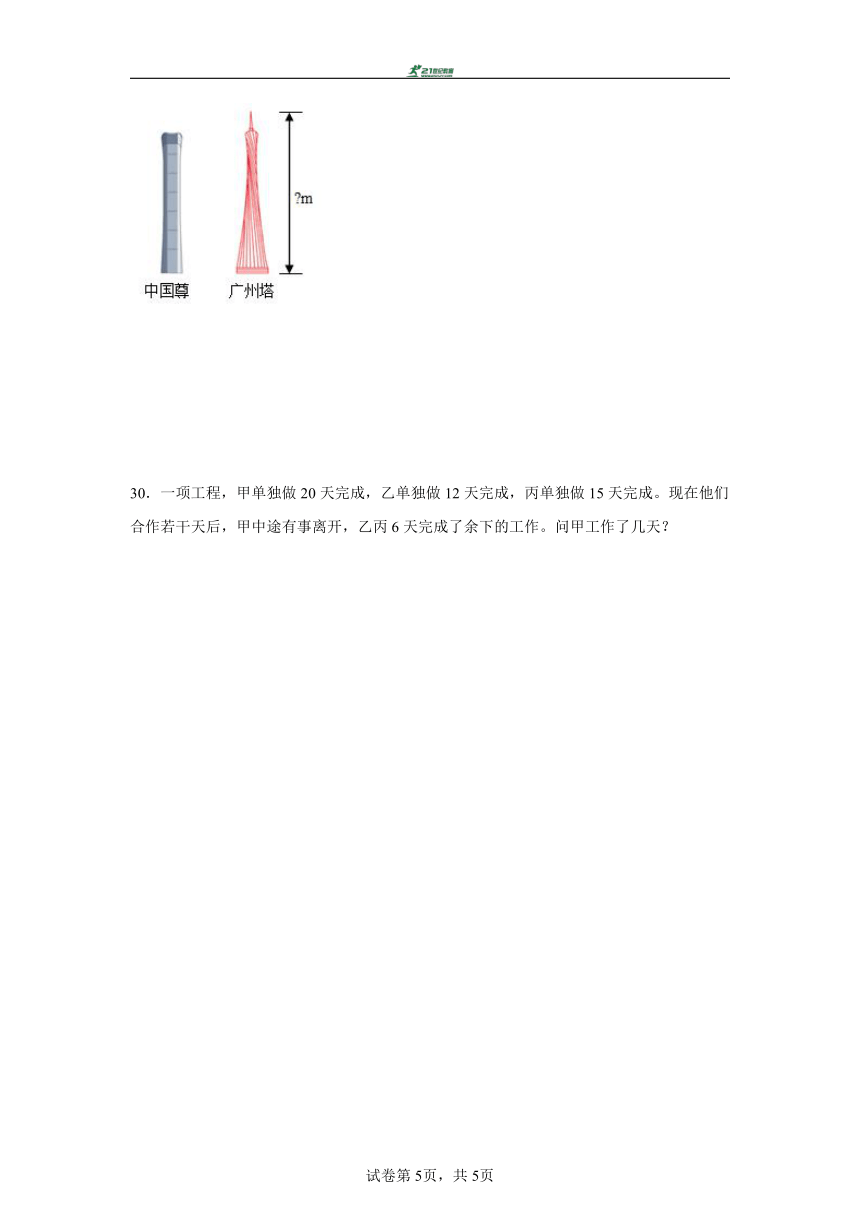
29.中国尊是北京一处地标性建筑,它的外形是仿照我国古代用来盛酒的器具“尊”进行设计的,高度为528m,比广州塔矮。广州塔的高度是多少米?
30.一项工程,甲单独做20天完成,乙单独做12天完成,丙单独做15天完成。现在他们合作若干天后,甲中途有事离开,乙丙6天完成了余下的工作。问甲工作了几天?
试卷第11页,共33页
试卷第11页,共33页
参考答案:
题号 1 2 3 4 5
答案 A C A B D
1.A
【分析】求每小时走多少千米,实际上是求小云的速度,根据路程÷时间=速度,代入数据即可得解。
【详解】3÷=3×=4(千米)
即她每小时走4千米。
故答案为:A
【点睛】此题主要根据路程、时间、速度三者之间的关系,利用分数除法的计算,求出结果。
2.C
【分析】根据倒数的意义,乘积是1的两个数互为倒数。因为假分数的分子等于或大于分母,把分子和分母调换位置后,则成了分子小于或等于分母,所以假分数的倒数小于或等于1。据此解答。
【详解】根据分析得,假分数的倒数小于或等于1。
故答案为:C
【点睛】此题考查的目的是理解倒数、假分数的意义,掌握求一个数的倒数的方法。
3.A
【分析】把加工56个零件的工作总量看作单位“1”,根据“工作效率=工作总量÷工作时间”,分别求出甲、乙各自的工作效率,甲、乙的工作效率相加即是合作工效;根据“合作工时=工作总量÷合作工效”,求出甲、乙合作需要的时间。
【详解】甲的工作效率:
乙的工作效率:
(小时)
甲、乙合作需要小时。
正确的算式是。
故答案为:A
4.B
【分析】用榨油总量除以榨油时间,求出平均每小时榨油多少吨,据此列式计算即可。
【详解】根据分析可知,平均每小时榨油:。
故答案为:B
5.D
【分析】一个非零的数如果除以一个大于1的数,商就小于被除数;如果除以一个小于1的数商就大于被除数;如果除以1商就等于被除数;据此解答。
【详解】A.÷1,除数等于1,÷1=;
B.÷6,除数大于1,÷6<;
C.,除数大于1,÷<;
D.,除数小于1,÷>;
故答案为:D
【点睛】本题主要考查了除法算式中,除数的变化,引起商和被除数之间的变化规律。
6.36
【分析】把这根绳子总长看作单位“1”,单位“1”未知,根据分数除法的意义,已知一个数的几分之几是多少,求这个数,用除法,用8除以,即可求出这根绳子的总长。
【详解】8÷=8×=36(m)
即这根绳子总长是36m。
【点睛】此题主要考查分数除法的应用,掌握已知一个数的几分之几是多少,求这个数的计算方法,从而解决问题。
7. 0
【分析】根据倒数的意义,乘积是1的两个数互为倒数,1的倒数是1,0没有倒数,据此解答。
【详解】因为6×=1,所以6和互为倒数;
0没有倒数。
【点睛】此题考查的目的是理解倒数的意义,掌握求倒数的方法及应用,明确:1的倒数是1,0没有倒数。
8. > < >
【分析】一个数(0除外)除以小于1的数,商大于这个数;一个数(0除外)除以大于1的数,商小于这个数;
一个数(0除外)乘小于1的数,积小于这个数;一个数(0除外)乘大于1的数,积大于这个数,据此解答即可。
【详解】>,<,所以>;
<;
>,<,所以>
【点睛】本题属于基础性题目,熟练掌握规律能够提高解答速度,也可以计算出来再比较。
9. 27 15
【分析】一个数的是60,据此可以求出这个数,进而求出这个数的;比的倒数多3的数,我们要先求出的倒数,然后再加上3,即可求出这个数。
【详解】第一空:60÷×
=60××
=27
第二空:的倒数是12
12+3=15
【点睛】本题考查分数乘除法的应用以及倒数的相关知识点。
10. 1.25/
【分析】观察式子,三个算式的乘积都是1,所以本题相当于填、0.8和29的倒数。据此解题。
【详解】×=0.8×1.25=×29=1
或×=0.8×=×29=1。
【点睛】本题考查了倒数的认识,乘积是1的两个数互为倒数,求分数的倒数,将分子分母调换位置即可。
11.
【分析】求平均每小时走多少km,就是求速度,速度=路程÷时间;求平均走1km用多少小时,用时间除以路程。
【详解】÷=(km)
÷=(小时)
【点睛】此题考查了行程问题,掌握分数除法的计算法则是解题关键。除以一个数等于乘这个数的倒数。
12. 9
【分析】把12千米看作单位“1”,求12千米的是多少千米,用乘法计算;把要求的吨数看作单位“1”,已知它的是吨,求这个数,用除法计算。
【详解】12×=9(米)
÷
=×
=(吨)
【点睛】本题考查分数乘、除法的意义及应用,明确求一个数的几分之几是多少,用乘法计算;已知一个数的几分之几是多少,求这个数,用除法计算。
13. 3
【分析】除以一个数等于乘这个数的倒数,第一个空,根据路程÷时间=速度,列式计算;第二个空,根据路程÷速度=时间,列式计算。
【详解】÷=×=(千米)
1÷=1×3=3(分钟)
小红骑自行车分钟行千米,她骑自行车每分钟行千米,行1千米需要3分钟。
14.
【分析】(1)剩下彩带的长度=彩带的总长度-用去部分彩带的长度;
(2)把这根彩带的总长度看作单位“1”,根据“量÷对应的分率”即可求得这根彩带的总长度;据此解答。
【详解】(1)-=(米)
(2)÷=(米)
【点睛】掌握异分母分数加减法的计算方法并找出米对应的分率是解答题目的关键。
15.520
【分析】已知货车每小时行全程的,货车行到全程的时,根据除法的意义,用÷即可求出货车行到全程的需要的时间,也就是小时,客车已行全程的也需要小时;再根据速度×时间=路程,用即可求出全程的是多少千米,也就是325千米,再把全程看作单位“1”,根据分数除法的意义,用即可求出全程。
【详解】
(小时)
(千米)
(千米)
A、B两地间的路程是520千米。
【点睛】本题主要考查了相遇问题,明确客车和货车行驶时间相同是解答本题的关键。
16.√
【分析】乘积是1的两个数互为倒数;据此判断。
【详解】如果A与B的乘积是1,那么A与B互为倒数。
原题说法正确。
故答案为:√
【点睛】本题考查倒数的意义及应用,注意倒数是对两个数而言,是两个数相互依存的一个概念。
17.√
【分析】真分数:分子小于分母的的分数;假分数:分子大于或等于分母的分数;根据求一个倒数的方法,是把一个分数的分子分母互换位置就得到这个分数的倒数,真分数的分子分母互换位置后就变成假分数,可以举例解答。
【详解】如:,的倒数是,是假分数。
任何真分数的倒数都是假分数。
原题干说法正确。
故答案为:√
18.×
【分析】由题意可知,一根木料用去了米,还剩这根木料的,则用去了这根木料的1-=,根据分数除法的意义,可求出这根木料的长度,进而判断即可。
【详解】÷(1-)
=÷
=(米)
-=(米)
则还剩下米,故原题干说法错误。
【点睛】本题考查分数除法,明确分数除法的计算方法是解题的关键。
19.×
【分析】把女生人数看作单位“1”,则男生的人数为1×(1+);然后求出女生人数比男生人数少多少,再除以男生人数即可,据此判断。
【详解】假设女生的人数为1,男生人数为:
1×(1+)
=1×
=
(-1)÷
=÷
=×
=
则女生人数比男生人数少。原题干说法错误。
故答案为:×
【点睛】本题考查求一个数比另一个数少几分之几,明确用除法是解题的关键。
20.×
【分析】将五月份用水量看作单位“1”,未知,则四月份用水量是五月份的(1-),是120吨;用除法求出五月份的用水量,最后求四月份与五月份用水量的差即可。
【详解】120÷(1-)
=120÷
=160(吨)
160-120=40(吨)
所以四月份比五月份节约用水40吨。
故答案为:×
【点睛】本题主要考查“已知一个数的几分之几是多少,求这个数用除法”,找准120吨水对应的分率是解题的关键。
21.;0;
;;16
【解析】略
22.;7;;
;;5
【分析】(1)先把除法转化为乘法,再逆用乘法分配律简算。
(2)先利用乘法分配律去括号,再利用加法结合律简算。
(3)先把除法转化为乘法,再利用乘法交换律、乘法结合律简算。
(4)先算括号里面的,再算括号外面的。
(5)先算小括号里面的,再算中括号里面的,最后算中括号外面的。
(6)先把除法转化为乘法,再算乘法,最后算减法。
【详解】×+÷
=×+×
=(+)×
=1×
=
=
=
=
=6+1
=7
=
=
=
=
=
÷(+)
=÷(+)
=÷
=×
=
=
=
=
=
=
23-
=23-
=23-18
=5
23.192千克
【分析】线段图的意思是,梨有240千克,比苹果多,求苹果有多少千克?
把苹果的质量看作单位“1”,梨的质量比苹果多,则梨的质量是苹果的(1+),单位“1”未知用除法计算,即可求出苹果的质量。
【详解】240÷(1+)
=240÷
=240×
=192(千克)
苹果有192千克。
24.千米;小时
【分析】已知小明步行千米用小时,根据:速度=路程÷时间,用÷,即可求出每小时行驶多少千米;再用1千米除以速度,即可求出需要多少小时。
【详解】(千米)
(小时)
答:小明每小时行千米,行1千米需要小时。
25.600棵
【分析】把胡杨的棵数看作单位“1”,单位“1”已知,根据分数乘法的意义,用800乘求出沙柳的棵数,接着把沙枣的棵数看作单位“1”,单位“1”未知,根据分数除法的意义,用沙柳的棵数除以,即可求出沙枣树的棵数。
【详解】800×÷
=500÷
=600(棵)
答:这个区域种植沙枣树600棵。
【点睛】此题主要考查分数乘除法的意义,注意前后两个单位“1”的不同。
26.36件
【分析】已知五年级有45件作品获奖,比六年级获奖的作品多,可把六年级获奖作品数量看作单位“1”,则五年级获奖作品占六年级的(1+),根据已知一个数的几分之几是多少,求这个数用除法计算,要求得六年级有多少件作品获奖,可列式为:。
【详解】
=45÷
=45×
=36(件)
答:六年级有36件作品获奖。
【点睛】本题考查了分数除法的应用,需要先确定好单位“1”,再结合比较量占单位“1”的具体分率来列式计算。
27.(1)280页
(2)140页
【分析】(1)先把百分数换成分数,25%=,所以剩下了,第二天看了剩下的,即用×,算出第二天看了全书的几分之几,再用130除以第一天和第二天看的占比之和,即可算出书的总页数。
(2)根据题意可知,用13除以第一天和第二天看的占比之差,即可算出答案。
【详解】(1)第一天看的页数占比:25%=
第二天看的页数占比:×
=
=
总页数:
=
=
=
=280(页)
答:这本书一共有280页。
(2)
=
=
=10×14
=140(页)
答:这本书一共有140页。
【点睛】此题考查了学生的理解分析能力以及分数乘除法的运算。
28.48吨
【分析】把这批物资的总数看做单位“1”,第一次运走总数的,剩下总数的(1-);第二次运走余下的,即第二次运走总数的(1-)的,根据求一个数的几分之几是多少,用乘法计算,求出第二次运走总数的几分之几;
先根据减法的意义,用“1”分别减去第一次、第二次运走总数的分率,就是剩下的吨数占总数的几分之几,然后根据已知一个数的几分之几是多少,求这个数,用除法计算,即可求出这批物资的总数。
【详解】第二次运走总数的:
(1-)×
=×
=
总数:
24÷(1--)
=24÷
=24×2
=48(吨)
答:这批物资一共有48吨。
【点睛】本题考查分数乘除法的应用,找出单位“1”,关键是根据分数乘法的意义求出第二次运走总数的几分之几,然后根据分数除法的意义求出总数。
29.600米
【分析】把广州塔的高度看成单位“1”,它的(1-)是528米,根据分数除法的意义,用528除以(1-)即可求出广州塔的高度。
【详解】528÷(1-)
=528÷
=600(米)
答:广州塔的高度是600米。
【点睛】本题的关键是找出单位“1”,并找出数量对应了单位“1”的几分之几,再用除法就可以求出单位“1”的量。
30.天
【分析】把这项工程的量看作单位“1”,先依据工作总量÷工作时间=工作效率,求出甲、乙、丙的工作效率,乙丙6天完成了余下的工作,根据工作总量=工作时间×工作效率,求出乙丙6天完成的工作量,用1减去乙丙6天完成的工作量,求出三人完成的工作量,再根据工作时间=工作量÷三人工作效率和即可求出甲工作了几天。
【详解】1÷20=
1÷12=
1÷15=
1-6×(+)
=1-6×(+)
=1-6×
=1-
=
÷(++)
=÷(++)
=÷
=×
=(天)
答:甲工作了天。
【点睛】本题考查知识点:依据工作时间,工作效率以及工作总量之间数量关系解决问题。
答案第11页,共22页
答案第11页,共22页
一、选择题
1.小云小时走3千米,她每小时走( )千米。
A.4 B. C.3 D.
2.假分数的倒数( )1。
A.大于 B.小于 C.小于或等于
3.加工56个零件,甲单独做需要9小时,乙单独做需要15小时,求甲、乙合作需要几小时,正确的算式是( )。
A. B. C. D.56÷9+56÷15
4.一台榨油机小时榨油,求平均每小时榨油多少吨,正确的列式是( )。
A. B. C. D.
5.下面算式中,( )的商一定大于被除数。
A.÷1 B.÷6 C. D.
二、填空题
6.一根拔河比赛绳的是8m,这根绳子总长是( )m。
7.6和( )互为倒数,( )没有倒数。
8.在括号里填上“>”“<”或“=”。
( ) ( ) ( )
9.一个数的是60,这个数的是( );比的倒数多3的数是( )。
10.×( )=0.8×( )=( )×29=1
11.小明小时走km。照这样计算,他1小时能走( )km,走1km用( )小时。
12.( )千米相当于12千米的,吨是( )吨的。
13.小红骑自行车分钟行千米,她骑自行车每分钟行( )千米,行1千米需要( )分钟。
14.一根彩带长米,用去米,还剩( )米。另一根彩带用去它的,正好是米。这根彩带长( )米。
15.客车和货车同时从A地、B地相对开出,客车每小时行60千米,货车每小时行全程的,当货车行到全程的时,客车已行全程的,则A、B两地间的路程是( )千米。
三、判断题
16.如果A与B的乘积是1,那么A与B互为倒数。( )
17.任何真分数的倒数都是假分数。( )
18.一根木料用去了米,还剩这根木料的,用去的和剩下的同样长。( )
19.男生人数比女生人数多,那么女生人数比男生人数少。( )
20.新光小学四月份用水120吨,比五月份节约了,正好节约了30吨。( )
四、计算题
21.直接写得数。
×= 0÷= ÷3=
÷= ×= 12÷=
22.计算。(能简算的要简算)
×+÷
÷(+) 23-
23.看图列式计算。
五、解答题
24.小明步行千米用小时。照这样计算,他每小时行多少千米,行1千米需要多少小时?
25.习爷爷提出“绿水青山就是金山银山”。科研人员在西北某沙漠的一个区域种植胡杨800棵,种植沙柳的是胡杨棵数的,又是沙枣棵数的,这个区域种植沙枣树多少棵?
26.“迎国庆”书法作品评选活动中,五年级有45件作品获奖,比六年级获奖的作品多,六年级有多少件作品获奖?
27.淘气看一本科普书,第一天看了全书的25%,第二天看了剩下的。
(1)两天正好看了130页,这本书有多少页?
(2)第一天比第二天多看了10页,这本书有多少页?
28.用汽车将一批物资运往灾区,第一次运走总数的,第二次运走余下的,这时还剩下24吨。这批物资一共有多少吨?
29.中国尊是北京一处地标性建筑,它的外形是仿照我国古代用来盛酒的器具“尊”进行设计的,高度为528m,比广州塔矮。广州塔的高度是多少米?
30.一项工程,甲单独做20天完成,乙单独做12天完成,丙单独做15天完成。现在他们合作若干天后,甲中途有事离开,乙丙6天完成了余下的工作。问甲工作了几天?
试卷第11页,共33页
试卷第11页,共33页
参考答案:
题号 1 2 3 4 5
答案 A C A B D
1.A
【分析】求每小时走多少千米,实际上是求小云的速度,根据路程÷时间=速度,代入数据即可得解。
【详解】3÷=3×=4(千米)
即她每小时走4千米。
故答案为:A
【点睛】此题主要根据路程、时间、速度三者之间的关系,利用分数除法的计算,求出结果。
2.C
【分析】根据倒数的意义,乘积是1的两个数互为倒数。因为假分数的分子等于或大于分母,把分子和分母调换位置后,则成了分子小于或等于分母,所以假分数的倒数小于或等于1。据此解答。
【详解】根据分析得,假分数的倒数小于或等于1。
故答案为:C
【点睛】此题考查的目的是理解倒数、假分数的意义,掌握求一个数的倒数的方法。
3.A
【分析】把加工56个零件的工作总量看作单位“1”,根据“工作效率=工作总量÷工作时间”,分别求出甲、乙各自的工作效率,甲、乙的工作效率相加即是合作工效;根据“合作工时=工作总量÷合作工效”,求出甲、乙合作需要的时间。
【详解】甲的工作效率:
乙的工作效率:
(小时)
甲、乙合作需要小时。
正确的算式是。
故答案为:A
4.B
【分析】用榨油总量除以榨油时间,求出平均每小时榨油多少吨,据此列式计算即可。
【详解】根据分析可知,平均每小时榨油:。
故答案为:B
5.D
【分析】一个非零的数如果除以一个大于1的数,商就小于被除数;如果除以一个小于1的数商就大于被除数;如果除以1商就等于被除数;据此解答。
【详解】A.÷1,除数等于1,÷1=;
B.÷6,除数大于1,÷6<;
C.,除数大于1,÷<;
D.,除数小于1,÷>;
故答案为:D
【点睛】本题主要考查了除法算式中,除数的变化,引起商和被除数之间的变化规律。
6.36
【分析】把这根绳子总长看作单位“1”,单位“1”未知,根据分数除法的意义,已知一个数的几分之几是多少,求这个数,用除法,用8除以,即可求出这根绳子的总长。
【详解】8÷=8×=36(m)
即这根绳子总长是36m。
【点睛】此题主要考查分数除法的应用,掌握已知一个数的几分之几是多少,求这个数的计算方法,从而解决问题。
7. 0
【分析】根据倒数的意义,乘积是1的两个数互为倒数,1的倒数是1,0没有倒数,据此解答。
【详解】因为6×=1,所以6和互为倒数;
0没有倒数。
【点睛】此题考查的目的是理解倒数的意义,掌握求倒数的方法及应用,明确:1的倒数是1,0没有倒数。
8. > < >
【分析】一个数(0除外)除以小于1的数,商大于这个数;一个数(0除外)除以大于1的数,商小于这个数;
一个数(0除外)乘小于1的数,积小于这个数;一个数(0除外)乘大于1的数,积大于这个数,据此解答即可。
【详解】>,<,所以>;
<;
>,<,所以>
【点睛】本题属于基础性题目,熟练掌握规律能够提高解答速度,也可以计算出来再比较。
9. 27 15
【分析】一个数的是60,据此可以求出这个数,进而求出这个数的;比的倒数多3的数,我们要先求出的倒数,然后再加上3,即可求出这个数。
【详解】第一空:60÷×
=60××
=27
第二空:的倒数是12
12+3=15
【点睛】本题考查分数乘除法的应用以及倒数的相关知识点。
10. 1.25/
【分析】观察式子,三个算式的乘积都是1,所以本题相当于填、0.8和29的倒数。据此解题。
【详解】×=0.8×1.25=×29=1
或×=0.8×=×29=1。
【点睛】本题考查了倒数的认识,乘积是1的两个数互为倒数,求分数的倒数,将分子分母调换位置即可。
11.
【分析】求平均每小时走多少km,就是求速度,速度=路程÷时间;求平均走1km用多少小时,用时间除以路程。
【详解】÷=(km)
÷=(小时)
【点睛】此题考查了行程问题,掌握分数除法的计算法则是解题关键。除以一个数等于乘这个数的倒数。
12. 9
【分析】把12千米看作单位“1”,求12千米的是多少千米,用乘法计算;把要求的吨数看作单位“1”,已知它的是吨,求这个数,用除法计算。
【详解】12×=9(米)
÷
=×
=(吨)
【点睛】本题考查分数乘、除法的意义及应用,明确求一个数的几分之几是多少,用乘法计算;已知一个数的几分之几是多少,求这个数,用除法计算。
13. 3
【分析】除以一个数等于乘这个数的倒数,第一个空,根据路程÷时间=速度,列式计算;第二个空,根据路程÷速度=时间,列式计算。
【详解】÷=×=(千米)
1÷=1×3=3(分钟)
小红骑自行车分钟行千米,她骑自行车每分钟行千米,行1千米需要3分钟。
14.
【分析】(1)剩下彩带的长度=彩带的总长度-用去部分彩带的长度;
(2)把这根彩带的总长度看作单位“1”,根据“量÷对应的分率”即可求得这根彩带的总长度;据此解答。
【详解】(1)-=(米)
(2)÷=(米)
【点睛】掌握异分母分数加减法的计算方法并找出米对应的分率是解答题目的关键。
15.520
【分析】已知货车每小时行全程的,货车行到全程的时,根据除法的意义,用÷即可求出货车行到全程的需要的时间,也就是小时,客车已行全程的也需要小时;再根据速度×时间=路程,用即可求出全程的是多少千米,也就是325千米,再把全程看作单位“1”,根据分数除法的意义,用即可求出全程。
【详解】
(小时)
(千米)
(千米)
A、B两地间的路程是520千米。
【点睛】本题主要考查了相遇问题,明确客车和货车行驶时间相同是解答本题的关键。
16.√
【分析】乘积是1的两个数互为倒数;据此判断。
【详解】如果A与B的乘积是1,那么A与B互为倒数。
原题说法正确。
故答案为:√
【点睛】本题考查倒数的意义及应用,注意倒数是对两个数而言,是两个数相互依存的一个概念。
17.√
【分析】真分数:分子小于分母的的分数;假分数:分子大于或等于分母的分数;根据求一个倒数的方法,是把一个分数的分子分母互换位置就得到这个分数的倒数,真分数的分子分母互换位置后就变成假分数,可以举例解答。
【详解】如:,的倒数是,是假分数。
任何真分数的倒数都是假分数。
原题干说法正确。
故答案为:√
18.×
【分析】由题意可知,一根木料用去了米,还剩这根木料的,则用去了这根木料的1-=,根据分数除法的意义,可求出这根木料的长度,进而判断即可。
【详解】÷(1-)
=÷
=(米)
-=(米)
则还剩下米,故原题干说法错误。
【点睛】本题考查分数除法,明确分数除法的计算方法是解题的关键。
19.×
【分析】把女生人数看作单位“1”,则男生的人数为1×(1+);然后求出女生人数比男生人数少多少,再除以男生人数即可,据此判断。
【详解】假设女生的人数为1,男生人数为:
1×(1+)
=1×
=
(-1)÷
=÷
=×
=
则女生人数比男生人数少。原题干说法错误。
故答案为:×
【点睛】本题考查求一个数比另一个数少几分之几,明确用除法是解题的关键。
20.×
【分析】将五月份用水量看作单位“1”,未知,则四月份用水量是五月份的(1-),是120吨;用除法求出五月份的用水量,最后求四月份与五月份用水量的差即可。
【详解】120÷(1-)
=120÷
=160(吨)
160-120=40(吨)
所以四月份比五月份节约用水40吨。
故答案为:×
【点睛】本题主要考查“已知一个数的几分之几是多少,求这个数用除法”,找准120吨水对应的分率是解题的关键。
21.;0;
;;16
【解析】略
22.;7;;
;;5
【分析】(1)先把除法转化为乘法,再逆用乘法分配律简算。
(2)先利用乘法分配律去括号,再利用加法结合律简算。
(3)先把除法转化为乘法,再利用乘法交换律、乘法结合律简算。
(4)先算括号里面的,再算括号外面的。
(5)先算小括号里面的,再算中括号里面的,最后算中括号外面的。
(6)先把除法转化为乘法,再算乘法,最后算减法。
【详解】×+÷
=×+×
=(+)×
=1×
=
=
=
=
=6+1
=7
=
=
=
=
=
÷(+)
=÷(+)
=÷
=×
=
=
=
=
=
=
23-
=23-
=23-18
=5
23.192千克
【分析】线段图的意思是,梨有240千克,比苹果多,求苹果有多少千克?
把苹果的质量看作单位“1”,梨的质量比苹果多,则梨的质量是苹果的(1+),单位“1”未知用除法计算,即可求出苹果的质量。
【详解】240÷(1+)
=240÷
=240×
=192(千克)
苹果有192千克。
24.千米;小时
【分析】已知小明步行千米用小时,根据:速度=路程÷时间,用÷,即可求出每小时行驶多少千米;再用1千米除以速度,即可求出需要多少小时。
【详解】(千米)
(小时)
答:小明每小时行千米,行1千米需要小时。
25.600棵
【分析】把胡杨的棵数看作单位“1”,单位“1”已知,根据分数乘法的意义,用800乘求出沙柳的棵数,接着把沙枣的棵数看作单位“1”,单位“1”未知,根据分数除法的意义,用沙柳的棵数除以,即可求出沙枣树的棵数。
【详解】800×÷
=500÷
=600(棵)
答:这个区域种植沙枣树600棵。
【点睛】此题主要考查分数乘除法的意义,注意前后两个单位“1”的不同。
26.36件
【分析】已知五年级有45件作品获奖,比六年级获奖的作品多,可把六年级获奖作品数量看作单位“1”,则五年级获奖作品占六年级的(1+),根据已知一个数的几分之几是多少,求这个数用除法计算,要求得六年级有多少件作品获奖,可列式为:。
【详解】
=45÷
=45×
=36(件)
答:六年级有36件作品获奖。
【点睛】本题考查了分数除法的应用,需要先确定好单位“1”,再结合比较量占单位“1”的具体分率来列式计算。
27.(1)280页
(2)140页
【分析】(1)先把百分数换成分数,25%=,所以剩下了,第二天看了剩下的,即用×,算出第二天看了全书的几分之几,再用130除以第一天和第二天看的占比之和,即可算出书的总页数。
(2)根据题意可知,用13除以第一天和第二天看的占比之差,即可算出答案。
【详解】(1)第一天看的页数占比:25%=
第二天看的页数占比:×
=
=
总页数:
=
=
=
=280(页)
答:这本书一共有280页。
(2)
=
=
=10×14
=140(页)
答:这本书一共有140页。
【点睛】此题考查了学生的理解分析能力以及分数乘除法的运算。
28.48吨
【分析】把这批物资的总数看做单位“1”,第一次运走总数的,剩下总数的(1-);第二次运走余下的,即第二次运走总数的(1-)的,根据求一个数的几分之几是多少,用乘法计算,求出第二次运走总数的几分之几;
先根据减法的意义,用“1”分别减去第一次、第二次运走总数的分率,就是剩下的吨数占总数的几分之几,然后根据已知一个数的几分之几是多少,求这个数,用除法计算,即可求出这批物资的总数。
【详解】第二次运走总数的:
(1-)×
=×
=
总数:
24÷(1--)
=24÷
=24×2
=48(吨)
答:这批物资一共有48吨。
【点睛】本题考查分数乘除法的应用,找出单位“1”,关键是根据分数乘法的意义求出第二次运走总数的几分之几,然后根据分数除法的意义求出总数。
29.600米
【分析】把广州塔的高度看成单位“1”,它的(1-)是528米,根据分数除法的意义,用528除以(1-)即可求出广州塔的高度。
【详解】528÷(1-)
=528÷
=600(米)
答:广州塔的高度是600米。
【点睛】本题的关键是找出单位“1”,并找出数量对应了单位“1”的几分之几,再用除法就可以求出单位“1”的量。
30.天
【分析】把这项工程的量看作单位“1”,先依据工作总量÷工作时间=工作效率,求出甲、乙、丙的工作效率,乙丙6天完成了余下的工作,根据工作总量=工作时间×工作效率,求出乙丙6天完成的工作量,用1减去乙丙6天完成的工作量,求出三人完成的工作量,再根据工作时间=工作量÷三人工作效率和即可求出甲工作了几天。
【详解】1÷20=
1÷12=
1÷15=
1-6×(+)
=1-6×(+)
=1-6×
=1-
=
÷(++)
=÷(++)
=÷
=×
=(天)
答:甲工作了天。
【点睛】本题考查知识点:依据工作时间,工作效率以及工作总量之间数量关系解决问题。
答案第11页,共22页
答案第11页,共22页
