【中考考点基础练】第4章 质量与密度 2025年物理中考总复习(福建)(含答案)
文档属性
| 名称 | 【中考考点基础练】第4章 质量与密度 2025年物理中考总复习(福建)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 210.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-15 09:29:10 | ||
图片预览


文档简介
第4章 质量与密度(2~8分)
【基础作业】
1.(2024·福州模拟)如图所示,学校对初二年级的学生进行了体质健康测试,下面记录了初二学生小东的一组测试数据,你认为测试数据中最不符合小东实际的是 ( )
A.体重500kg B.体温36.8℃
C.身高160cm D.脉搏70次/分钟
2.(2024·莆田一模)如图所示,这是标准大气压下,质量为1g的某液体的体积-温度图像,以下说法正确的是 ( )
A.4℃时,液体密度最小
B.温度升高,液体密度不变
C.1℃时液体的密度比5℃时的大
D.由1℃升高到10℃,液体的密度先变大再变小
3.(2024·泉州二模)甲、乙、丙三种物质的质量与体积的关系如图所示,ρ甲、ρ乙、ρ丙、ρ水分别代表甲、乙、丙三种物质和水的密度,据图可知,下列说法正确的是(ρ水=1.0×103 kg/m3) ( )
A.ρ丙>ρ乙>ρ甲且ρ甲>ρ水
B.ρ甲>ρ乙>ρ丙且ρ丙>ρ水
C.ρ丙<ρ乙<ρ甲且ρ乙=ρ水
D.ρ乙>ρ丙>ρ甲且ρ甲<ρ水
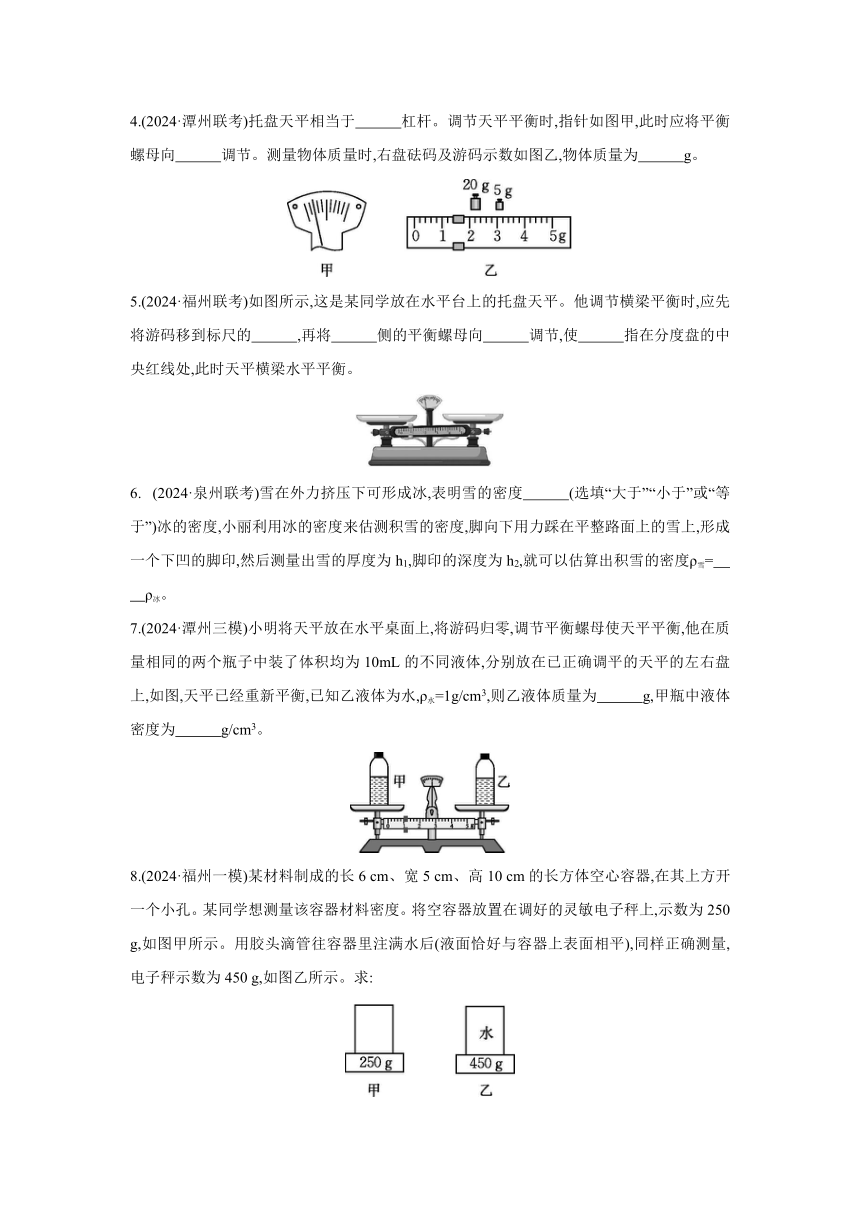
4.(2024·潭州联考)托盘天平相当于 杠杆。调节天平平衡时,指针如图甲,此时应将平衡螺母向 调节。测量物体质量时,右盘砝码及游码示数如图乙,物体质量为 g。
5.(2024·福州联考)如图所示,这是某同学放在水平台上的托盘天平。他调节横梁平衡时,应先将游码移到标尺的 ,再将 侧的平衡螺母向 调节,使 指在分度盘的中央红线处,此时天平横梁水平平衡。
(2024·泉州联考)雪在外力挤压下可形成冰,表明雪的密度 (选填“大于”“小于”或“等于”)冰的密度,小丽利用冰的密度来估测积雪的密度,脚向下用力踩在平整路面上的雪上,形成一个下凹的脚印,然后测量出雪的厚度为h1,脚印的深度为h2,就可以估算出积雪的密度ρ雪=
ρ冰。
7.(2024·潭州三模)小明将天平放在水平桌面上,将游码归零,调节平衡螺母使天平平衡,他在质量相同的两个瓶子中装了体积均为10mL的不同液体,分别放在已正确调平的天平的左右盘上,如图,天平已经重新平衡,已知乙液体为水,ρ水=1g/cm3,则乙液体质量为 g,甲瓶中液体密度为 g/cm3。
8.(2024·福州一模)某材料制成的长6 cm、宽5 cm、高10 cm的长方体空心容器,在其上方开一个小孔。某同学想测量该容器材料密度。将空容器放置在调好的灵敏电子秤上,示数为250 g,如图甲所示。用胶头滴管往容器里注满水后(液面恰好与容器上表面相平),同样正确测量,电子秤示数为450 g,如图乙所示。求:
(1)容器的容积。
(2)容器材料的体积。
(3)容器材料的密度。
【素养作业】
9.(2024·三明一模)(科技时事)我国生产的世界上最薄的不锈钢箔带——手撕钢的厚度只有0.015 mm,则面积为1 m2的手撕钢的质量约为 ( )
A.120 g B.12 g
C.1.2 g D.0.12 g
10.(2024·南平一模)小王买了一种果汁,他想在实验室中测量出这种果汁的密度,主要实验步骤如下:
(1)把天平放在水平台上,将游码移到零刻度线处,指针位置如图甲所示,此时应向 (选填“左”或“右”)调节平衡螺母,直至横梁平衡。
(2)用调节好的天平测量烧杯和果汁的总质量为106 g。
(3)将烧杯中的部分果汁倒入量筒中,如图乙所示,量筒中果汁的体积为 cm3。
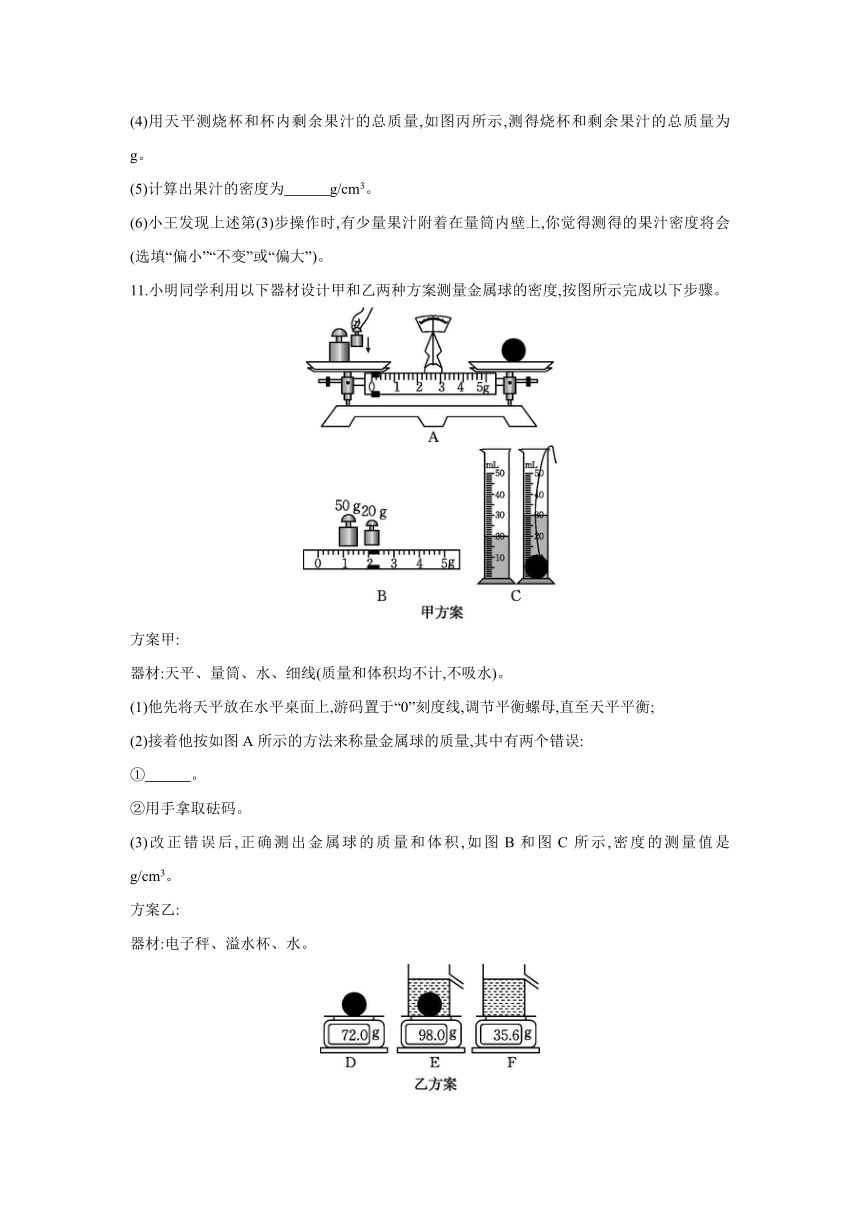
(4)用天平测烧杯和杯内剩余果汁的总质量,如图丙所示,测得烧杯和剩余果汁的总质量为 g。
(5)计算出果汁的密度为 g/cm3。
(6)小王发现上述第(3)步操作时,有少量果汁附着在量筒内壁上,你觉得测得的果汁密度将会 (选填“偏小”“不变”或“偏大”)。
11.小明同学利用以下器材设计甲和乙两种方案测量金属球的密度,按图所示完成以下步骤。
方案甲:
器材:天平、量筒、水、细线(质量和体积均不计,不吸水)。
(1)他先将天平放在水平桌面上,游码置于“0”刻度线,调节平衡螺母,直至天平平衡;
(2)接着他按如图A所示的方法来称量金属球的质量,其中有两个错误:
① 。
②用手拿取砝码。
(3)改正错误后,正确测出金属球的质量和体积,如图B和图C所示,密度的测量值是 g/cm3。
方案乙:
器材:电子秤、溢水杯、水。
①用电子秤测出金属球的质量,如图D所示。
②将金属球放入溢水杯中,然后向溢水杯中注满水,测出总质量,如图E所示。
③缓慢取出金属球,再向溢水杯中补满水,测出此时总质量,如图F所示。
(4)金属球密度的测量值是 g/cm3。实验中取出金属球时会带出一些水,则金属球密度的测量值将 (选填“偏大”“不变”或“偏小”)。
(5)评估:在所有操作均正确的情况下,小明同学发现两种方案测量结果依然有差异,进一步分析发现产生差异的原因是 。
12.暑期,小伟在科技创新大赛中获奖,他想知道所获奖牌的材质,为此,设计了如下实验方案。
(1)把天平放在 上,把游码放到标尺左端的零刻度线处,横梁静止时,指针指在如图甲所示位置,接下来的操作是 ,直至横梁在水平位置平衡。
(2)测量过程中,当天平重新平衡时,右盘中所加砝码和标尺上游码的位置如图乙所示,则奖牌的质量为 g。
(3)在测量奖牌体积时,由于量筒口径较小,奖牌无法放入,经过思考,小伟采取了以下步骤测出了奖牌的密度。
物质 密度/(kg·m-3)
铜 8.9×103
铁 7.9×103
铝 2.7×103
①向烧杯中加入适量的水,用细线系住奖牌使其浸没在水中,并在烧杯壁上水面到达的位置作出标记,如图丙所示。
②把奖牌从水中取出后,将量筒中的水(体积是40 mL)缓慢加入烧杯中至标记处,量筒中剩余水的体积如图丁所示,则奖牌的体积为 cm3。
③算出奖牌的密度是 kg/m3。小伟将测得的密度和表中数据进行对比,推测奖牌可能是由 (答案合理即可)制成的。
13.(2024·厦门期中)一个铝球质量为54g,体积为50cm3,已知ρ铝=2.7×103kg/m3。
(1)试通过计算判断该铝球是空心的还是实心的。
(2)若是空心的,空心部分的体积是多少
(3)若在该球空心部分注满某种液体后,球的总质量为84g,则所注液体的密度是多少
【参考答案】
1.A 2.D 3.C
4.等臂 右 26.4
5.零刻度线处 右 右 指针
6.小于
7.10 1.1
8.解:(1)容器里注满水后,水的质量:
m水=m总-m容器=450 g-250 g=200 g
根据密度公式得,水的体积:
V水===200 cm3
容器的容积V容=V水=200 cm3。
(2)由题知,长方体空心容器总体积:
V总=6 cm×5 cm×10 cm=300 cm3
容器材料的体积:
V材料=V总-V容=300 cm3-200 cm3=100 cm3
(3)容器材料的密度:ρ===2.5 g/cm3。
9.A
10.(1)左 (3)40 (4)62 (5)1.1 (6)偏大
11.(2)砝码放在左边托盘里 (3)7.2 (4)7.5 不变
(5)用电子秤测量体积比量筒更精确
12.(1)水平台 向右调节平衡螺母 (2)70.4 (3)②8 ③8.8×103 铜
13.解:(1)由ρ=可得,铝球的实心体积:
V铝===20cm3
因为V铝(2)空心体积:
V空=V球-V铝=50cm3-20cm3=30cm3
(3)将空心部分注满某种液体后,液体的质量:m'=m总-m球=84g-54g=30g
液体的体积:V'=V空=30cm3
液体的密度:ρ液===1g/cm3。
【基础作业】
1.(2024·福州模拟)如图所示,学校对初二年级的学生进行了体质健康测试,下面记录了初二学生小东的一组测试数据,你认为测试数据中最不符合小东实际的是 ( )
A.体重500kg B.体温36.8℃
C.身高160cm D.脉搏70次/分钟
2.(2024·莆田一模)如图所示,这是标准大气压下,质量为1g的某液体的体积-温度图像,以下说法正确的是 ( )
A.4℃时,液体密度最小
B.温度升高,液体密度不变
C.1℃时液体的密度比5℃时的大
D.由1℃升高到10℃,液体的密度先变大再变小
3.(2024·泉州二模)甲、乙、丙三种物质的质量与体积的关系如图所示,ρ甲、ρ乙、ρ丙、ρ水分别代表甲、乙、丙三种物质和水的密度,据图可知,下列说法正确的是(ρ水=1.0×103 kg/m3) ( )
A.ρ丙>ρ乙>ρ甲且ρ甲>ρ水
B.ρ甲>ρ乙>ρ丙且ρ丙>ρ水
C.ρ丙<ρ乙<ρ甲且ρ乙=ρ水
D.ρ乙>ρ丙>ρ甲且ρ甲<ρ水
4.(2024·潭州联考)托盘天平相当于 杠杆。调节天平平衡时,指针如图甲,此时应将平衡螺母向 调节。测量物体质量时,右盘砝码及游码示数如图乙,物体质量为 g。
5.(2024·福州联考)如图所示,这是某同学放在水平台上的托盘天平。他调节横梁平衡时,应先将游码移到标尺的 ,再将 侧的平衡螺母向 调节,使 指在分度盘的中央红线处,此时天平横梁水平平衡。
(2024·泉州联考)雪在外力挤压下可形成冰,表明雪的密度 (选填“大于”“小于”或“等于”)冰的密度,小丽利用冰的密度来估测积雪的密度,脚向下用力踩在平整路面上的雪上,形成一个下凹的脚印,然后测量出雪的厚度为h1,脚印的深度为h2,就可以估算出积雪的密度ρ雪=
ρ冰。
7.(2024·潭州三模)小明将天平放在水平桌面上,将游码归零,调节平衡螺母使天平平衡,他在质量相同的两个瓶子中装了体积均为10mL的不同液体,分别放在已正确调平的天平的左右盘上,如图,天平已经重新平衡,已知乙液体为水,ρ水=1g/cm3,则乙液体质量为 g,甲瓶中液体密度为 g/cm3。
8.(2024·福州一模)某材料制成的长6 cm、宽5 cm、高10 cm的长方体空心容器,在其上方开一个小孔。某同学想测量该容器材料密度。将空容器放置在调好的灵敏电子秤上,示数为250 g,如图甲所示。用胶头滴管往容器里注满水后(液面恰好与容器上表面相平),同样正确测量,电子秤示数为450 g,如图乙所示。求:
(1)容器的容积。
(2)容器材料的体积。
(3)容器材料的密度。
【素养作业】
9.(2024·三明一模)(科技时事)我国生产的世界上最薄的不锈钢箔带——手撕钢的厚度只有0.015 mm,则面积为1 m2的手撕钢的质量约为 ( )
A.120 g B.12 g
C.1.2 g D.0.12 g
10.(2024·南平一模)小王买了一种果汁,他想在实验室中测量出这种果汁的密度,主要实验步骤如下:
(1)把天平放在水平台上,将游码移到零刻度线处,指针位置如图甲所示,此时应向 (选填“左”或“右”)调节平衡螺母,直至横梁平衡。
(2)用调节好的天平测量烧杯和果汁的总质量为106 g。
(3)将烧杯中的部分果汁倒入量筒中,如图乙所示,量筒中果汁的体积为 cm3。
(4)用天平测烧杯和杯内剩余果汁的总质量,如图丙所示,测得烧杯和剩余果汁的总质量为 g。
(5)计算出果汁的密度为 g/cm3。
(6)小王发现上述第(3)步操作时,有少量果汁附着在量筒内壁上,你觉得测得的果汁密度将会 (选填“偏小”“不变”或“偏大”)。
11.小明同学利用以下器材设计甲和乙两种方案测量金属球的密度,按图所示完成以下步骤。
方案甲:
器材:天平、量筒、水、细线(质量和体积均不计,不吸水)。
(1)他先将天平放在水平桌面上,游码置于“0”刻度线,调节平衡螺母,直至天平平衡;
(2)接着他按如图A所示的方法来称量金属球的质量,其中有两个错误:
① 。
②用手拿取砝码。
(3)改正错误后,正确测出金属球的质量和体积,如图B和图C所示,密度的测量值是 g/cm3。
方案乙:
器材:电子秤、溢水杯、水。
①用电子秤测出金属球的质量,如图D所示。
②将金属球放入溢水杯中,然后向溢水杯中注满水,测出总质量,如图E所示。
③缓慢取出金属球,再向溢水杯中补满水,测出此时总质量,如图F所示。
(4)金属球密度的测量值是 g/cm3。实验中取出金属球时会带出一些水,则金属球密度的测量值将 (选填“偏大”“不变”或“偏小”)。
(5)评估:在所有操作均正确的情况下,小明同学发现两种方案测量结果依然有差异,进一步分析发现产生差异的原因是 。
12.暑期,小伟在科技创新大赛中获奖,他想知道所获奖牌的材质,为此,设计了如下实验方案。
(1)把天平放在 上,把游码放到标尺左端的零刻度线处,横梁静止时,指针指在如图甲所示位置,接下来的操作是 ,直至横梁在水平位置平衡。
(2)测量过程中,当天平重新平衡时,右盘中所加砝码和标尺上游码的位置如图乙所示,则奖牌的质量为 g。
(3)在测量奖牌体积时,由于量筒口径较小,奖牌无法放入,经过思考,小伟采取了以下步骤测出了奖牌的密度。
物质 密度/(kg·m-3)
铜 8.9×103
铁 7.9×103
铝 2.7×103
①向烧杯中加入适量的水,用细线系住奖牌使其浸没在水中,并在烧杯壁上水面到达的位置作出标记,如图丙所示。
②把奖牌从水中取出后,将量筒中的水(体积是40 mL)缓慢加入烧杯中至标记处,量筒中剩余水的体积如图丁所示,则奖牌的体积为 cm3。
③算出奖牌的密度是 kg/m3。小伟将测得的密度和表中数据进行对比,推测奖牌可能是由 (答案合理即可)制成的。
13.(2024·厦门期中)一个铝球质量为54g,体积为50cm3,已知ρ铝=2.7×103kg/m3。
(1)试通过计算判断该铝球是空心的还是实心的。
(2)若是空心的,空心部分的体积是多少
(3)若在该球空心部分注满某种液体后,球的总质量为84g,则所注液体的密度是多少
【参考答案】
1.A 2.D 3.C
4.等臂 右 26.4
5.零刻度线处 右 右 指针
6.小于
7.10 1.1
8.解:(1)容器里注满水后,水的质量:
m水=m总-m容器=450 g-250 g=200 g
根据密度公式得,水的体积:
V水===200 cm3
容器的容积V容=V水=200 cm3。
(2)由题知,长方体空心容器总体积:
V总=6 cm×5 cm×10 cm=300 cm3
容器材料的体积:
V材料=V总-V容=300 cm3-200 cm3=100 cm3
(3)容器材料的密度:ρ===2.5 g/cm3。
9.A
10.(1)左 (3)40 (4)62 (5)1.1 (6)偏大
11.(2)砝码放在左边托盘里 (3)7.2 (4)7.5 不变
(5)用电子秤测量体积比量筒更精确
12.(1)水平台 向右调节平衡螺母 (2)70.4 (3)②8 ③8.8×103 铜
13.解:(1)由ρ=可得,铝球的实心体积:
V铝===20cm3
因为V铝
V空=V球-V铝=50cm3-20cm3=30cm3
(3)将空心部分注满某种液体后,液体的质量:m'=m总-m球=84g-54g=30g
液体的体积:V'=V空=30cm3
液体的密度:ρ液===1g/cm3。
同课章节目录
