17.2.1平面直角坐标系课件
图片预览

文档简介
课件11张PPT。
第3课时 平面直角坐标系1
【教学目标】
1.了解直角坐标系的由来,能够正确画出直角坐标系;
2.通过具体的事例说明在平面上的点用一对有序实数来表示,反过来,每一对有序实数都可以在坐标平面上描出一点;
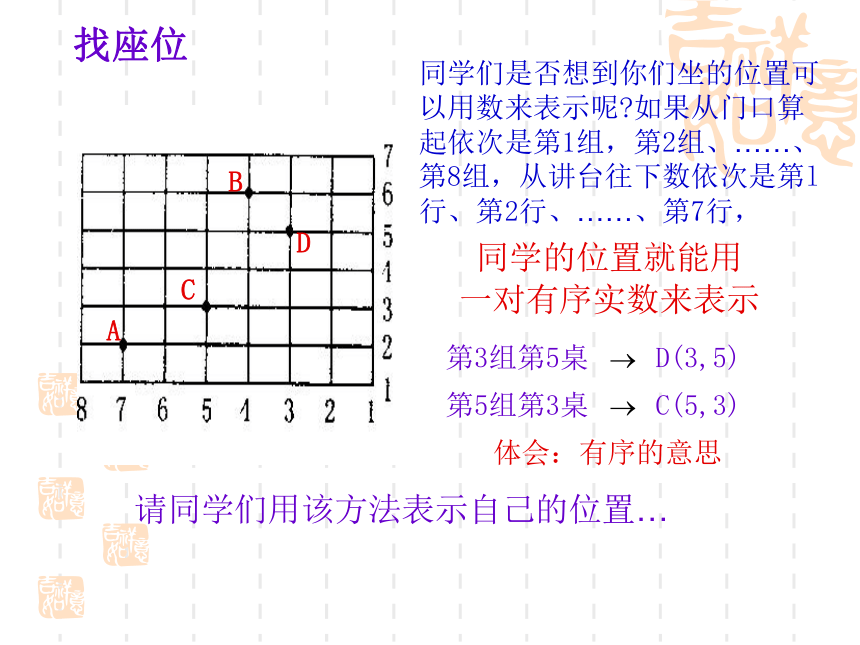
3.掌握象限点、坐标轴上的点的坐标特征.找座位同学们是否想到你们坐的位置可以用数来表示呢?如果从门口算起依次是第1组,第2组、……、第8组,从讲台往下数依次是第l行、第2行、……、第7行, ABCD 同学的位置就能用
一对有序实数来表示 第3组第5桌 D(3,5)第5组第3桌 C(5,3)体会:有序的意思请同学们用该方法表示自己的位置…直角坐标系的建立
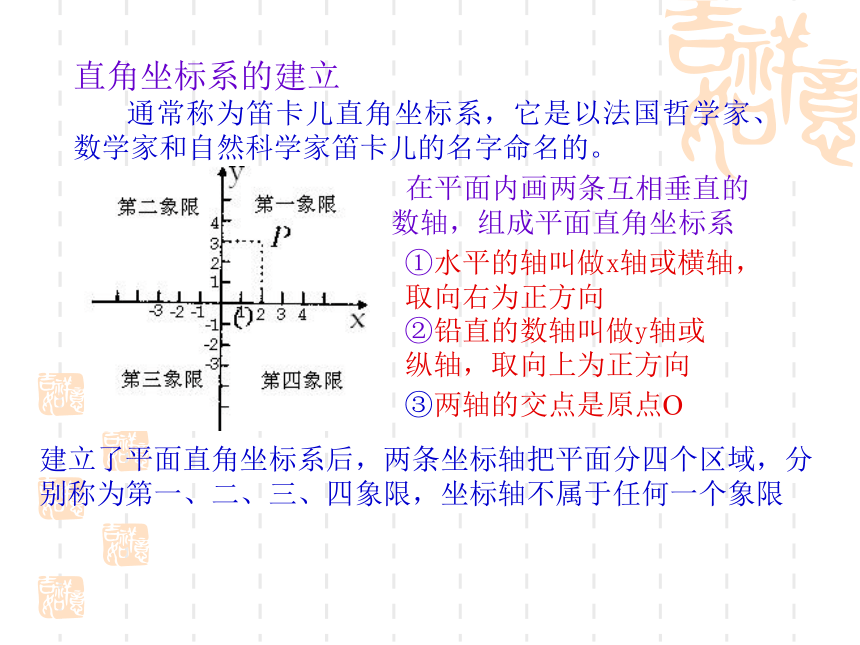
通常称为笛卡儿直角坐标系,它是以法国哲学家、数学家和自然科学家笛卡儿的名字命名的。 在平面内画两条互相垂直的数轴,组成平面直角坐标系①水平的轴叫做x轴或横轴, 取向右为正方向
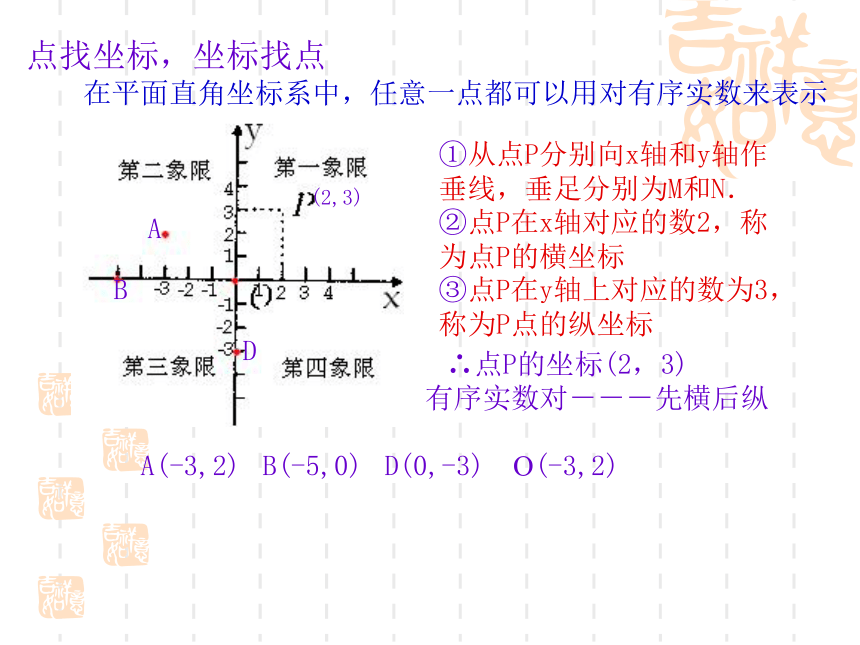
②铅直的数轴叫做y轴或纵轴,取向上为正方向③两轴的交点是原点O建立了平面直角坐标系后,两条坐标轴把平面分四个区域,分别称为第一、二、三、四象限,坐标轴不属于任何一个象限 点找坐标,坐标找点
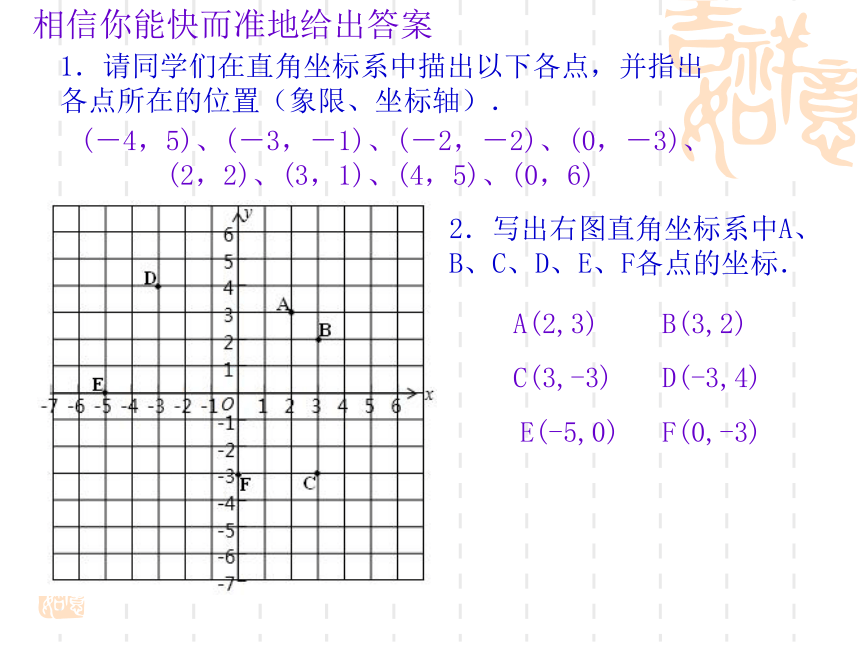
在平面直角坐标系中,任意一点都可以用对有序实数来表示 ①从点P分别向x轴和y轴作垂线,垂足分别为M和N. ②点P在x轴对应的数2,称为点P的横坐标 ③点P在y轴上对应的数为3,称为P点的纵坐标 ∴点P的坐标(2,3) 有序实数对---先横后纵(2,3)BADA(-3,2)B(-5,0)D(0,-3)O(-3,2)相信你能快而准地给出答案 1.请同学们在直角坐标系中描出以下各点,并指出各点所在的位置(象限、坐标轴).(-4,5)、(-3,-1)、(-2,-2)、(0,-3)、
(2,2)、(3,1)、(4,5)、(0,6)2.写出右图直角坐标系中A、B、C、D、E、F各点的坐标.A(2,3)C(3,-3)E(-5,0)B(3,2)D(-3,4)F(0,-3)本节课我们学了哪些新知识点? 1.本节课我们认识了平面直角坐标系,通过上面的讲解和练习可以知道,平面上的点都可以用有序实数来表示,也必须用有序实数表示;反过来,任何一对有序实数都可以在坐标平面上描出一点,所以,在平面直角坐标系中的点和有序实数对是成一一对应的关系。2.象限点坐标的符号特征
第一象限(+,+),第二象限(-,+)
第三象限(-、-),第四象限(+,-)3.坐标轴上的点不属于任何象限
x轴上的点有x的值,其y的值一定为0
y轴上的点有y的值,其x的值一定为0 x轴上的点的纵坐标等于0,反过来,纵坐标等于0的点都在x轴上,y轴上的点的横坐标等于0,反过来,横坐标等于0的点都在y轴上 (+,+)(-,-)(-,+)(+,-)巩固练习,强化概念1 ⑴点P(3,-2)是第 象限内的点;
⑵若点P(3a-6,a)是第二象限内的点,则的取值范围是 ;
⑶如果A(1-a,b+1)在第三象限,那么点B(a,b)在第 象限;
⑷请写出第四象限内的2个点,其横纵坐标和为3,
则为 、 ;
⑸点P(-3,0)是 轴上的点;
⑹如图,长方形ABCO中,AB=3,BC=5,
则A( ),B( ),C( )
⑺变形题:矩形改为等边三角形边长为6三种对称的点坐标的特征MNHK...⑴点B(3,2)与点C(3,-2)关于x轴对称x不变,y变为相反数⑵点D(-3,4)与点F(3,4)关于y轴对称y不变,x变为相反数⑶点K(-3,3)与点H(3,-3)关于原点对称X、y都变为相反数◆若点在第一、三象限角平分线上,它的横坐标等于纵坐标;(同正或同负) 若点在第二、四象限角平分线上,它的横坐标与纵坐标互为相反数巩固练习,强化概念2 ⑴点P(3,-2)关于x轴对称的点的坐标是 ;
点P(3,-2)关于y轴对称的点的坐标是 ;
点P(3,-2)关于原点对称的点的坐标是 ;
⑵若A(a-2,3)和A1(-1,2b+2)关于原点对称,
则a= ,b= ;
⑶已知:点 在y轴上,则点P的坐标是 ; 作业练习册:课本第33页的第1、2、3题.
谢谢大家!
第3课时 平面直角坐标系1
【教学目标】
1.了解直角坐标系的由来,能够正确画出直角坐标系;
2.通过具体的事例说明在平面上的点用一对有序实数来表示,反过来,每一对有序实数都可以在坐标平面上描出一点;
3.掌握象限点、坐标轴上的点的坐标特征.找座位同学们是否想到你们坐的位置可以用数来表示呢?如果从门口算起依次是第1组,第2组、……、第8组,从讲台往下数依次是第l行、第2行、……、第7行, ABCD 同学的位置就能用
一对有序实数来表示 第3组第5桌 D(3,5)第5组第3桌 C(5,3)体会:有序的意思请同学们用该方法表示自己的位置…直角坐标系的建立
通常称为笛卡儿直角坐标系,它是以法国哲学家、数学家和自然科学家笛卡儿的名字命名的。 在平面内画两条互相垂直的数轴,组成平面直角坐标系①水平的轴叫做x轴或横轴, 取向右为正方向
②铅直的数轴叫做y轴或纵轴,取向上为正方向③两轴的交点是原点O建立了平面直角坐标系后,两条坐标轴把平面分四个区域,分别称为第一、二、三、四象限,坐标轴不属于任何一个象限 点找坐标,坐标找点
在平面直角坐标系中,任意一点都可以用对有序实数来表示 ①从点P分别向x轴和y轴作垂线,垂足分别为M和N. ②点P在x轴对应的数2,称为点P的横坐标 ③点P在y轴上对应的数为3,称为P点的纵坐标 ∴点P的坐标(2,3) 有序实数对---先横后纵(2,3)BADA(-3,2)B(-5,0)D(0,-3)O(-3,2)相信你能快而准地给出答案 1.请同学们在直角坐标系中描出以下各点,并指出各点所在的位置(象限、坐标轴).(-4,5)、(-3,-1)、(-2,-2)、(0,-3)、
(2,2)、(3,1)、(4,5)、(0,6)2.写出右图直角坐标系中A、B、C、D、E、F各点的坐标.A(2,3)C(3,-3)E(-5,0)B(3,2)D(-3,4)F(0,-3)本节课我们学了哪些新知识点? 1.本节课我们认识了平面直角坐标系,通过上面的讲解和练习可以知道,平面上的点都可以用有序实数来表示,也必须用有序实数表示;反过来,任何一对有序实数都可以在坐标平面上描出一点,所以,在平面直角坐标系中的点和有序实数对是成一一对应的关系。2.象限点坐标的符号特征
第一象限(+,+),第二象限(-,+)
第三象限(-、-),第四象限(+,-)3.坐标轴上的点不属于任何象限
x轴上的点有x的值,其y的值一定为0
y轴上的点有y的值,其x的值一定为0 x轴上的点的纵坐标等于0,反过来,纵坐标等于0的点都在x轴上,y轴上的点的横坐标等于0,反过来,横坐标等于0的点都在y轴上 (+,+)(-,-)(-,+)(+,-)巩固练习,强化概念1 ⑴点P(3,-2)是第 象限内的点;
⑵若点P(3a-6,a)是第二象限内的点,则的取值范围是 ;
⑶如果A(1-a,b+1)在第三象限,那么点B(a,b)在第 象限;
⑷请写出第四象限内的2个点,其横纵坐标和为3,
则为 、 ;
⑸点P(-3,0)是 轴上的点;
⑹如图,长方形ABCO中,AB=3,BC=5,
则A( ),B( ),C( )
⑺变形题:矩形改为等边三角形边长为6三种对称的点坐标的特征MNHK...⑴点B(3,2)与点C(3,-2)关于x轴对称x不变,y变为相反数⑵点D(-3,4)与点F(3,4)关于y轴对称y不变,x变为相反数⑶点K(-3,3)与点H(3,-3)关于原点对称X、y都变为相反数◆若点在第一、三象限角平分线上,它的横坐标等于纵坐标;(同正或同负) 若点在第二、四象限角平分线上,它的横坐标与纵坐标互为相反数巩固练习,强化概念2 ⑴点P(3,-2)关于x轴对称的点的坐标是 ;
点P(3,-2)关于y轴对称的点的坐标是 ;
点P(3,-2)关于原点对称的点的坐标是 ;
⑵若A(a-2,3)和A1(-1,2b+2)关于原点对称,
则a= ,b= ;
⑶已知:点 在y轴上,则点P的坐标是 ; 作业练习册:课本第33页的第1、2、3题.
谢谢大家!
