7.4二元一次方程与一次函数(25张PPT)
文档属性
| 名称 | 7.4二元一次方程与一次函数(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 753.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-09 00:00:00 | ||
图片预览








文档简介
课件25张PPT。7.4二元一次方程与一次函数第二课时回顾与思考:一:二元一次方程的解与相应的一次函数图象上点对应。以方程 x+y=3 的解为坐标的所有点组成的图形
就是 一次函数 y=3-x 的图象. 二、因为函数和方程有以上关系,所以我们就可以用图象法解决方程问题,也可以用方程的方法解决图象问题。三、用图象法解二元一次方程组的一般步骤:
1.把两个方程都化成函数表达式的形式。
2.画出两个函数的图象。
3.找出交点坐标,交点坐标即为方程组的解。议一议:
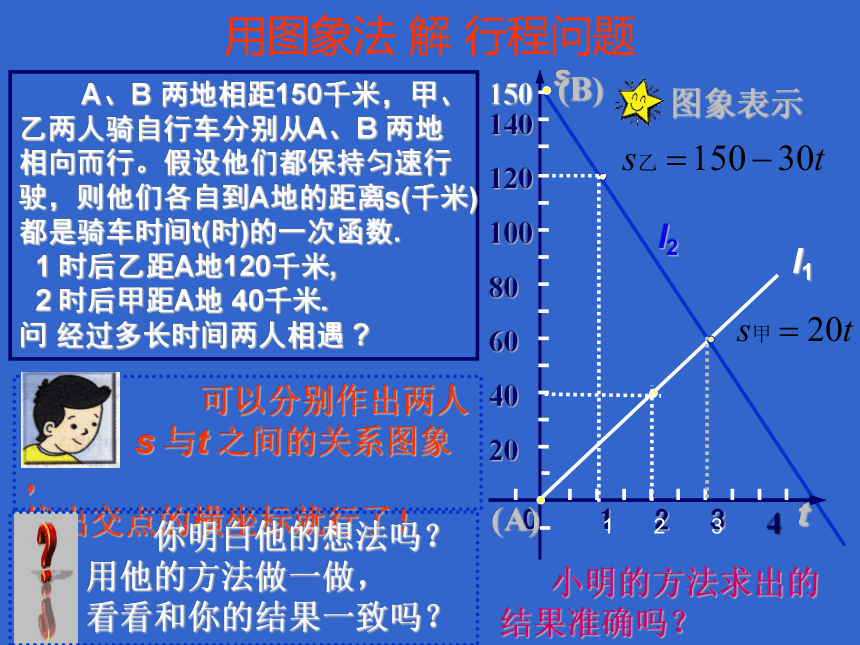
A、B 两地相距150千米,甲、乙两人骑自行车分别从A、B 两地相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离 s(千米)都是骑车时间 t (时)的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问:经过多长时间两人相遇 ? 议一议:
A、B 两地相距150千米,甲、乙两人骑自行车分别从A、B 两地相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离 s(千米)都是骑车时间 t (时)的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问:经过多长时间两人相遇 ? 直线型图表示 A、B 两地相距150千米,甲、乙两人骑自行车分别从A、B 两地相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离s(千米)都是骑车时间t(时)的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问 经过多长时间两人相遇 ? 用图象法 解 行程问题图象表示 可以分别作出两人
s 与t 之间的关系图象,
找出交点的横坐标就行了! 你明白他的想法吗?
用他的方法做一做,
看看和你的结果一致吗? 小明的方法求出的结果准确吗?123 A、B 两地相距150千米,甲、乙两人骑自行车分别从A、B 两地同时相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离s(千米)都是骑车时间t(时)的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问 经过多长时间两人相遇 ? 用方程 解 行程问题小彬 1 时后乙距A地
120千米,即乙的速度是 30千米/时,2 时后甲距A 地 40千米,故甲的速度是 20千米/时, 你明白他的想法吗?用他的方法做一做,看看和你的结果一致吗??t=3 A、B 两地相距150千米,甲、乙两人骑自行车分别从A、B 两地相向而行。假设他们都保持匀速行驶,则他们各自到A 地的距离s (千米) 都是骑车时间 t (时) 的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问 经过多长时间两人相遇 ? 求出s与t之间的关系式,联立解方程组 你明白他的想法吗?
用他的方法做一做,
看看和你的结果一致吗? 对于乙,s 是t
的一次函数,
可设 s=kt+b。
当t=0时,s=150;
当t=1时,s=120。将它们分别代入s=kt+b中,可以求出k、b的值,也即可以求出乙 s 与t 之间的函数表达式。
同样可求出甲s与t之间的函数表达式。
再联立这两个表达式,求解方程组就行了。小颖提示用一元一次方程的方法可以解决问题用图象法可以解决问题用方程组的方法可以解决问题小明小彬小颖 用作图象的方法可以直观地获得问题的结果,但有时却难以准确,为了获得准确的结果,我们一般用代数方法。在以上的解题过程中你受到什么启发?例2、某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(千克)的一次函数。现知李明带了60千克的行李,交了行李费5元;张华带了90千克的行李,交了行李费10元。
(1)写出y与x之间的函数表达式;
(2)旅客最多可免费携带多少千克的行李?解(1)设此一次函数表达式为:y=kx+b(k≠0,k,b为常数)根据题意,可得方程组: 解得:∴y=1/6x—5(2)当x=30时,y=0。
所以旅客最多可免费携带30千克的行李。引例.
如图,l11反映了某公司产品的销售收入与销售量的关系,当销售量为 时,销售收入等于销售成本。
l22反映了该公司产品的销售成本与销售量的关系,根据图意填空:你有什么新的方法解决以前的问题吗?4吨 下图中 l1 ,l2 分别表示 B 离岸起两船相对于海岸的距离s与追赶时间t之间的关系。根据图象回答下列问题:246810O2468t /分s /海里l11l22BA当时间t等于多少分钟时,我边防快艇B能够追赶上A。例2:你有什么新的方法解决以前的问题吗?思考题:
1、某区中学生足球赛共赛8轮(即每队均需参赛8场),胜一场得3分,平一场得1分,负一场得0分。在这次足球联赛中,猛虎队踢平的场数是所负场数的2倍,共得17分,试问该队胜了几场?(要求用图象法求解)
思考题:
1、某区中学生足球赛共赛8轮(即每队均需参赛8场),胜一场得3分,平一场得1分,负一场得0分。在这次足球联赛中,猛虎队踢平的场数是所负场数的2倍,共得17分,试问该队胜了几场?(要求用图象法求解)解:设:胜x场,负y场,则平2y场。
根据题意得:03518/3422xy17/2(2004年湖北中考题)
思考题:
2、已知方程组 ,
所对应的一次函数的图象表示如图,试求出a-b的值。01/2-1XY(贵阳市中考试题)这节课你有什么收获?课外思考题(备用题)1、如图,L1和L2分别表示甲走路和乙骑自行车(在同一条路上)行走的路程s(千米)与时间t(小时)之间的关系,观察图象,回答下列问题:
(1)途中乙发生了什么事,
(2)他们是相遇还是追击;
(3)他们几时相遇。0ts108120.511.2ABDEP0.511.55202510153022.57.522.5如图, 分别表示甲走路与乙骑自行车(在同一条路上)行走的路程s与时间t的关系,观察图象并回答下列问题:补充题0.511.55202510153022.57.522.5(1)乙出发时,与甲相距 ;补充题7.5千米0.511.55202510153022.57.522.5(2)走了一段路程后,乙的自行车发生故障,停下来修理,修车的时间为 小时.补充题10.511.55202510153022.57.522.5(3)乙从出发起,经过 小时与甲相遇;补充题2.50.511.55202510153022.57.522.5(4)甲行走的路程s(km)与时间t(h)之间的函数关系是 .补充题0.511.55202510153022.57.522.5(5)如果乙的自行车不出现故障,那么乙出发后经过 小时与甲相遇,相遇处,离乙的出发点 千米,并在图中标出其相遇点.补充题115课外思考题(备用题)2、用作图象法解方程组7.8——1、2作业:课本P23谢谢成长寄语:
天行健,君子以自强不息。
就是 一次函数 y=3-x 的图象. 二、因为函数和方程有以上关系,所以我们就可以用图象法解决方程问题,也可以用方程的方法解决图象问题。三、用图象法解二元一次方程组的一般步骤:
1.把两个方程都化成函数表达式的形式。
2.画出两个函数的图象。
3.找出交点坐标,交点坐标即为方程组的解。议一议:
A、B 两地相距150千米,甲、乙两人骑自行车分别从A、B 两地相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离 s(千米)都是骑车时间 t (时)的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问:经过多长时间两人相遇 ? 议一议:
A、B 两地相距150千米,甲、乙两人骑自行车分别从A、B 两地相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离 s(千米)都是骑车时间 t (时)的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问:经过多长时间两人相遇 ? 直线型图表示 A、B 两地相距150千米,甲、乙两人骑自行车分别从A、B 两地相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离s(千米)都是骑车时间t(时)的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问 经过多长时间两人相遇 ? 用图象法 解 行程问题图象表示 可以分别作出两人
s 与t 之间的关系图象,
找出交点的横坐标就行了! 你明白他的想法吗?
用他的方法做一做,
看看和你的结果一致吗? 小明的方法求出的结果准确吗?123 A、B 两地相距150千米,甲、乙两人骑自行车分别从A、B 两地同时相向而行。假设他们都保持匀速行驶,则他们各自到A地的距离s(千米)都是骑车时间t(时)的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问 经过多长时间两人相遇 ? 用方程 解 行程问题小彬 1 时后乙距A地
120千米,即乙的速度是 30千米/时,2 时后甲距A 地 40千米,故甲的速度是 20千米/时, 你明白他的想法吗?用他的方法做一做,看看和你的结果一致吗??t=3 A、B 两地相距150千米,甲、乙两人骑自行车分别从A、B 两地相向而行。假设他们都保持匀速行驶,则他们各自到A 地的距离s (千米) 都是骑车时间 t (时) 的一次函数.
1 时后乙距A地120千米,
2 时后甲距A地 40千米.
问 经过多长时间两人相遇 ? 求出s与t之间的关系式,联立解方程组 你明白他的想法吗?
用他的方法做一做,
看看和你的结果一致吗? 对于乙,s 是t
的一次函数,
可设 s=kt+b。
当t=0时,s=150;
当t=1时,s=120。将它们分别代入s=kt+b中,可以求出k、b的值,也即可以求出乙 s 与t 之间的函数表达式。
同样可求出甲s与t之间的函数表达式。
再联立这两个表达式,求解方程组就行了。小颖提示用一元一次方程的方法可以解决问题用图象法可以解决问题用方程组的方法可以解决问题小明小彬小颖 用作图象的方法可以直观地获得问题的结果,但有时却难以准确,为了获得准确的结果,我们一般用代数方法。在以上的解题过程中你受到什么启发?例2、某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需购买行李票,且行李费y(元)是行李质量x(千克)的一次函数。现知李明带了60千克的行李,交了行李费5元;张华带了90千克的行李,交了行李费10元。
(1)写出y与x之间的函数表达式;
(2)旅客最多可免费携带多少千克的行李?解(1)设此一次函数表达式为:y=kx+b(k≠0,k,b为常数)根据题意,可得方程组: 解得:∴y=1/6x—5(2)当x=30时,y=0。
所以旅客最多可免费携带30千克的行李。引例.
如图,l11反映了某公司产品的销售收入与销售量的关系,当销售量为 时,销售收入等于销售成本。
l22反映了该公司产品的销售成本与销售量的关系,根据图意填空:你有什么新的方法解决以前的问题吗?4吨 下图中 l1 ,l2 分别表示 B 离岸起两船相对于海岸的距离s与追赶时间t之间的关系。根据图象回答下列问题:246810O2468t /分s /海里l11l22BA当时间t等于多少分钟时,我边防快艇B能够追赶上A。例2:你有什么新的方法解决以前的问题吗?思考题:
1、某区中学生足球赛共赛8轮(即每队均需参赛8场),胜一场得3分,平一场得1分,负一场得0分。在这次足球联赛中,猛虎队踢平的场数是所负场数的2倍,共得17分,试问该队胜了几场?(要求用图象法求解)
思考题:
1、某区中学生足球赛共赛8轮(即每队均需参赛8场),胜一场得3分,平一场得1分,负一场得0分。在这次足球联赛中,猛虎队踢平的场数是所负场数的2倍,共得17分,试问该队胜了几场?(要求用图象法求解)解:设:胜x场,负y场,则平2y场。
根据题意得:03518/3422xy17/2(2004年湖北中考题)
思考题:
2、已知方程组 ,
所对应的一次函数的图象表示如图,试求出a-b的值。01/2-1XY(贵阳市中考试题)这节课你有什么收获?课外思考题(备用题)1、如图,L1和L2分别表示甲走路和乙骑自行车(在同一条路上)行走的路程s(千米)与时间t(小时)之间的关系,观察图象,回答下列问题:
(1)途中乙发生了什么事,
(2)他们是相遇还是追击;
(3)他们几时相遇。0ts108120.511.2ABDEP0.511.55202510153022.57.522.5如图, 分别表示甲走路与乙骑自行车(在同一条路上)行走的路程s与时间t的关系,观察图象并回答下列问题:补充题0.511.55202510153022.57.522.5(1)乙出发时,与甲相距 ;补充题7.5千米0.511.55202510153022.57.522.5(2)走了一段路程后,乙的自行车发生故障,停下来修理,修车的时间为 小时.补充题10.511.55202510153022.57.522.5(3)乙从出发起,经过 小时与甲相遇;补充题2.50.511.55202510153022.57.522.5(4)甲行走的路程s(km)与时间t(h)之间的函数关系是 .补充题0.511.55202510153022.57.522.5(5)如果乙的自行车不出现故障,那么乙出发后经过 小时与甲相遇,相遇处,离乙的出发点 千米,并在图中标出其相遇点.补充题115课外思考题(备用题)2、用作图象法解方程组7.8——1、2作业:课本P23谢谢成长寄语:
天行健,君子以自强不息。
同课章节目录
- 第七章 二元一次方程组
- 1 二元一次方程组
- 2 解二元一次方程组
- 3 二元一次方程组的应用
- 4 二元一次方程与一次函数
- *5 三元一次方程组
- 第八章 平行线的有关证明
- 1 定义与命题
- 2 证明的必要性
- 3 基本事实与定理
- 4 平行线的判定定理
- 5 平行线的性质定理
- 6 三角形内角和定理
- 第九章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
- 第十章 三角形的有关证明
- 1 全等三角形
- 2 等腰三角形
- 3 直角三角形
- 4 线段的垂直平分线
- 5 角平分线
- 第十一章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
