前三章练习卷(含解析)2024-2025学年苏科版九年级数学上学期期中复习(南京专用)
文档属性
| 名称 | 前三章练习卷(含解析)2024-2025学年苏科版九年级数学上学期期中复习(南京专用) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 15:56:03 | ||
图片预览

文档简介
前三章练习卷-----2024-2025学年苏科版九年级数学上学期期中复习(南京专用)
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.解一元二次方程,配方后正确的是( )
A. B. C. D.
2.若九年级五名男生的体重(单位:kg)分别为50,53,51,55,55,则这五位男生体重的中位数、众数分别是( )
A.53和52 B.53和55 C.55和53 D.51和55
3.已知是关于x的一元二次方程的一个根,则m的值是( )
A. B. C.1 D.2
4.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.8
5.二次三项式-4x+7配方的结果是( )
A.+7 B.+3 C.+3 D.-1
6.如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为( )
A.5﹣4 B.﹣1 C.6﹣2 D.
7.某班45名同学某天每人的生活费用统计如表:
生活费(元) 10 15 20 25 30
学生人数(人) 4 10 15 10 6
对于这45名同学这天每人的生活费用,下列说法错误的是( )
A.平均数是20 B.众数是20 C.中位数是20 D.极差是20
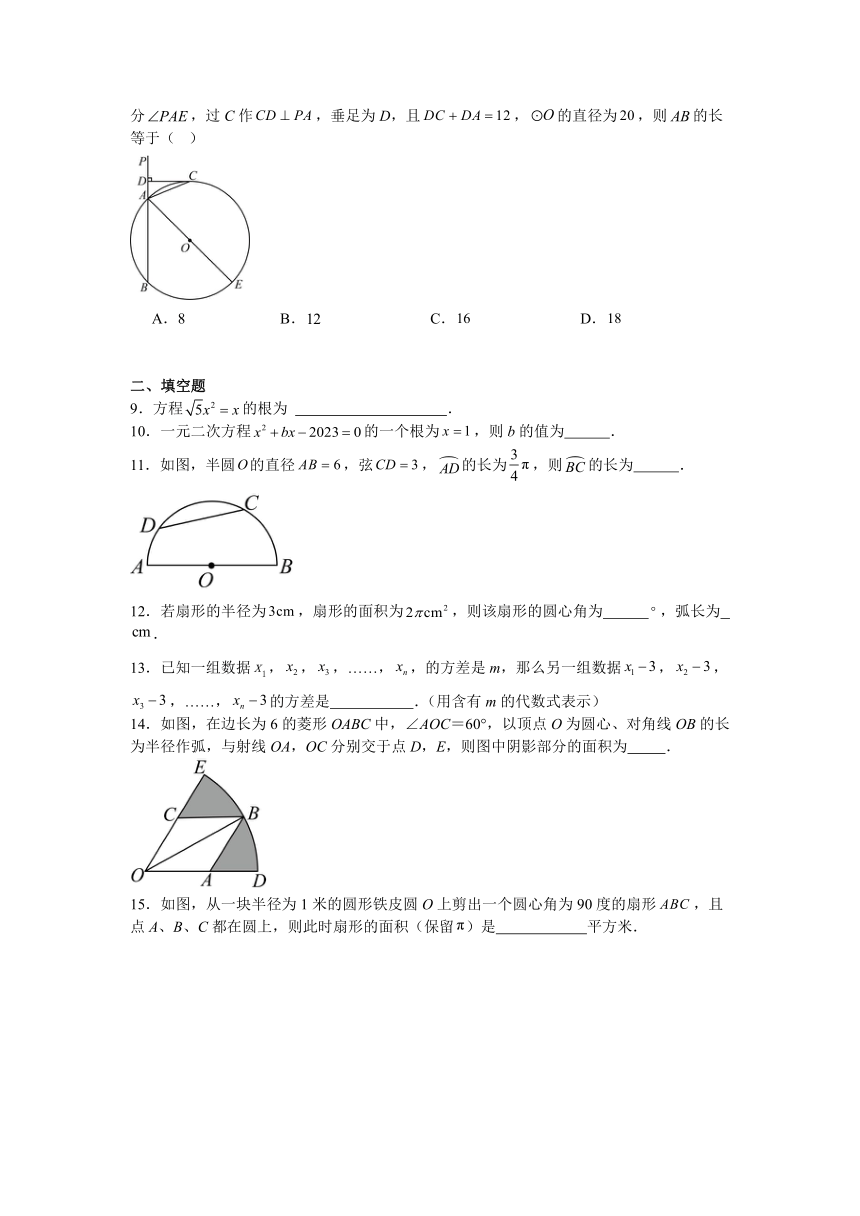
8.如图,已知直线交于两点,是的直径,点C为上一点,且平分,过C作,垂足为D,且,的直径为,则的长等于( )
A.8 B. C. D.
二、填空题
9.方程的根为 .
10.一元二次方程的一个根为,则b的值为 .
11.如图,半圆的直径,弦,的长为,则的长为 .
12.若扇形的半径为,扇形的面积为,则该扇形的圆心角为 ,弧长为 .
13.已知一组数据,,,……,,的方差是m,那么另一组数据,,,……,的方差是 .(用含有m的代数式表示)
14.如图,在边长为6的菱形OABC中,∠AOC=60°,以顶点O为圆心、对角线OB的长为半径作弧,与射线OA,OC分别交于点D,E,则图中阴影部分的面积为 .
15.如图,从一块半径为1米的圆形铁皮圆O上剪出一个圆心角为90度的扇形,且点A、B、C都在圆上,则此时扇形的面积(保留)是 平方米.
16.AC是⊙O的直径,弦BD⊥AC于点E,连接BC,过点O作OF⊥BC于点F,若BD=12cm,OE=cm,则OF= cm.
17.如图,△ABC中,若AC=4,BC=3,AB=5,则△ABC的内切圆半径是 .
18.已知:如图,在中,弦、相交于点,,,,则 .
三、解答题
19.解方程:
(1)
(2);
20.如今网上购物已经成为一种时尚,某网店“双十一”全天交易额逐年增长,2015年交易额为40万元,2017年交易额为48.4万元,求2015年至2017年“双十一”交易额的年平均增长率?
21.某新能源汽车区域销售部希望确定一个适当的季度目标,对完成目标的员工进行奖励,以调动员工的积极性.现对名员工某季度的销售额进行统计和分析.
数据收集(单位:万元):.
数据整理:
销售额/万元
频数
数据分析:
平均数 众数 中位数
问题解决:
(1)填空:______,______.
(2)若将万元作为销售目标,则有______名员工获得奖励.
(3)销售部对数据分析后,最终对一半的员工进行了奖励.员工甲反应:“我这个季度的销售额是万元,比平均数万元高,所以我的销售额超过了一半的员工,为什么我没有拿到奖励?”请你从数学的角度给出合理的回复.
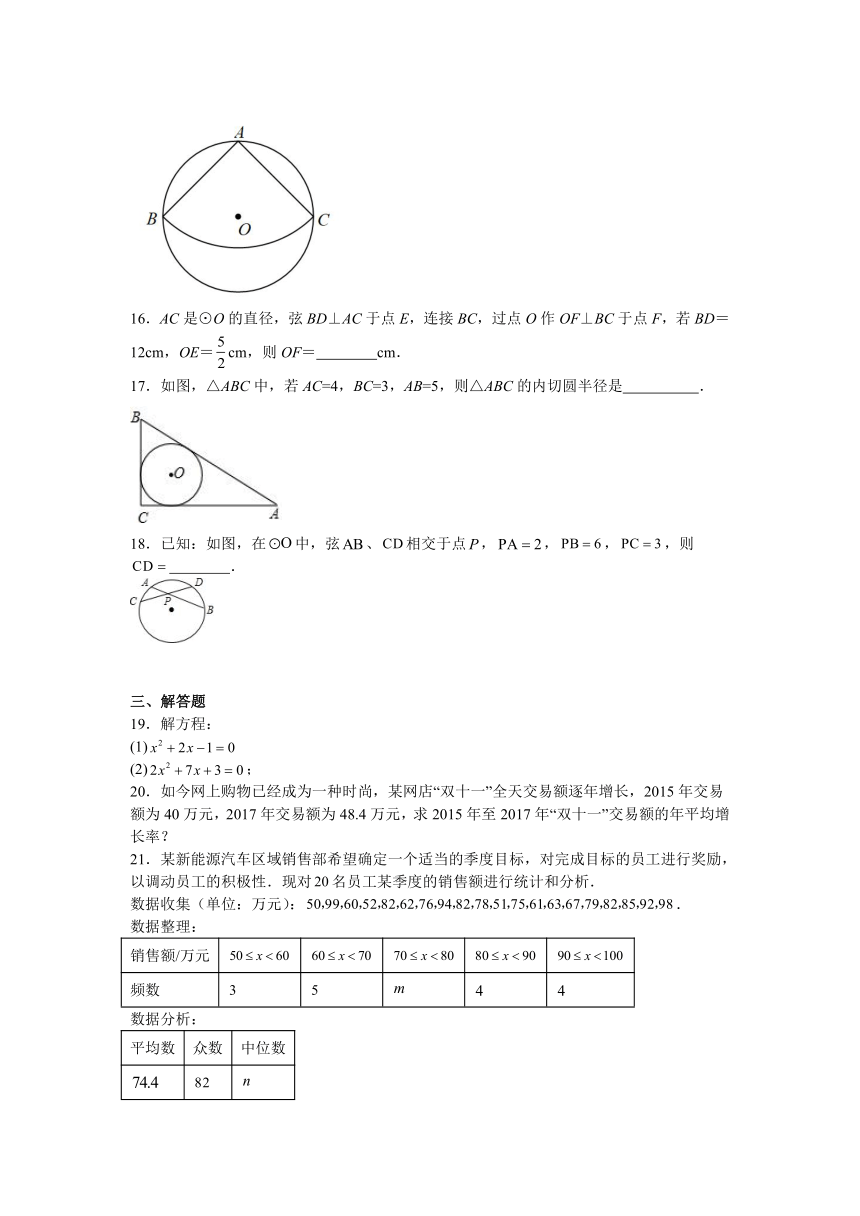
22.如图,的内接四边形中两组对边的延长线分别相交于点,且,求的度数.
23.如图,为的直径,点C,D为圆上两点,,且有平分,过C作于E.
(1)求证:为的切线
(2)若,求半径.
24.某商场统计了某品牌商品2月份到4月份的销量,该品牌商品2月份销售100件,4月份销售144件,且从2月份到4月份销售量的月增长率相同.
(1)求该品牌商品销售量的月增长率;
(2)若此种商品的进价为每件30元,销售过程中发现,当售价为每件40元时,月销售量为200件,若在此基础上每件售价上涨1元,则月销售量将减少5件,为使月销售利润达到2625元,而且尽可能让顾客得到实惠,则该品牌商品的实际售价应定为每件多少元?
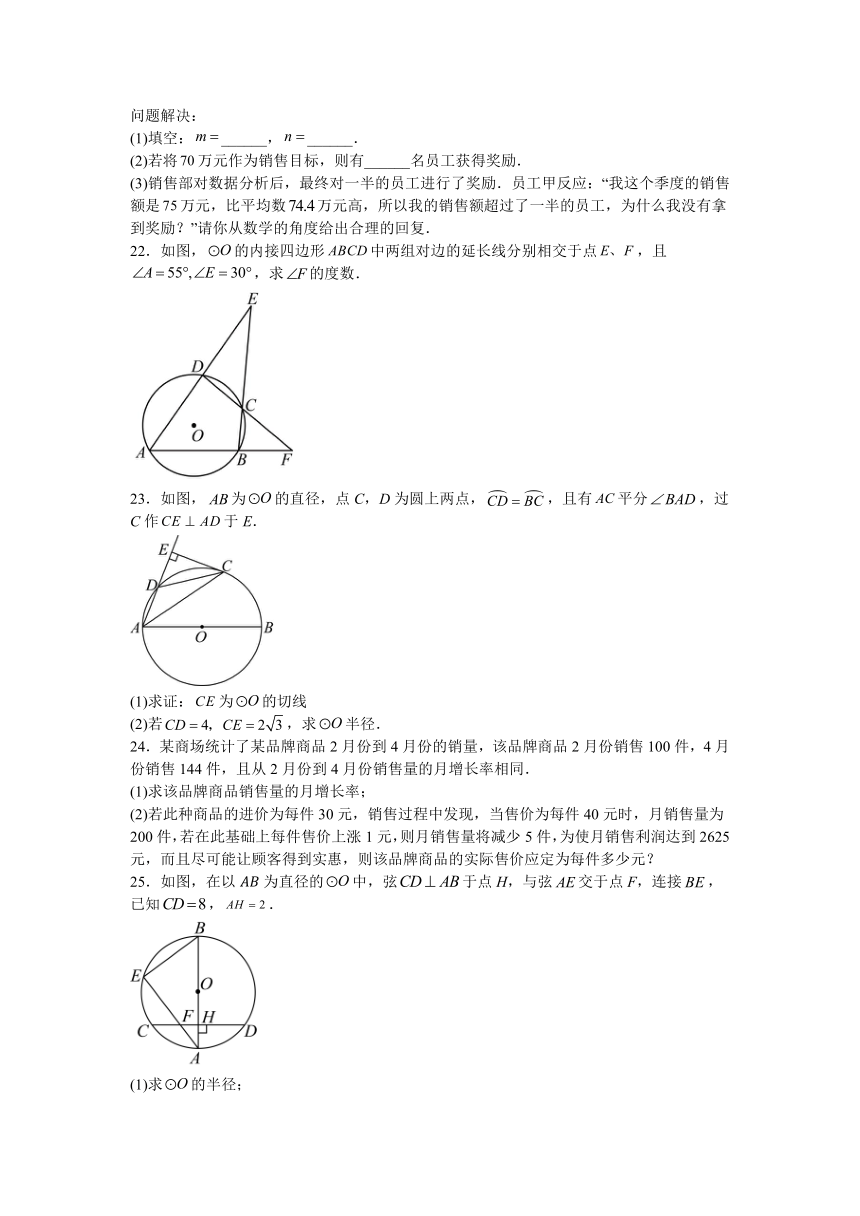
25.如图,在以为直径的中,弦于点H,与弦交于点F,连接,已知,.
(1)求的半径;
(2)若,求的长.
26.如图,已知,交于点B,.
(1)求的度数;
(2)求弧的度数.
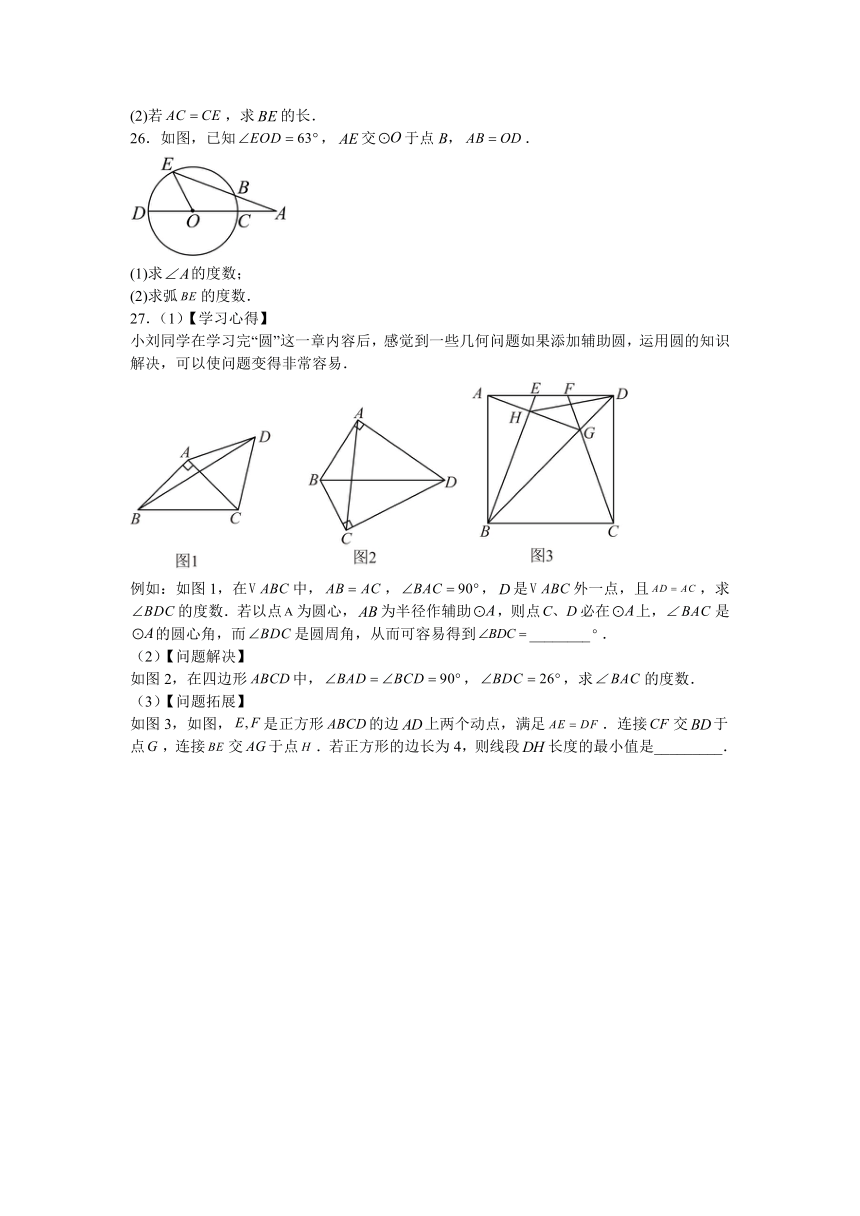
27.(1)【学习心得】
小刘同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.
例如:如图1,在中,,,是外一点,且,求的度数.若以点为圆心,为半径作辅助,则点必在上,是的圆心角,而是圆周角,从而可容易得到________.
(2)【问题解决】
如图2,在四边形中,,,求的度数.
(3)【问题拓展】
如图3,如图,是正方形的边上两个动点,满足.连接交于点,连接交于点.若正方形的边长为4,则线段长度的最小值是_________.
参考答案:
题号 1 2 3 4 5 6 7 8
答案 C B D C B A A B
1.C
【分析】题考查了用配方法解一元二次方程,解本题的关键在熟练掌握用配方法解一元二次方程的方法.配方法解一元二次方程的方法:将常数项移至方程的右边,然后两边都加上一次项系数的一半的平方配方成完全平方后,再开方.
【详解】解:
,
故选C.
2.B
【分析】中位数是按顺序排列的一组数据中居于中间位置的数,众数是一组数据中出现次数最多的数值.
【详解】解:将这组数据重新排列为50、51、53、55、55,
所以这组数据的中位数为53,众数为55,
故选:B.
【点睛】本题考查中位数、众数的求解.掌握各自定义是解题关键.
3.D
【分析】将代入求解即可.
【详解】解:∵是关于x的一元二次方程的一个根,
∴,
∴,
故选:D.
【点睛】此题考查了一元二次方程的根的定义,熟记定义是解题的关键.
4.C
【分析】根据垂径定理得出BC=AB,再根据勾股定理求出OC的长.
【详解】∵OC⊥AB,AB=16,
∴BC=AB=8.
在Rt△BOC中,OB=10,BC=8,
∴.
故选C.
5.B
【详解】把二次三项式-4x+7配方为:
.
故选B.
6.A
【分析】作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,根据两点之间线段最短得到此时PM+PN最小,再利用对称确定A′的坐标,接着利用两点间的距离公式计算出A′B的长,然后用A′B的长减去两个圆的半径即可得到MN的长,即得到+PN的最小值.
【详解】作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,
则此时PM+PN最小,
∵点A坐标(2,3),
∴点A′坐标(2,﹣3),
∵点B(3,4),
∴A′B==5,
∴MN=A′B﹣BN﹣A′M=5﹣3﹣1=5﹣4,
∴PM+PN的最小值为5﹣4.
故选A.
【点睛】本题考查了圆的综合题:掌握与圆有关的性质和关于x轴对称的点的坐标特征;会利用两点之间线段最短解决线段和的最小值问题;会运用两点间的距离公式计算线段的长;理解坐标与图形性质.
7.A
【详解】试题分析:根据众数、中位数、极差、平均数的概念求解.
解:这组数据中位数是20,
则众数为:20,
平均数为:20.4,
极差为:30﹣10=20.
故选A.
考点:众数;加权平均数;中位数;极差.
8.B
【分析】连接,根据题意可证得,再根据角平分线的性质,得,过O作,则,得四边形为矩形,设,在中,由勾股定理得,从而求得x的值,由勾股定理得出的长.
【详解】连接,过O作,垂足为F,
,
,
平分,
,
,
,
,
,
四边形为矩形,
.
,
设,则,
的直径为,
,
,
在中,由勾股定理得.
即,
解得.
,故舍去,
,
,
,由垂径定理知,F为的中点,
.
故选:B.
【点睛】本题主要考查角平分线的性质,勾股定理、矩形的判定和性质以及垂径定理,做辅助线构建矩形是解题的关键.
9.,
【分析】本题考查了因式分解法解一元二次方程.熟练掌握因式分解法解一元二次方程是解题的关键.
利用因式分解法解一元二次方程即可.
【详解】解:,
,
,
∴,,
解得,,,
故答案为:,.
10.2022
【分析】将x=1代入原方程即可求解.
【详解】将x=1代入原方程得:1+b-2023=0,解得:b=2022;
故答案为:2022.
【点睛】本题主要考查了一元二次方程的根,掌握一元二次方程的根的定义是解题的关键.
11.
【分析】由题意可知:是等边三角形,从而可求出弧的长度,再求出半圆弧的长度后,即可求出弧的长度.
【详解】解:连接、,
,
是等边三角形,
,
的长,
又半圆弧的长度为:,
.
故答案为:
【点睛】本题考查圆了弧长的计算,等边三角形的性质等知识,属于中等题型.
12. /
【分析】本题主要考查了求扇形圆心角度数,求扇形弧长,设该扇形圆心角为,根据扇形面积公式得到,解得,再由弧长计算公式进行求解即可.
【详解】解:设该扇形圆心角为,
由题意得,,
解得,
∴该扇形圆心角为,
∴该扇形的弧长为,
故答案为:;.
13.m
【分析】根据方差的性质,直接求解即可.
【详解】解:∵数据,,,……,的方差是m,
∴由于另一组数据,,,……,是在原数据基础上每个数据都减去3,
∴新数据的波动幅度没有发生改变,
∴另一组数据,,,……,的方差是m,
故答案是:m.
【点睛】本题主要考查方差,解题的关键是掌握方差的性质:在原来每个数据都加上或减去同一个数,数据的方差不变.
14.18π﹣18
【分析】连接AC,交OB于H,根据菱形的性质可得∠COH∠AOC=30°,AC=2CH,OB=2OH,利用含30°角的直角三角形的性质及勾股定理可求出CH、OH的长,即可求出AC和OB的长,利用阴影部分的面积=S扇形OED-S菱形OABC即可得答案.
【详解】连接AC,交OB于H,
∵四边形OABC为菱形,∠AOC=60°,
∴∠COH∠AOC=30°,AC=2CH,OB=2OH,
∴CH=3,OH3,
∴AC=6,OB=6,
∴阴影部分的面积66=18π﹣18,
故答案为18π﹣18.
【点睛】本题考查了菱形的性质及扇形面积,菱形的四条边相等,对角线互相垂直且平分对角;熟练掌握菱形的性质及扇形的面积公式是解题关键.
15.
【分析】连接,先根据圆周角定理可得是的直径,再利用勾股定理可得,然后利用扇形的面积公式求解即可得.
【详解】解:如图,连接,
由题意得:,,
是的直径,
米,
,
,
则此时扇形的面积是(平方米),
故答案为:.
【点睛】本题考查了圆周角定理、扇形的面积、勾股定理,熟练掌握扇形的面积公式是解题关键.
16.或
【分析】根据题意分两种情况并综合利用垂径定理和勾股定理以及圆的基本性质进行分析即可求解.
【详解】解:如图,连接BO
∵AC是⊙O的直径,弦BD⊥AC于点E,BD=12cm,
∴,
∵OE=cm,BD⊥AC,
∴cm,
∴,,
∵OF⊥BC,
∴,
∴,
如图,
∵OE=cm,BD⊥AC, ,
∴,
∵OF⊥BC,
∴,
∴.
故答案为:或.
【点睛】本题考查圆的综合问题,熟练掌握并利用垂径定理和勾股定理以及圆的基本性质进行分析是解题的关键.注意未作图题一般情况下要进行分类作图讨论.
17.1
【分析】先利用勾股定理的逆定理得到△ABC为直角三角形,∠ACB=90°,然后利用△ABC的内切圆半径R=进行计算.
【详解】∵AC=4,BC=3,AB=5,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,∠ACB=90°,
∴△ABC的内切圆半径R==1.
故答案为:1.
【点睛】本题考查了三角形内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心.也考查了勾股定理的逆定理.
18.7
【分析】连结AC、DB,证△ACP∽△DBP,根据相似三角形对应成比例得到PD的长,进而得到CD的长.
【详解】如图,连结AC、DB,
根据同弧所对的圆周角相等,得到∠ACP=∠DBP,
又因为∠APC=∠DPB,
因此△ACP∽△DBP,
故PA:PC=PD:PB,
因此PD=4,
故CD=PC+PD =7.
【点睛】本题主要考查同弧所对的圆周角相等以及相似三角形的判定和性质,熟练掌握并活用这些知识点是解答此题的关键.
19.(1)
(2),;
【分析】(1)根据配方法解一元二次方程,即可求解;
(2)先化为整式方程,解方程即可求解,最后要检验.
【详解】(1)解:,
∴,
∴,
∴,
解得:;
(2)解:,
∴,,,
∴,
∴,
∴,;
【点睛】本题考查了解一元二次方程,解分式方程,正确的计算是解题的关键.
20.2015年至2017年“双十一”交易额的年平均增长率为10%.
【分析】设2015年至2017年“双十一”交易额的年平均增长率为x,根据2015年及2017年该网店“双十一”全天交易额,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
【详解】解:设2015年至2017年“双十一”交易额的年平均增长率为x,
根据题意得:40(1+x)2=48.4,
解得:x1=0.1=10%,x2=﹣2.1.
答:2015年至2017年“双十一”交易额的年平均增长率为10%.
【点睛】考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
21.(1),;
(2);
(3)见解析.
【分析】()利用频数和中位数的定义解答即可;
()利用表格一的信息解答即可;
()利用中位数的定义解答即可;
本题考查了数据与统计,数据的分析与整理,平均数,众数,中位数与频数,熟练掌握上述数据的特征是解题的关键.
【详解】(1)解:,
将个数据按由大到小的顺序排列如下: , 位置在中间的两个数为,它们的平均数为,
∴这组数据的中位数为,
∴,
故答案为:,;
(2)解:由个数据可知,不低于万元的个数为,
∴若将月销售额不低于万元确定为销售目标,则有名员工获得奖励,
故答案为:;
(3)解:由()可知,名员工的销售额的中位数为万元,
∴名员工的销售额有一半的人,即人超过万元,
公司对一半的员工进行了奖励,说明销售额在万元及以上的人才能获得,
而员工甲的销售额是万元,低于万元,
∴员工甲不能拿到奖励.
22..
【分析】本题考查了圆内接四边形的性质,三角形的外角性质,三角形内角和定理,熟练掌握其性质是解题的关键.先根据三角形外角性质计算出,再根据圆内接四边形的性质计算出,然后再根据三角形外角性质求.
【详解】,
,
为圆内接四边形
,
,
,
.
23.(1)见解析
(2)
【分析】(1)如图:连接,由角平分线的定义及等腰三角形的性质可得,即可得,进而得到即可证明结论;
(2)如图∶连接,过C作于F.根据角平分线的性质定理可得,由圆周角定理可得,再由勾股定理可得;设半径为R,则在中运用勾股定理列关于R的方程求解即可.
【详解】(1)证明:如图:连接,
∵平分,
∴,
∵,
∴,
∴,
∴,
∴,
∵,即,
∴,即,
∵是半径,
∴为的切线.
(2)解:如图∶连接,过C作于F.
∵平分,,
∴,
∵,
∴,
∴
设半径为R,则在中,,
∴,解得:.
【点睛】本题主要考查了切线的判定、圆周角定理、等腰三角形的性质、角平分线的性质定理、勾股定理等知识点,灵活运用相关性质定理成为解题的关键.
24.(1)该品牌商品销售量的月增长率是;
(2)该品牌商品的实际售价应定为每件元.
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)设该品牌商品销售量的月增长率为,根据该品牌商品2月份及4月份的销售量,即可得出关于的一元二次方程,解之取其正值即可得出结论;
(2)设该品牌商品的实际售价应定为每件元,则每件的销售利润为元,月销售量为件,根据月销售利润每件的销售利润月销售量,即可得出关于的一元二次方程,解之取其较小值即可得出结论.
【详解】(1)解:设该品牌商品销售量的月增长率为,依题意,得:
,
解得:,(不合题意,舍去),
答:该品牌商品销售量的月增长率为;
(2)解:设该品牌商品的实际售价应定为每件元,则每件的销售利润为元,月销售量为件,依题意,得:
,
整理得:,
解得:,,
∵尽可能让顾客得到实惠,
,
答:该品牌商品的实际售价应定为每件元.
25.(1)5
(2)6
【分析】本题考查了垂径定理、勾股定理,熟练掌握以上知识点,添加适当的辅助线是解此题的关键.
(1)连接,设半径,由垂径定理可得,从而得到,由勾股定理进行计算即可得出答案;
(2)由(1)得:直径,,,证明出,从而得到,最后由勾股定理计算即可.
【详解】(1)解:如图,连接,
设半径,
,,,是的直径,
,,
,
解得,
的半径为;
(2)解:由(1)得:直径,,,
∵
∴,
,
,
.
26.(1)
(2)
【分析】本题考查了圆心角、弧、弦的关系,等腰三角形的性质,三角形外角的性质,关键是根据三角形内角和定理和三角形外角的性质解答.
(1)连接,由,则,于是,而,得,由,根据,即可得到的度数.
(2)由(1)得,由平角的定义得的度数,从而可求出弧的度数.
【详解】(1)解:连接,如图,
∵,,
∴,
∴,
∴,
而,得,
∴,
而,
∴,
∴.
(2)解:由(1)得,,
又,
∴
∴弧的度数为.
27.(1);(2);(3)
【分析】(1)利用同弧所对的圆周角是所对圆心角的一半求解.
(2)由、、、共圆,得出,
(3)根据正方形的性质可得,,,然后利用“边角边”证明和全等,根据全等三角形对应角相等可得,利用“”证明和全等,根据全等三角形对应角相等可得,从而得到,然后求出,取的中点,连接、,根据直角三角形斜边上的中线等于斜边的一半可得,利用勾股定理列式求出,然后根据三角形的三边关系可知当、、三点共线时,的长度最小.
【详解】解:(1)如图1,
,,
以点为圆心,点、、必在上,
是的圆心角,而是圆周角,
,
故答案是:;
(2)如图2,取的中点,连接、.
,
点、、、共圆,
,
,
,
(3)如图3,在正方形中,,,,
在和中,
,
(),
,
在和中,
,
(),
,
,
,
,
,
取的中点,连接、,
则,
在中,,
根据三角形的三边关系,>,
当、、三点共线时,的长度最小,
最小值.
故答案为:.
【点睛】本题主要考查了圆的综合题,需要掌握圆周角定理、等腰直角三角形的性质以及勾股定理等知识,难度偏大,解题时,注意辅助线的作法.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.解一元二次方程,配方后正确的是( )
A. B. C. D.
2.若九年级五名男生的体重(单位:kg)分别为50,53,51,55,55,则这五位男生体重的中位数、众数分别是( )
A.53和52 B.53和55 C.55和53 D.51和55
3.已知是关于x的一元二次方程的一个根,则m的值是( )
A. B. C.1 D.2
4.一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是( )
A.4 B.5 C.6 D.8
5.二次三项式-4x+7配方的结果是( )
A.+7 B.+3 C.+3 D.-1
6.如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为( )
A.5﹣4 B.﹣1 C.6﹣2 D.
7.某班45名同学某天每人的生活费用统计如表:
生活费(元) 10 15 20 25 30
学生人数(人) 4 10 15 10 6
对于这45名同学这天每人的生活费用,下列说法错误的是( )
A.平均数是20 B.众数是20 C.中位数是20 D.极差是20
8.如图,已知直线交于两点,是的直径,点C为上一点,且平分,过C作,垂足为D,且,的直径为,则的长等于( )
A.8 B. C. D.
二、填空题
9.方程的根为 .
10.一元二次方程的一个根为,则b的值为 .
11.如图,半圆的直径,弦,的长为,则的长为 .
12.若扇形的半径为,扇形的面积为,则该扇形的圆心角为 ,弧长为 .
13.已知一组数据,,,……,,的方差是m,那么另一组数据,,,……,的方差是 .(用含有m的代数式表示)
14.如图,在边长为6的菱形OABC中,∠AOC=60°,以顶点O为圆心、对角线OB的长为半径作弧,与射线OA,OC分别交于点D,E,则图中阴影部分的面积为 .
15.如图,从一块半径为1米的圆形铁皮圆O上剪出一个圆心角为90度的扇形,且点A、B、C都在圆上,则此时扇形的面积(保留)是 平方米.
16.AC是⊙O的直径,弦BD⊥AC于点E,连接BC,过点O作OF⊥BC于点F,若BD=12cm,OE=cm,则OF= cm.
17.如图,△ABC中,若AC=4,BC=3,AB=5,则△ABC的内切圆半径是 .
18.已知:如图,在中,弦、相交于点,,,,则 .
三、解答题
19.解方程:
(1)
(2);
20.如今网上购物已经成为一种时尚,某网店“双十一”全天交易额逐年增长,2015年交易额为40万元,2017年交易额为48.4万元,求2015年至2017年“双十一”交易额的年平均增长率?
21.某新能源汽车区域销售部希望确定一个适当的季度目标,对完成目标的员工进行奖励,以调动员工的积极性.现对名员工某季度的销售额进行统计和分析.
数据收集(单位:万元):.
数据整理:
销售额/万元
频数
数据分析:
平均数 众数 中位数
问题解决:
(1)填空:______,______.
(2)若将万元作为销售目标,则有______名员工获得奖励.
(3)销售部对数据分析后,最终对一半的员工进行了奖励.员工甲反应:“我这个季度的销售额是万元,比平均数万元高,所以我的销售额超过了一半的员工,为什么我没有拿到奖励?”请你从数学的角度给出合理的回复.
22.如图,的内接四边形中两组对边的延长线分别相交于点,且,求的度数.
23.如图,为的直径,点C,D为圆上两点,,且有平分,过C作于E.
(1)求证:为的切线
(2)若,求半径.
24.某商场统计了某品牌商品2月份到4月份的销量,该品牌商品2月份销售100件,4月份销售144件,且从2月份到4月份销售量的月增长率相同.
(1)求该品牌商品销售量的月增长率;
(2)若此种商品的进价为每件30元,销售过程中发现,当售价为每件40元时,月销售量为200件,若在此基础上每件售价上涨1元,则月销售量将减少5件,为使月销售利润达到2625元,而且尽可能让顾客得到实惠,则该品牌商品的实际售价应定为每件多少元?
25.如图,在以为直径的中,弦于点H,与弦交于点F,连接,已知,.
(1)求的半径;
(2)若,求的长.
26.如图,已知,交于点B,.
(1)求的度数;
(2)求弧的度数.
27.(1)【学习心得】
小刘同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.
例如:如图1,在中,,,是外一点,且,求的度数.若以点为圆心,为半径作辅助,则点必在上,是的圆心角,而是圆周角,从而可容易得到________.
(2)【问题解决】
如图2,在四边形中,,,求的度数.
(3)【问题拓展】
如图3,如图,是正方形的边上两个动点,满足.连接交于点,连接交于点.若正方形的边长为4,则线段长度的最小值是_________.
参考答案:
题号 1 2 3 4 5 6 7 8
答案 C B D C B A A B
1.C
【分析】题考查了用配方法解一元二次方程,解本题的关键在熟练掌握用配方法解一元二次方程的方法.配方法解一元二次方程的方法:将常数项移至方程的右边,然后两边都加上一次项系数的一半的平方配方成完全平方后,再开方.
【详解】解:
,
故选C.
2.B
【分析】中位数是按顺序排列的一组数据中居于中间位置的数,众数是一组数据中出现次数最多的数值.
【详解】解:将这组数据重新排列为50、51、53、55、55,
所以这组数据的中位数为53,众数为55,
故选:B.
【点睛】本题考查中位数、众数的求解.掌握各自定义是解题关键.
3.D
【分析】将代入求解即可.
【详解】解:∵是关于x的一元二次方程的一个根,
∴,
∴,
故选:D.
【点睛】此题考查了一元二次方程的根的定义,熟记定义是解题的关键.
4.C
【分析】根据垂径定理得出BC=AB,再根据勾股定理求出OC的长.
【详解】∵OC⊥AB,AB=16,
∴BC=AB=8.
在Rt△BOC中,OB=10,BC=8,
∴.
故选C.
5.B
【详解】把二次三项式-4x+7配方为:
.
故选B.
6.A
【分析】作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,根据两点之间线段最短得到此时PM+PN最小,再利用对称确定A′的坐标,接着利用两点间的距离公式计算出A′B的长,然后用A′B的长减去两个圆的半径即可得到MN的长,即得到+PN的最小值.
【详解】作⊙A关于x轴的对称⊙A′,连接BA′分别交⊙A′和⊙B于M、N,交x轴于P,如图,
则此时PM+PN最小,
∵点A坐标(2,3),
∴点A′坐标(2,﹣3),
∵点B(3,4),
∴A′B==5,
∴MN=A′B﹣BN﹣A′M=5﹣3﹣1=5﹣4,
∴PM+PN的最小值为5﹣4.
故选A.
【点睛】本题考查了圆的综合题:掌握与圆有关的性质和关于x轴对称的点的坐标特征;会利用两点之间线段最短解决线段和的最小值问题;会运用两点间的距离公式计算线段的长;理解坐标与图形性质.
7.A
【详解】试题分析:根据众数、中位数、极差、平均数的概念求解.
解:这组数据中位数是20,
则众数为:20,
平均数为:20.4,
极差为:30﹣10=20.
故选A.
考点:众数;加权平均数;中位数;极差.
8.B
【分析】连接,根据题意可证得,再根据角平分线的性质,得,过O作,则,得四边形为矩形,设,在中,由勾股定理得,从而求得x的值,由勾股定理得出的长.
【详解】连接,过O作,垂足为F,
,
,
平分,
,
,
,
,
,
四边形为矩形,
.
,
设,则,
的直径为,
,
,
在中,由勾股定理得.
即,
解得.
,故舍去,
,
,
,由垂径定理知,F为的中点,
.
故选:B.
【点睛】本题主要考查角平分线的性质,勾股定理、矩形的判定和性质以及垂径定理,做辅助线构建矩形是解题的关键.
9.,
【分析】本题考查了因式分解法解一元二次方程.熟练掌握因式分解法解一元二次方程是解题的关键.
利用因式分解法解一元二次方程即可.
【详解】解:,
,
,
∴,,
解得,,,
故答案为:,.
10.2022
【分析】将x=1代入原方程即可求解.
【详解】将x=1代入原方程得:1+b-2023=0,解得:b=2022;
故答案为:2022.
【点睛】本题主要考查了一元二次方程的根,掌握一元二次方程的根的定义是解题的关键.
11.
【分析】由题意可知:是等边三角形,从而可求出弧的长度,再求出半圆弧的长度后,即可求出弧的长度.
【详解】解:连接、,
,
是等边三角形,
,
的长,
又半圆弧的长度为:,
.
故答案为:
【点睛】本题考查圆了弧长的计算,等边三角形的性质等知识,属于中等题型.
12. /
【分析】本题主要考查了求扇形圆心角度数,求扇形弧长,设该扇形圆心角为,根据扇形面积公式得到,解得,再由弧长计算公式进行求解即可.
【详解】解:设该扇形圆心角为,
由题意得,,
解得,
∴该扇形圆心角为,
∴该扇形的弧长为,
故答案为:;.
13.m
【分析】根据方差的性质,直接求解即可.
【详解】解:∵数据,,,……,的方差是m,
∴由于另一组数据,,,……,是在原数据基础上每个数据都减去3,
∴新数据的波动幅度没有发生改变,
∴另一组数据,,,……,的方差是m,
故答案是:m.
【点睛】本题主要考查方差,解题的关键是掌握方差的性质:在原来每个数据都加上或减去同一个数,数据的方差不变.
14.18π﹣18
【分析】连接AC,交OB于H,根据菱形的性质可得∠COH∠AOC=30°,AC=2CH,OB=2OH,利用含30°角的直角三角形的性质及勾股定理可求出CH、OH的长,即可求出AC和OB的长,利用阴影部分的面积=S扇形OED-S菱形OABC即可得答案.
【详解】连接AC,交OB于H,
∵四边形OABC为菱形,∠AOC=60°,
∴∠COH∠AOC=30°,AC=2CH,OB=2OH,
∴CH=3,OH3,
∴AC=6,OB=6,
∴阴影部分的面积66=18π﹣18,
故答案为18π﹣18.
【点睛】本题考查了菱形的性质及扇形面积,菱形的四条边相等,对角线互相垂直且平分对角;熟练掌握菱形的性质及扇形的面积公式是解题关键.
15.
【分析】连接,先根据圆周角定理可得是的直径,再利用勾股定理可得,然后利用扇形的面积公式求解即可得.
【详解】解:如图,连接,
由题意得:,,
是的直径,
米,
,
,
则此时扇形的面积是(平方米),
故答案为:.
【点睛】本题考查了圆周角定理、扇形的面积、勾股定理,熟练掌握扇形的面积公式是解题关键.
16.或
【分析】根据题意分两种情况并综合利用垂径定理和勾股定理以及圆的基本性质进行分析即可求解.
【详解】解:如图,连接BO
∵AC是⊙O的直径,弦BD⊥AC于点E,BD=12cm,
∴,
∵OE=cm,BD⊥AC,
∴cm,
∴,,
∵OF⊥BC,
∴,
∴,
如图,
∵OE=cm,BD⊥AC, ,
∴,
∵OF⊥BC,
∴,
∴.
故答案为:或.
【点睛】本题考查圆的综合问题,熟练掌握并利用垂径定理和勾股定理以及圆的基本性质进行分析是解题的关键.注意未作图题一般情况下要进行分类作图讨论.
17.1
【分析】先利用勾股定理的逆定理得到△ABC为直角三角形,∠ACB=90°,然后利用△ABC的内切圆半径R=进行计算.
【详解】∵AC=4,BC=3,AB=5,
∴AC2+BC2=AB2,
∴△ABC为直角三角形,∠ACB=90°,
∴△ABC的内切圆半径R==1.
故答案为:1.
【点睛】本题考查了三角形内切圆与内心:与三角形各边都相切的圆叫三角形的内切圆,三角形的内切圆的圆心叫做三角形的内心.也考查了勾股定理的逆定理.
18.7
【分析】连结AC、DB,证△ACP∽△DBP,根据相似三角形对应成比例得到PD的长,进而得到CD的长.
【详解】如图,连结AC、DB,
根据同弧所对的圆周角相等,得到∠ACP=∠DBP,
又因为∠APC=∠DPB,
因此△ACP∽△DBP,
故PA:PC=PD:PB,
因此PD=4,
故CD=PC+PD =7.
【点睛】本题主要考查同弧所对的圆周角相等以及相似三角形的判定和性质,熟练掌握并活用这些知识点是解答此题的关键.
19.(1)
(2),;
【分析】(1)根据配方法解一元二次方程,即可求解;
(2)先化为整式方程,解方程即可求解,最后要检验.
【详解】(1)解:,
∴,
∴,
∴,
解得:;
(2)解:,
∴,,,
∴,
∴,
∴,;
【点睛】本题考查了解一元二次方程,解分式方程,正确的计算是解题的关键.
20.2015年至2017年“双十一”交易额的年平均增长率为10%.
【分析】设2015年至2017年“双十一”交易额的年平均增长率为x,根据2015年及2017年该网店“双十一”全天交易额,即可得出关于x的一元二次方程,解之取其正值即可得出结论.
【详解】解:设2015年至2017年“双十一”交易额的年平均增长率为x,
根据题意得:40(1+x)2=48.4,
解得:x1=0.1=10%,x2=﹣2.1.
答:2015年至2017年“双十一”交易额的年平均增长率为10%.
【点睛】考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
21.(1),;
(2);
(3)见解析.
【分析】()利用频数和中位数的定义解答即可;
()利用表格一的信息解答即可;
()利用中位数的定义解答即可;
本题考查了数据与统计,数据的分析与整理,平均数,众数,中位数与频数,熟练掌握上述数据的特征是解题的关键.
【详解】(1)解:,
将个数据按由大到小的顺序排列如下: , 位置在中间的两个数为,它们的平均数为,
∴这组数据的中位数为,
∴,
故答案为:,;
(2)解:由个数据可知,不低于万元的个数为,
∴若将月销售额不低于万元确定为销售目标,则有名员工获得奖励,
故答案为:;
(3)解:由()可知,名员工的销售额的中位数为万元,
∴名员工的销售额有一半的人,即人超过万元,
公司对一半的员工进行了奖励,说明销售额在万元及以上的人才能获得,
而员工甲的销售额是万元,低于万元,
∴员工甲不能拿到奖励.
22..
【分析】本题考查了圆内接四边形的性质,三角形的外角性质,三角形内角和定理,熟练掌握其性质是解题的关键.先根据三角形外角性质计算出,再根据圆内接四边形的性质计算出,然后再根据三角形外角性质求.
【详解】,
,
为圆内接四边形
,
,
,
.
23.(1)见解析
(2)
【分析】(1)如图:连接,由角平分线的定义及等腰三角形的性质可得,即可得,进而得到即可证明结论;
(2)如图∶连接,过C作于F.根据角平分线的性质定理可得,由圆周角定理可得,再由勾股定理可得;设半径为R,则在中运用勾股定理列关于R的方程求解即可.
【详解】(1)证明:如图:连接,
∵平分,
∴,
∵,
∴,
∴,
∴,
∴,
∵,即,
∴,即,
∵是半径,
∴为的切线.
(2)解:如图∶连接,过C作于F.
∵平分,,
∴,
∵,
∴,
∴
设半径为R,则在中,,
∴,解得:.
【点睛】本题主要考查了切线的判定、圆周角定理、等腰三角形的性质、角平分线的性质定理、勾股定理等知识点,灵活运用相关性质定理成为解题的关键.
24.(1)该品牌商品销售量的月增长率是;
(2)该品牌商品的实际售价应定为每件元.
【分析】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键.
(1)设该品牌商品销售量的月增长率为,根据该品牌商品2月份及4月份的销售量,即可得出关于的一元二次方程,解之取其正值即可得出结论;
(2)设该品牌商品的实际售价应定为每件元,则每件的销售利润为元,月销售量为件,根据月销售利润每件的销售利润月销售量,即可得出关于的一元二次方程,解之取其较小值即可得出结论.
【详解】(1)解:设该品牌商品销售量的月增长率为,依题意,得:
,
解得:,(不合题意,舍去),
答:该品牌商品销售量的月增长率为;
(2)解:设该品牌商品的实际售价应定为每件元,则每件的销售利润为元,月销售量为件,依题意,得:
,
整理得:,
解得:,,
∵尽可能让顾客得到实惠,
,
答:该品牌商品的实际售价应定为每件元.
25.(1)5
(2)6
【分析】本题考查了垂径定理、勾股定理,熟练掌握以上知识点,添加适当的辅助线是解此题的关键.
(1)连接,设半径,由垂径定理可得,从而得到,由勾股定理进行计算即可得出答案;
(2)由(1)得:直径,,,证明出,从而得到,最后由勾股定理计算即可.
【详解】(1)解:如图,连接,
设半径,
,,,是的直径,
,,
,
解得,
的半径为;
(2)解:由(1)得:直径,,,
∵
∴,
,
,
.
26.(1)
(2)
【分析】本题考查了圆心角、弧、弦的关系,等腰三角形的性质,三角形外角的性质,关键是根据三角形内角和定理和三角形外角的性质解答.
(1)连接,由,则,于是,而,得,由,根据,即可得到的度数.
(2)由(1)得,由平角的定义得的度数,从而可求出弧的度数.
【详解】(1)解:连接,如图,
∵,,
∴,
∴,
∴,
而,得,
∴,
而,
∴,
∴.
(2)解:由(1)得,,
又,
∴
∴弧的度数为.
27.(1);(2);(3)
【分析】(1)利用同弧所对的圆周角是所对圆心角的一半求解.
(2)由、、、共圆,得出,
(3)根据正方形的性质可得,,,然后利用“边角边”证明和全等,根据全等三角形对应角相等可得,利用“”证明和全等,根据全等三角形对应角相等可得,从而得到,然后求出,取的中点,连接、,根据直角三角形斜边上的中线等于斜边的一半可得,利用勾股定理列式求出,然后根据三角形的三边关系可知当、、三点共线时,的长度最小.
【详解】解:(1)如图1,
,,
以点为圆心,点、、必在上,
是的圆心角,而是圆周角,
,
故答案是:;
(2)如图2,取的中点,连接、.
,
点、、、共圆,
,
,
,
(3)如图3,在正方形中,,,,
在和中,
,
(),
,
在和中,
,
(),
,
,
,
,
,
取的中点,连接、,
则,
在中,,
根据三角形的三边关系,>,
当、、三点共线时,的长度最小,
最小值.
故答案为:.
【点睛】本题主要考查了圆的综合题,需要掌握圆周角定理、等腰直角三角形的性质以及勾股定理等知识,难度偏大,解题时,注意辅助线的作法.
同课章节目录
