福建省厦门2024-2025学年上学期八年级阶段考试数学试题(无答案)
文档属性
| 名称 | 福建省厦门2024-2025学年上学期八年级阶段考试数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 819.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 16:06:41 | ||
图片预览

文档简介
2024-2025学年第一学期八年级阶段考试
数学
(试卷满分:150分 考试时间:120分钟)
班级:_________姓名:_________座号:_________考号:_________注意事项:
1.全卷三大题,25小题,试卷共6页,另有答题卡.
2.答案一律写在答题卡上,否则不能得分.一、选择题(本大题共10小题,每小题4分,共40分.每小题只有一个选项符合题意)
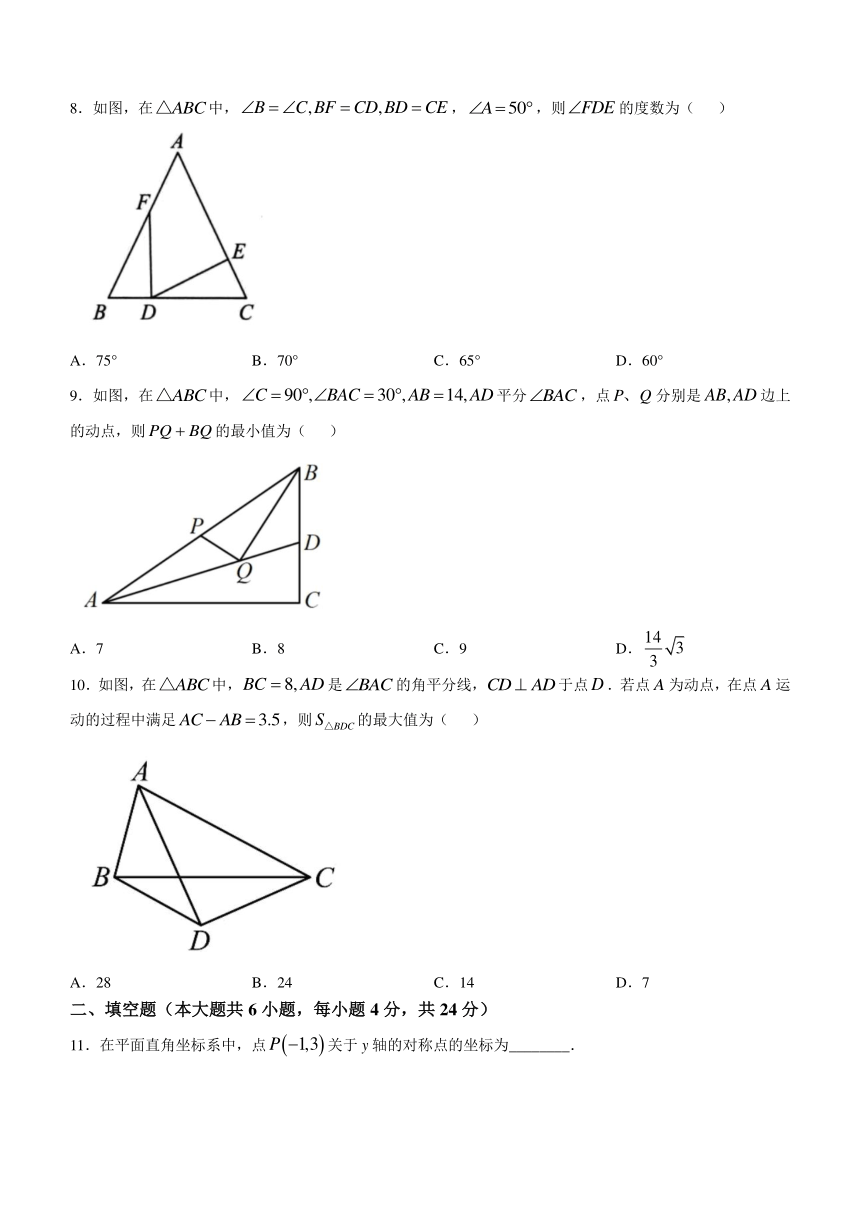
1.下列图形中,是轴对称图形的是( )
A. B. C. D.
2.一木工将一根长100厘米的木条锯成40厘米与60厘米,要另找一根木条,钉成一个三角形木架,应选择下列哪一根( )
A.10厘米 B.30厘米 C.100厘米 D.110厘米
3.下列运算正确的是( )
A. B. C. D.
4.如图,在中,是的中线,则与的周长之差为( )
A.0 B.1 C.2 D.3
5.已知图中的两个三角形全等,则等于( )
A.50° B.72° C.60° D.58°
6.一个多边形的每一个外角都等于72°,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
7.已知,则的值为( )
A. B.4 C. D.5
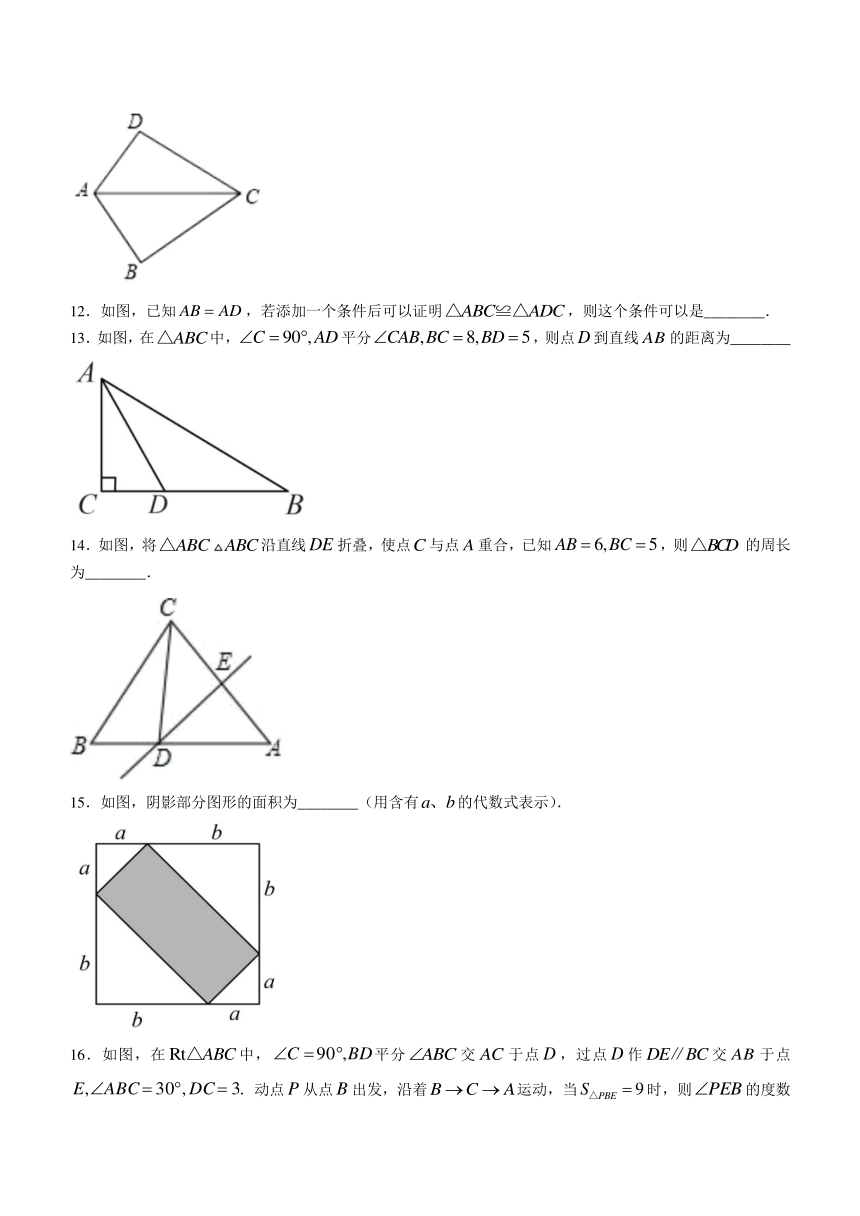
8.如图,在中,,,则的度数为( )
A.75° B.70° C.65° D.60°
9.如图,在中,平分,点分别是边上的动点,则的最小值为( )
A.7 B.8 C.9 D.
10.如图,在中,是的角平分线,于点.若点为动点,在点运动的过程中满足,则的最大值为( )
A.28 B.24 C.14 D.7
二、填空题(本大题共6小题,每小题4分,共24分)
11.在平面直角坐标系中,点关于轴的对称点的坐标为________.
12.如图,已知,若添加一个条件后可以证明,则这个条件可以是________.
13.如图,在中,平分,则点到直线的距离为________
14.如图,将沿直线折叠,使点与点重合,已知,则的周长为________.
15.如图,阴影部分图形的面积为________(用含有的代数式表示).
16.如图,在中,平分交于点,过点作交于点.动点从点出发,沿着运动,当时,则的度数为________.
三、解答题(本大题共9小题,共86分)
17.(12分)计算:
(1); (2);
(3); (4).
18.(8分)如图,,求的度数.
19.(8分)先化简,再求值:.其中.
20.(8分)如图,在中,.
(1)作线段的垂直平分线,交斜边于点(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若,求的长.
21.(8分)如图,在中,是的角平分线,于点,于点.
(1)求证:;
(2)已知,求的面积.
22.(8分)我们定义:如果两个多项式与的和为常数,则称与互为“对消多项式”,这个常数称为它们的“对消数”.如多项式与多项式,则与互为“对消多项式”,它们的“对消数”为3。
(1)下列各组多项式中,互为“对消多项式”的是________(填序号);
①与; ②与;
③与; ④与.
(2)多项式与(为常数)互为“对消多项式”,求它们的“对消数”.
23.(10分)阅读理解:
若满足,求的值.
解:设,
则,
,
.
解决问题:
(1)若满足,则________;
(2)若满足,求的值;
(3)如图,在长方形中,,点是上的点,且,分别以为边在长方形外侧作正方形和正方形CEMN,若长方形CEPF的面积为80,则图中阴影部分的面积和为多少?
24.(12分)已知是等边三角形,点是直线上一点,以点为顶点作.过点作,交射线于点,求证:.当点为的中点时,如图1,小明同学很快就证明了结论,他的做法是:取的中点,连接,然后证明,从而得到.
图1 图2 图3
(1)请完整写出小明同学的证明过程;
(2)如图2,当点为线段上的任意一点时,求证:;
(3)当点在的延长线上,且满足(其他条件不变)时,若,直接写出四边形的面积.
25.(12分)如图,在平面直角坐标系中,已知点分别在坐标轴的正半轴上.
图1 图2 图3
(1)如图1,以点为直角顶点,为直角边在第一象限内作等腰直角,若,求点的坐标;
(2)如图2,若,点是的延长线上一点(不与点重合),以点为直角顶点,为直角边在第一象限作等腰直角,,若点为点关于轴的对称点,判断点与直线的关系,并证明;
(3)如图3,在(2)的条件下,已知,连接交于点,当平分时,求线段的长(用含有的代数式表示).
数学
(试卷满分:150分 考试时间:120分钟)
班级:_________姓名:_________座号:_________考号:_________注意事项:
1.全卷三大题,25小题,试卷共6页,另有答题卡.
2.答案一律写在答题卡上,否则不能得分.一、选择题(本大题共10小题,每小题4分,共40分.每小题只有一个选项符合题意)
1.下列图形中,是轴对称图形的是( )
A. B. C. D.
2.一木工将一根长100厘米的木条锯成40厘米与60厘米,要另找一根木条,钉成一个三角形木架,应选择下列哪一根( )
A.10厘米 B.30厘米 C.100厘米 D.110厘米
3.下列运算正确的是( )
A. B. C. D.
4.如图,在中,是的中线,则与的周长之差为( )
A.0 B.1 C.2 D.3
5.已知图中的两个三角形全等,则等于( )
A.50° B.72° C.60° D.58°
6.一个多边形的每一个外角都等于72°,则这个多边形的边数为( )
A.4 B.5 C.6 D.7
7.已知,则的值为( )
A. B.4 C. D.5
8.如图,在中,,,则的度数为( )
A.75° B.70° C.65° D.60°
9.如图,在中,平分,点分别是边上的动点,则的最小值为( )
A.7 B.8 C.9 D.
10.如图,在中,是的角平分线,于点.若点为动点,在点运动的过程中满足,则的最大值为( )
A.28 B.24 C.14 D.7
二、填空题(本大题共6小题,每小题4分,共24分)
11.在平面直角坐标系中,点关于轴的对称点的坐标为________.
12.如图,已知,若添加一个条件后可以证明,则这个条件可以是________.
13.如图,在中,平分,则点到直线的距离为________
14.如图,将沿直线折叠,使点与点重合,已知,则的周长为________.
15.如图,阴影部分图形的面积为________(用含有的代数式表示).
16.如图,在中,平分交于点,过点作交于点.动点从点出发,沿着运动,当时,则的度数为________.
三、解答题(本大题共9小题,共86分)
17.(12分)计算:
(1); (2);
(3); (4).
18.(8分)如图,,求的度数.
19.(8分)先化简,再求值:.其中.
20.(8分)如图,在中,.
(1)作线段的垂直平分线,交斜边于点(要求:尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若,求的长.
21.(8分)如图,在中,是的角平分线,于点,于点.
(1)求证:;
(2)已知,求的面积.
22.(8分)我们定义:如果两个多项式与的和为常数,则称与互为“对消多项式”,这个常数称为它们的“对消数”.如多项式与多项式,则与互为“对消多项式”,它们的“对消数”为3。
(1)下列各组多项式中,互为“对消多项式”的是________(填序号);
①与; ②与;
③与; ④与.
(2)多项式与(为常数)互为“对消多项式”,求它们的“对消数”.
23.(10分)阅读理解:
若满足,求的值.
解:设,
则,
,
.
解决问题:
(1)若满足,则________;
(2)若满足,求的值;
(3)如图,在长方形中,,点是上的点,且,分别以为边在长方形外侧作正方形和正方形CEMN,若长方形CEPF的面积为80,则图中阴影部分的面积和为多少?
24.(12分)已知是等边三角形,点是直线上一点,以点为顶点作.过点作,交射线于点,求证:.当点为的中点时,如图1,小明同学很快就证明了结论,他的做法是:取的中点,连接,然后证明,从而得到.
图1 图2 图3
(1)请完整写出小明同学的证明过程;
(2)如图2,当点为线段上的任意一点时,求证:;
(3)当点在的延长线上,且满足(其他条件不变)时,若,直接写出四边形的面积.
25.(12分)如图,在平面直角坐标系中,已知点分别在坐标轴的正半轴上.
图1 图2 图3
(1)如图1,以点为直角顶点,为直角边在第一象限内作等腰直角,若,求点的坐标;
(2)如图2,若,点是的延长线上一点(不与点重合),以点为直角顶点,为直角边在第一象限作等腰直角,,若点为点关于轴的对称点,判断点与直线的关系,并证明;
(3)如图3,在(2)的条件下,已知,连接交于点,当平分时,求线段的长(用含有的代数式表示).
同课章节目录
