第一章 特殊的平行四边形正方形 综合练习(无答案)2024—2025学年北师大版数学九年级上册
文档属性
| 名称 | 第一章 特殊的平行四边形正方形 综合练习(无答案)2024—2025学年北师大版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 79.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 16:07:47 | ||
图片预览

文档简介
第一章特殊的平行四边形正方形综合练习北师大版2024—2025学年九年级上册
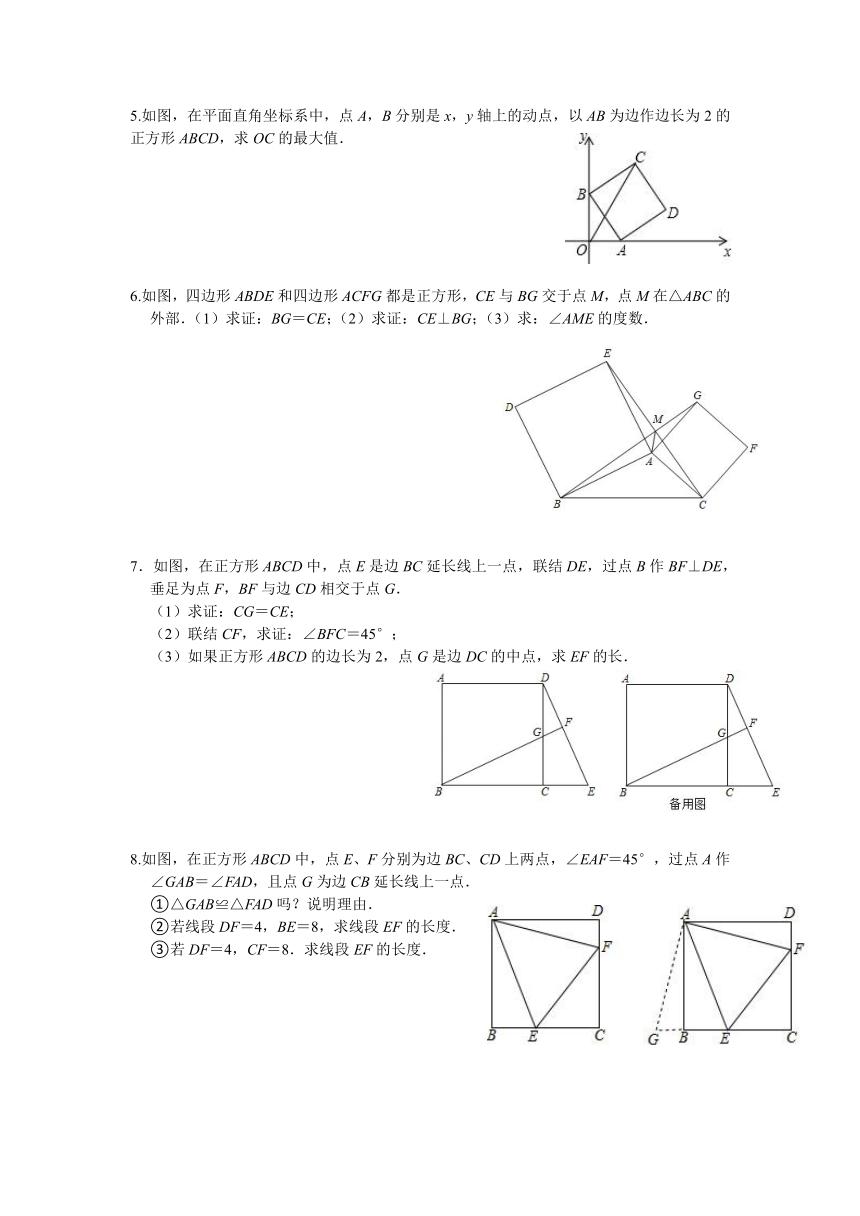
1.如图,在正方形ABCD中,点E是BC边中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)求证:AE=EF;
(2)若AB=2,求四边形AEFD的面积.
2.如图,四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)若AB=2,CE=2,求CG的长;
(3)当∠ADE=40°时,求∠EFC的度数.
3.如图,在正方形ABCD中,点E、F、G分别在CD、AD、BC上,且FG⊥BE,垂足为O.
(1)求证:BE=FG;
(2)若O是BE的中点,且BC=8,EC=3,求AF的长.
4.如图,已知正方形ABCD中,点P为对角线AC上的动点(不与A、C重合),PE⊥AB,PF⊥BC,垂足分别为E、F,连接PD、EF.
(1)求证:EF=PD;
(2)若PD=13,PF=5,求对角线AC的长.
5.如图,在平面直角坐标系中,点A,B分别是x,y轴上的动点,以AB为边作边长为2的正方形ABCD,求OC的最大值.
6.如图,四边形ABDE和四边形ACFG都是正方形,CE与BG交于点M,点M在△ABC的外部.(1)求证:BG=CE;(2)求证:CE⊥BG;(3)求:∠AME的度数.
7.如图,在正方形ABCD中,点E是边BC延长线上一点,联结DE,过点B作BF⊥DE,垂足为点F,BF与边CD相交于点G.
(1)求证:CG=CE;
(2)联结CF,求证:∠BFC=45°;
(3)如果正方形ABCD的边长为2,点G是边DC的中点,求EF的长.
8.如图,在正方形ABCD中,点E、F分别为边BC、CD上两点,∠EAF=45°,过点A作∠GAB=∠FAD,且点G为边CB延长线上一点.
①△GAB≌△FAD吗?说明理由.
②若线段DF=4,BE=8,求线段EF的长度.
③若DF=4,CF=8.求线段EF的长度.
9.如图,已知正方形ABCD,∠MAN=45°,连接CB,交AM、AN分别于点P、Q,求证:CP2+BQ2=PQ2.
10.如图所示,在正方形ABCD中,AB=10,点O为对角线交点,BE=CF,连接EF,过点O作OG⊥EF交BC边于G,点G始终在BC边上,并且不与点B、点C重合,连接OE、OF、EG.
(1)求证:OE=OF;
(2)请求出∠EOG的度数?
(3)试求出△BEG的周长;
(4)若AE=AO,请直接写出四边形BEOG的面积.
11.如图,在正方形ABCD中,AC交BD于O,F在AC上,连线DF,过F作FE⊥DF交BD于G,交AB于E.
(1)求证:DF=EF;
(2)若F为OC中点,求证:FG=EG.
12.已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图①,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F,若DF⊥CE,求证:OE=OG;
(2)如图②,若CE平分∠BCO,DH⊥CE于点F,交BC于点H,交AC于点G,求证:OG=BH.
13.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.
(1)求证:四边形ABCD是正方形.
(2)已知AB的长为6,求(BE+6)(DF+6)的值.
(3)借助于上面问题的解题思路,解决下列问题:若三角形PQR中,∠QPR=45°,一条高是PH,长度为6,QH=2,求HR长度.
14.如图,正方形ABCD的边长为1,E为对角线BD上一点,且BE=BC,点P为线段CE上一动点,且PM⊥BE于点M,PN⊥BC于点N,求PM+PN的值.
1.如图,在正方形ABCD中,点E是BC边中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)求证:AE=EF;
(2)若AB=2,求四边形AEFD的面积.
2.如图,四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)若AB=2,CE=2,求CG的长;
(3)当∠ADE=40°时,求∠EFC的度数.
3.如图,在正方形ABCD中,点E、F、G分别在CD、AD、BC上,且FG⊥BE,垂足为O.
(1)求证:BE=FG;
(2)若O是BE的中点,且BC=8,EC=3,求AF的长.
4.如图,已知正方形ABCD中,点P为对角线AC上的动点(不与A、C重合),PE⊥AB,PF⊥BC,垂足分别为E、F,连接PD、EF.
(1)求证:EF=PD;
(2)若PD=13,PF=5,求对角线AC的长.
5.如图,在平面直角坐标系中,点A,B分别是x,y轴上的动点,以AB为边作边长为2的正方形ABCD,求OC的最大值.
6.如图,四边形ABDE和四边形ACFG都是正方形,CE与BG交于点M,点M在△ABC的外部.(1)求证:BG=CE;(2)求证:CE⊥BG;(3)求:∠AME的度数.
7.如图,在正方形ABCD中,点E是边BC延长线上一点,联结DE,过点B作BF⊥DE,垂足为点F,BF与边CD相交于点G.
(1)求证:CG=CE;
(2)联结CF,求证:∠BFC=45°;
(3)如果正方形ABCD的边长为2,点G是边DC的中点,求EF的长.
8.如图,在正方形ABCD中,点E、F分别为边BC、CD上两点,∠EAF=45°,过点A作∠GAB=∠FAD,且点G为边CB延长线上一点.
①△GAB≌△FAD吗?说明理由.
②若线段DF=4,BE=8,求线段EF的长度.
③若DF=4,CF=8.求线段EF的长度.
9.如图,已知正方形ABCD,∠MAN=45°,连接CB,交AM、AN分别于点P、Q,求证:CP2+BQ2=PQ2.
10.如图所示,在正方形ABCD中,AB=10,点O为对角线交点,BE=CF,连接EF,过点O作OG⊥EF交BC边于G,点G始终在BC边上,并且不与点B、点C重合,连接OE、OF、EG.
(1)求证:OE=OF;
(2)请求出∠EOG的度数?
(3)试求出△BEG的周长;
(4)若AE=AO,请直接写出四边形BEOG的面积.
11.如图,在正方形ABCD中,AC交BD于O,F在AC上,连线DF,过F作FE⊥DF交BD于G,交AB于E.
(1)求证:DF=EF;
(2)若F为OC中点,求证:FG=EG.
12.已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图①,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F,若DF⊥CE,求证:OE=OG;
(2)如图②,若CE平分∠BCO,DH⊥CE于点F,交BC于点H,交AC于点G,求证:OG=BH.
13.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.
(1)求证:四边形ABCD是正方形.
(2)已知AB的长为6,求(BE+6)(DF+6)的值.
(3)借助于上面问题的解题思路,解决下列问题:若三角形PQR中,∠QPR=45°,一条高是PH,长度为6,QH=2,求HR长度.
14.如图,正方形ABCD的边长为1,E为对角线BD上一点,且BE=BC,点P为线段CE上一动点,且PM⊥BE于点M,PN⊥BC于点N,求PM+PN的值.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
