一次函数
图片预览




文档简介
课件12张PPT。一次函数1、一次函数解析式的特征是什么?
2、一次函数与正比例函数解析式的区别和联系分别是什么?
3、这种区别反映在图象上还有什么特点?
4、如何画正比例函数和一次函数y=kx+b的图象?
5、对于一次函数y=kx+b ,当b=0时,它的图象是一条直线。那么当k=0时,它的图象又是什么形状?
6、一般地,一次函数的图象是一条直线,而在实际问题中函数的图象又如何呢?挑战自我 1、已知一次函数y=(m-1)x+2m-1的图象经过原点,(1) 求m。
(2)若图象经过(2,7),求m。
(3)函数的图象平行于直线y=2x。
(4)沿y轴平移几个单位得到直线y=3x-2。
(5)函数y随x增大而减小?
(6)函数的图象交y轴正半轴?
(7)函数的图象不经过第一象限?巩固练习 2、甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价八折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价八五折优惠。设顾客预计累计购物x元(x>300)
(1)请用含x的代数式分别表示顾客在两家超市购物所付的费用。
(2)试比较顾客到哪家超市购物更优惠?说明你的理由。
解:设顾客在甲超市购物所付的费用为y1元,在乙超市购物所付的费用为y2元。
Y1=300+0.8(x-300) =(0.8x+60)元
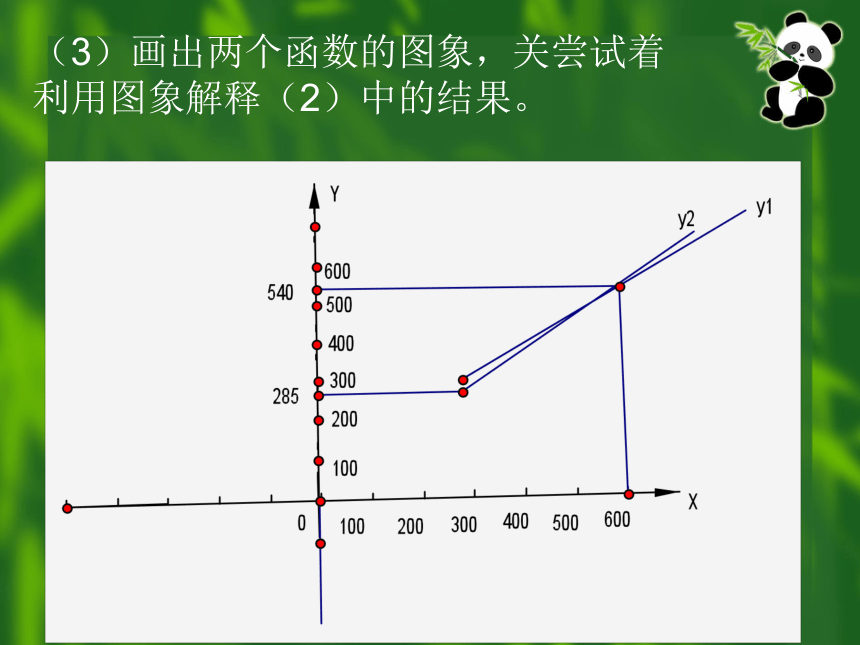
Y2=200+0.85(x-200) =(0.85x+30)元当y1=y2时,即0.8x+60=0.85x+30,解得x=600,
当y1>y2时,即0.8x+60>0.85x+30,解得x<600,
当y1<y2时,即0.8x+60<0.85x+30,解得x>600,
走进中招(06河南)(3)画出两个函数的图象,关尝试着
利用图象解释(2)中的结果。
3、已知一次函数y=kx+b,当0≤x≤2时,对应的y值3≤y≤4.
(1)试求这个一次函数的解析式。
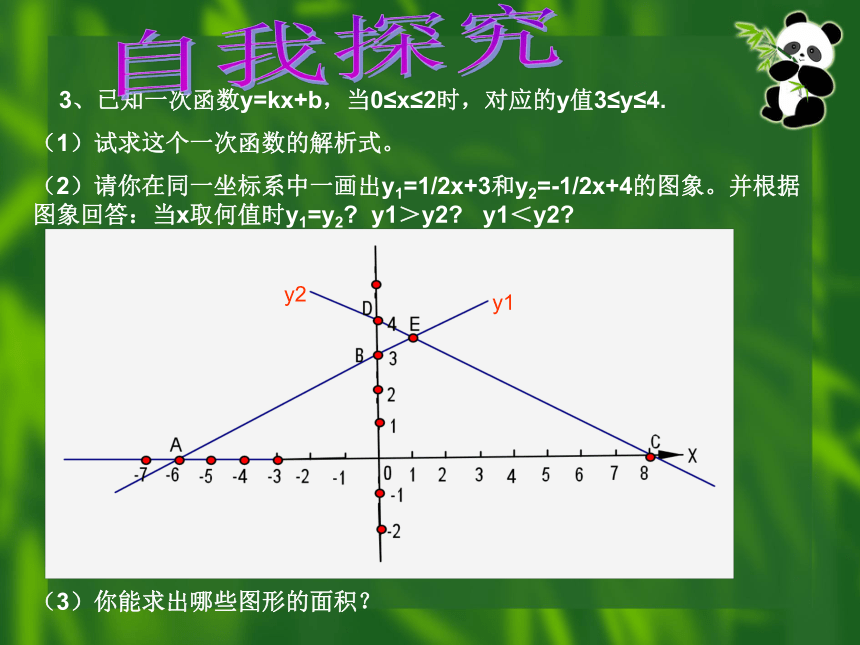
(2)请你在同一坐标系中一画出y1=1/2x+3和y2=-1/2x+4的图象。并根据图象回答:当x取何值时y1=y2? y1>y2? y1<y2?
(3)你能求出哪些图形的面积?自我探究(4)过E点能否作一条直线将AEC的面积分为1:6的两部分。试写出直线与X轴的交点坐标。(5)翻折直线AB得到(沿X轴翻)直线AF。再将直线AB沿X轴平移得到直线CF。试判断四边形AECF的形状,并说明理由。小结:
1、一次函数的图象和性质;
2、利用一次函数的性质解决实际问题;
3、要注意从不同的角度思考问题,挖掘知识间的联系;
4、本节课体现的数学思想:分类讨论、转化、数形结合等。谢谢!再见!
2、一次函数与正比例函数解析式的区别和联系分别是什么?
3、这种区别反映在图象上还有什么特点?
4、如何画正比例函数和一次函数y=kx+b的图象?
5、对于一次函数y=kx+b ,当b=0时,它的图象是一条直线。那么当k=0时,它的图象又是什么形状?
6、一般地,一次函数的图象是一条直线,而在实际问题中函数的图象又如何呢?挑战自我 1、已知一次函数y=(m-1)x+2m-1的图象经过原点,(1) 求m。
(2)若图象经过(2,7),求m。
(3)函数的图象平行于直线y=2x。
(4)沿y轴平移几个单位得到直线y=3x-2。
(5)函数y随x增大而减小?
(6)函数的图象交y轴正半轴?
(7)函数的图象不经过第一象限?巩固练习 2、甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,各自推出不同的优惠方案:在甲超市累计购买商品超出300元之后,超出部分按原价八折优惠;在乙超市累计购买商品超出200元之后,超出部分按原价八五折优惠。设顾客预计累计购物x元(x>300)
(1)请用含x的代数式分别表示顾客在两家超市购物所付的费用。
(2)试比较顾客到哪家超市购物更优惠?说明你的理由。
解:设顾客在甲超市购物所付的费用为y1元,在乙超市购物所付的费用为y2元。
Y1=300+0.8(x-300) =(0.8x+60)元
Y2=200+0.85(x-200) =(0.85x+30)元当y1=y2时,即0.8x+60=0.85x+30,解得x=600,
当y1>y2时,即0.8x+60>0.85x+30,解得x<600,
当y1<y2时,即0.8x+60<0.85x+30,解得x>600,
走进中招(06河南)(3)画出两个函数的图象,关尝试着
利用图象解释(2)中的结果。
3、已知一次函数y=kx+b,当0≤x≤2时,对应的y值3≤y≤4.
(1)试求这个一次函数的解析式。
(2)请你在同一坐标系中一画出y1=1/2x+3和y2=-1/2x+4的图象。并根据图象回答:当x取何值时y1=y2? y1>y2? y1<y2?
(3)你能求出哪些图形的面积?自我探究(4)过E点能否作一条直线将AEC的面积分为1:6的两部分。试写出直线与X轴的交点坐标。(5)翻折直线AB得到(沿X轴翻)直线AF。再将直线AB沿X轴平移得到直线CF。试判断四边形AECF的形状,并说明理由。小结:
1、一次函数的图象和性质;
2、利用一次函数的性质解决实际问题;
3、要注意从不同的角度思考问题,挖掘知识间的联系;
4、本节课体现的数学思想:分类讨论、转化、数形结合等。谢谢!再见!
