2024-2025学年江西省九年级上学期期中专题复习第四章 图形的相似部分(含解析)
文档属性
| 名称 | 2024-2025学年江西省九年级上学期期中专题复习第四章 图形的相似部分(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 16:41:14 | ||
图片预览




文档简介
2024-2025学年度江西省九年级上学期期中专题复习
图形的相似部分
本资料以2023年江西省各大市期中考试题目汇编而成,旨在为学生期中复习理清方向!
一、单选题
1.(23-24九年级上·江西景德镇·期中)下列各组图形中,一定相似的是( )
A.两个等腰直角三角形 B.两个直角三角形
C.两个等腰三角形 D.两个锐角三角形
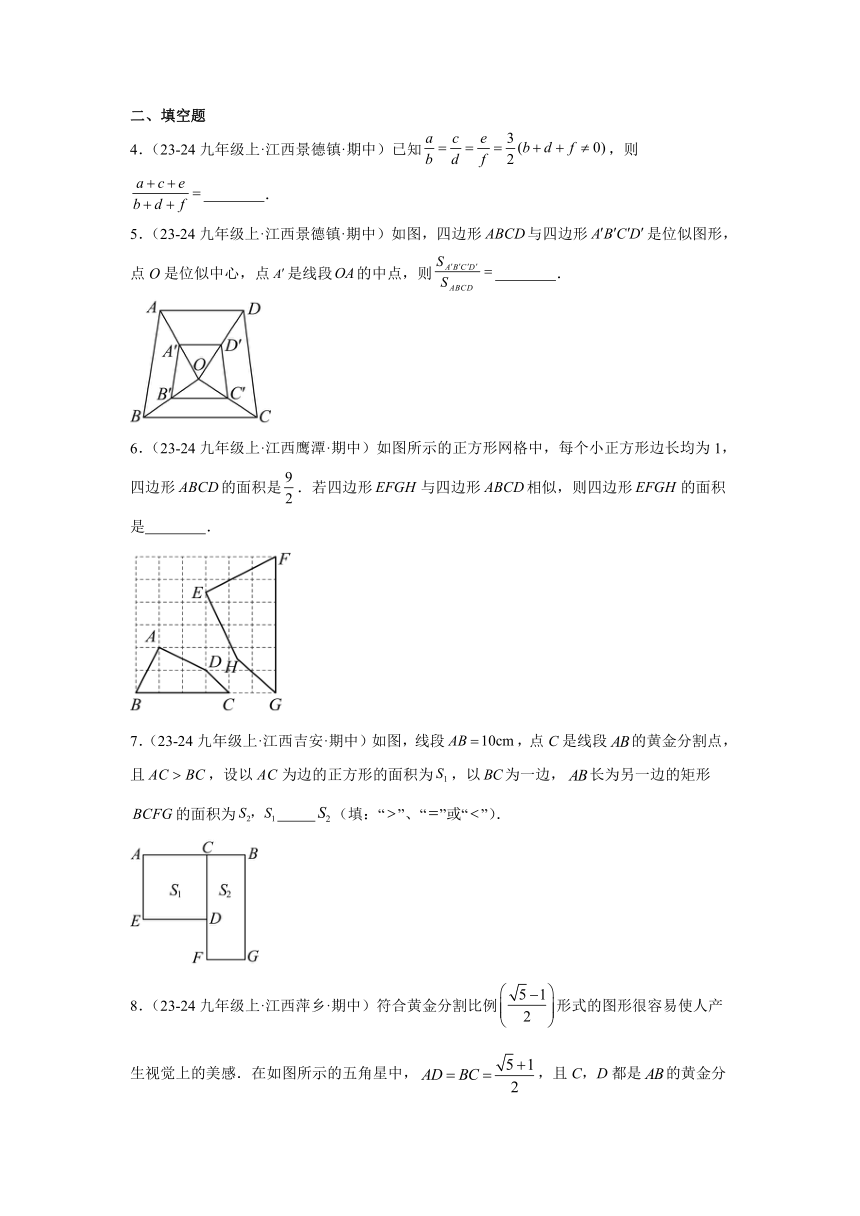
2.(23-24九年级上·江西鹰潭·期中)如图,△ABC与△DEF位似,点O是它们的位似中心,其中OE=2OB,则△ABC与△DEF的周长之比是( )
A.1:2 B.1:4 C.1:3 D.1:9
3.(23-24九年级上·江西九江·期中)如图,中,,,.将沿图中的剪开.剪下的阴影三角形与原三角形不相似的是( )
B.
C.D.
二、填空题
4.(23-24九年级上·江西景德镇·期中)已知,则 .
5.(23-24九年级上·江西景德镇·期中)如图,四边形与四边形是位似图形,点O是位似中心,点是线段的中点,则 .
6.(23-24九年级上·江西鹰潭·期中)如图所示的正方形网格中,每个小正方形边长均为1,四边形的面积是.若四边形与四边形相似,则四边形的面积是 .
7.(23-24九年级上·江西吉安·期中)如图,线段,点C是线段的黄金分割点,且,设以为边的正方形的面积为,以为一边,长为另一边的矩形的面积为 (填:“”、“”或“”).
8.(23-24九年级上·江西萍乡·期中)符合黄金分割比例形式的图形很容易使人产生视觉上的美感.在如图所示的五角星中,,且C,D都是的黄金分割点,则的长为 .
9.(23-24九年级上·江西抚州·期中)如图,,,,,,点在上移动,当与相似时,的值为 .
三、解答题
10.(23-24九年级上·江西景德镇·期中)如图,正方形中,E,F分别是边,上的点,,,连接并延长交的延长线于点G.
(1)求证:;
(2)若正方形的边长为4,求的长.
11.(23-24九年级上·江西九江·期中)如图所示,在的正方形方格中,和的顶点都在边长为的小正方形的顶点上.
(1)填空:______,______;
(2)判断与是否相似?并证明你的结论.
12.(23-24九年级上·江西鹰潭·期中)人体上半身长和下半身长的黄金比为,这时人的身长比例看上去更美观.某演员的身长情况如图所示,她想通过穿高跟鞋使身长比例更美观,于是她购买了一双6厘米的高跟鞋.请依据“黄金比”判断这双高跟鞋的高度是偏高还是偏低?
13.(23-24九年级上·江西景德镇·期中)杭州第届亚洲运动会开幕式在杭州奥体中心主体育场举行,奥运会游泳冠军汪顺和代表火炬线上传递参与者的“虚拟数字火炬手”一同点燃了杭州亚运会的主火炬台.某校社会实践小组为了测量这座主火炬台顶端距离地面的高度,如图,小明先在地面上处垂直于地面竖立了高度为米的标杆,这时地面上的点,标杆的顶端点,火炬台的顶端正好在同一直线上,测得米;小明再从点出发沿着方向前进米,到达点.在点处放置一平面镜,小刚站在处时,恰好在平面镜中看到火炬顶端的像,此时测得小刚的眼睛到地面的距离为米,米.已知点与火炬台的底端在同一直线上,,,.(平面镜大小忽略不计)
(1)求与的等量关系;
(2)请你根据以上数据,计算该火炬台的高度.
14.(23-24九年级上·江西九江·期中)如图是的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1)如图1,在边上找一点P,使得.
(2)如图2,在边上找一点Q,使得.
15.(23-24九年级上·江西吉安·期中)已知,如图所示的四边形ABCD为菱形,AC、BD交于O,AF⊥BC于F,交于点E.
(1)求证:
(2)求证:;
(3)过点E作,若,交于点G,若菱形ABCD的面积为,求的长.
16.(23-24九年级上·江西景德镇·期中)如图,在△ABC中,DE∥BC,=.
(1)如果AD=4,求BD的长度;
(2)如果S△ADE=2,求S四边形DBCE的值.
17.(23-24九年级上·江西九江·期中)如图1,在纸片中,,,,D,E分别是,边上的动点,且,连接,将沿翻折,点B落在点F的位置,连接.
(1)如图2,当点F在边上时,求的长.
(2)如图3,点在运动过程中,当时,求的长.
18.(23-24九年级上·江西景德镇·期中)如图1.已知四边形是矩形.点在的延长线上.与相交于点,与相交于点
求证:;
若,求的长;
如图2,连接,求证:.
19.(23-24九年级上·江西鹰潭·期中)如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
① 当时, ;② 当时,
(2)拓展探究
试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.
20.(23-24九年级上·江西萍乡·期中)问题背景:一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论.如图①,已知是的角平分线,可证.小慧的证明思路是:如图②,过点C作,交的延长线于点E,构造相似三角形来证明尝试证明:
(1)请参照小慧提供的思路,利用图②证明:.
应用拓展:
(2)如图③,在中,,D是边上一点,连接,将沿所在直线折叠,点C恰好落在边上的E点处.若,,求的长.
21.(23-24九年级上·江西吉安·期中)如图,在四边形ABCD中,G是DC上的点,连接BG,点F是BG上的点,在BC上取点H,使,连接HF,CF,AF.
(1)①如图1,点F为正方形ABCD中对角线AC上一点,求证:;
②如图2,在正方形ABCD中,若于F,求证:.
(2)如图3,若四边形ABCD为菱形,
①直接写出与之间的数量关系;
②若,.,,求AH的长;
22.(23-24九年级上·江西景德镇·期中)如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2,则BC= .
参考答案:
1.A
【详解】解:、任意两个等腰直角三角形,根据等腰直角三角形的性质,两腰分别相等,它们两边的比值成比例,夹角为直角相等,根据相似三角形的判定定理可得任意两个等腰直角三角形相似,故符合题意;
、任意两个直角三角形,根据三角形相似的判定定理不能得到任意两个直角三角形相似,故不符合题意;
、任意两个等腰三角形,根据三角形相似的判定定理不能得到任意两个等腰三角形相似,故不符合题意;
、任意两个锐角三角形,根据三角形相似的判定定理不能得到任意两个锐角三角形相似,故不符合题意;
故选:.
2.A
【详解】解:∵△ABC与△DEF位似,点O为位似中心.
∴△ABC∽△DEF,OB:OE= 1:2,
∴△ABC与△DEF的周长比是:1:2.
故选:A.
3.C
【详解】解:A、∵,
∴,故本选项不符合题意;
B、∵,
∴,故本选项不符合题意;
C、由图形可知,只有,不能判断,故本选项符合题意;
D、∵,
∴,故本选项不符合题意;
故选:C.
4.
【详解】解:∵,
∴,
故答案为:.
5./
【详解】解:∵点是线段的中点,
∴,
∵四边形与四边形是位似图形,
∴,
故答案为:.
6.
【详解】解:由相似多边形的性质可知,,
∴,解得,,
故答案为:.
7.
【详解】解:∵点C是线段的黄金分割点,且,
∴,
∴,
∵,
∴,
故答案为:.
8.1
【详解】解:∵C,D两点都是的黄金分割点,
∴,
,,
∴,
将,代入,
得:,
∴,
整理得:,
,
故答案为:1.
9.2或或12
【详解】解:与,,,
当与为对应边,
,
,,,
,
,
,
当与为对应边,
,
,,,
,
,
或12,
综上所述:当的值为2或或12时相似.
故答案为:2或8.4或12.
10.(1)证明见详解;
(2);
【详解】(1)证明:∵四边形是正方形,
∴,,
∵,,
∴,
∴;
(2)解:∵四边形是正方形,
∴,,
∴,
∴,
∴,
∵正方形的边长为4,,,
∴,,,
∴,
∴,
∴.
11.(1);
(2),理由见解析
【详解】(1)解:,
;
故答案为; ;
(2)解:.
证明:在的正方形方格中,
,,
.
,, ,
,.
∴
.
12.这双高跟鞋的高度偏高
【详解】解:设这双高跟鞋的高度为时,人体上半身长和下半身长成黄金比例,
由题意得:,
解得:,
,
这双高跟鞋的高度偏高.
13.(1),理由见解析;
(2)该火炬台的高度米.
【详解】(1)解:,理由:
∵点与火炬台的底端在同一直线上,,,
∴,
∴,
∴,
∵米,米,
∴,
∴;
(2)解:由题意得:米,
∴(米),
∵点与火炬台的底端在同一直线上,,,
∴,
∴,
∴,
∵米,米,
∴,即,
由()得:,
∴,
∴(米),
答:该火炬台的高度为米.
14.(1)见解析
(2)见解析
【详解】(1)如图所示,点P即为所求.
证明:由网格的特点可得,,,
∴
又∵
∴;
(2)如图所示,确定点M,然后连接连接交于点Q,点Q即为所求.
证明:由网格的特点可得,
是横4竖2的长方形的对角线,是横2竖4的长方形的对角线,
∴
∴
∴
∵
∴
又∵
∴;
15.(1)见解析
(2)见解析
(3)
【详解】(1)证明:∵对顶角相等
∴
∵菱形
∴且平分与(菱形两对角线互相垂直平分)
∵
∴
∵
∴
∴(两角对应相等的两三角形相似)
(2)由(1)得,
∴
∵菱形
∴,BD=2OD
∴即
∴,
∴(两角对应相等的两三角形相似)
∴
∴
∴.
(3)∵菱形面积为,
∴
∵D
∴
∴
设,则,BD=3m
由(2)得:
∴
在中,,
∴
此时
(舍去负值)
则
∵,
∴
∴
∴.
16.(1)BD=6;(2)S四边形DBCE=.
【详解】(1)∵DE∥BC,
∴△ADE∽△ABC,
∴=,
∵=,AD=4,
∴=,
∴BD=6;
(2)∵△ADE∽△ABC,=,
∴=()2,
∵S△ADE=2,
∴=()2,
解得:S四边形DBCE=.
17.(1)
(2)
【详解】(1)解:由翻折的性质可得: ,
∵
∴
∴四边形是菱形
∴
∴
∴
∴
在中,,,
∴
∴
设 ,则:
∵
∴
解得:
∴;
(2)解:如图,作,交于点;
∵
∴
∵四边形是菱形
∴ ,
∵
∴四边形是平行四边形
∴ ,
∴ ,
∴
在中
在中
.
18.(1)见解析;(2);(3)见解析
【详解】(1)∵四边形ABCD是矩形,
∴∠BAD=∠EAD=90 ,AO=BC,AD∥BC,
在△EAF和△DAB,
,
∴△EAF≌△DAB(SAS),
∴∠E=∠BDA,
∵∠BDA+∠ABD=90 ,
∴∠E+∠ABD=90 ,
∴∠EGB=90 ,
∴BG⊥EC;
(2)设AE=x,则EB=1+x,BC=AD=AE=x,
∵AF∥BC,∠E=∠E,
∴△EAF∽△EBC,
∴,又AF=AB=1,
∴即,
解得:,(舍去)
即AE=;
(3)在EG上截取EH=DG,连接AH,
在△EAH和△DAG,
,
∴△EAH≌△DAG(SAS),
∴∠EAH=∠DAG,AH=AG,
∵∠EAH+∠DAH=90 ,
∴∠DAG+∠DAH=90 ,
∴∠HAG=90 ,
∴△GAH是等腰直角三角形,
∴即,
∴GH=AG,
∵GH=EG-EH=EG-DG,
∴.
19.(1)①,②.(2)无变化;理由参见解析.(3),.
【详解】(1)①当α=0°时,
∵Rt△ABC中,∠B=90°,
∴AC=,
∵点D、E分别是边BC、AC的中点,
∴,BD=8÷2=4,
∴.
②如图1,
,
当α=180°时,
可得AB∥DE,
∵,
∴
(2)如图2,
,
当0°≤α<360°时,的大小没有变化,
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵,
∴△ECA∽△DCB,
∴.
(3)①如图3,
,
∵AC=4,CD=4,CD⊥AD,
∴AD=
∵AD=BC,AB=DC,∠B=90°,
∴四边形ABCD是矩形,
∴BD=AC=.
②如图4,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P,
,
∵AC=,CD=4,CD⊥AD,
∴AD=,
∵点D、E分别是边BC、AC的中点,
∴DE==2,
∴AE=AD-DE=8-2=6,
由(2),可得
,
∴BD=.
综上所述,BD的长为或.
20.(1)见解析(2)
【详解】(1)证明:∵,
∴,,
∴,
∴,
∵,,
∴,
∴,
∴.
(2)∵将沿所在直线折叠,点C恰好落在边上的E点处,
∴,,
由(1)可知,,
又∵,
∴
∴,
∵,
∴
∴,
∴,
∴;
∴.
21.(1)①见解析;②见解析
(2)①+=180°;②
【详解】(1)①∵点F为正方形ABCD中对角线AC上一点,
∴AC平分,
∴∠GCF=∠HCF
又∵,
∴,
∴;
②∵由,,,
可得,
∴,,
∵,,
∴,
∴,
∴;
(2)①+=180°,
理由:∵∠CFB=∠BCD,∠FBC=∠FBC,
∴△BFC∽ △BCG,
∴,,
又∵CG=CH,AB=BC,
∴,
∵∠ABF=∠FCB,
∴△CFH ∽△BFA,
∴∠CHF=∠FAB,
∵∠CHF+∠BHF=180°,
∴+=180°;
②由,,
得,
∴,,
又∵,,
∴,
∴,得,
∵∠CHF+∠BHF=180°,
∴+=180°,
∵,
∴,与互补,
将AH绕着点H逆时针旋转120度至,可得,
连接,可得,
∴,,
∴点A、B、共线,
∵.
∴是以120°为顶点的等腰三角形,
易得,即,
∴.
22.(1)①四边形CEGF是正方形;②;(2)线段AG与BE之间的数量关系为AG=BE;(3)3
【详解】(1)①∵四边形ABCD是正方形,
∴∠BCD=90°,∠BCA=45°,
∵GE⊥BC、GF⊥CD,
∴∠CEG=∠CFG=∠ECF=90°,
∴四边形CEGF是矩形,∠CGE=∠ECG=45°,
∴EG=EC,
∴四边形CEGF是正方形;
②由①知四边形CEGF是正方形,
∴∠CEG=∠B=90°,∠ECG=45°,
∴,GE∥AB,
∴,
故答案为;
(2)连接CG,
由旋转性质知∠BCE=∠ACG=α,
在Rt△CEG和Rt△CBA中,
=、=,
∴=,
∴△ACG∽△BCE,
∴,
∴线段AG与BE之间的数量关系为AG=BE;
(3)∵∠CEF=45°,点B、E、F三点共线,
∴∠BEC=135°,
∵△ACG∽△BCE,
∴∠AGC=∠BEC=135°,
∴∠AGH=∠CAH=45°,
∵∠CHA=∠AHG,
∴△AHG∽△CHA,
∴,
设BC=CD=AD=a,则AC=a,
则由得,
∴AH=a,
则DH=AD﹣AH=a,CH==a,
∴由得,
解得:a=3,即BC=3,
故答案为3
图形的相似部分
本资料以2023年江西省各大市期中考试题目汇编而成,旨在为学生期中复习理清方向!
一、单选题
1.(23-24九年级上·江西景德镇·期中)下列各组图形中,一定相似的是( )
A.两个等腰直角三角形 B.两个直角三角形
C.两个等腰三角形 D.两个锐角三角形
2.(23-24九年级上·江西鹰潭·期中)如图,△ABC与△DEF位似,点O是它们的位似中心,其中OE=2OB,则△ABC与△DEF的周长之比是( )
A.1:2 B.1:4 C.1:3 D.1:9
3.(23-24九年级上·江西九江·期中)如图,中,,,.将沿图中的剪开.剪下的阴影三角形与原三角形不相似的是( )
B.
C.D.
二、填空题
4.(23-24九年级上·江西景德镇·期中)已知,则 .
5.(23-24九年级上·江西景德镇·期中)如图,四边形与四边形是位似图形,点O是位似中心,点是线段的中点,则 .
6.(23-24九年级上·江西鹰潭·期中)如图所示的正方形网格中,每个小正方形边长均为1,四边形的面积是.若四边形与四边形相似,则四边形的面积是 .
7.(23-24九年级上·江西吉安·期中)如图,线段,点C是线段的黄金分割点,且,设以为边的正方形的面积为,以为一边,长为另一边的矩形的面积为 (填:“”、“”或“”).
8.(23-24九年级上·江西萍乡·期中)符合黄金分割比例形式的图形很容易使人产生视觉上的美感.在如图所示的五角星中,,且C,D都是的黄金分割点,则的长为 .
9.(23-24九年级上·江西抚州·期中)如图,,,,,,点在上移动,当与相似时,的值为 .
三、解答题
10.(23-24九年级上·江西景德镇·期中)如图,正方形中,E,F分别是边,上的点,,,连接并延长交的延长线于点G.
(1)求证:;
(2)若正方形的边长为4,求的长.
11.(23-24九年级上·江西九江·期中)如图所示,在的正方形方格中,和的顶点都在边长为的小正方形的顶点上.
(1)填空:______,______;
(2)判断与是否相似?并证明你的结论.
12.(23-24九年级上·江西鹰潭·期中)人体上半身长和下半身长的黄金比为,这时人的身长比例看上去更美观.某演员的身长情况如图所示,她想通过穿高跟鞋使身长比例更美观,于是她购买了一双6厘米的高跟鞋.请依据“黄金比”判断这双高跟鞋的高度是偏高还是偏低?
13.(23-24九年级上·江西景德镇·期中)杭州第届亚洲运动会开幕式在杭州奥体中心主体育场举行,奥运会游泳冠军汪顺和代表火炬线上传递参与者的“虚拟数字火炬手”一同点燃了杭州亚运会的主火炬台.某校社会实践小组为了测量这座主火炬台顶端距离地面的高度,如图,小明先在地面上处垂直于地面竖立了高度为米的标杆,这时地面上的点,标杆的顶端点,火炬台的顶端正好在同一直线上,测得米;小明再从点出发沿着方向前进米,到达点.在点处放置一平面镜,小刚站在处时,恰好在平面镜中看到火炬顶端的像,此时测得小刚的眼睛到地面的距离为米,米.已知点与火炬台的底端在同一直线上,,,.(平面镜大小忽略不计)
(1)求与的等量关系;
(2)请你根据以上数据,计算该火炬台的高度.
14.(23-24九年级上·江西九江·期中)如图是的正方形网格,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹).
(1)如图1,在边上找一点P,使得.
(2)如图2,在边上找一点Q,使得.
15.(23-24九年级上·江西吉安·期中)已知,如图所示的四边形ABCD为菱形,AC、BD交于O,AF⊥BC于F,交于点E.
(1)求证:
(2)求证:;
(3)过点E作,若,交于点G,若菱形ABCD的面积为,求的长.
16.(23-24九年级上·江西景德镇·期中)如图,在△ABC中,DE∥BC,=.
(1)如果AD=4,求BD的长度;
(2)如果S△ADE=2,求S四边形DBCE的值.
17.(23-24九年级上·江西九江·期中)如图1,在纸片中,,,,D,E分别是,边上的动点,且,连接,将沿翻折,点B落在点F的位置,连接.
(1)如图2,当点F在边上时,求的长.
(2)如图3,点在运动过程中,当时,求的长.
18.(23-24九年级上·江西景德镇·期中)如图1.已知四边形是矩形.点在的延长线上.与相交于点,与相交于点
求证:;
若,求的长;
如图2,连接,求证:.
19.(23-24九年级上·江西鹰潭·期中)如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
① 当时, ;② 当时,
(2)拓展探究
试判断:当0°≤α<360°时,的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.
20.(23-24九年级上·江西萍乡·期中)问题背景:一次数学综合实践活动课上,小慧发现并证明了关于三角形角平分线的一个结论.如图①,已知是的角平分线,可证.小慧的证明思路是:如图②,过点C作,交的延长线于点E,构造相似三角形来证明尝试证明:
(1)请参照小慧提供的思路,利用图②证明:.
应用拓展:
(2)如图③,在中,,D是边上一点,连接,将沿所在直线折叠,点C恰好落在边上的E点处.若,,求的长.
21.(23-24九年级上·江西吉安·期中)如图,在四边形ABCD中,G是DC上的点,连接BG,点F是BG上的点,在BC上取点H,使,连接HF,CF,AF.
(1)①如图1,点F为正方形ABCD中对角线AC上一点,求证:;
②如图2,在正方形ABCD中,若于F,求证:.
(2)如图3,若四边形ABCD为菱形,
①直接写出与之间的数量关系;
②若,.,,求AH的长;
22.(23-24九年级上·江西景德镇·期中)如图(1),已知点G在正方形ABCD的对角线AC上,GE⊥BC,垂足为点E,GF⊥CD,垂足为点F.
(1)证明与推断:
①求证:四边形CEGF是正方形;
②推断:的值为 :
(2)探究与证明:
将正方形CEGF绕点C顺时针方向旋转α角(0°<α<45°),如图(2)所示,试探究线段AG与BE之间的数量关系,并说明理由:
(3)拓展与运用:
正方形CEGF在旋转过程中,当B,E,F三点在一条直线上时,如图(3)所示,延长CG交AD于点H.若AG=6,GH=2,则BC= .
参考答案:
1.A
【详解】解:、任意两个等腰直角三角形,根据等腰直角三角形的性质,两腰分别相等,它们两边的比值成比例,夹角为直角相等,根据相似三角形的判定定理可得任意两个等腰直角三角形相似,故符合题意;
、任意两个直角三角形,根据三角形相似的判定定理不能得到任意两个直角三角形相似,故不符合题意;
、任意两个等腰三角形,根据三角形相似的判定定理不能得到任意两个等腰三角形相似,故不符合题意;
、任意两个锐角三角形,根据三角形相似的判定定理不能得到任意两个锐角三角形相似,故不符合题意;
故选:.
2.A
【详解】解:∵△ABC与△DEF位似,点O为位似中心.
∴△ABC∽△DEF,OB:OE= 1:2,
∴△ABC与△DEF的周长比是:1:2.
故选:A.
3.C
【详解】解:A、∵,
∴,故本选项不符合题意;
B、∵,
∴,故本选项不符合题意;
C、由图形可知,只有,不能判断,故本选项符合题意;
D、∵,
∴,故本选项不符合题意;
故选:C.
4.
【详解】解:∵,
∴,
故答案为:.
5./
【详解】解:∵点是线段的中点,
∴,
∵四边形与四边形是位似图形,
∴,
故答案为:.
6.
【详解】解:由相似多边形的性质可知,,
∴,解得,,
故答案为:.
7.
【详解】解:∵点C是线段的黄金分割点,且,
∴,
∴,
∵,
∴,
故答案为:.
8.1
【详解】解:∵C,D两点都是的黄金分割点,
∴,
,,
∴,
将,代入,
得:,
∴,
整理得:,
,
故答案为:1.
9.2或或12
【详解】解:与,,,
当与为对应边,
,
,,,
,
,
,
当与为对应边,
,
,,,
,
,
或12,
综上所述:当的值为2或或12时相似.
故答案为:2或8.4或12.
10.(1)证明见详解;
(2);
【详解】(1)证明:∵四边形是正方形,
∴,,
∵,,
∴,
∴;
(2)解:∵四边形是正方形,
∴,,
∴,
∴,
∴,
∵正方形的边长为4,,,
∴,,,
∴,
∴,
∴.
11.(1);
(2),理由见解析
【详解】(1)解:,
;
故答案为; ;
(2)解:.
证明:在的正方形方格中,
,,
.
,, ,
,.
∴
.
12.这双高跟鞋的高度偏高
【详解】解:设这双高跟鞋的高度为时,人体上半身长和下半身长成黄金比例,
由题意得:,
解得:,
,
这双高跟鞋的高度偏高.
13.(1),理由见解析;
(2)该火炬台的高度米.
【详解】(1)解:,理由:
∵点与火炬台的底端在同一直线上,,,
∴,
∴,
∴,
∵米,米,
∴,
∴;
(2)解:由题意得:米,
∴(米),
∵点与火炬台的底端在同一直线上,,,
∴,
∴,
∴,
∵米,米,
∴,即,
由()得:,
∴,
∴(米),
答:该火炬台的高度为米.
14.(1)见解析
(2)见解析
【详解】(1)如图所示,点P即为所求.
证明:由网格的特点可得,,,
∴
又∵
∴;
(2)如图所示,确定点M,然后连接连接交于点Q,点Q即为所求.
证明:由网格的特点可得,
是横4竖2的长方形的对角线,是横2竖4的长方形的对角线,
∴
∴
∴
∵
∴
又∵
∴;
15.(1)见解析
(2)见解析
(3)
【详解】(1)证明:∵对顶角相等
∴
∵菱形
∴且平分与(菱形两对角线互相垂直平分)
∵
∴
∵
∴
∴(两角对应相等的两三角形相似)
(2)由(1)得,
∴
∵菱形
∴,BD=2OD
∴即
∴,
∴(两角对应相等的两三角形相似)
∴
∴
∴.
(3)∵菱形面积为,
∴
∵D
∴
∴
设,则,BD=3m
由(2)得:
∴
在中,,
∴
此时
(舍去负值)
则
∵,
∴
∴
∴.
16.(1)BD=6;(2)S四边形DBCE=.
【详解】(1)∵DE∥BC,
∴△ADE∽△ABC,
∴=,
∵=,AD=4,
∴=,
∴BD=6;
(2)∵△ADE∽△ABC,=,
∴=()2,
∵S△ADE=2,
∴=()2,
解得:S四边形DBCE=.
17.(1)
(2)
【详解】(1)解:由翻折的性质可得: ,
∵
∴
∴四边形是菱形
∴
∴
∴
∴
在中,,,
∴
∴
设 ,则:
∵
∴
解得:
∴;
(2)解:如图,作,交于点;
∵
∴
∵四边形是菱形
∴ ,
∵
∴四边形是平行四边形
∴ ,
∴ ,
∴
在中
在中
.
18.(1)见解析;(2);(3)见解析
【详解】(1)∵四边形ABCD是矩形,
∴∠BAD=∠EAD=90 ,AO=BC,AD∥BC,
在△EAF和△DAB,
,
∴△EAF≌△DAB(SAS),
∴∠E=∠BDA,
∵∠BDA+∠ABD=90 ,
∴∠E+∠ABD=90 ,
∴∠EGB=90 ,
∴BG⊥EC;
(2)设AE=x,则EB=1+x,BC=AD=AE=x,
∵AF∥BC,∠E=∠E,
∴△EAF∽△EBC,
∴,又AF=AB=1,
∴即,
解得:,(舍去)
即AE=;
(3)在EG上截取EH=DG,连接AH,
在△EAH和△DAG,
,
∴△EAH≌△DAG(SAS),
∴∠EAH=∠DAG,AH=AG,
∵∠EAH+∠DAH=90 ,
∴∠DAG+∠DAH=90 ,
∴∠HAG=90 ,
∴△GAH是等腰直角三角形,
∴即,
∴GH=AG,
∵GH=EG-EH=EG-DG,
∴.
19.(1)①,②.(2)无变化;理由参见解析.(3),.
【详解】(1)①当α=0°时,
∵Rt△ABC中,∠B=90°,
∴AC=,
∵点D、E分别是边BC、AC的中点,
∴,BD=8÷2=4,
∴.
②如图1,
,
当α=180°时,
可得AB∥DE,
∵,
∴
(2)如图2,
,
当0°≤α<360°时,的大小没有变化,
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵,
∴△ECA∽△DCB,
∴.
(3)①如图3,
,
∵AC=4,CD=4,CD⊥AD,
∴AD=
∵AD=BC,AB=DC,∠B=90°,
∴四边形ABCD是矩形,
∴BD=AC=.
②如图4,连接BD,过点D作AC的垂线交AC于点Q,过点B作AC的垂线交AC于点P,
,
∵AC=,CD=4,CD⊥AD,
∴AD=,
∵点D、E分别是边BC、AC的中点,
∴DE==2,
∴AE=AD-DE=8-2=6,
由(2),可得
,
∴BD=.
综上所述,BD的长为或.
20.(1)见解析(2)
【详解】(1)证明:∵,
∴,,
∴,
∴,
∵,,
∴,
∴,
∴.
(2)∵将沿所在直线折叠,点C恰好落在边上的E点处,
∴,,
由(1)可知,,
又∵,
∴
∴,
∵,
∴
∴,
∴,
∴;
∴.
21.(1)①见解析;②见解析
(2)①+=180°;②
【详解】(1)①∵点F为正方形ABCD中对角线AC上一点,
∴AC平分,
∴∠GCF=∠HCF
又∵,
∴,
∴;
②∵由,,,
可得,
∴,,
∵,,
∴,
∴,
∴;
(2)①+=180°,
理由:∵∠CFB=∠BCD,∠FBC=∠FBC,
∴△BFC∽ △BCG,
∴,,
又∵CG=CH,AB=BC,
∴,
∵∠ABF=∠FCB,
∴△CFH ∽△BFA,
∴∠CHF=∠FAB,
∵∠CHF+∠BHF=180°,
∴+=180°;
②由,,
得,
∴,,
又∵,,
∴,
∴,得,
∵∠CHF+∠BHF=180°,
∴+=180°,
∵,
∴,与互补,
将AH绕着点H逆时针旋转120度至,可得,
连接,可得,
∴,,
∴点A、B、共线,
∵.
∴是以120°为顶点的等腰三角形,
易得,即,
∴.
22.(1)①四边形CEGF是正方形;②;(2)线段AG与BE之间的数量关系为AG=BE;(3)3
【详解】(1)①∵四边形ABCD是正方形,
∴∠BCD=90°,∠BCA=45°,
∵GE⊥BC、GF⊥CD,
∴∠CEG=∠CFG=∠ECF=90°,
∴四边形CEGF是矩形,∠CGE=∠ECG=45°,
∴EG=EC,
∴四边形CEGF是正方形;
②由①知四边形CEGF是正方形,
∴∠CEG=∠B=90°,∠ECG=45°,
∴,GE∥AB,
∴,
故答案为;
(2)连接CG,
由旋转性质知∠BCE=∠ACG=α,
在Rt△CEG和Rt△CBA中,
=、=,
∴=,
∴△ACG∽△BCE,
∴,
∴线段AG与BE之间的数量关系为AG=BE;
(3)∵∠CEF=45°,点B、E、F三点共线,
∴∠BEC=135°,
∵△ACG∽△BCE,
∴∠AGC=∠BEC=135°,
∴∠AGH=∠CAH=45°,
∵∠CHA=∠AHG,
∴△AHG∽△CHA,
∴,
设BC=CD=AD=a,则AC=a,
则由得,
∴AH=a,
则DH=AD﹣AH=a,CH==a,
∴由得,
解得:a=3,即BC=3,
故答案为3
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
