14.2 乘法公式 同步练习(含答案)2024—2025学年人教版数学八年级上册
文档属性
| 名称 | 14.2 乘法公式 同步练习(含答案)2024—2025学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 300.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 20:27:16 | ||
图片预览


文档简介
0
14.2 乘法公式 同步练习2024—2025学年人教版数学八年级上册
一、单选题
1.若代数式 ,则 ( )
A.-8 B.9 C.8 D.-9
2.如图,将长方形的各边向外作正方形,若四个正方形周长之和为24,面积之和为12,则长方形的面积为( )
A.4 B. C.5 D.6
3.下列等式成立的是( )
A. B.
C. D.
4.如图,有A,B,C三种卡片,其中A型卡片是边长为 的正方形,B型卡片是长为 ,宽为 的长方形( ),C型卡片是边长为 的正方形.如果要用它们拼成边长为( )的正方形,则需A、B、C三种卡片共( )张.
A.23 B.24 C.25 D.26
5.下列多项式乘法中,不能用平方差公式计算的是( )
A. B.
C. D.
6.下列计算正确的是( )
A.(a+b)2=a2+b2 B.(a+b)2=a2+ab+b2
C.(a-b)2=a2+2ab-b2 D.(a-b)2=a2-2ab+b2
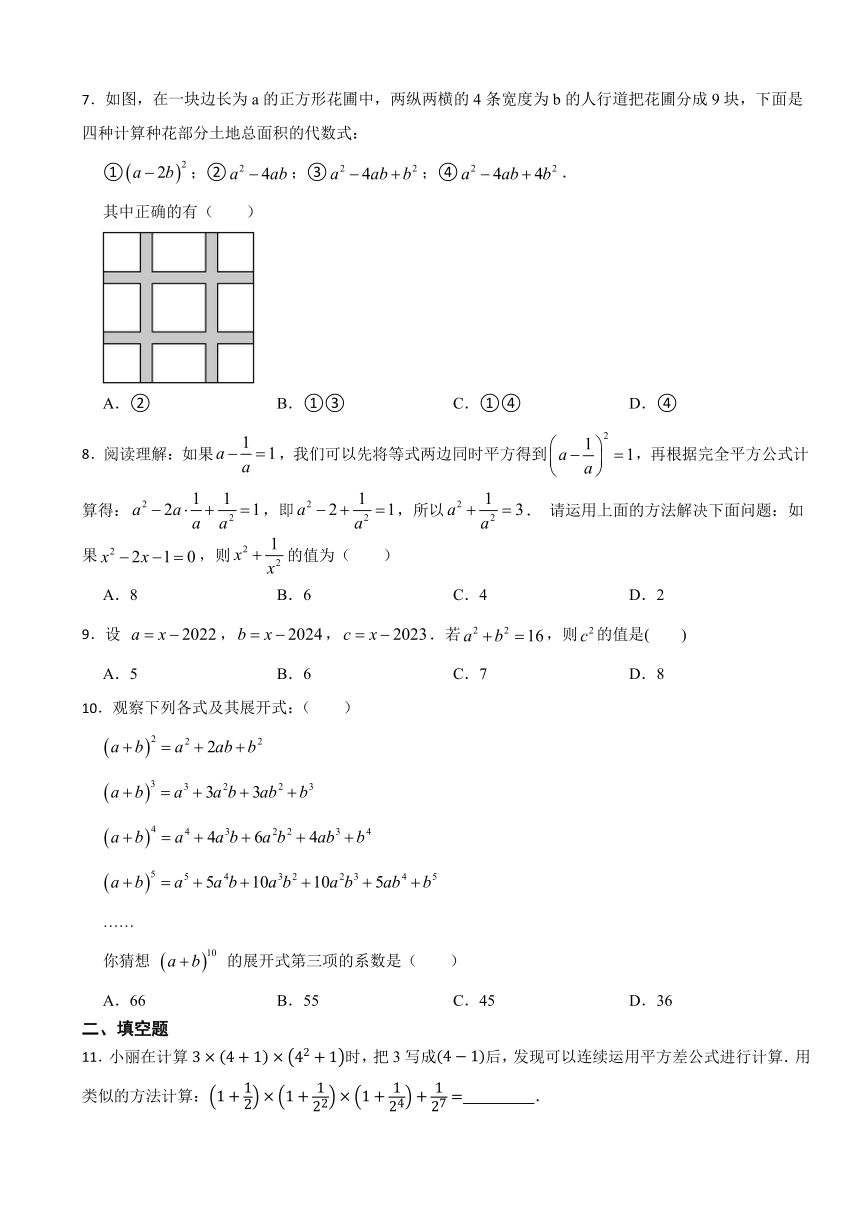
7.如图,在一块边长为a的正方形花圃中,两纵两横的4条宽度为b的人行道把花圃分成9块,下面是四种计算种花部分土地总面积的代数式:
①;②;③;④.
其中正确的有( )
A.② B.①③ C.①④ D.④
8.阅读理解:如果,我们可以先将等式两边同时平方得到,再根据完全平方公式计算得:,即,所以. 请运用上面的方法解决下面问题:如果,则的值为( )
A.8 B.6 C.4 D.2
9.设 ,,.若,则的值是( )
A.5 B.6 C.7 D.8
10.观察下列各式及其展开式:( )
……
你猜想 的展开式第三项的系数是( )
A.66 B.55 C.45 D.36
二、填空题
11.小丽在计算时,把3写成后,发现可以连续运用平方差公式进行计算.用类似的方法计算: .
12.一元二次方程化为一般形式为 .
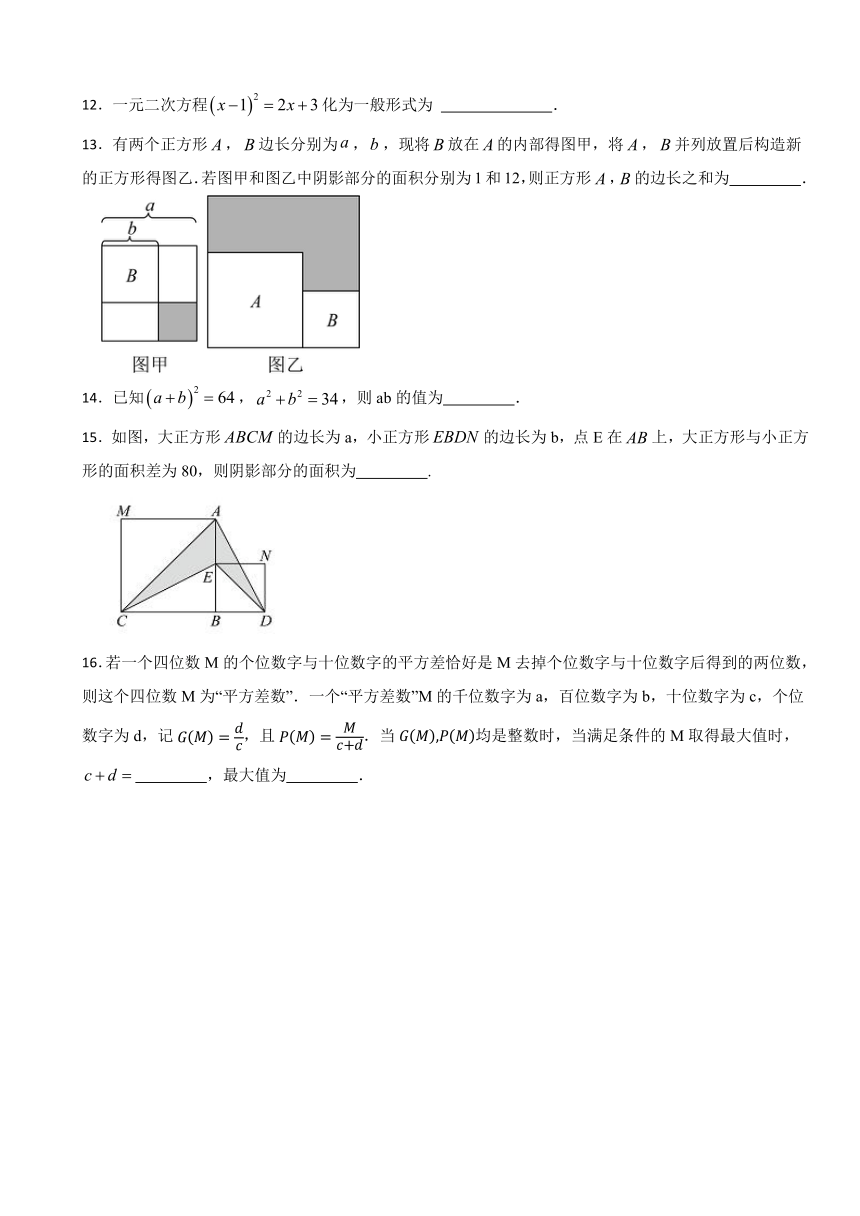
13.有两个正方形,边长分别为,,现将放在的内部得图甲,将,并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形,的边长之和为 .
14.已知,,则ab的值为 .
15.如图,大正方形的边长为a,小正方形的边长为b,点E在上,大正方形与小正方形的面积差为80,则阴影部分的面积为 .
16.若一个四位数M的个位数字与十位数字的平方差恰好是M去掉个位数字与十位数字后得到的两位数,则这个四位数M为“平方差数”.一个“平方差数”M的千位数字为a,百位数字为b,十位数字为c,个位数字为d,记,且.当均是整数时,当满足条件的M取得最大值时, ,最大值为 .
三、解答题
17.如图,对一个正方形进行了分割:
(1)请用两种不同的方法求图中大正方形的面积:
方法1:___________,方法2:___________.
(2)根据(1)中的结论,请你写出代数式,,之间的等量关系为__________;
(3)利用等量关系解决问题:,,求.
18.通过用两种不同的方法计算同一个图形的面积,可以得到一个代数恒等式.如图①是一个长为,宽为m的长方形,沿图中虚线用剪刀平均分成四个小长方形,然后按图②的方式拼成一个大正方形.
(1)请用两种不同的方法表示图②中阴影部分的面积(直接用含m,n的代数式表示):
方法一:___________________________________;
方法二:___________________________________;
(2)根据(1)中的结论,请你写出代数式之间的等量关系为___________________________________;
(3)根据(2)中的等量关系及课本所学的完全平方公式知识,解决如下问题:
①若实数a,b满足:,,求的值.
②若,求的值.
19.现有长与宽分别为a、b的小长方形若干个,用两个这样的小长方形,拼成如图1的图形,用四个相同的小长方形拼成图2的图形,请认真观察图形,解答下列问题:
(1)根据图中条件,请写出图1和图2所验证的关于a、b的关系式;(用a、b的代数式表示出来)
图1表示: ;
图2表示: ;
(2)根据上面的解题思路与方法,解决下列问题:
若,,求和的值;
(3)如图3,点C是线段上的一点,以,为边向两边作正方形,设,两正方形的面积和,则图中阴影部分面积是 .
20.数学活动课上,老师准备了若干个如图1的三种纸片(其中A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是边长分别为a、b的长方形),并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)观察图2,请你写出下列三个代数式:之间的等量关系:__________.
(2)若要拼出一个面积为的矩形,则需要A号卡片__________张,B号卡片__________张,C号卡片__________张;
(3)根据(1)中得出的等量关系,解决如下问题:已知,求的值;
(4)两个正方形,如图3摆放,边长分别为x,y.若,则图中阴影部分面积的和为__________.
21.数学课上,老师准备了三种纸片,如图1中边长分别为a、b的正方形纸片A、B,以及长为b、宽为a的长方形纸片C,观察图形并解答下列问题:
(1)小玲想用图1的三种纸片拼出一个面积为的大长方形,则需要A纸片 张,B纸片 张,C纸片 张(空格处填写数字)
(2)①观察图2,请写出下列三个代数式,,之间的等量关系:_______________.
②根据①中的关系,若x满足,则的值为 .
(3)已知正方形的边长为x,E,F分别是上的点,且,长方形的面积是8,分别以为边作正方形,求阴影部分的面积.
答案解析部分
1.C
2.B
3.D
4.C
5.B
6.D
7.C
8.B
9.C
10.C
11.2
12.
13.5
14.15
15.40
16.9;6318
17.(1),
(2)
(3)13
18.(1);
(2)
(3)①7;②
19.(1);
(2)解:∵,
∴,
∵,,
∴,
.
(3)5
20.(1)
(2);
(3);
(4).
21.(1)3,1,4
(2)①;②7
(3)12
14.2 乘法公式 同步练习2024—2025学年人教版数学八年级上册
一、单选题
1.若代数式 ,则 ( )
A.-8 B.9 C.8 D.-9
2.如图,将长方形的各边向外作正方形,若四个正方形周长之和为24,面积之和为12,则长方形的面积为( )
A.4 B. C.5 D.6
3.下列等式成立的是( )
A. B.
C. D.
4.如图,有A,B,C三种卡片,其中A型卡片是边长为 的正方形,B型卡片是长为 ,宽为 的长方形( ),C型卡片是边长为 的正方形.如果要用它们拼成边长为( )的正方形,则需A、B、C三种卡片共( )张.
A.23 B.24 C.25 D.26
5.下列多项式乘法中,不能用平方差公式计算的是( )
A. B.
C. D.
6.下列计算正确的是( )
A.(a+b)2=a2+b2 B.(a+b)2=a2+ab+b2
C.(a-b)2=a2+2ab-b2 D.(a-b)2=a2-2ab+b2
7.如图,在一块边长为a的正方形花圃中,两纵两横的4条宽度为b的人行道把花圃分成9块,下面是四种计算种花部分土地总面积的代数式:
①;②;③;④.
其中正确的有( )
A.② B.①③ C.①④ D.④
8.阅读理解:如果,我们可以先将等式两边同时平方得到,再根据完全平方公式计算得:,即,所以. 请运用上面的方法解决下面问题:如果,则的值为( )
A.8 B.6 C.4 D.2
9.设 ,,.若,则的值是( )
A.5 B.6 C.7 D.8
10.观察下列各式及其展开式:( )
……
你猜想 的展开式第三项的系数是( )
A.66 B.55 C.45 D.36
二、填空题
11.小丽在计算时,把3写成后,发现可以连续运用平方差公式进行计算.用类似的方法计算: .
12.一元二次方程化为一般形式为 .
13.有两个正方形,边长分别为,,现将放在的内部得图甲,将,并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形,的边长之和为 .
14.已知,,则ab的值为 .
15.如图,大正方形的边长为a,小正方形的边长为b,点E在上,大正方形与小正方形的面积差为80,则阴影部分的面积为 .
16.若一个四位数M的个位数字与十位数字的平方差恰好是M去掉个位数字与十位数字后得到的两位数,则这个四位数M为“平方差数”.一个“平方差数”M的千位数字为a,百位数字为b,十位数字为c,个位数字为d,记,且.当均是整数时,当满足条件的M取得最大值时, ,最大值为 .
三、解答题
17.如图,对一个正方形进行了分割:
(1)请用两种不同的方法求图中大正方形的面积:
方法1:___________,方法2:___________.
(2)根据(1)中的结论,请你写出代数式,,之间的等量关系为__________;
(3)利用等量关系解决问题:,,求.
18.通过用两种不同的方法计算同一个图形的面积,可以得到一个代数恒等式.如图①是一个长为,宽为m的长方形,沿图中虚线用剪刀平均分成四个小长方形,然后按图②的方式拼成一个大正方形.
(1)请用两种不同的方法表示图②中阴影部分的面积(直接用含m,n的代数式表示):
方法一:___________________________________;
方法二:___________________________________;
(2)根据(1)中的结论,请你写出代数式之间的等量关系为___________________________________;
(3)根据(2)中的等量关系及课本所学的完全平方公式知识,解决如下问题:
①若实数a,b满足:,,求的值.
②若,求的值.
19.现有长与宽分别为a、b的小长方形若干个,用两个这样的小长方形,拼成如图1的图形,用四个相同的小长方形拼成图2的图形,请认真观察图形,解答下列问题:
(1)根据图中条件,请写出图1和图2所验证的关于a、b的关系式;(用a、b的代数式表示出来)
图1表示: ;
图2表示: ;
(2)根据上面的解题思路与方法,解决下列问题:
若,,求和的值;
(3)如图3,点C是线段上的一点,以,为边向两边作正方形,设,两正方形的面积和,则图中阴影部分面积是 .
20.数学活动课上,老师准备了若干个如图1的三种纸片(其中A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是边长分别为a、b的长方形),并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)观察图2,请你写出下列三个代数式:之间的等量关系:__________.
(2)若要拼出一个面积为的矩形,则需要A号卡片__________张,B号卡片__________张,C号卡片__________张;
(3)根据(1)中得出的等量关系,解决如下问题:已知,求的值;
(4)两个正方形,如图3摆放,边长分别为x,y.若,则图中阴影部分面积的和为__________.
21.数学课上,老师准备了三种纸片,如图1中边长分别为a、b的正方形纸片A、B,以及长为b、宽为a的长方形纸片C,观察图形并解答下列问题:
(1)小玲想用图1的三种纸片拼出一个面积为的大长方形,则需要A纸片 张,B纸片 张,C纸片 张(空格处填写数字)
(2)①观察图2,请写出下列三个代数式,,之间的等量关系:_______________.
②根据①中的关系,若x满足,则的值为 .
(3)已知正方形的边长为x,E,F分别是上的点,且,长方形的面积是8,分别以为边作正方形,求阴影部分的面积.
答案解析部分
1.C
2.B
3.D
4.C
5.B
6.D
7.C
8.B
9.C
10.C
11.2
12.
13.5
14.15
15.40
16.9;6318
17.(1),
(2)
(3)13
18.(1);
(2)
(3)①7;②
19.(1);
(2)解:∵,
∴,
∵,,
∴,
.
(3)5
20.(1)
(2);
(3);
(4).
21.(1)3,1,4
(2)①;②7
(3)12
