2024-2025学年浙江省杭州市西湖区公益中学九年级(上)月考数学试卷(10月份)(含答案)
文档属性
| 名称 | 2024-2025学年浙江省杭州市西湖区公益中学九年级(上)月考数学试卷(10月份)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 167.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-03 15:32:28 | ||
图片预览



文档简介
2024-2025学年浙江省杭州市西湖区公益中学九年级(上)月考数学试卷(10月份)
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.将如图所示的图案以圆心为中心,旋转后得到的图案是( )
A. B. C. D.
2.下列说法正确的是( )
A. “明天会下雨”是必然事件
B. “概率为的事件”是不可能事件
C. 测试自行车的质量应采取全面普查
D. 任意掷一枚质地均匀的硬币次,正面向上的次数不一定是次
3.已知的半径为,点在内,则的长可能是( )
A. B. C. D.
4.将抛物线先向左平移个单位,再向下平移个单位,所得抛物线的表达式为( )
A. B.
C. D.
5.如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是( )
A. B. C. D.
6.小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
A. B. C. D. 均不可能
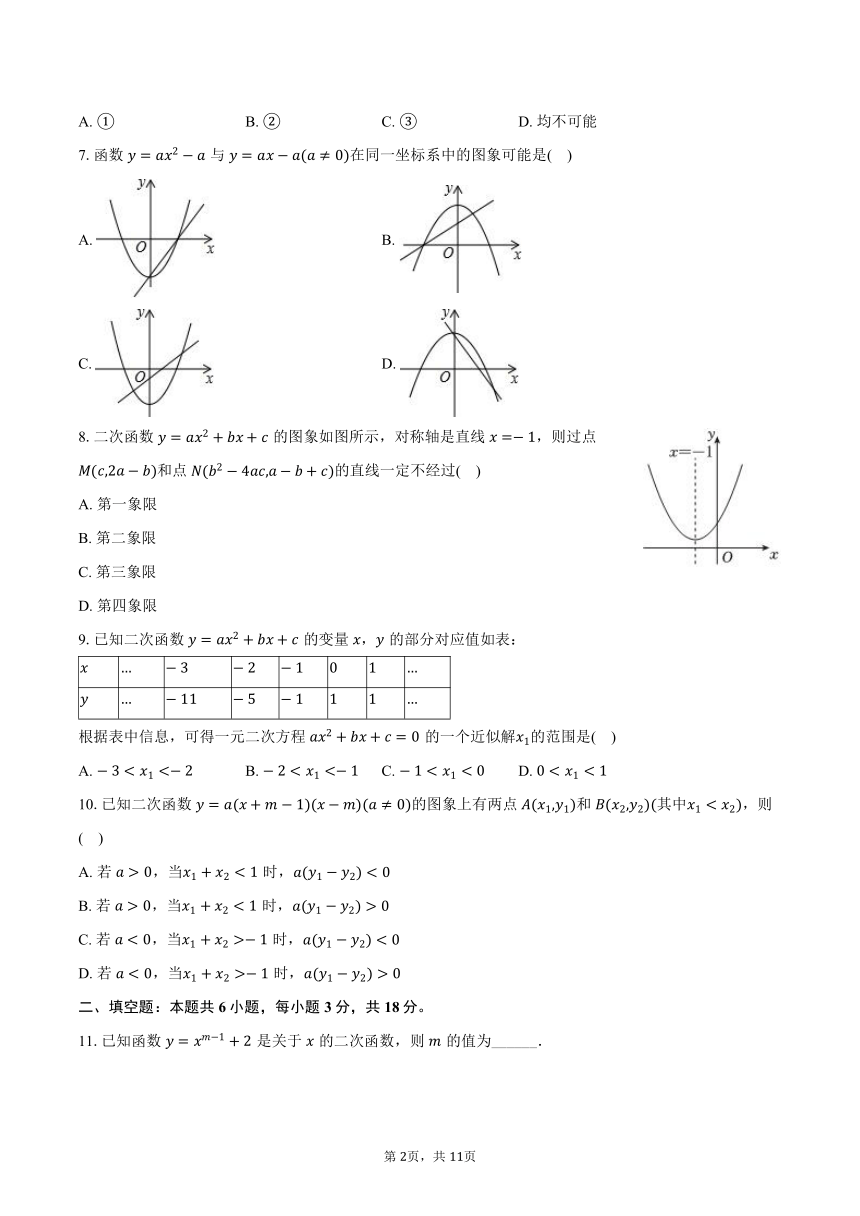
7.函数与在同一坐标系中的图象可能是( )
A. B.
C. D.
8.二次函数的图象如图所示,对称轴是直线,则过点和点的直线一定不经过( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
9.已知二次函数的变量,的部分对应值如表:
根据表中信息,可得一元二次方程的一个近似解的范围是( )
A. B. C. D.
10.已知二次函数的图象上有两点和其中,则( )
A. 若,当时,
B. 若,当时,
C. 若,当时,
D. 若,当时,
二、填空题:本题共6小题,每小题3分,共18分。
11.已知函数是关于的二次函数,则的值为______.
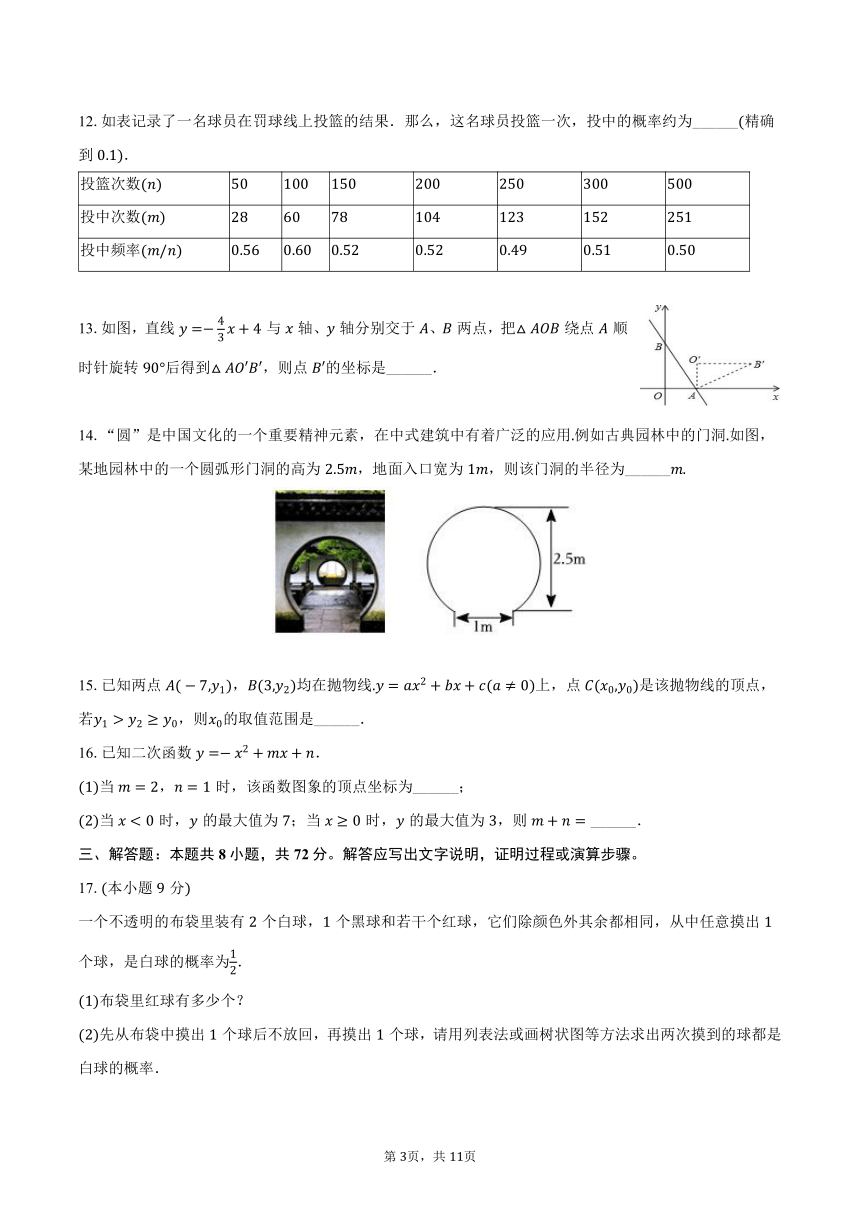
12.如表记录了一名球员在罚球线上投篮的结果.那么,这名球员投篮一次,投中的概率约为______精确到.
投篮次数
投中次数
投中频率
13.如图,直线与轴、轴分别交于、两点,把绕点顺时针旋转后得到,则点的坐标是______.
14.“圆”是中国文化的一个重要精神元素,在中式建筑中有着广泛的应用例如古典园林中的门洞如图,某地园林中的一个圆弧形门洞的高为,地面入口宽为,则该门洞的半径为______
15.已知两点,均在抛物线上,点是该抛物线的顶点,若,则的取值范围是______.
16.已知二次函数.
当,时,该函数图象的顶点坐标为______;
当时,的最大值为;当时,的最大值为,则 ______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
一个不透明的布袋里装有个白球,个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出个球,是白球的概率为.
布袋里红球有多少个?
先从布袋中摸出个球后不放回,再摸出个球,请用列表法或画树状图等方法求出两次摸到的球都是白球的概率.
18.本小题分
如图,已知抛物线经过、两点.
求抛物线的解析式和顶点坐标;
当时,求的取值范围.
19.本小题分
在的方格纸中,的三个顶点都在格点上.
以点为旋转中心,将按顺时针方向旋转,画出旋转后的;
在的基础上,求线段和线段夹角的度数.
20.本小题分
已知二次函数.
求函数图象与轴的公共点的个数;
若,在二次函数图象上,试比较与的大小.
21.本小题分
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角两边足够长,用长的篱笆围成一个矩形花园篱笆只围,两边,设.
若花园的面积为,求的值;
若在处有一棵树与墙,的距离分别是和,要将这棵树围在花园内含边界,不考虑树的粗细,求花园面积的最大值.
22.本小题分
如图为桥洞的形状,其正视图是由圆弧和矩形构成点为所在的圆心,点又恰好在为水面处若桥洞跨度为米,拱高弦于点为米.
求所在的半径;
若河里行驶来一艘正视图为矩形的船,其宽米,露出水面的高度为米,求船能通过桥洞时的最大高度.
23.本小题分
已知点在抛物线为常数,上.
若,,
求抛物线的解析式;
若点,在该二次函数的图象上,且点在对称轴左侧、点在对称轴右侧,若,求的取值范围;
若时,总有,且当时总有,求的值.
24.本小题分
在平面直角坐标系中,设二次函数,是实数,且
已知,若的对称轴为直线,求的对称轴;
若函数图象经过点,点,求证:函数的图象也经过、两点;
设函数和函数的最小值互为相反数求的值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:设红球的个数为,由题意可得:
,
解得:,经检验是方程的根,
即红球的个数为个;
画树状图如下:
摸得两白.
18.解:抛物线经过、两点,
,解得,
抛物线解析式为,
顶点坐标为;
,
抛物线开口向上,对称轴为直线,
当时,随的增大而减小,当时,随的增大而增大,
当时,当时,有最大值为,当时,有最小值为,
当时,当时,有最大值为,当时,有最小值为,
当时,.
19.解:如图,即为所求;
绕点顺时针旋转得到,
,,
,
,
,
,
,
线段和线段夹角的度数为.
20.解:,
,
,
函数图象与轴有个公共点;
二次函数的对称轴为直线,
,
,,
,
抛物线开口向上,当时,随的增大而增大,
.
21.解:,则,
,
解得:,,
答:的值为或;
,
,
,
在处有一棵树与墙,的距离分别是和,
,
,
当时,取到最大值为:,
答:花园面积的最大值为平方米.
22.解:弦于点,为米,为米,
垂直平分,,,
在中,,
则,
解得:;
答:所在的半径为;
如图所示:假设矩形的船为矩形,船沿中点为中心通过,
连接,
,,
在中,,
则,
解得:,
答:船能通过桥洞时的最大高度为.
23.解:将坐标代入,
得,
解得,
抛物线的解析式为.
抛物线的对称轴方程是,
根据题意,得,
解得.
当时,,与题意不符,
.
抛物线开口向下,对称轴方程为,
当时,随的增大而增大;当时,随的增大而减小,
当时,,
将坐标代入,
得,
解得.
24.解:抛物线与轴交点为,,对称轴为直线,
的对称轴为直线,
,
,
联立方程,
解得,
,
的对称轴为直线.
证明:,
把代入得,
把代入得,
,
把代入得,
把代入得,
函数的图象也经过、两点.
由题意得,
与轴交点坐标为,,
对称轴为直线,
把代入得最小值为,
同理将代入得最小值为,
,
整理得,
.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.将如图所示的图案以圆心为中心,旋转后得到的图案是( )
A. B. C. D.
2.下列说法正确的是( )
A. “明天会下雨”是必然事件
B. “概率为的事件”是不可能事件
C. 测试自行车的质量应采取全面普查
D. 任意掷一枚质地均匀的硬币次,正面向上的次数不一定是次
3.已知的半径为,点在内,则的长可能是( )
A. B. C. D.
4.将抛物线先向左平移个单位,再向下平移个单位,所得抛物线的表达式为( )
A. B.
C. D.
5.如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是( )
A. B. C. D.
6.小明不慎把家里的圆形镜子打碎了,其中三块碎片如图所示,三块碎片中最有可能配到与原来一样大小的圆形镜子的碎片是( )
A. B. C. D. 均不可能
7.函数与在同一坐标系中的图象可能是( )
A. B.
C. D.
8.二次函数的图象如图所示,对称轴是直线,则过点和点的直线一定不经过( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
9.已知二次函数的变量,的部分对应值如表:
根据表中信息,可得一元二次方程的一个近似解的范围是( )
A. B. C. D.
10.已知二次函数的图象上有两点和其中,则( )
A. 若,当时,
B. 若,当时,
C. 若,当时,
D. 若,当时,
二、填空题:本题共6小题,每小题3分,共18分。
11.已知函数是关于的二次函数,则的值为______.
12.如表记录了一名球员在罚球线上投篮的结果.那么,这名球员投篮一次,投中的概率约为______精确到.
投篮次数
投中次数
投中频率
13.如图,直线与轴、轴分别交于、两点,把绕点顺时针旋转后得到,则点的坐标是______.
14.“圆”是中国文化的一个重要精神元素,在中式建筑中有着广泛的应用例如古典园林中的门洞如图,某地园林中的一个圆弧形门洞的高为,地面入口宽为,则该门洞的半径为______
15.已知两点,均在抛物线上,点是该抛物线的顶点,若,则的取值范围是______.
16.已知二次函数.
当,时,该函数图象的顶点坐标为______;
当时,的最大值为;当时,的最大值为,则 ______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
一个不透明的布袋里装有个白球,个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出个球,是白球的概率为.
布袋里红球有多少个?
先从布袋中摸出个球后不放回,再摸出个球,请用列表法或画树状图等方法求出两次摸到的球都是白球的概率.
18.本小题分
如图,已知抛物线经过、两点.
求抛物线的解析式和顶点坐标;
当时,求的取值范围.
19.本小题分
在的方格纸中,的三个顶点都在格点上.
以点为旋转中心,将按顺时针方向旋转,画出旋转后的;
在的基础上,求线段和线段夹角的度数.
20.本小题分
已知二次函数.
求函数图象与轴的公共点的个数;
若,在二次函数图象上,试比较与的大小.
21.本小题分
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角两边足够长,用长的篱笆围成一个矩形花园篱笆只围,两边,设.
若花园的面积为,求的值;
若在处有一棵树与墙,的距离分别是和,要将这棵树围在花园内含边界,不考虑树的粗细,求花园面积的最大值.
22.本小题分
如图为桥洞的形状,其正视图是由圆弧和矩形构成点为所在的圆心,点又恰好在为水面处若桥洞跨度为米,拱高弦于点为米.
求所在的半径;
若河里行驶来一艘正视图为矩形的船,其宽米,露出水面的高度为米,求船能通过桥洞时的最大高度.
23.本小题分
已知点在抛物线为常数,上.
若,,
求抛物线的解析式;
若点,在该二次函数的图象上,且点在对称轴左侧、点在对称轴右侧,若,求的取值范围;
若时,总有,且当时总有,求的值.
24.本小题分
在平面直角坐标系中,设二次函数,是实数,且
已知,若的对称轴为直线,求的对称轴;
若函数图象经过点,点,求证:函数的图象也经过、两点;
设函数和函数的最小值互为相反数求的值.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:设红球的个数为,由题意可得:
,
解得:,经检验是方程的根,
即红球的个数为个;
画树状图如下:
摸得两白.
18.解:抛物线经过、两点,
,解得,
抛物线解析式为,
顶点坐标为;
,
抛物线开口向上,对称轴为直线,
当时,随的增大而减小,当时,随的增大而增大,
当时,当时,有最大值为,当时,有最小值为,
当时,当时,有最大值为,当时,有最小值为,
当时,.
19.解:如图,即为所求;
绕点顺时针旋转得到,
,,
,
,
,
,
,
线段和线段夹角的度数为.
20.解:,
,
,
函数图象与轴有个公共点;
二次函数的对称轴为直线,
,
,,
,
抛物线开口向上,当时,随的增大而增大,
.
21.解:,则,
,
解得:,,
答:的值为或;
,
,
,
在处有一棵树与墙,的距离分别是和,
,
,
当时,取到最大值为:,
答:花园面积的最大值为平方米.
22.解:弦于点,为米,为米,
垂直平分,,,
在中,,
则,
解得:;
答:所在的半径为;
如图所示:假设矩形的船为矩形,船沿中点为中心通过,
连接,
,,
在中,,
则,
解得:,
答:船能通过桥洞时的最大高度为.
23.解:将坐标代入,
得,
解得,
抛物线的解析式为.
抛物线的对称轴方程是,
根据题意,得,
解得.
当时,,与题意不符,
.
抛物线开口向下,对称轴方程为,
当时,随的增大而增大;当时,随的增大而减小,
当时,,
将坐标代入,
得,
解得.
24.解:抛物线与轴交点为,,对称轴为直线,
的对称轴为直线,
,
,
联立方程,
解得,
,
的对称轴为直线.
证明:,
把代入得,
把代入得,
,
把代入得,
把代入得,
函数的图象也经过、两点.
由题意得,
与轴交点坐标为,,
对称轴为直线,
把代入得最小值为,
同理将代入得最小值为,
,
整理得,
.
第1页,共1页
同课章节目录
