4.4 一次函数的应用同步练习(含答案)2024—2025学年北师大版八年级数学上册
文档属性
| 名称 | 4.4 一次函数的应用同步练习(含答案)2024—2025学年北师大版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 584.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-04 00:00:00 | ||
图片预览




文档简介
4.4 一次函数的应用 同步练习2024—2025学年北师大版八年级数学上册
一、单选题
1.一次函数的图象与y轴交点的坐标是( )
A. B. C. D.
2.如图,一次函数的图象与轴、轴分别相交于、两点,点是直线上的一点,且将分为面积相等的两部分,则点的坐标为( )
A. B. C. D.
3.小明从家出发,徒步到书店购买文具,购好文具后骑共享单车原路返回,设他从家出发后所用的时间为t(分),离家的路程为S(米).则S与t之间的关系大致可以用图象表示为( )
A. B.
C. D.
4.已知一次函数y=-3x+1的图象过点(x1,y1),则y1,y2,y3的大小关系是( ).
A. B. C. D.
5.下列描述一次函数的图象及性质错误的是( )
A.直线与x轴交点坐标是 B.y随x的增大而减小
C.直线经过第一、二、四象限 D.当时,
6.下列函数图象中,能反映等腰三角形顶角(度)与底角(度)之间函数关系的是( )
A. B.
C. D.
7.甲、乙两车从A城出发前往B城,其中甲先出发,如图是甲、乙行驶路程(km),(km)与时间x(h)变化的图像,下列说法不正确的是( )
A.乙车开始行驶时,甲车在乙车前处
B.乙车的平均速度是
C.在距离A城处,乙车追上甲车
D.乙车比甲车早到B城
8.如图,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为两车之间的距离为,图中的折线表示与之间的函数关系,下列说法中错误的是( )
A.甲乙两地相距
B.点表示此时两车相遇
C.慢车的速度为
D.折线表示慢车先加速后减速最后到达甲地
9.如图,欣欣妈妈在超市购买某种水果所付金额y(元)与购买x(千克)之间的关系如图所示,则“一次性购买6千克这种水果”比“分2次每次购买3千克这种水果”可节省( )元.
A.4 B.3 C.2 D.1
10.甲、乙两车从地出发,匀速驶往地.乙车出发1后,甲车才沿相同的路线开始行驶.甲车先到达地并停留30分钟后,又以原速按原路线返回,直至与乙车相遇.图中的折线段表示从开始到相遇止,两车之间的距离()与甲车行驶的时间()的函数关系的图象,则( )
A.甲车的速度是120/ B., 两地的距离是360
C.乙车出发4.5时甲车到达地 D.甲车出发4.5最终与乙车相遇
二、填空题
11.点,在一次函数的图象上,则 (填“”“”或“”)
12.漏刻是我国古代的一种计时工具,它是中国古代人民对变量之间关系的创造性应用.小明制作了一个简单的漏刻模型,并研究发现每分钟水位上升的高度相同,水位和时间之间存在如表所示的关系,其中有一个h的值记录错误,请排除后利用正确的数据确定当t为时,对应的水位h为 .
… 1 2 3 5 …
… 4 …
13.在弹性限度内,某弹簧挂上重物后的总长度L(cm)与所挂物体质量x(kg)之间满足一次函数关系,且点均在其图像上,则L与x之间的函数关系式是 .(不必写出x的取值范围)
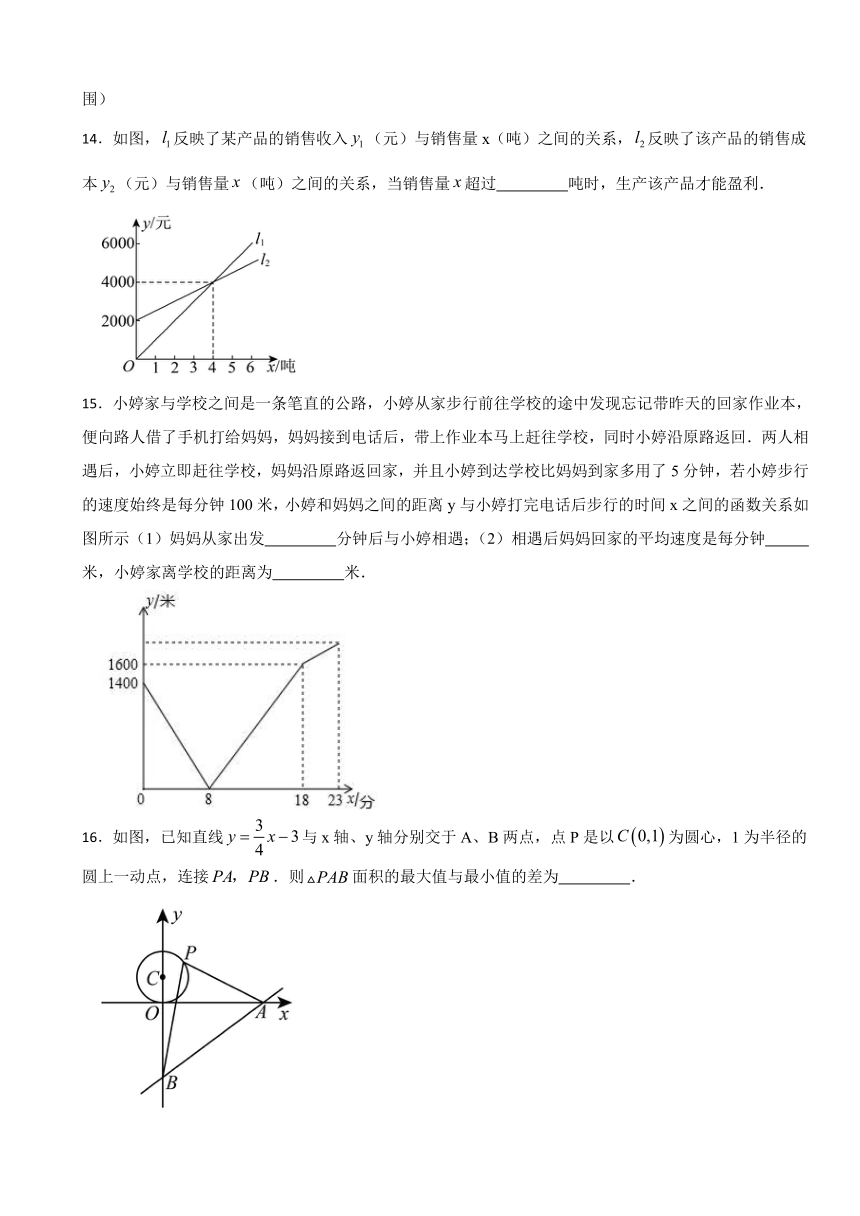
14.如图,反映了某产品的销售收入(元)与销售量x(吨)之间的关系,反映了该产品的销售成本(元)与销售量(吨)之间的关系,当销售量超过 吨时,生产该产品才能盈利.
15.小婷家与学校之间是一条笔直的公路,小婷从家步行前往学校的途中发现忘记带昨天的回家作业本,便向路人借了手机打给妈妈,妈妈接到电话后,带上作业本马上赶往学校,同时小婷沿原路返回.两人相遇后,小婷立即赶往学校,妈妈沿原路返回家,并且小婷到达学校比妈妈到家多用了5分钟,若小婷步行的速度始终是每分钟100米,小婷和妈妈之间的距离y与小婷打完电话后步行的时间x之间的函数关系如图所示(1)妈妈从家出发 分钟后与小婷相遇;(2)相遇后妈妈回家的平均速度是每分钟 米,小婷家离学校的距离为 米.
16.如图,已知直线与x轴、y轴分别交于A、B两点,点P是以为圆心,1为半径的圆上一动点,连接.则面积的最大值与最小值的差为 .
三、解答题
17.、两地之间有一条笔直的公路,甲、乙两车同时从地出发,匀速去往终点地,一段时间后甲车先到达终点,再过一段时间后,乙车也到达终点.两车行驶的路程之和与乙车行驶的时间之间的关系如图所示.
(1)、两地相距______;
(2)求的值;
(3)求甲车到达地后与之间的函数解析式.
18.小明用的练习本可以到甲超市购买,也可以到乙超市购买.已知两超市的标价都是每本1元,但甲超市的优惠条件是购买10本以上,从第11本开始按标价的70%卖.乙超市的优惠条件是从第1本开始就按标价的85%卖.
(1)当小明要买20本时,到哪家超市购买较省钱?
(2)写出甲超市中,收款(元)与购买本数x(本)(x>10)的关系式.
(3)小明现有24元钱,最多可买多少本练习本?
19.甲、乙两个工程组同时挖掘沈白高铁某段隧道,两组每天挖掘长度均保持不变,合作一段时间后,乙组因维修设备而停工,甲组单独完成了剩下的任务,甲、乙两组挖掘的长度之和y(m)与甲组挖掘时间x(天)之间的关系如图所示.
(1)甲组比乙组多挖掘了 天.
(2)求乙组停工后y关于x的函数解析式,并写出自变量x的取值范围.
(3)当甲组挖掘的总长度与乙组挖掘的总长度相等时,直接写出乙组已停工的天数.
20.疫情期间,某乳品公司计划向马关县红十字会捐赠一批牛奶,甲运输公司提出:每千克运费0.48元,不收取其他费用:乙运输公司提出:每千克运费0.28元,另收取其他费用600元.
(1)设这批牛奶共x千克,选择甲公司运输,所需费用为元,选择乙公司运输,所需费用为元,请分别写出,与x之间的关系式;
(2)该公司选择哪家运输公司运送这批牛奶更划算,请说明理由.
21.如图 ①,已知一条笔直的公路上有 三地, 地位于 两地之间. 甲车从 地出发, 驶向 地, 同时乙车从 地出发驶向 地, 到达 地并停留了 后, 按原路返回 地. 两车沿公路向速行驶, 甲车的速度比乙车的速度慢 , 设两车行驶时间为 . 图 ②中线段 和折线 分别表示甲、乙两车各自到 地的距离 与行驶的时间 的函数图象,请结合图象信息, 解答问题: 出发多少小时后, 行驶中的两车之间距离等于 ?
22.小聪和小明沿同一条笔直的马路同时从学校出发到某图书馆查阅资料,学校与图书馆的路程是5千米,小聪骑共享单车,小明步行.当小聪从原路回到学校时,小明刚好到达图书馆.图中折线和线段分别表示两人离学校的路程(千米)与所经过的时间(分钟)之间的函数关系,请根据图象回答下列问题:
(1)小聪在图书馆查阅资料的时间为_________分钟,小聪返回学校的速度为_________千米/分钟.
(2)求小聪从图书馆返回学校时离学校的路程(千米)与(分钟)之间的函数表达式,并写出自变量的取值范围.
(3)若设两人在路上相距不超过千米时称为“可控距离”,则小聪和小明“可控距离”的时间共有______分钟.
答案解析部分
1.B
2.C
3.A
4.B
5.A
6.B
7.D
8.D
9.C
10.C
11.
12.
13.
14.4
15.8;60;2100
16.5
17.(1)160
(2)4
(3)
18.(1)一样
(2)
(3)30本
19.(1)30
(2)解:设乙组停工后y关于x的函数解析式为:y=kx+b,点(30,210)(60,300)在图象上,
, 解得
∴函数关系式为:y=3x+120(30≤x≤60)
(3)解:10天
20.(1),
(2)当x>3000时选择乙公司,当021.解:由图像可知,甲的行驶速度为千米/时,
∴OD间的函数关系式为,
∴乙的行驶速度为千米/时,
地到地的距离千米,
,,
乙的速度不变,
,
设,
将代入得,
,
解得:,
乙车从地返回地时,GH间函数关系式为;
乙的速度为75千米/时,段经过,
,
,
解得:,
两车经过时相遇,
①当时,乙从向地行驶,
,
解得:,
②当时,乙在点,甲在距离点60千米处,
此时距离差为千米,
③当时,,
解得:,
④当时,由于乙的速度大于甲的速度,
乙距离甲越来越近,
,
解得:,
综上,出发时或时或时,两车相距20千米.
22.(1)15;0.5
(2)
(3)10
一、单选题
1.一次函数的图象与y轴交点的坐标是( )
A. B. C. D.
2.如图,一次函数的图象与轴、轴分别相交于、两点,点是直线上的一点,且将分为面积相等的两部分,则点的坐标为( )
A. B. C. D.
3.小明从家出发,徒步到书店购买文具,购好文具后骑共享单车原路返回,设他从家出发后所用的时间为t(分),离家的路程为S(米).则S与t之间的关系大致可以用图象表示为( )
A. B.
C. D.
4.已知一次函数y=-3x+1的图象过点(x1,y1),则y1,y2,y3的大小关系是( ).
A. B. C. D.
5.下列描述一次函数的图象及性质错误的是( )
A.直线与x轴交点坐标是 B.y随x的增大而减小
C.直线经过第一、二、四象限 D.当时,
6.下列函数图象中,能反映等腰三角形顶角(度)与底角(度)之间函数关系的是( )
A. B.
C. D.
7.甲、乙两车从A城出发前往B城,其中甲先出发,如图是甲、乙行驶路程(km),(km)与时间x(h)变化的图像,下列说法不正确的是( )
A.乙车开始行驶时,甲车在乙车前处
B.乙车的平均速度是
C.在距离A城处,乙车追上甲车
D.乙车比甲车早到B城
8.如图,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为两车之间的距离为,图中的折线表示与之间的函数关系,下列说法中错误的是( )
A.甲乙两地相距
B.点表示此时两车相遇
C.慢车的速度为
D.折线表示慢车先加速后减速最后到达甲地
9.如图,欣欣妈妈在超市购买某种水果所付金额y(元)与购买x(千克)之间的关系如图所示,则“一次性购买6千克这种水果”比“分2次每次购买3千克这种水果”可节省( )元.
A.4 B.3 C.2 D.1
10.甲、乙两车从地出发,匀速驶往地.乙车出发1后,甲车才沿相同的路线开始行驶.甲车先到达地并停留30分钟后,又以原速按原路线返回,直至与乙车相遇.图中的折线段表示从开始到相遇止,两车之间的距离()与甲车行驶的时间()的函数关系的图象,则( )
A.甲车的速度是120/ B., 两地的距离是360
C.乙车出发4.5时甲车到达地 D.甲车出发4.5最终与乙车相遇
二、填空题
11.点,在一次函数的图象上,则 (填“”“”或“”)
12.漏刻是我国古代的一种计时工具,它是中国古代人民对变量之间关系的创造性应用.小明制作了一个简单的漏刻模型,并研究发现每分钟水位上升的高度相同,水位和时间之间存在如表所示的关系,其中有一个h的值记录错误,请排除后利用正确的数据确定当t为时,对应的水位h为 .
… 1 2 3 5 …
… 4 …
13.在弹性限度内,某弹簧挂上重物后的总长度L(cm)与所挂物体质量x(kg)之间满足一次函数关系,且点均在其图像上,则L与x之间的函数关系式是 .(不必写出x的取值范围)
14.如图,反映了某产品的销售收入(元)与销售量x(吨)之间的关系,反映了该产品的销售成本(元)与销售量(吨)之间的关系,当销售量超过 吨时,生产该产品才能盈利.
15.小婷家与学校之间是一条笔直的公路,小婷从家步行前往学校的途中发现忘记带昨天的回家作业本,便向路人借了手机打给妈妈,妈妈接到电话后,带上作业本马上赶往学校,同时小婷沿原路返回.两人相遇后,小婷立即赶往学校,妈妈沿原路返回家,并且小婷到达学校比妈妈到家多用了5分钟,若小婷步行的速度始终是每分钟100米,小婷和妈妈之间的距离y与小婷打完电话后步行的时间x之间的函数关系如图所示(1)妈妈从家出发 分钟后与小婷相遇;(2)相遇后妈妈回家的平均速度是每分钟 米,小婷家离学校的距离为 米.
16.如图,已知直线与x轴、y轴分别交于A、B两点,点P是以为圆心,1为半径的圆上一动点,连接.则面积的最大值与最小值的差为 .
三、解答题
17.、两地之间有一条笔直的公路,甲、乙两车同时从地出发,匀速去往终点地,一段时间后甲车先到达终点,再过一段时间后,乙车也到达终点.两车行驶的路程之和与乙车行驶的时间之间的关系如图所示.
(1)、两地相距______;
(2)求的值;
(3)求甲车到达地后与之间的函数解析式.
18.小明用的练习本可以到甲超市购买,也可以到乙超市购买.已知两超市的标价都是每本1元,但甲超市的优惠条件是购买10本以上,从第11本开始按标价的70%卖.乙超市的优惠条件是从第1本开始就按标价的85%卖.
(1)当小明要买20本时,到哪家超市购买较省钱?
(2)写出甲超市中,收款(元)与购买本数x(本)(x>10)的关系式.
(3)小明现有24元钱,最多可买多少本练习本?
19.甲、乙两个工程组同时挖掘沈白高铁某段隧道,两组每天挖掘长度均保持不变,合作一段时间后,乙组因维修设备而停工,甲组单独完成了剩下的任务,甲、乙两组挖掘的长度之和y(m)与甲组挖掘时间x(天)之间的关系如图所示.
(1)甲组比乙组多挖掘了 天.
(2)求乙组停工后y关于x的函数解析式,并写出自变量x的取值范围.
(3)当甲组挖掘的总长度与乙组挖掘的总长度相等时,直接写出乙组已停工的天数.
20.疫情期间,某乳品公司计划向马关县红十字会捐赠一批牛奶,甲运输公司提出:每千克运费0.48元,不收取其他费用:乙运输公司提出:每千克运费0.28元,另收取其他费用600元.
(1)设这批牛奶共x千克,选择甲公司运输,所需费用为元,选择乙公司运输,所需费用为元,请分别写出,与x之间的关系式;
(2)该公司选择哪家运输公司运送这批牛奶更划算,请说明理由.
21.如图 ①,已知一条笔直的公路上有 三地, 地位于 两地之间. 甲车从 地出发, 驶向 地, 同时乙车从 地出发驶向 地, 到达 地并停留了 后, 按原路返回 地. 两车沿公路向速行驶, 甲车的速度比乙车的速度慢 , 设两车行驶时间为 . 图 ②中线段 和折线 分别表示甲、乙两车各自到 地的距离 与行驶的时间 的函数图象,请结合图象信息, 解答问题: 出发多少小时后, 行驶中的两车之间距离等于 ?
22.小聪和小明沿同一条笔直的马路同时从学校出发到某图书馆查阅资料,学校与图书馆的路程是5千米,小聪骑共享单车,小明步行.当小聪从原路回到学校时,小明刚好到达图书馆.图中折线和线段分别表示两人离学校的路程(千米)与所经过的时间(分钟)之间的函数关系,请根据图象回答下列问题:
(1)小聪在图书馆查阅资料的时间为_________分钟,小聪返回学校的速度为_________千米/分钟.
(2)求小聪从图书馆返回学校时离学校的路程(千米)与(分钟)之间的函数表达式,并写出自变量的取值范围.
(3)若设两人在路上相距不超过千米时称为“可控距离”,则小聪和小明“可控距离”的时间共有______分钟.
答案解析部分
1.B
2.C
3.A
4.B
5.A
6.B
7.D
8.D
9.C
10.C
11.
12.
13.
14.4
15.8;60;2100
16.5
17.(1)160
(2)4
(3)
18.(1)一样
(2)
(3)30本
19.(1)30
(2)解:设乙组停工后y关于x的函数解析式为:y=kx+b,点(30,210)(60,300)在图象上,
, 解得
∴函数关系式为:y=3x+120(30≤x≤60)
(3)解:10天
20.(1),
(2)当x>3000时选择乙公司,当0
∴OD间的函数关系式为,
∴乙的行驶速度为千米/时,
地到地的距离千米,
,,
乙的速度不变,
,
设,
将代入得,
,
解得:,
乙车从地返回地时,GH间函数关系式为;
乙的速度为75千米/时,段经过,
,
,
解得:,
两车经过时相遇,
①当时,乙从向地行驶,
,
解得:,
②当时,乙在点,甲在距离点60千米处,
此时距离差为千米,
③当时,,
解得:,
④当时,由于乙的速度大于甲的速度,
乙距离甲越来越近,
,
解得:,
综上,出发时或时或时,两车相距20千米.
22.(1)15;0.5
(2)
(3)10
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
