2025人教版高中物理必修第二册强化练习题--第六章 圆周运动拔高练(有解析)
文档属性
| 名称 | 2025人教版高中物理必修第二册强化练习题--第六章 圆周运动拔高练(有解析) |  | |
| 格式 | docx | ||
| 文件大小 | 584.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-05 23:55:33 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教版高中物理必修第二册
综合拔高练
五年高考练
考点1 描述圆周运动的物理量
1.(2024黑吉辽,2)“指尖转球”是花式篮球表演中常见的技巧。如图,当篮球在指尖上绕轴转动时,球面上P、Q两点做圆周运动的 ( )
半径相等
B.线速度大小相等
向心加速度大小相等
D.角速度大小相等
2.(2023全国甲,17)一质点做匀速圆周运动,若其所受合力的大小与轨道半径的n次方成正比,运动周期与轨道半径成反比,则n等于 ( )
A.1 B.2 C.3 D.4
考点2 圆周运动的分析与计算
3.(2024江苏,11)如图所示,细绳穿过竖直的管子拴住一个小球,让小球在A高度处做水平面内的匀速圆周运动,现用力将细绳缓慢下拉,使小球在B高度处水平面内做匀速圆周运动,不计一切摩擦,则 ( )
A.周期TAC.线速度vA>vB D.向心加速度aA>aB
4.(2024广东,5)如图所示,在细绳的拉动下,半径为r的卷轴可绕其固定的中心点O在水平面内转动。卷轴上沿半径方向固定着长度为l的细管,管底在O点。细管内有一根原长为、劲度系数为k的轻质弹簧,弹簧底端固定在管底,顶端连接质量为m、可视为质点的插销。当以速度v匀速拉动细绳时,插销做匀速圆周运动。若v过大,插销会卡进固定的端盖。使卷轴转动停止。忽略摩擦力,弹簧在弹性限度内。要使卷轴转动不停止,v的最大值为 ( )
A.r B.l C.r D.l
5.(2024江西,14)雪地转椅是一种游乐项目,其中心传动装置带动转椅在雪地上滑动。如图(a)、(b)所示,传动装置有一高度可调的水平圆盘,可绕通过中心O点的竖直轴匀速转动。圆盘边缘A处固定连接一轻绳,轻绳另一端B连接转椅(视为质点)。转椅运动稳定后,其角速度与圆盘角速度相等。转椅与雪地之间的动摩擦因数为μ,重力加速度为g,不计空气阻力。
(1)在图(a)中,若圆盘在水平雪地上以角速度ω1匀速转动,转椅运动稳定后在水平雪地上绕O点做半径为r1的匀速圆周运动。求AB与OB之间夹角α的正切值。
(2)将圆盘升高,如图(b)所示。圆盘匀速转动,转椅运动稳定后在水平雪地上绕O1点做半径为r2的匀速圆周运动,绳子与竖直方向的夹角为θ,绳子在水平雪地上的投影A1B与O1B的夹角为β。求此时圆盘的角速度ω2。
6.(2023福建,15)一种离心测速器的简化工作原理如图所示。细杆的一端固定在竖直转轴OO'上的O点,并可随轴一起转动。杆上套有一轻质弹簧,弹簧一端固定于O点,另一端与套在杆上的圆环相连。当测速器稳定工作时,圆环将相对细杆静止,通过圆环的位置可以确定细杆匀速转动的角速度。已知细杆长度l=0.2 m,杆与竖直转轴的夹角α始终为60°,弹簧原长x0=0.1 m,弹簧劲度系数k=100 N/m,圆环质量m=1 kg;弹簧始终在弹性限度内,重力加速度大小取10 m/s2,摩擦力可忽略不计。
(1)若细杆和圆环处于静止状态,求圆环到O点的距离;
(2)求弹簧处于原长时,细杆匀速转动的角速度大小;
(3)求圆环处于细杆末端P时,细杆匀速转动的角速度大小。
考点3 圆周运动与直线运动、平抛运动的综合
7.(2022山东,8)无人配送小车某次性能测试路径如图所示,半径为3 m的半圆弧BC与长8 m的直线路径AB相切于B点,与半径为4 m的半圆弧CD相切于C点。小车以最大速度从A点驶入路径,到适当位置调整速率运动到B点,然后保持速率不变依次经过BC和CD。为保证安全,小车速率最大为4 m/s,在ABC段的加速度最大为2 m/s2,CD段的加速度最大为1 m/s2。小车视为质点,小车从A到D所需最短时间t及在AB段做匀速直线运动的最长距离l为 ( )
A.t= s,l=8 m
B.t= s,l=5 m
C.t= s,l=5.5 m
D.t= s,l=5.5 m
8.(多选题)(2022河北,10)如图,广场水平地面上同种盆栽紧密排列在以O为圆心、R1和R2为半径的同心圆上,圆心处装有竖直细水管,其上端水平喷水嘴的高度、出水速度及转动的角速度均可调节,以保障喷出的水全部落入相应的花盆中。依次给内圈和外圈上的盆栽浇水时,喷水嘴的高度、出水速度及转动的角速度分别用h1、v1、ω1和h2、v2、ω2表示。花盆大小相同,半径远小于同心圆半径,出水口截面积保持不变,忽略喷水嘴水平长度和空气阻力。下列说法正确的是 ( )
A.若h1=h2,则v1∶v2=R2∶R1
B.若v1=v2,则h1∶h2=∶
C.若ω1=ω2,v1=v2,喷水嘴各转动一周,则落入每个花盆的水量相同
D.若h1=h2,喷水嘴各转动一周且落入每个花盆的水量相同,则ω1=ω2
三年模拟练
应用实践
1.(2024河南南阳六校期末)2024年江原道冬青奥运会短道速滑女子1 500米决赛中,中国选手杨婧茹和李金恣利用“兔子战术”包揽冠亚军。图1是其比赛过程中的一段U形赛道,图2为其示意图,图中有①②两条路径,其中路径①的半圆部分半径为r,路径②的半径为2r。比赛开始时,李金恣沿路径①跟队滑行,杨婧茹沿路径②超越对手。若两人与冰面间的动摩擦因数均为μ,从M到M'和从N到N'的过程中均以转弯时不侧滑的最大速率运动,下列选项正确的是 ( )
A.李、杨两人在圆弧部分的向心加速度大小不同
B.李、杨两人通过的路程之比为
C.李、杨两人的速率之比为
D.李、杨两人所用时间之比为
2.(2024重庆渝中巴蜀中学月考)如图所示,半径为r的圆筒绕竖直中心轴OO'匀速转动,质量为m的小物块A靠在圆筒的内壁上,质量为m的小物块B和质量为的小物块C分别放在筒底距中心轴、处,三个小物块均与圆筒保持相对静止。若三个小物块与圆筒接触面间的动摩擦因数均为μ,最大静摩擦力等于滑动摩擦力,则μ的最小值为 ( )
A. B. C. D.
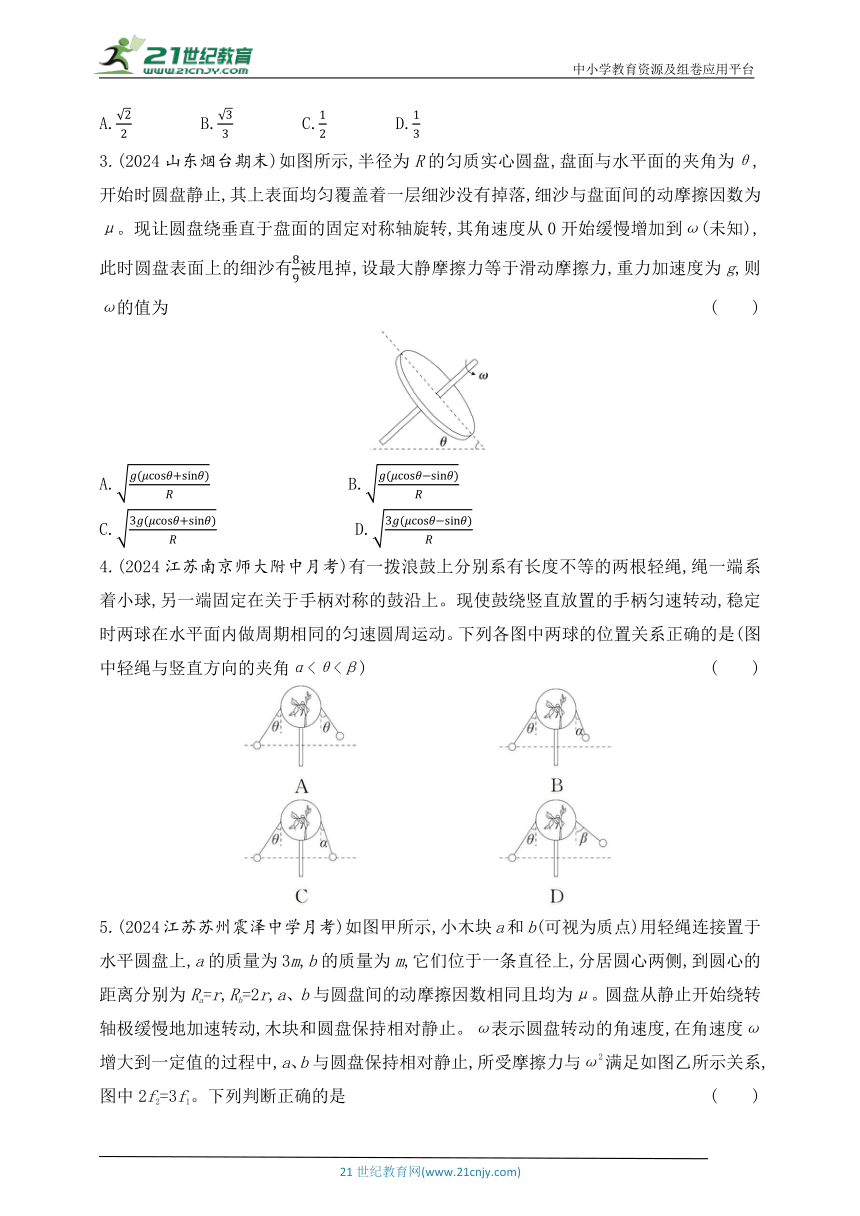
3.(2024山东烟台期末)如图所示,半径为R的匀质实心圆盘,盘面与水平面的夹角为θ,开始时圆盘静止,其上表面均匀覆盖着一层细沙没有掉落,细沙与盘面间的动摩擦因数为μ。现让圆盘绕垂直于盘面的固定对称轴旋转,其角速度从0开始缓慢增加到ω(未知),此时圆盘表面上的细沙有被甩掉,设最大静摩擦力等于滑动摩擦力,重力加速度为g,则ω的值为 ( )
A. B.
C. D.
4.(2024江苏南京师大附中月考)有一拨浪鼓上分别系有长度不等的两根轻绳,绳一端系着小球,另一端固定在关于手柄对称的鼓沿上。现使鼓绕竖直放置的手柄匀速转动,稳定时两球在水平面内做周期相同的匀速圆周运动。下列各图中两球的位置关系正确的是(图中轻绳与竖直方向的夹角α<θ<β) ( )
5.(2024江苏苏州震泽中学月考)如图甲所示,小木块a和b(可视为质点)用轻绳连接置于水平圆盘上,a的质量为3m,b的质量为m,它们位于一条直径上,分居圆心两侧,到圆心的距离分别为Ra=r,Rb=2r,a、b与圆盘间的动摩擦因数相同且均为μ。圆盘从静止开始绕转轴极缓慢地加速转动,木块和圆盘保持相对静止。ω表示圆盘转动的角速度,在角速度ω增大到一定值的过程中,a、b与圆盘保持相对静止,所受摩擦力与ω2满足如图乙所示关系,图中2f2=3f1。下列判断正确的是 ( )
A.图线(1)对应a B.ω3=ω2
C.ω2=ω1 D.ω=ω3时绳上张力为6f1
6.(2024江苏南京期中)图甲为某型号蛙式打夯机的实物图。打夯机工作过程中周期性地将夯头(连同支架)抬高到一定高度然后落下,把地面夯实。其结构可以简化为图乙。质量为m的铁球通过轻杆与转轮1相连,转轮1与底座的总质量为M,转轮1与转轮2之间通过轻质皮带连接,两轮半径之比为1∶2。转轮2在电动机作用下转动,通过轻质皮带使转轮1一起转动,转轮1带着铁球绕轴做圆周运动,球的转动半径为L,重力加速度为g。
(1)当转轮2以角速度ω匀速转动时,求铁球转动的线速度大小v1;
(2)若铁球转动到最高点时底座恰好对地面无压力,求此时铁球的线速度大小v2;
(3)当铁球以(2)中的线速度大小匀速转动,求底座对地面的最大压力的大小。
迁移创新
7.(2023广东汕头金山中学期中)如图所示为某弹射游戏装置示意图,通过拉杆将弹射器的轻质弹簧压缩后释放,将质量为0.1 kg的小滑块从A点水平弹出,滑行一段距离后经过B点,无碰撞地进入圆弧式细口径管道BCD,最后从D点水平飞出,并抛入在平台上的收集框EFGH中。小滑块与框底部碰撞后水平方向分速度不变,竖直方向分速度大小不变,方向竖直向上。整个轨道处在同一竖直面内,其中CD部分为半径R=0.4 m的圆弧管道,其圆心为O1。管口D点距平台的高度h=0.45 m,以D点正下方平台上的O点为原点向右建x轴。已知HE=EF=GF=d=0.25 m。管的口径远远小于圆弧半径,不计空气阻力、滑块的大小和框的厚度,重力加速度g取10 m/s2。
(1)若收集框的E点坐标xE=0.2 m,小滑块恰好擦着H点进入框中,求小滑块从D点飞出时对轨道的作用力;
(2)若小滑块直接击中收集框的底部反弹一次后,未出框且恰好击中收集框上的G点,则小球从D点飞出的速度大小v与收集框的E点坐标xE之间应满足什么关系
答案与分层梯度式解析
综合拔高练
五年高考练
1.D 由图可看出Q点做圆周运动的半径大于P点做圆周运动的半径,A错误;两点同轴转动,角速度大小相等,D正确;由v=ωr知线速度大小不相等,B错误;由a=ω2r知向心加速度大小不相等,C错误。
2.C 由题意可知,合力的表达式为F合=k1rn,周期T=,用周期表示向心力,为F向=mr=mr3,由F合=F向可得n=3,C正确。
3.B
模型建构 如图,摆长为l,摆线与竖直方向的夹角为θ,对摆球受力分析,由牛顿第二定律得mg tan θ=mr,r=l sin θ,解得T=2π=2π。
解析 小球由A高度处到B高度处运动,高度h变小,由T=2π=2π,可知TA>TB,A错误;因ω=,TA>TB,所以ωA<ωB,B正确;对小球分析有mg tan θ=m,整理得v=sin θ,由于绳子长度l变小,角θ变大,所以线速度大小变化无法判断,C错误;由于小球的向心加速度a=g tan θ,角度θ变大,所以向心加速度大小变大,即aA4.A 由题意可知当插销刚卡进固定端盖时弹簧的伸长量为Δx=,根据胡克定律有F=kΔx=,插销与卷轴同轴转动,角速度相同,对插销,由弹力提供向心力,有F=mlω2,对卷轴有v=rω,联立解得v=r,选项A正确。
5.答案 (1) (2)
解析 (1)在水平方向,对转椅受力分析如图1所示,所受拉力和摩擦力的合力提供向心力,根据平行四边形定则及牛顿第二定律可知==mr1
解得:tan α=
(2)转椅所受拉力与摩擦力如图2所示,将拉力沿竖直方向和BA1方向分解,竖直方向受力平衡,有
F'T cos θ+F'N=mg
F'T沿BA1方向的分力与Ff'的合力提供向心力(如图3),有==mr2
由图3可知,F'T sin θ sin β=μF'N
联立可得:ω2=
6.答案 (1)0.05 m (2) rad/s (3)10 rad/s
解析 (1)细杆和圆环处于平衡状态,对圆环由平衡条件得弹簧弹力T0=mg cos α=5 N
根据胡克定律F=kΔx得Δx0==0.05 m
弹簧弹力方向沿杆向上,故弹簧处于压缩状态,弹簧此时的长度即圆环到O点的距离x1=x0-Δx0=0.05 m。
(2)若弹簧处于原长,则圆环仅受重力和支持力,其合力使圆环在水平面内做匀速圆周运动。根据牛顿第二定律得=mr,由几何关系得圆环此时转动的半径r=x0 sin α,
联立并代入数据解得ω0= rad/s。
(3)圆环处于细杆末端P时,弹簧伸长量Δx'=l-x0,根据胡克定律得弹簧弹力T=k(l-x0)=10 N
圆环竖直方向受力平衡,有mg+T cos α=N sin α
水平方向合力提供向心力,则有
T sin α+N cos α=mω2r'
由几何关系得r'=l sin α
联立并代入数据解得ω=10 rad/s。
考情分析 圆周运动是曲线运动中的重要模型,试题往往创设生活实践情境,与圆周运动相结合,综合考查匀速圆周运动知识、牛顿第二定律、匀变速运动规律等,几乎每年高考都有涉及。
7.B 根据a=可知,在BC段、CD段的最大速率分别为vBC== m/s、vCD==2 m/s,在BC段、CD段的速率不变,因此在两圆弧段运动的最大速率v=2 m/s,通过两圆弧的时间为t2=+= s,小车从A点以最大速率v0=4 m/s匀速经过一段距离l之后开始减速,恰好到B点时速率为2 m/s,根据匀变速直线运动规律得v2-=-2a1(8 m-l),解得l=5 m,在AB段经历时间t1=+= s,因此总时间为t= s,选项B正确。
8.BD 根据平抛运动规律有h=gt2、R=v0t,若h1=h2,则喷出去的水在空中运动时间相等,所以=,选项A错误;根据平抛运动规律,得=,若v1=v2,化简得=,选项B正确;浇水时水的流量Q=Sv0,其中S是出水口横截面积,浇水一周总水量为V总=Q·=S·v0,若ω1=ω2,v1=v2,则总水量相同,但半径越大,摆放的花盆越多,所以落入每个花盆的水量越小,选项C错误;设每个花盆的直径大小为d,则半径为R的圆上能摆放的盆数为n=,浇水一周总水量V总=Q·=SR,落入每个花盆的水量V0==,若h1=h2,落入每个花盆的水量相同,则ω1=ω2,选项D正确。
教材溯源 本题以盆栽浇水为情境,来源于教材第20页第2题图5-7,在此基础上水管做圆周运动,创设平抛运动与圆周运动相结合的物理模型,综合考查匀速圆周运动的角速度、周期、平抛运动规律等知识。
三年模拟练
1.D 李、杨两人在水平U形赛道运动时,与冰面间的动摩擦因数均为μ,且均以转弯时不侧滑的最大速率运动,则最大静摩擦力提供向心力,有μm1g=m1a=m1,μm2g=m2a=m2,可知两人在圆弧部分的向心加速度大小相等,均为a1=a2=μg,李、杨两人的速率之比为==,故A、C错误;李、杨两人通过的路程之比为==,则所用时间之比为==·=·=,B错误,D正确。
2.A 对筒底的小物块,有f=mRω2,N=mg,当静摩擦力取最大值时,有f=μN,联立解得临界角速度ω=,可知转速增大时,B将先滑动,小物块B将要滑动时的角速度ω=;对小物块A受力分析,有N'=mrω2,f'=mg(点拨:竖直方向静摩擦力等于重力),当静摩擦力等于最大静摩擦力时,有f'=μN',联立解得μ=,所以μ=,A正确。
3.D 根据Fn=mω2r可知,在角速度相同的情况下,半径越大,所需的向心力越大,所以圆盘上最外层的细沙随着角速度的增大最先发生滑动(破题关键)。因为圆盘表面上的细沙有被甩掉,即面积上的细沙发生滑动,剩下未滑动,设未滑动部分的半径为r,则πr2=πR2,解得r=R,在最低点有mg(μ cos θ-sin θ)=mω2r(点拨:细沙在最低点最易发生滑动),解得ω=,D正确。
4.B 设绳长为L,绳子与竖直方向的夹角为δ,则由合力提供向心力得mg tan δ=m(L sin δ+r),化简得=L cos δ+,可知L越大,δ越大;设小球到绳上端的竖直距离为h,则由合力提供向心力得mg tan δ=m(h tan δ+r),化简得=h+,可知δ越大,h越大,选B。
5.D 角速度较小时,a、b两木块所受的静摩擦力提供向心力,对a有fa=3mrω2,对b有fb=2mrω2,则角速度较小时,b的静摩擦力较小,则图线(1)对应木块b,A错误;当角速度达到ω1时,b受的最大静摩擦力提供向心力,有f1=μmg=2mr,角速度继续增大,轻绳上出现弹力,当角速度达到ω2时,a达到最大静摩擦力,设此时轻绳的拉力大小为T,对a、b有T+3μmg=3mr,T+μmg=2mr,解得ω2=2ω1,故C错误;角速度继续增大,绳上拉力增大,a的静摩擦力不变,b所受的静摩擦力减小,当角速度达到ω3时,b所受的静摩擦力为零,设此时绳子拉力大小为T',对a、b有T'+3μmg=3mr,T'=2mr,解得ω3=ω2,故B错误;由上述分析可知ω3=ω2,ω2=2ω1,f1=μmg=2mr,T'=2mr,联立解得T'=6f1,故D正确。
6.答案 (1)2ωL (2) (3)2(m+M)g
解析 (1)转轮1、2通过皮带传动,轮缘各点的线速度大小相等,根据v=ωr
可得,ω与r成反比,所以ω1=2ω
铁球与转轮1同轴转动,角速度相等,可得v1=2ωL
(2)底座对地面无压力,可知杆对底座的弹力竖直向上,且F=Mg
由牛顿第三定律可知,杆对铁球向下的弹力FN=F=Mg
对铁球有FN+mg=m
解得v2=
(3)当铁球运动到最低点时,底座对地面压力最大,对铁球,由牛顿第二定律可得T-mg=
解得T=(2m+M)g
根据牛顿第三定律可知,轻杆对底座的作用力大小为(2m+M)g,方向向下。
对底座,由平衡条件可知,地面对底座的支持力大小为2(m+M)g,所以底座对地面的最大压力为Fm=2(m+M)g
7.答案 (1)0.75 N,方向竖直向下
(2)v=(xE≤0.25 m)
解析 (1)根据平抛运动规律,水平方向有xE=vDt0
竖直方向有h-d=g
解得vD=1 m/s
在D点,设轨道对滑块的作用力方向竖直向下,由牛顿第二定律可得FN+mg=
解得滑块从D点飞出时FN=-0.75 N
即轨道对滑块的力大小为0.75 N,方向竖直向上。
根据牛顿第三定律,滑块对轨道的力大小为0.75 N,方向竖直向下。
(2)设小滑块击中收集框底部的点距离左边框为x,根据平抛运动规律,竖直方向有h=gt2
解得t=0.3 s
水平方向有xE+x=vt
落地时的竖直速度大小为vy=gt=3 m/s
反弹后恰好击中G点,竖直方向有d=vyt'-gt'2
解得向上运动的时间t'=0.1 s(另一根舍去)
水平方向有d-x=vt'
综上可解得v=
要使小滑块进入收集框,临界条件为恰好过H点,竖直方向有h-d=g
水平方向有xE=vt0
又因v=
综上解得xE=0.25 m
故小球从D点飞出的速度大小v与收集框的E点坐标xE之间应满足v=(xE≤0.25 m)
模型分析 本题涉及三个物理模型——平抛运动模型、轻杆模型和斜抛运动模型。
(1)滑块从D点飞出落入收集框EFGH过程做平抛运动,可画出滑块恰好过H的临界轨迹,利用平抛运动的相关规律求解问题;
(2)滑块在圆弧管道的CD部分运动时可类比轻杆模型,利用圆周运动规律求解相关问题;
(3)滑块击中收集框的底部反弹至收集框上的G点过程做斜上抛运动,运用运动的分解知识求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教版高中物理必修第二册
综合拔高练
五年高考练
考点1 描述圆周运动的物理量
1.(2024黑吉辽,2)“指尖转球”是花式篮球表演中常见的技巧。如图,当篮球在指尖上绕轴转动时,球面上P、Q两点做圆周运动的 ( )
半径相等
B.线速度大小相等
向心加速度大小相等
D.角速度大小相等
2.(2023全国甲,17)一质点做匀速圆周运动,若其所受合力的大小与轨道半径的n次方成正比,运动周期与轨道半径成反比,则n等于 ( )
A.1 B.2 C.3 D.4
考点2 圆周运动的分析与计算
3.(2024江苏,11)如图所示,细绳穿过竖直的管子拴住一个小球,让小球在A高度处做水平面内的匀速圆周运动,现用力将细绳缓慢下拉,使小球在B高度处水平面内做匀速圆周运动,不计一切摩擦,则 ( )
A.周期TA
4.(2024广东,5)如图所示,在细绳的拉动下,半径为r的卷轴可绕其固定的中心点O在水平面内转动。卷轴上沿半径方向固定着长度为l的细管,管底在O点。细管内有一根原长为、劲度系数为k的轻质弹簧,弹簧底端固定在管底,顶端连接质量为m、可视为质点的插销。当以速度v匀速拉动细绳时,插销做匀速圆周运动。若v过大,插销会卡进固定的端盖。使卷轴转动停止。忽略摩擦力,弹簧在弹性限度内。要使卷轴转动不停止,v的最大值为 ( )
A.r B.l C.r D.l
5.(2024江西,14)雪地转椅是一种游乐项目,其中心传动装置带动转椅在雪地上滑动。如图(a)、(b)所示,传动装置有一高度可调的水平圆盘,可绕通过中心O点的竖直轴匀速转动。圆盘边缘A处固定连接一轻绳,轻绳另一端B连接转椅(视为质点)。转椅运动稳定后,其角速度与圆盘角速度相等。转椅与雪地之间的动摩擦因数为μ,重力加速度为g,不计空气阻力。
(1)在图(a)中,若圆盘在水平雪地上以角速度ω1匀速转动,转椅运动稳定后在水平雪地上绕O点做半径为r1的匀速圆周运动。求AB与OB之间夹角α的正切值。
(2)将圆盘升高,如图(b)所示。圆盘匀速转动,转椅运动稳定后在水平雪地上绕O1点做半径为r2的匀速圆周运动,绳子与竖直方向的夹角为θ,绳子在水平雪地上的投影A1B与O1B的夹角为β。求此时圆盘的角速度ω2。
6.(2023福建,15)一种离心测速器的简化工作原理如图所示。细杆的一端固定在竖直转轴OO'上的O点,并可随轴一起转动。杆上套有一轻质弹簧,弹簧一端固定于O点,另一端与套在杆上的圆环相连。当测速器稳定工作时,圆环将相对细杆静止,通过圆环的位置可以确定细杆匀速转动的角速度。已知细杆长度l=0.2 m,杆与竖直转轴的夹角α始终为60°,弹簧原长x0=0.1 m,弹簧劲度系数k=100 N/m,圆环质量m=1 kg;弹簧始终在弹性限度内,重力加速度大小取10 m/s2,摩擦力可忽略不计。
(1)若细杆和圆环处于静止状态,求圆环到O点的距离;
(2)求弹簧处于原长时,细杆匀速转动的角速度大小;
(3)求圆环处于细杆末端P时,细杆匀速转动的角速度大小。
考点3 圆周运动与直线运动、平抛运动的综合
7.(2022山东,8)无人配送小车某次性能测试路径如图所示,半径为3 m的半圆弧BC与长8 m的直线路径AB相切于B点,与半径为4 m的半圆弧CD相切于C点。小车以最大速度从A点驶入路径,到适当位置调整速率运动到B点,然后保持速率不变依次经过BC和CD。为保证安全,小车速率最大为4 m/s,在ABC段的加速度最大为2 m/s2,CD段的加速度最大为1 m/s2。小车视为质点,小车从A到D所需最短时间t及在AB段做匀速直线运动的最长距离l为 ( )
A.t= s,l=8 m
B.t= s,l=5 m
C.t= s,l=5.5 m
D.t= s,l=5.5 m
8.(多选题)(2022河北,10)如图,广场水平地面上同种盆栽紧密排列在以O为圆心、R1和R2为半径的同心圆上,圆心处装有竖直细水管,其上端水平喷水嘴的高度、出水速度及转动的角速度均可调节,以保障喷出的水全部落入相应的花盆中。依次给内圈和外圈上的盆栽浇水时,喷水嘴的高度、出水速度及转动的角速度分别用h1、v1、ω1和h2、v2、ω2表示。花盆大小相同,半径远小于同心圆半径,出水口截面积保持不变,忽略喷水嘴水平长度和空气阻力。下列说法正确的是 ( )
A.若h1=h2,则v1∶v2=R2∶R1
B.若v1=v2,则h1∶h2=∶
C.若ω1=ω2,v1=v2,喷水嘴各转动一周,则落入每个花盆的水量相同
D.若h1=h2,喷水嘴各转动一周且落入每个花盆的水量相同,则ω1=ω2
三年模拟练
应用实践
1.(2024河南南阳六校期末)2024年江原道冬青奥运会短道速滑女子1 500米决赛中,中国选手杨婧茹和李金恣利用“兔子战术”包揽冠亚军。图1是其比赛过程中的一段U形赛道,图2为其示意图,图中有①②两条路径,其中路径①的半圆部分半径为r,路径②的半径为2r。比赛开始时,李金恣沿路径①跟队滑行,杨婧茹沿路径②超越对手。若两人与冰面间的动摩擦因数均为μ,从M到M'和从N到N'的过程中均以转弯时不侧滑的最大速率运动,下列选项正确的是 ( )
A.李、杨两人在圆弧部分的向心加速度大小不同
B.李、杨两人通过的路程之比为
C.李、杨两人的速率之比为
D.李、杨两人所用时间之比为
2.(2024重庆渝中巴蜀中学月考)如图所示,半径为r的圆筒绕竖直中心轴OO'匀速转动,质量为m的小物块A靠在圆筒的内壁上,质量为m的小物块B和质量为的小物块C分别放在筒底距中心轴、处,三个小物块均与圆筒保持相对静止。若三个小物块与圆筒接触面间的动摩擦因数均为μ,最大静摩擦力等于滑动摩擦力,则μ的最小值为 ( )
A. B. C. D.
3.(2024山东烟台期末)如图所示,半径为R的匀质实心圆盘,盘面与水平面的夹角为θ,开始时圆盘静止,其上表面均匀覆盖着一层细沙没有掉落,细沙与盘面间的动摩擦因数为μ。现让圆盘绕垂直于盘面的固定对称轴旋转,其角速度从0开始缓慢增加到ω(未知),此时圆盘表面上的细沙有被甩掉,设最大静摩擦力等于滑动摩擦力,重力加速度为g,则ω的值为 ( )
A. B.
C. D.
4.(2024江苏南京师大附中月考)有一拨浪鼓上分别系有长度不等的两根轻绳,绳一端系着小球,另一端固定在关于手柄对称的鼓沿上。现使鼓绕竖直放置的手柄匀速转动,稳定时两球在水平面内做周期相同的匀速圆周运动。下列各图中两球的位置关系正确的是(图中轻绳与竖直方向的夹角α<θ<β) ( )
5.(2024江苏苏州震泽中学月考)如图甲所示,小木块a和b(可视为质点)用轻绳连接置于水平圆盘上,a的质量为3m,b的质量为m,它们位于一条直径上,分居圆心两侧,到圆心的距离分别为Ra=r,Rb=2r,a、b与圆盘间的动摩擦因数相同且均为μ。圆盘从静止开始绕转轴极缓慢地加速转动,木块和圆盘保持相对静止。ω表示圆盘转动的角速度,在角速度ω增大到一定值的过程中,a、b与圆盘保持相对静止,所受摩擦力与ω2满足如图乙所示关系,图中2f2=3f1。下列判断正确的是 ( )
A.图线(1)对应a B.ω3=ω2
C.ω2=ω1 D.ω=ω3时绳上张力为6f1
6.(2024江苏南京期中)图甲为某型号蛙式打夯机的实物图。打夯机工作过程中周期性地将夯头(连同支架)抬高到一定高度然后落下,把地面夯实。其结构可以简化为图乙。质量为m的铁球通过轻杆与转轮1相连,转轮1与底座的总质量为M,转轮1与转轮2之间通过轻质皮带连接,两轮半径之比为1∶2。转轮2在电动机作用下转动,通过轻质皮带使转轮1一起转动,转轮1带着铁球绕轴做圆周运动,球的转动半径为L,重力加速度为g。
(1)当转轮2以角速度ω匀速转动时,求铁球转动的线速度大小v1;
(2)若铁球转动到最高点时底座恰好对地面无压力,求此时铁球的线速度大小v2;
(3)当铁球以(2)中的线速度大小匀速转动,求底座对地面的最大压力的大小。
迁移创新
7.(2023广东汕头金山中学期中)如图所示为某弹射游戏装置示意图,通过拉杆将弹射器的轻质弹簧压缩后释放,将质量为0.1 kg的小滑块从A点水平弹出,滑行一段距离后经过B点,无碰撞地进入圆弧式细口径管道BCD,最后从D点水平飞出,并抛入在平台上的收集框EFGH中。小滑块与框底部碰撞后水平方向分速度不变,竖直方向分速度大小不变,方向竖直向上。整个轨道处在同一竖直面内,其中CD部分为半径R=0.4 m的圆弧管道,其圆心为O1。管口D点距平台的高度h=0.45 m,以D点正下方平台上的O点为原点向右建x轴。已知HE=EF=GF=d=0.25 m。管的口径远远小于圆弧半径,不计空气阻力、滑块的大小和框的厚度,重力加速度g取10 m/s2。
(1)若收集框的E点坐标xE=0.2 m,小滑块恰好擦着H点进入框中,求小滑块从D点飞出时对轨道的作用力;
(2)若小滑块直接击中收集框的底部反弹一次后,未出框且恰好击中收集框上的G点,则小球从D点飞出的速度大小v与收集框的E点坐标xE之间应满足什么关系
答案与分层梯度式解析
综合拔高练
五年高考练
1.D 由图可看出Q点做圆周运动的半径大于P点做圆周运动的半径,A错误;两点同轴转动,角速度大小相等,D正确;由v=ωr知线速度大小不相等,B错误;由a=ω2r知向心加速度大小不相等,C错误。
2.C 由题意可知,合力的表达式为F合=k1rn,周期T=,用周期表示向心力,为F向=mr=mr3,由F合=F向可得n=3,C正确。
3.B
模型建构 如图,摆长为l,摆线与竖直方向的夹角为θ,对摆球受力分析,由牛顿第二定律得mg tan θ=mr,r=l sin θ,解得T=2π=2π。
解析 小球由A高度处到B高度处运动,高度h变小,由T=2π=2π,可知TA>TB,A错误;因ω=,TA>TB,所以ωA<ωB,B正确;对小球分析有mg tan θ=m,整理得v=sin θ,由于绳子长度l变小,角θ变大,所以线速度大小变化无法判断,C错误;由于小球的向心加速度a=g tan θ,角度θ变大,所以向心加速度大小变大,即aA
5.答案 (1) (2)
解析 (1)在水平方向,对转椅受力分析如图1所示,所受拉力和摩擦力的合力提供向心力,根据平行四边形定则及牛顿第二定律可知==mr1
解得:tan α=
(2)转椅所受拉力与摩擦力如图2所示,将拉力沿竖直方向和BA1方向分解,竖直方向受力平衡,有
F'T cos θ+F'N=mg
F'T沿BA1方向的分力与Ff'的合力提供向心力(如图3),有==mr2
由图3可知,F'T sin θ sin β=μF'N
联立可得:ω2=
6.答案 (1)0.05 m (2) rad/s (3)10 rad/s
解析 (1)细杆和圆环处于平衡状态,对圆环由平衡条件得弹簧弹力T0=mg cos α=5 N
根据胡克定律F=kΔx得Δx0==0.05 m
弹簧弹力方向沿杆向上,故弹簧处于压缩状态,弹簧此时的长度即圆环到O点的距离x1=x0-Δx0=0.05 m。
(2)若弹簧处于原长,则圆环仅受重力和支持力,其合力使圆环在水平面内做匀速圆周运动。根据牛顿第二定律得=mr,由几何关系得圆环此时转动的半径r=x0 sin α,
联立并代入数据解得ω0= rad/s。
(3)圆环处于细杆末端P时,弹簧伸长量Δx'=l-x0,根据胡克定律得弹簧弹力T=k(l-x0)=10 N
圆环竖直方向受力平衡,有mg+T cos α=N sin α
水平方向合力提供向心力,则有
T sin α+N cos α=mω2r'
由几何关系得r'=l sin α
联立并代入数据解得ω=10 rad/s。
考情分析 圆周运动是曲线运动中的重要模型,试题往往创设生活实践情境,与圆周运动相结合,综合考查匀速圆周运动知识、牛顿第二定律、匀变速运动规律等,几乎每年高考都有涉及。
7.B 根据a=可知,在BC段、CD段的最大速率分别为vBC== m/s、vCD==2 m/s,在BC段、CD段的速率不变,因此在两圆弧段运动的最大速率v=2 m/s,通过两圆弧的时间为t2=+= s,小车从A点以最大速率v0=4 m/s匀速经过一段距离l之后开始减速,恰好到B点时速率为2 m/s,根据匀变速直线运动规律得v2-=-2a1(8 m-l),解得l=5 m,在AB段经历时间t1=+= s,因此总时间为t= s,选项B正确。
8.BD 根据平抛运动规律有h=gt2、R=v0t,若h1=h2,则喷出去的水在空中运动时间相等,所以=,选项A错误;根据平抛运动规律,得=,若v1=v2,化简得=,选项B正确;浇水时水的流量Q=Sv0,其中S是出水口横截面积,浇水一周总水量为V总=Q·=S·v0,若ω1=ω2,v1=v2,则总水量相同,但半径越大,摆放的花盆越多,所以落入每个花盆的水量越小,选项C错误;设每个花盆的直径大小为d,则半径为R的圆上能摆放的盆数为n=,浇水一周总水量V总=Q·=SR,落入每个花盆的水量V0==,若h1=h2,落入每个花盆的水量相同,则ω1=ω2,选项D正确。
教材溯源 本题以盆栽浇水为情境,来源于教材第20页第2题图5-7,在此基础上水管做圆周运动,创设平抛运动与圆周运动相结合的物理模型,综合考查匀速圆周运动的角速度、周期、平抛运动规律等知识。
三年模拟练
1.D 李、杨两人在水平U形赛道运动时,与冰面间的动摩擦因数均为μ,且均以转弯时不侧滑的最大速率运动,则最大静摩擦力提供向心力,有μm1g=m1a=m1,μm2g=m2a=m2,可知两人在圆弧部分的向心加速度大小相等,均为a1=a2=μg,李、杨两人的速率之比为==,故A、C错误;李、杨两人通过的路程之比为==,则所用时间之比为==·=·=,B错误,D正确。
2.A 对筒底的小物块,有f=mRω2,N=mg,当静摩擦力取最大值时,有f=μN,联立解得临界角速度ω=,可知转速增大时,B将先滑动,小物块B将要滑动时的角速度ω=;对小物块A受力分析,有N'=mrω2,f'=mg(点拨:竖直方向静摩擦力等于重力),当静摩擦力等于最大静摩擦力时,有f'=μN',联立解得μ=,所以μ=,A正确。
3.D 根据Fn=mω2r可知,在角速度相同的情况下,半径越大,所需的向心力越大,所以圆盘上最外层的细沙随着角速度的增大最先发生滑动(破题关键)。因为圆盘表面上的细沙有被甩掉,即面积上的细沙发生滑动,剩下未滑动,设未滑动部分的半径为r,则πr2=πR2,解得r=R,在最低点有mg(μ cos θ-sin θ)=mω2r(点拨:细沙在最低点最易发生滑动),解得ω=,D正确。
4.B 设绳长为L,绳子与竖直方向的夹角为δ,则由合力提供向心力得mg tan δ=m(L sin δ+r),化简得=L cos δ+,可知L越大,δ越大;设小球到绳上端的竖直距离为h,则由合力提供向心力得mg tan δ=m(h tan δ+r),化简得=h+,可知δ越大,h越大,选B。
5.D 角速度较小时,a、b两木块所受的静摩擦力提供向心力,对a有fa=3mrω2,对b有fb=2mrω2,则角速度较小时,b的静摩擦力较小,则图线(1)对应木块b,A错误;当角速度达到ω1时,b受的最大静摩擦力提供向心力,有f1=μmg=2mr,角速度继续增大,轻绳上出现弹力,当角速度达到ω2时,a达到最大静摩擦力,设此时轻绳的拉力大小为T,对a、b有T+3μmg=3mr,T+μmg=2mr,解得ω2=2ω1,故C错误;角速度继续增大,绳上拉力增大,a的静摩擦力不变,b所受的静摩擦力减小,当角速度达到ω3时,b所受的静摩擦力为零,设此时绳子拉力大小为T',对a、b有T'+3μmg=3mr,T'=2mr,解得ω3=ω2,故B错误;由上述分析可知ω3=ω2,ω2=2ω1,f1=μmg=2mr,T'=2mr,联立解得T'=6f1,故D正确。
6.答案 (1)2ωL (2) (3)2(m+M)g
解析 (1)转轮1、2通过皮带传动,轮缘各点的线速度大小相等,根据v=ωr
可得,ω与r成反比,所以ω1=2ω
铁球与转轮1同轴转动,角速度相等,可得v1=2ωL
(2)底座对地面无压力,可知杆对底座的弹力竖直向上,且F=Mg
由牛顿第三定律可知,杆对铁球向下的弹力FN=F=Mg
对铁球有FN+mg=m
解得v2=
(3)当铁球运动到最低点时,底座对地面压力最大,对铁球,由牛顿第二定律可得T-mg=
解得T=(2m+M)g
根据牛顿第三定律可知,轻杆对底座的作用力大小为(2m+M)g,方向向下。
对底座,由平衡条件可知,地面对底座的支持力大小为2(m+M)g,所以底座对地面的最大压力为Fm=2(m+M)g
7.答案 (1)0.75 N,方向竖直向下
(2)v=(xE≤0.25 m)
解析 (1)根据平抛运动规律,水平方向有xE=vDt0
竖直方向有h-d=g
解得vD=1 m/s
在D点,设轨道对滑块的作用力方向竖直向下,由牛顿第二定律可得FN+mg=
解得滑块从D点飞出时FN=-0.75 N
即轨道对滑块的力大小为0.75 N,方向竖直向上。
根据牛顿第三定律,滑块对轨道的力大小为0.75 N,方向竖直向下。
(2)设小滑块击中收集框底部的点距离左边框为x,根据平抛运动规律,竖直方向有h=gt2
解得t=0.3 s
水平方向有xE+x=vt
落地时的竖直速度大小为vy=gt=3 m/s
反弹后恰好击中G点,竖直方向有d=vyt'-gt'2
解得向上运动的时间t'=0.1 s(另一根舍去)
水平方向有d-x=vt'
综上可解得v=
要使小滑块进入收集框,临界条件为恰好过H点,竖直方向有h-d=g
水平方向有xE=vt0
又因v=
综上解得xE=0.25 m
故小球从D点飞出的速度大小v与收集框的E点坐标xE之间应满足v=(xE≤0.25 m)
模型分析 本题涉及三个物理模型——平抛运动模型、轻杆模型和斜抛运动模型。
(1)滑块从D点飞出落入收集框EFGH过程做平抛运动,可画出滑块恰好过H的临界轨迹,利用平抛运动的相关规律求解问题;
(2)滑块在圆弧管道的CD部分运动时可类比轻杆模型,利用圆周运动规律求解相关问题;
(3)滑块击中收集框的底部反弹至收集框上的G点过程做斜上抛运动,运用运动的分解知识求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
