2025人教版高中物理必修第二册强化练习题--专题强化练4 圆周运动的动力学问题
文档属性
| 名称 | 2025人教版高中物理必修第二册强化练习题--专题强化练4 圆周运动的动力学问题 |  | |
| 格式 | docx | ||
| 文件大小 | 442.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-06 09:04:12 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025人教版高中物理必修第二册
专题强化练4 圆周运动的动力学问题
一、选择题
1.(2024山东青岛四区期中联考)智能呼啦圈轻便美观,深受大众喜爱。如图甲所示,将带有滑轮的短杆一端穿入腰带外侧轨道,另一端悬挂一根带有配重的轻绳,将腰带水平系在腰间,通过人体扭动,配重会随短杆做水平匀速圆周运动,其简化模型如图乙所示,悬挂点P到腰带中心点O的距离d=0.2 m,绳子与竖直方向的夹角为θ,绳长l=0.5 m,可视为质点的配重质量为m=0.5 kg,重力加速度大小g=10 m/s2,sin 37°=0.6,下列说法正确的是 ( )
A.匀速转动时,配重受到的合力恒定不变
B.增大转速,则身体对腰带的摩擦力变大
C.转动过程中杆的拉力T=mg cos θ
D.当使用者掌握好锻炼节奏后能够使θ稳定在37°,此时配重的角速度ω= rad/s
2.(2024湖南长沙长郡中学月考)如图所示,质量为m的小球套在粗糙直杆上,杆与水平面间始终保持θ=37°角。初始时直杆静止,小球恰好静止在A点,A、M间距为L。现使小球与直杆一起绕经过直杆下端的竖直轴MN以某一角速度ω0匀速转动,小球仍处于A点且与直杆之间的摩擦力恰好为零。重力加速度为g,已知sin 37°=0.6,cos 37°=0.8。则 ( )
A.小球与直杆之间的动摩擦因数为
B.小球的角速度ω0=
C.小球受到的弹力大小为
D.当直杆以角速度ω=转动时,小球受到的摩擦力方向沿杆向上
3.(多选题)(2024山东潍坊期末)通用技术课上,某兴趣小组制作了一个电动爬杆小猴,原理如图所示,竖直杆OM与光滑杆ON均固定在电动机底座上,且ON与水平面的夹角α=60°,一弹簧上端固定在OM杆上的P点,下端与穿在ON杆上质量为m的小猴相连。小猴静止时弹簧轴线与竖直方向的夹角β=30°,当电动机带动底座开始转动时,小猴开始爬杆。已知O、P两点间的距离为L,重力加速度为g。则 ( )
A.小猴静止时杆对小猴的弹力方向垂直于杆ON斜向下
B.小猴静止时弹簧弹力的大小为mg
C.小猴静止时杆对小猴的弹力大小为mg
D.电动机转动后,当小猴稳定在与P点等高的位置时杆的角速度为
二、非选择题
4.(2024山东淄博期中)如图所示,在足够大的转盘中心固定一个小物块B,距离中心为r0=0.2 m处放置小物块A,A、B质量均为m=1 kg,A与转盘之间的动摩擦因数为μ1=0.5,现在用原长为d=0.2 m、劲度系数k=40 N/m的轻质弹簧将两者拴接,重力加速度g=10 m/s2,假设弹簧始终处于弹性限度以内,最大静摩擦力等于滑动摩擦力,则:
(1)缓慢增加转盘转动的角速度,求A即将打滑时转盘的角速度ω0;
(2)若转盘的角速度ω1=6 rad/s,A可以放置在离中心距离不同的位置上,且A始终不打滑,求满足条件的A的转动半径rA的范围。
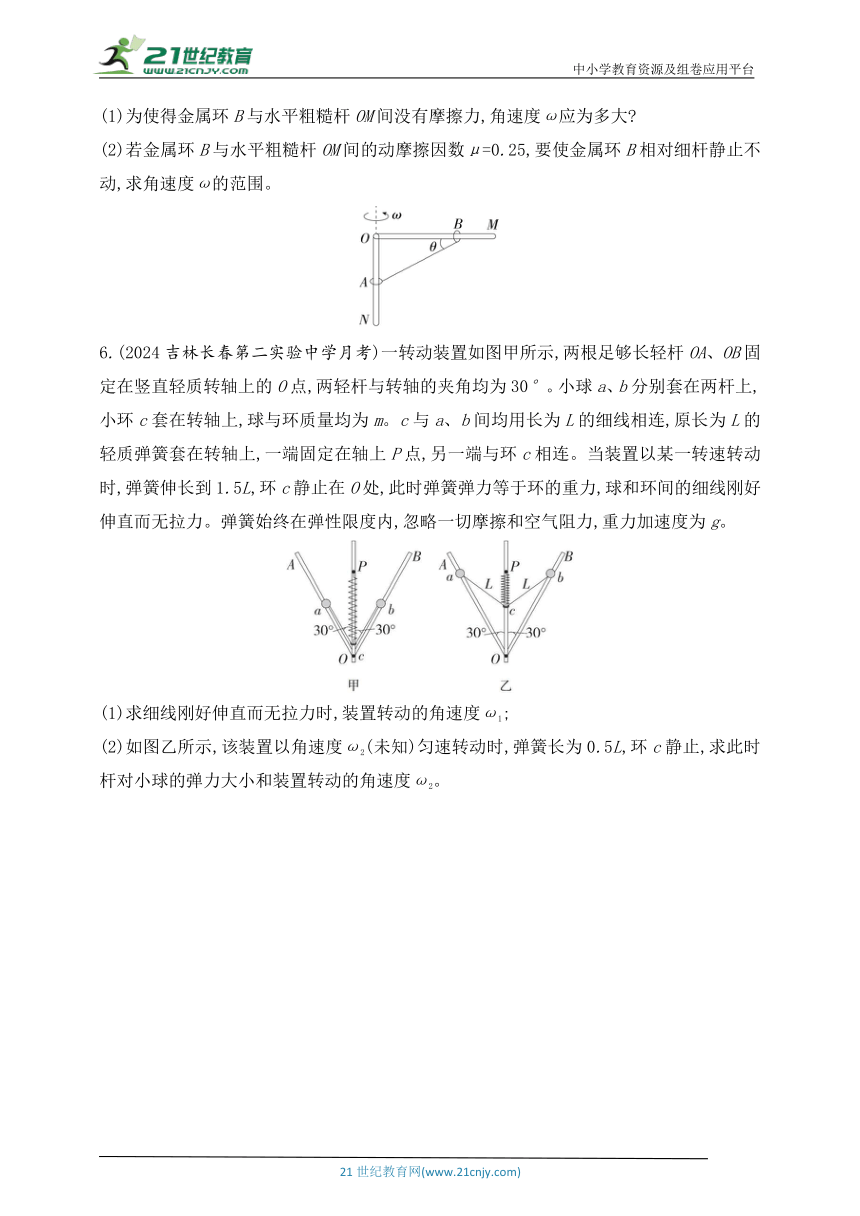
5.(2024河北邢台期中)如图所示,金属环A、B的质量分别为m1=0.6 kg、m2=1 kg,用不可伸长的细线连接,分别套在水平粗糙细杆OM和竖直光滑细杆ON上,B环到竖直杆O点的距离为L=1 m,细线与水平杆OM的夹角θ=37°。当整个装置以竖直杆ON为轴以不同大小的角速度ω匀速转动时,两金属环一直相对杆不动。已知环与杆间的最大静摩擦力等于滑动摩擦力,重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8。
(1)为使得金属环B与水平粗糙杆OM间没有摩擦力,角速度ω应为多大
(2)若金属环B与水平粗糙杆OM间的动摩擦因数μ=0.25,要使金属环B相对细杆静止不动,求角速度ω的范围。
6.(2024吉林长春第二实验中学月考)一转动装置如图甲所示,两根足够长轻杆OA、OB固定在竖直轻质转轴上的O点,两轻杆与转轴的夹角均为30°。小球a、b分别套在两杆上,小环c套在转轴上,球与环质量均为m。c与a、b间均用长为L的细线相连,原长为L的轻质弹簧套在转轴上,一端固定在轴上P点,另一端与环c相连。当装置以某一转速转动时,弹簧伸长到1.5L,环c静止在O处,此时弹簧弹力等于环的重力,球和环间的细线刚好伸直而无拉力。弹簧始终在弹性限度内,忽略一切摩擦和空气阻力,重力加速度为g。
(1)求细线刚好伸直而无拉力时,装置转动的角速度ω1;
(2)如图乙所示,该装置以角速度ω2(未知)匀速转动时,弹簧长为0.5L,环c静止,求此时杆对小球的弹力大小和装置转动的角速度ω2。
答案与分层梯度式解析
专题强化练4 圆周运动的动力学问题
1.D 匀速转动时,配重受到的合力提供向心力,其大小不变,方向变化,A错误。配重匀速转动时,其受力如图所示,在竖直方向有mg=T cos θ,则T=,水平方向有T sin θ=m(2πn)2r,若增大转速,配重做匀速圆周运动的半径变大,短杆与竖直方向的夹角θ将增大,对腰带有f=Mg+T cos θ=Mg+mg(设腰带的质量为M,人对腰带的摩擦力为f),则拉力T变大,向心力变大,f不变,即身体对腰带的摩擦力不变,B、C错误。当θ稳定在37°时,对配重,根据牛顿第二定律可得mg tan θ=mω2(l sin θ+d),解得ω= rad/s,D正确。
2.B 直杆静止,小球恰好静止在A点时,由平衡条件得mg sin 37°=μmg cos 37°,解得小球与直杆之间的动摩擦因数μ=,A错误;小球与直杆一起以角速度ω0匀速转动时,摩擦力为零,支持力和重力的合力提供向心力,如图所示,有FN==,mg tan 37°=m·L cos 37°,解得ω0=,B正确,C错误;当小球的角速度ω=时,重力和支持力的合力不足以提供向心力(点拨:需要摩擦力提供一部分向心力),摩擦力方向沿杆向下,D错误。
3.AD 对小猴受力分析如图甲所示,由平衡条件可知,小猴静止时杆对小猴的弹力方向垂直于杆ON斜向下(点拨:三个平衡的共点力一定不在一直线的同侧),A正确;小猴静止时弹簧弹力的大小为Fk=2mg cos β=mg,杆对小猴的弹力大小为FN=mg,故B、C错误;当小猴稳定在与P点等高的位置时,如图乙所示,由几何关系可知,弹簧的长度与小猴静止时相等,故弹簧的弹力为F'k=Fk=mg,在P点,对小猴受力分析,水平方向由牛顿第二定律有F'k+F'N cos 30°=mL tan 30°·ω2,竖直方向由平衡条件可得F'N sin 30°=mg,联立解得ω=,D正确。
思路强化
匀速圆周运动问题的解题策略
(1)分解力:将物体所受外力分解到互相垂直的两个方向上,其中一个方向沿圆周运动的半径方向,另一个方向沿垂直半径方向。
(2)列方程:沿半径方向满足F合1=mrω2=m=mr,沿垂直半径方向满足F合2=0。
4.答案 (1)5 rad/s (2)0.75 m≤rA≤3.25 m
关键点拨 解答本题的关键是要明确:一、弹簧处于原长时,物块A的向心力由摩擦力提供;二、A恰好不打滑的临界条件是A所受的摩擦力达到最大静摩擦力。
解析 (1)由于A距离转盘中心r0=0.2 m,恰好等于弹簧原长,则物块A即将打滑时,由最大静摩擦力提供向心力,即有μ1mg=mr0
解得A即将打滑时转盘的角速度ω0=5 rad/s
(2)A放置在离转盘中心距离不同的位置上时弹簧的弹力不同,由于ω1=6 rad/s>ω0,知弹簧处于伸长状态。(破题关键)由临界条件可得,当摩擦力指向圆心时,F1+f=mr1
当摩擦力背离圆心时,F2-f=mr2
其中f=μ1mg
由胡克定律可知F1=k(r1-r0)
F2=k(r2-r0)
代入数值解得r1=0.75 m,r2=3.25 m
故满足条件的A的转动半径rA的范围为0.75 m≤rA≤3.25 m。
5.答案 (1)2 rad/s (2)2 rad/s≤ω≤2 rad/s
解析 (1)设细线张力大小为T,对于A环有m1g=T sin θ
当金属环B与水平粗糙杆OM间没有摩擦力时,细线对金属环B的拉力沿MO方向的分力恰好提供了金属环B所需的向心力,即T cos θ=m2ω2L
联立解得ω==2 rad/s
(2)金属环B与水平粗糙杆间的最大静摩擦力为
f=μ(m2g+T sin θ)=4 N
细线对金属环B的拉力沿MO方向的分力为
TMO=T cos θ=8 N>f
所以角速度ω=0时金属环B相对于细杆不能保持静止。
设角速度最小为ω1时金属环B恰能相对于细杆保持静止,则有T cos θ-f=m2L
解得ω1=2 rad/s
设角速度最大为ω2时金属环B恰能相对于细杆保持静止,则有T cos θ+f=m2L
解得ω2=2 rad/s
所以角速度ω的范围为2 rad/s≤ω≤2 rad/s。
6.答案 (1) (2)4mg
解析 (1)细线刚好伸直而无拉力时,对a或b小球受力分析,根据牛顿第二定律得=mL sin 30°
解得ω1=
(2)依题可知,两次弹簧弹力大小相等方向相反,故此时弹簧弹力的大小为F1=mg(点拨:弹簧拉伸和压缩的形变量相同)
设细线的拉力大小为F2,细线与竖直轴的夹角为60°,对c环分析,根据平衡条件得
2F2 cos 60°=mg+F1
解得F2=2mg
对a球分析,在竖直方向,根据平衡条件得
FN sin 30°=mg+F2 cos 60°
解得FN=4mg
在水平方向,根据牛顿第二定律得
FN cos 30°+F2 sin 60°=mL sin 60°
解得ω2=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教版高中物理必修第二册
专题强化练4 圆周运动的动力学问题
一、选择题
1.(2024山东青岛四区期中联考)智能呼啦圈轻便美观,深受大众喜爱。如图甲所示,将带有滑轮的短杆一端穿入腰带外侧轨道,另一端悬挂一根带有配重的轻绳,将腰带水平系在腰间,通过人体扭动,配重会随短杆做水平匀速圆周运动,其简化模型如图乙所示,悬挂点P到腰带中心点O的距离d=0.2 m,绳子与竖直方向的夹角为θ,绳长l=0.5 m,可视为质点的配重质量为m=0.5 kg,重力加速度大小g=10 m/s2,sin 37°=0.6,下列说法正确的是 ( )
A.匀速转动时,配重受到的合力恒定不变
B.增大转速,则身体对腰带的摩擦力变大
C.转动过程中杆的拉力T=mg cos θ
D.当使用者掌握好锻炼节奏后能够使θ稳定在37°,此时配重的角速度ω= rad/s
2.(2024湖南长沙长郡中学月考)如图所示,质量为m的小球套在粗糙直杆上,杆与水平面间始终保持θ=37°角。初始时直杆静止,小球恰好静止在A点,A、M间距为L。现使小球与直杆一起绕经过直杆下端的竖直轴MN以某一角速度ω0匀速转动,小球仍处于A点且与直杆之间的摩擦力恰好为零。重力加速度为g,已知sin 37°=0.6,cos 37°=0.8。则 ( )
A.小球与直杆之间的动摩擦因数为
B.小球的角速度ω0=
C.小球受到的弹力大小为
D.当直杆以角速度ω=转动时,小球受到的摩擦力方向沿杆向上
3.(多选题)(2024山东潍坊期末)通用技术课上,某兴趣小组制作了一个电动爬杆小猴,原理如图所示,竖直杆OM与光滑杆ON均固定在电动机底座上,且ON与水平面的夹角α=60°,一弹簧上端固定在OM杆上的P点,下端与穿在ON杆上质量为m的小猴相连。小猴静止时弹簧轴线与竖直方向的夹角β=30°,当电动机带动底座开始转动时,小猴开始爬杆。已知O、P两点间的距离为L,重力加速度为g。则 ( )
A.小猴静止时杆对小猴的弹力方向垂直于杆ON斜向下
B.小猴静止时弹簧弹力的大小为mg
C.小猴静止时杆对小猴的弹力大小为mg
D.电动机转动后,当小猴稳定在与P点等高的位置时杆的角速度为
二、非选择题
4.(2024山东淄博期中)如图所示,在足够大的转盘中心固定一个小物块B,距离中心为r0=0.2 m处放置小物块A,A、B质量均为m=1 kg,A与转盘之间的动摩擦因数为μ1=0.5,现在用原长为d=0.2 m、劲度系数k=40 N/m的轻质弹簧将两者拴接,重力加速度g=10 m/s2,假设弹簧始终处于弹性限度以内,最大静摩擦力等于滑动摩擦力,则:
(1)缓慢增加转盘转动的角速度,求A即将打滑时转盘的角速度ω0;
(2)若转盘的角速度ω1=6 rad/s,A可以放置在离中心距离不同的位置上,且A始终不打滑,求满足条件的A的转动半径rA的范围。
5.(2024河北邢台期中)如图所示,金属环A、B的质量分别为m1=0.6 kg、m2=1 kg,用不可伸长的细线连接,分别套在水平粗糙细杆OM和竖直光滑细杆ON上,B环到竖直杆O点的距离为L=1 m,细线与水平杆OM的夹角θ=37°。当整个装置以竖直杆ON为轴以不同大小的角速度ω匀速转动时,两金属环一直相对杆不动。已知环与杆间的最大静摩擦力等于滑动摩擦力,重力加速度g取10 m/s2,sin 37°=0.6,cos 37°=0.8。
(1)为使得金属环B与水平粗糙杆OM间没有摩擦力,角速度ω应为多大
(2)若金属环B与水平粗糙杆OM间的动摩擦因数μ=0.25,要使金属环B相对细杆静止不动,求角速度ω的范围。
6.(2024吉林长春第二实验中学月考)一转动装置如图甲所示,两根足够长轻杆OA、OB固定在竖直轻质转轴上的O点,两轻杆与转轴的夹角均为30°。小球a、b分别套在两杆上,小环c套在转轴上,球与环质量均为m。c与a、b间均用长为L的细线相连,原长为L的轻质弹簧套在转轴上,一端固定在轴上P点,另一端与环c相连。当装置以某一转速转动时,弹簧伸长到1.5L,环c静止在O处,此时弹簧弹力等于环的重力,球和环间的细线刚好伸直而无拉力。弹簧始终在弹性限度内,忽略一切摩擦和空气阻力,重力加速度为g。
(1)求细线刚好伸直而无拉力时,装置转动的角速度ω1;
(2)如图乙所示,该装置以角速度ω2(未知)匀速转动时,弹簧长为0.5L,环c静止,求此时杆对小球的弹力大小和装置转动的角速度ω2。
答案与分层梯度式解析
专题强化练4 圆周运动的动力学问题
1.D 匀速转动时,配重受到的合力提供向心力,其大小不变,方向变化,A错误。配重匀速转动时,其受力如图所示,在竖直方向有mg=T cos θ,则T=,水平方向有T sin θ=m(2πn)2r,若增大转速,配重做匀速圆周运动的半径变大,短杆与竖直方向的夹角θ将增大,对腰带有f=Mg+T cos θ=Mg+mg(设腰带的质量为M,人对腰带的摩擦力为f),则拉力T变大,向心力变大,f不变,即身体对腰带的摩擦力不变,B、C错误。当θ稳定在37°时,对配重,根据牛顿第二定律可得mg tan θ=mω2(l sin θ+d),解得ω= rad/s,D正确。
2.B 直杆静止,小球恰好静止在A点时,由平衡条件得mg sin 37°=μmg cos 37°,解得小球与直杆之间的动摩擦因数μ=,A错误;小球与直杆一起以角速度ω0匀速转动时,摩擦力为零,支持力和重力的合力提供向心力,如图所示,有FN==,mg tan 37°=m·L cos 37°,解得ω0=,B正确,C错误;当小球的角速度ω=时,重力和支持力的合力不足以提供向心力(点拨:需要摩擦力提供一部分向心力),摩擦力方向沿杆向下,D错误。
3.AD 对小猴受力分析如图甲所示,由平衡条件可知,小猴静止时杆对小猴的弹力方向垂直于杆ON斜向下(点拨:三个平衡的共点力一定不在一直线的同侧),A正确;小猴静止时弹簧弹力的大小为Fk=2mg cos β=mg,杆对小猴的弹力大小为FN=mg,故B、C错误;当小猴稳定在与P点等高的位置时,如图乙所示,由几何关系可知,弹簧的长度与小猴静止时相等,故弹簧的弹力为F'k=Fk=mg,在P点,对小猴受力分析,水平方向由牛顿第二定律有F'k+F'N cos 30°=mL tan 30°·ω2,竖直方向由平衡条件可得F'N sin 30°=mg,联立解得ω=,D正确。
思路强化
匀速圆周运动问题的解题策略
(1)分解力:将物体所受外力分解到互相垂直的两个方向上,其中一个方向沿圆周运动的半径方向,另一个方向沿垂直半径方向。
(2)列方程:沿半径方向满足F合1=mrω2=m=mr,沿垂直半径方向满足F合2=0。
4.答案 (1)5 rad/s (2)0.75 m≤rA≤3.25 m
关键点拨 解答本题的关键是要明确:一、弹簧处于原长时,物块A的向心力由摩擦力提供;二、A恰好不打滑的临界条件是A所受的摩擦力达到最大静摩擦力。
解析 (1)由于A距离转盘中心r0=0.2 m,恰好等于弹簧原长,则物块A即将打滑时,由最大静摩擦力提供向心力,即有μ1mg=mr0
解得A即将打滑时转盘的角速度ω0=5 rad/s
(2)A放置在离转盘中心距离不同的位置上时弹簧的弹力不同,由于ω1=6 rad/s>ω0,知弹簧处于伸长状态。(破题关键)由临界条件可得,当摩擦力指向圆心时,F1+f=mr1
当摩擦力背离圆心时,F2-f=mr2
其中f=μ1mg
由胡克定律可知F1=k(r1-r0)
F2=k(r2-r0)
代入数值解得r1=0.75 m,r2=3.25 m
故满足条件的A的转动半径rA的范围为0.75 m≤rA≤3.25 m。
5.答案 (1)2 rad/s (2)2 rad/s≤ω≤2 rad/s
解析 (1)设细线张力大小为T,对于A环有m1g=T sin θ
当金属环B与水平粗糙杆OM间没有摩擦力时,细线对金属环B的拉力沿MO方向的分力恰好提供了金属环B所需的向心力,即T cos θ=m2ω2L
联立解得ω==2 rad/s
(2)金属环B与水平粗糙杆间的最大静摩擦力为
f=μ(m2g+T sin θ)=4 N
细线对金属环B的拉力沿MO方向的分力为
TMO=T cos θ=8 N>f
所以角速度ω=0时金属环B相对于细杆不能保持静止。
设角速度最小为ω1时金属环B恰能相对于细杆保持静止,则有T cos θ-f=m2L
解得ω1=2 rad/s
设角速度最大为ω2时金属环B恰能相对于细杆保持静止,则有T cos θ+f=m2L
解得ω2=2 rad/s
所以角速度ω的范围为2 rad/s≤ω≤2 rad/s。
6.答案 (1) (2)4mg
解析 (1)细线刚好伸直而无拉力时,对a或b小球受力分析,根据牛顿第二定律得=mL sin 30°
解得ω1=
(2)依题可知,两次弹簧弹力大小相等方向相反,故此时弹簧弹力的大小为F1=mg(点拨:弹簧拉伸和压缩的形变量相同)
设细线的拉力大小为F2,细线与竖直轴的夹角为60°,对c环分析,根据平衡条件得
2F2 cos 60°=mg+F1
解得F2=2mg
对a球分析,在竖直方向,根据平衡条件得
FN sin 30°=mg+F2 cos 60°
解得FN=4mg
在水平方向,根据牛顿第二定律得
FN cos 30°+F2 sin 60°=mL sin 60°
解得ω2=
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
