第二十四章圆同步练习(含答案) 2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 第二十四章圆同步练习(含答案) 2024-2025学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 615.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-04 20:02:04 | ||
图片预览


文档简介
第二十四章圆同步练习 2024-2025学年人教版数学九年级上册
一、单选题
1.用反证法证明“中至少有两个锐角”,第一步应为( )
A.假设中至多有一个锐角 B.假设中有一个直角
C.假设中有两个直角 D.假设中有两个锐角
2.如图,为外一点,、分别切于、,切于点,分别交、于点、,若,则的周长为( )
A.5 B.10 C.15 D.20
3.如图,点A,B,C在⊙O上,AB∥CO,∠B=22°,则∠A=( ).
A.22° B.40° C.44° D.68°
4.如图是长沙某4S店新能源车轮胎展厅陈列的轮胎正面及其固定支架的截面图,凹槽是矩形.当轮胎正立且紧靠支架于点A,D时,恰好与边相切.若,,则此轮胎的半径为( )
A. B. C. D.
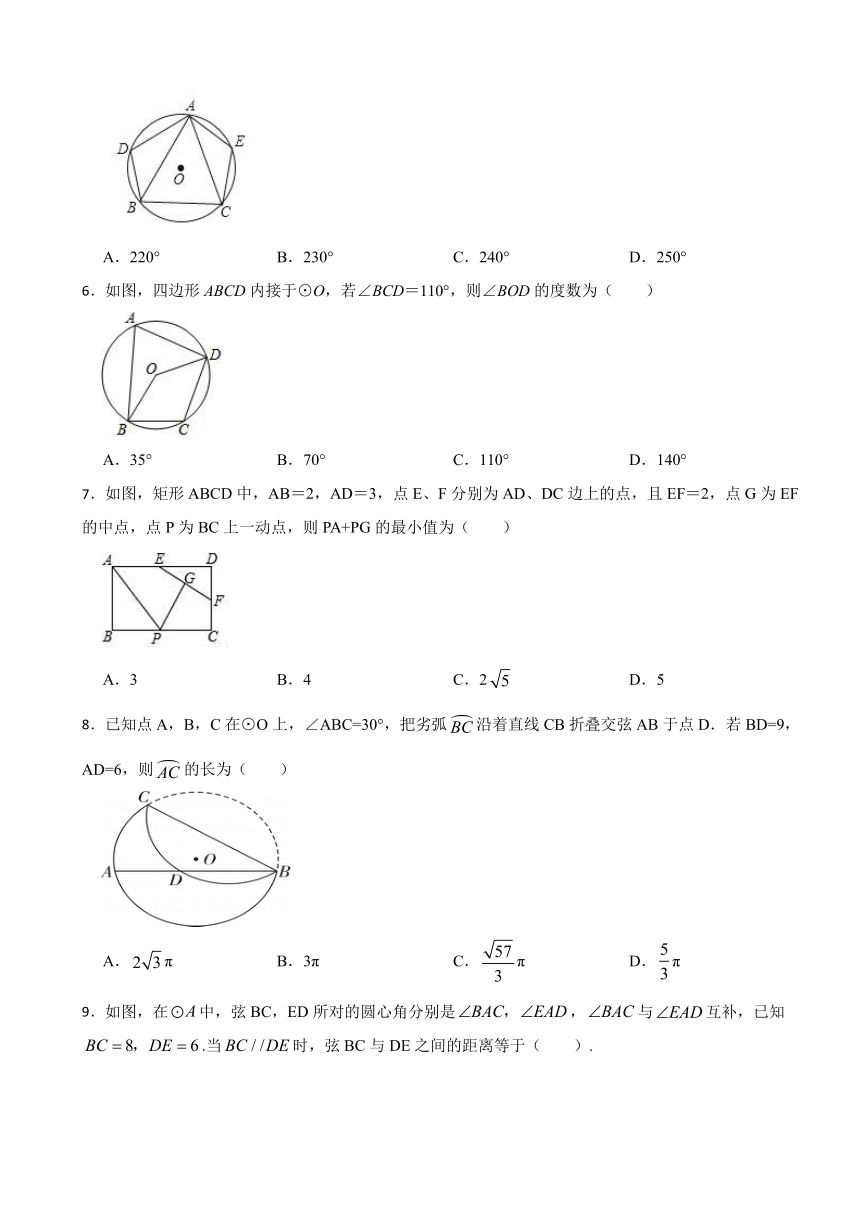
5.如图所示,△ABC的三个顶点在⊙O上,D是上的点,E是上的点,若∠BAC=50°.则∠D+∠E=( )
A.220° B.230° C.240° D.250°
6.如图,四边形ABCD内接于⊙O,若∠BCD=110°,则∠BOD的度数为( )
A.35° B.70° C.110° D.140°
7.如图,矩形ABCD中,AB=2,AD=3,点E、F分别为AD、DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为( )
A.3 B.4 C.2 D.5
8.已知点A,B,C在⊙O上,∠ABC=30°,把劣弧沿着直线CB折叠交弦AB于点D.若BD=9,AD=6,则的长为( )
A.π B.3π C.π D.π
9.如图,在中,弦BC,ED所对的圆心角分别是,与互补,已知.当时,弦BC与DE之间的距离等于( ).
A.7 B.1或7
C. D.或
10.在Rt△ABC中,∠C=90°,AC=10,BC=12,点D为线段BC上一动点.以CD为⊙O直径,作AD交⊙O于点E,则BE的最小值为( )
A.6 B.8 C.10 D.12
二、填空题
11.半径为4cm,圆心角为60°的扇形的面积为 cm2.
12.如图,点A,B,C,D,E都在上,,,则 .
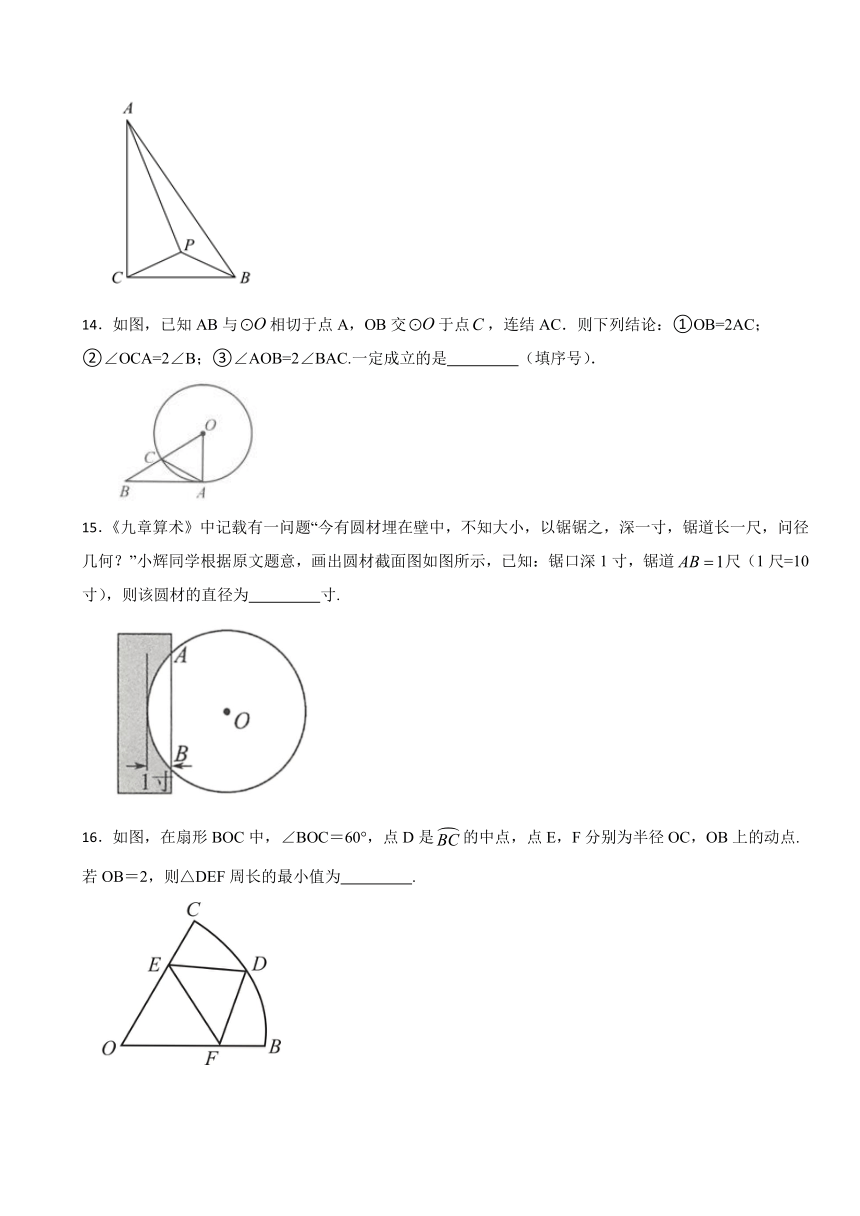
13.如图,在 中, , , ,P是 所在平面内一点,且满足 ,则 的最大值为 .
14.如图,已知AB与相切于点A,OB交于点,连结AC.则下列结论:①OB=2AC;②∠OCA=2∠B;③∠AOB=2∠BAC.一定成立的是 (填序号).
15.《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深1寸,锯道尺(1尺=10寸),则该圆材的直径为 寸.
16.如图,在扇形BOC中,∠BOC=60°,点D是的中点,点E,F分别为半径OC,OB上的动点.若OB=2,则△DEF周长的最小值为 .
三、解答题
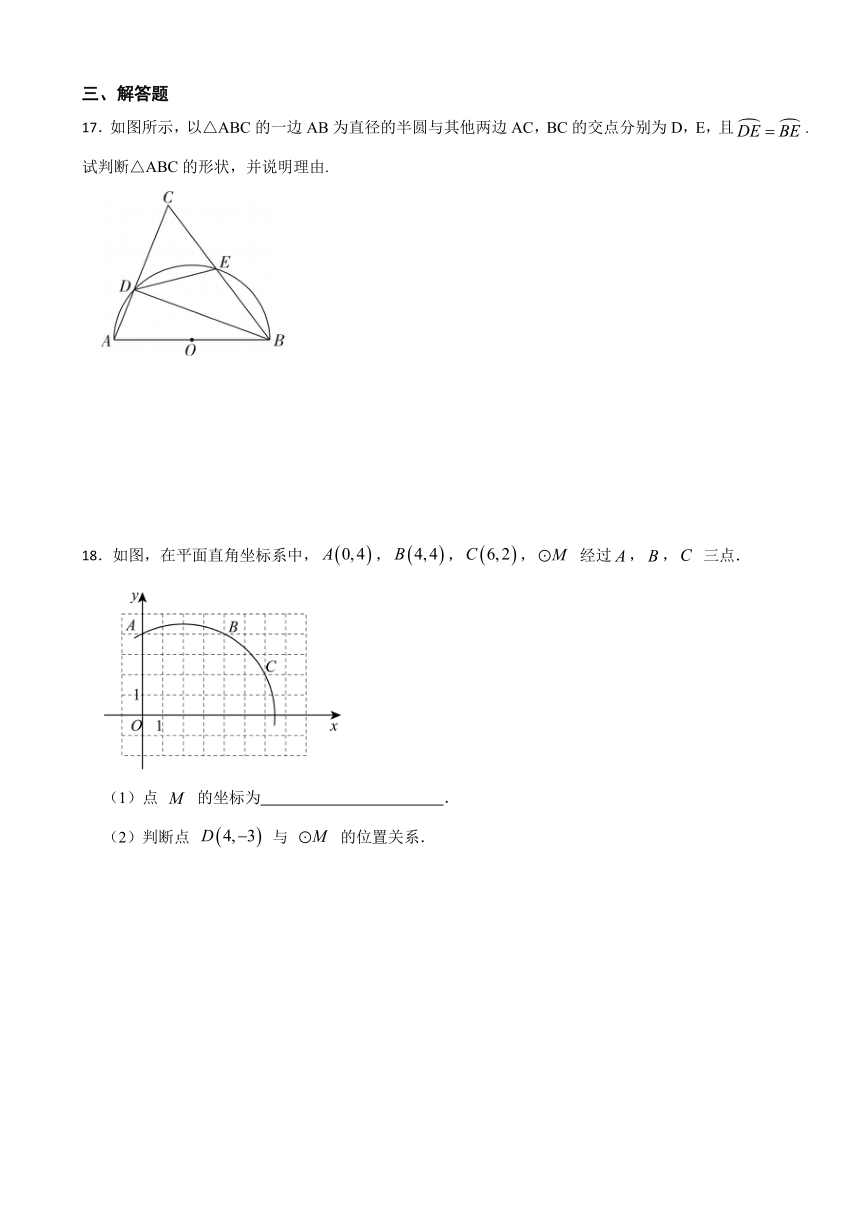
17.如图所示,以△ABC的一边AB为直径的半圆与其他两边AC,BC的交点分别为D,E,且.试判断△ABC的形状,并说明理由.
18.如图,在平面直角坐标系中,,,, 经过,, 三点.
(1)点 的坐标为 .
(2)判断点 与 的位置关系.
19.如图AB是⊙O的直径,弦CD⊥AB于点E,若EB=9,AE=1,求弦CD的长.
20. 如图, 内接于 交 于点 交 于点 , 交 于点 , 连结 .
(1)求证: .
(2) 若 的半径为 , 求 的长 (结果保留 ).
21.如图,直径是50cm圆柱形油槽装入油后,油深CD为15cm,求油面宽度AB
22.已知,直角中,,,,过,两点作圆交射线于点,交射线于点.
(1)如图1,当点在线段中点时,求的长;
(2)如图2,当点在线段上时,若点为中点,求的长;
(3)如图3,连接,若为等腰三角形,求所有满足条件的的值.
答案解析部分
1.A
2.B
3.C
4.C
5.B
6.D
7.B
8.C
9.B
10.B
11. π
12.
13. +2
14.③
15.26
16.
17.解:△ABC是腰三角形,理由如下:如图,连接AE,
∵AB是半圆的直径,
∴∠AEB=∠AEC=90°,
∵弧DE=弧BE,
∴∠CAE=∠BAE,
又∵AE=AE,
∴△AEB≌△AEC(ASA),
∴AB=AC,
∴△ABC是腰三角形.
18.(1)
(2)点在内
19.解:连接OC,如图,
∵CD⊥AB,
∴CE=DE,
∵EB=9,AE=1,
∴AB=10,OC=OA=5,
∴OE=4,
在Rt△OCE中,CE= ,
∴CD=2CE=6.
20.(1)证明:
四边形 ADEB 为平行四边形,
.
(2)解:连结 OC、OA, 如图所示.
由(1) 得
的长 .
21..
22.(1);
(2);
(3),,;
一、单选题
1.用反证法证明“中至少有两个锐角”,第一步应为( )
A.假设中至多有一个锐角 B.假设中有一个直角
C.假设中有两个直角 D.假设中有两个锐角
2.如图,为外一点,、分别切于、,切于点,分别交、于点、,若,则的周长为( )
A.5 B.10 C.15 D.20
3.如图,点A,B,C在⊙O上,AB∥CO,∠B=22°,则∠A=( ).
A.22° B.40° C.44° D.68°
4.如图是长沙某4S店新能源车轮胎展厅陈列的轮胎正面及其固定支架的截面图,凹槽是矩形.当轮胎正立且紧靠支架于点A,D时,恰好与边相切.若,,则此轮胎的半径为( )
A. B. C. D.
5.如图所示,△ABC的三个顶点在⊙O上,D是上的点,E是上的点,若∠BAC=50°.则∠D+∠E=( )
A.220° B.230° C.240° D.250°
6.如图,四边形ABCD内接于⊙O,若∠BCD=110°,则∠BOD的度数为( )
A.35° B.70° C.110° D.140°
7.如图,矩形ABCD中,AB=2,AD=3,点E、F分别为AD、DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为( )
A.3 B.4 C.2 D.5
8.已知点A,B,C在⊙O上,∠ABC=30°,把劣弧沿着直线CB折叠交弦AB于点D.若BD=9,AD=6,则的长为( )
A.π B.3π C.π D.π
9.如图,在中,弦BC,ED所对的圆心角分别是,与互补,已知.当时,弦BC与DE之间的距离等于( ).
A.7 B.1或7
C. D.或
10.在Rt△ABC中,∠C=90°,AC=10,BC=12,点D为线段BC上一动点.以CD为⊙O直径,作AD交⊙O于点E,则BE的最小值为( )
A.6 B.8 C.10 D.12
二、填空题
11.半径为4cm,圆心角为60°的扇形的面积为 cm2.
12.如图,点A,B,C,D,E都在上,,,则 .
13.如图,在 中, , , ,P是 所在平面内一点,且满足 ,则 的最大值为 .
14.如图,已知AB与相切于点A,OB交于点,连结AC.则下列结论:①OB=2AC;②∠OCA=2∠B;③∠AOB=2∠BAC.一定成立的是 (填序号).
15.《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深1寸,锯道尺(1尺=10寸),则该圆材的直径为 寸.
16.如图,在扇形BOC中,∠BOC=60°,点D是的中点,点E,F分别为半径OC,OB上的动点.若OB=2,则△DEF周长的最小值为 .
三、解答题
17.如图所示,以△ABC的一边AB为直径的半圆与其他两边AC,BC的交点分别为D,E,且.试判断△ABC的形状,并说明理由.
18.如图,在平面直角坐标系中,,,, 经过,, 三点.
(1)点 的坐标为 .
(2)判断点 与 的位置关系.
19.如图AB是⊙O的直径,弦CD⊥AB于点E,若EB=9,AE=1,求弦CD的长.
20. 如图, 内接于 交 于点 交 于点 , 交 于点 , 连结 .
(1)求证: .
(2) 若 的半径为 , 求 的长 (结果保留 ).
21.如图,直径是50cm圆柱形油槽装入油后,油深CD为15cm,求油面宽度AB
22.已知,直角中,,,,过,两点作圆交射线于点,交射线于点.
(1)如图1,当点在线段中点时,求的长;
(2)如图2,当点在线段上时,若点为中点,求的长;
(3)如图3,连接,若为等腰三角形,求所有满足条件的的值.
答案解析部分
1.A
2.B
3.C
4.C
5.B
6.D
7.B
8.C
9.B
10.B
11. π
12.
13. +2
14.③
15.26
16.
17.解:△ABC是腰三角形,理由如下:如图,连接AE,
∵AB是半圆的直径,
∴∠AEB=∠AEC=90°,
∵弧DE=弧BE,
∴∠CAE=∠BAE,
又∵AE=AE,
∴△AEB≌△AEC(ASA),
∴AB=AC,
∴△ABC是腰三角形.
18.(1)
(2)点在内
19.解:连接OC,如图,
∵CD⊥AB,
∴CE=DE,
∵EB=9,AE=1,
∴AB=10,OC=OA=5,
∴OE=4,
在Rt△OCE中,CE= ,
∴CD=2CE=6.
20.(1)证明:
四边形 ADEB 为平行四边形,
.
(2)解:连结 OC、OA, 如图所示.
由(1) 得
的长 .
21..
22.(1);
(2);
(3),,;
同课章节目录
