青岛版五年级上册数学-五《梯形的面积》课件(共17张PPT)
文档属性
| 名称 | 青岛版五年级上册数学-五《梯形的面积》课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-04 11:02:19 | ||
图片预览


文档简介
(共17张PPT)
梯形的面积
青岛版(六年制) 数学 五年级 上册
多边形的面积
五
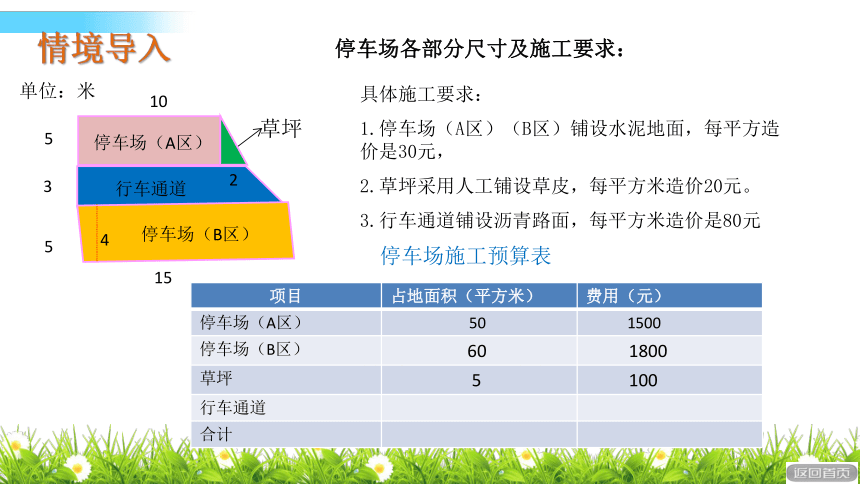
具体施工要求:
1.停车场(A区)(B区)铺设水泥地面,每平方造价是30元,
2.草坪采用人工铺设草皮,每平方米造价20元。
3.行车通道铺设沥青路面,每平方米造价是80元
停车场施工预算表
停车施工预算表
停车场各部分尺寸及施工要求:
项目 占地面积(平方米) 费用(元)
停车场(A区) 50 1500
停车场(B区) 60 1800
草坪 5 100
行车通道
合计
草坪
10
5
单位:米
情境导入
停车场(A区)
行车通道
2
3
5
15
停车场(B区)
4
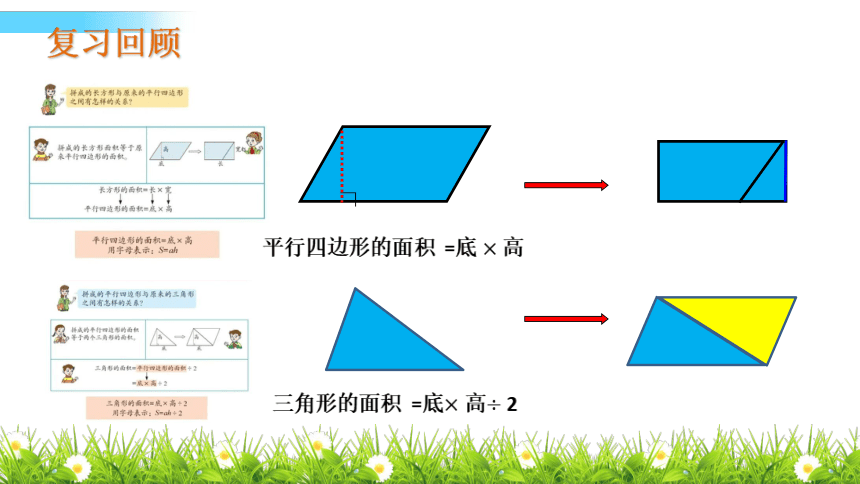
复习回顾
∟
平行四边形的面积 =底 高
三角形的面积 =底 高 2
合作探索
1. 先独立思考,能把梯形转化成学过的什么图形。
2.想一想梯形和转化后的图形有什么关系。
3.把你的方法与小组成员交流,试着推导出梯形的面积计算公式。
活动要求:
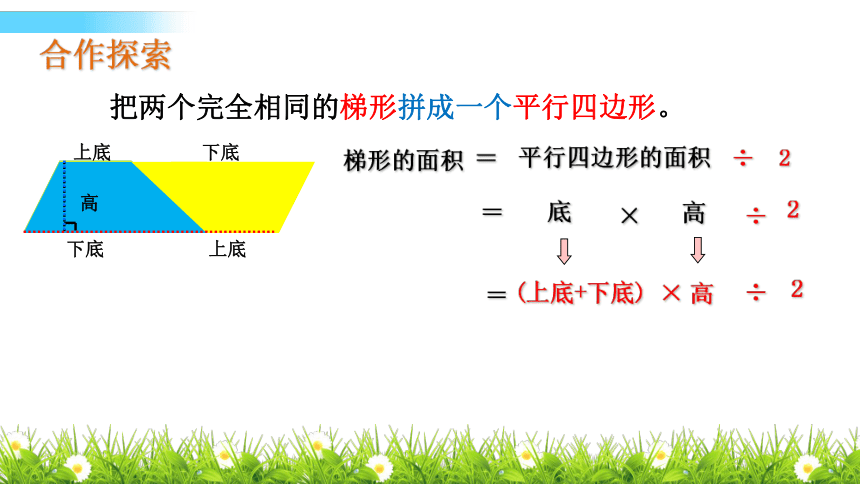
把两个完全相同的梯形拼成一个平行四边形。
梯形的面积
平行四边形的面积
=
底
×
高
(上底+下底)
×
=
高
÷
2
下底
上底
高
下底
上底
合作探索
÷
2
2
÷
=
上底
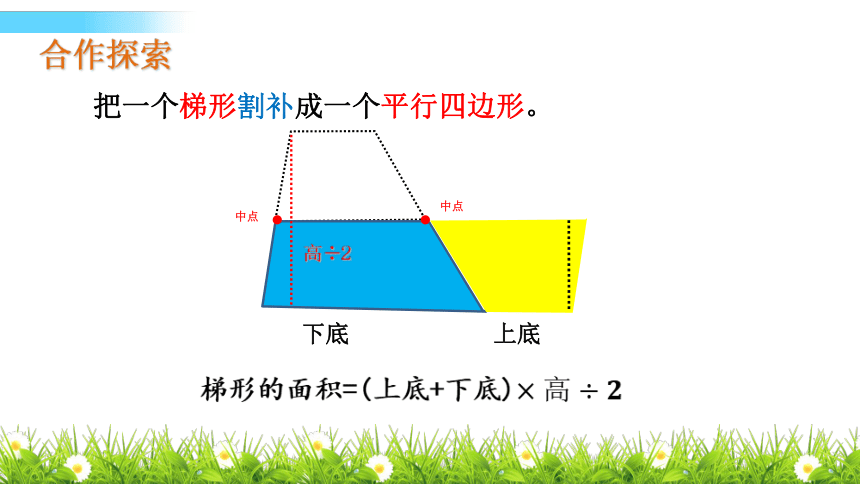
把一个梯形割补成一个平行四边形。
合作探索
梯形的面积=(上底+下底)
高÷2
中点
中点
下底
刘徽,三国时期魏国数学家,被称为“中国古代的数学泰斗”,
他最早利用出入相补的原理来计
算平面图形的面积。
数学文化
刘徽,三国时期魏国数学家,被称为“中国古代的数学泰斗”,
他最早利用出入相补的原理来计
算平面图形的面积。
梯形的面积 =(上底 +下底) 高 2
梯形的面积 =(上底 +下底) 高 2
= 两个三角形的面积之和
= 上底 高2+下底高2
梯形的面积
把一个梯形分割成两个三角形。
1
2
=(上底 +下底) 高 2
合作探索
梯形的面积 =(上底 +下底) 高 2
梯形的面积 =(上底 +下底) 高 2
1
2
梯形的面积 = 上底 高2+下底高2
=(上底 +下底) 高 2
b
h
a
梯形的面积 =(上底 +下底) 高 2
S=(a+b) h 2
这些推导过程有什么相同和不同之处?
具体施工要求:
1.停车场(A区)(B区)铺设水泥地面,每平方造价是30元,
2.草坪采用人工铺设草皮,每平方米造价20元。
3.行车通道铺设沥青路面,每平方米造价是80元
停车场施工预算表
停车施工预算表
停车场各部分尺寸及施工要求:
项目 占地面积(平方米) 费用(元)
停车场(A区) 50 1500
停车场(B区) 60 1800
草坪 5 100
行车通道
合计
草坪
10
5
单位:米
基础练习
停车场(A区)
行车通道
2
3
5
15
停车场(B区)
4
37.5
3000
8cm
12cm
100
基础练习
已知梯形的上底是8厘米,下底是12厘米,
面积是100平方厘米,梯形的高是多少厘米?
(1002)(8+12)
=20020
=10(cm)
答:梯形的高是10厘米。
(3+7)×5÷2
= 10 ×5÷2
=25(根)
答:这堆木材共有25根
木材场常常把木材堆成下图形状。算出图中木材的根数,并用梯形的面积公式解释算法。
拓展应用
总根数 =(顶层根数+底层根数)层数 2
3 根
7 根
5 层
7 根
3 根
自主探索 观察下面的图形你有什么发现?
10cm
6cm
10cm
6cm
2cm
10cm
6cm
5cm
10cm
6cm
梯形的面积=(上底+下底)×高÷2
平行四边形的面积=底×高
三角形的面积=底×高÷2
上底=下底
上底=0
转化
总结提升
梯形的面积=(上底+下底) 高 2
......
1.基础性作业:课本自主练习2、5题;
2.实践性作业:你能设计
课后作业
1.基础性作业:课本自主练习2、5题。
2.实践性作业:寻找生活中形状是梯形的物体,测量出它的相关数据,并计算出它的面积。
梯形的面积
青岛版(六年制) 数学 五年级 上册
多边形的面积
五
具体施工要求:
1.停车场(A区)(B区)铺设水泥地面,每平方造价是30元,
2.草坪采用人工铺设草皮,每平方米造价20元。
3.行车通道铺设沥青路面,每平方米造价是80元
停车场施工预算表
停车施工预算表
停车场各部分尺寸及施工要求:
项目 占地面积(平方米) 费用(元)
停车场(A区) 50 1500
停车场(B区) 60 1800
草坪 5 100
行车通道
合计
草坪
10
5
单位:米
情境导入
停车场(A区)
行车通道
2
3
5
15
停车场(B区)
4
复习回顾
∟
平行四边形的面积 =底 高
三角形的面积 =底 高 2
合作探索
1. 先独立思考,能把梯形转化成学过的什么图形。
2.想一想梯形和转化后的图形有什么关系。
3.把你的方法与小组成员交流,试着推导出梯形的面积计算公式。
活动要求:
把两个完全相同的梯形拼成一个平行四边形。
梯形的面积
平行四边形的面积
=
底
×
高
(上底+下底)
×
=
高
÷
2
下底
上底
高
下底
上底
合作探索
÷
2
2
÷
=
上底
把一个梯形割补成一个平行四边形。
合作探索
梯形的面积=(上底+下底)
高÷2
中点
中点
下底
刘徽,三国时期魏国数学家,被称为“中国古代的数学泰斗”,
他最早利用出入相补的原理来计
算平面图形的面积。
数学文化
刘徽,三国时期魏国数学家,被称为“中国古代的数学泰斗”,
他最早利用出入相补的原理来计
算平面图形的面积。
梯形的面积 =(上底 +下底) 高 2
梯形的面积 =(上底 +下底) 高 2
= 两个三角形的面积之和
= 上底 高2+下底高2
梯形的面积
把一个梯形分割成两个三角形。
1
2
=(上底 +下底) 高 2
合作探索
梯形的面积 =(上底 +下底) 高 2
梯形的面积 =(上底 +下底) 高 2
1
2
梯形的面积 = 上底 高2+下底高2
=(上底 +下底) 高 2
b
h
a
梯形的面积 =(上底 +下底) 高 2
S=(a+b) h 2
这些推导过程有什么相同和不同之处?
具体施工要求:
1.停车场(A区)(B区)铺设水泥地面,每平方造价是30元,
2.草坪采用人工铺设草皮,每平方米造价20元。
3.行车通道铺设沥青路面,每平方米造价是80元
停车场施工预算表
停车施工预算表
停车场各部分尺寸及施工要求:
项目 占地面积(平方米) 费用(元)
停车场(A区) 50 1500
停车场(B区) 60 1800
草坪 5 100
行车通道
合计
草坪
10
5
单位:米
基础练习
停车场(A区)
行车通道
2
3
5
15
停车场(B区)
4
37.5
3000
8cm
12cm
100
基础练习
已知梯形的上底是8厘米,下底是12厘米,
面积是100平方厘米,梯形的高是多少厘米?
(1002)(8+12)
=20020
=10(cm)
答:梯形的高是10厘米。
(3+7)×5÷2
= 10 ×5÷2
=25(根)
答:这堆木材共有25根
木材场常常把木材堆成下图形状。算出图中木材的根数,并用梯形的面积公式解释算法。
拓展应用
总根数 =(顶层根数+底层根数)层数 2
3 根
7 根
5 层
7 根
3 根
自主探索 观察下面的图形你有什么发现?
10cm
6cm
10cm
6cm
2cm
10cm
6cm
5cm
10cm
6cm
梯形的面积=(上底+下底)×高÷2
平行四边形的面积=底×高
三角形的面积=底×高÷2
上底=下底
上底=0
转化
总结提升
梯形的面积=(上底+下底) 高 2
......
1.基础性作业:课本自主练习2、5题;
2.实践性作业:你能设计
课后作业
1.基础性作业:课本自主练习2、5题。
2.实践性作业:寻找生活中形状是梯形的物体,测量出它的相关数据,并计算出它的面积。
