垂直于弦的直径及其推论
图片预览

文档简介
课件14张PPT。垂直于弦的直径及其推论山东省嘉祥县第四中学 曾庆坤 13153723886从特殊到一般想一想:将一个圆沿着任一条直径对折,两侧半圆会有什么关系?
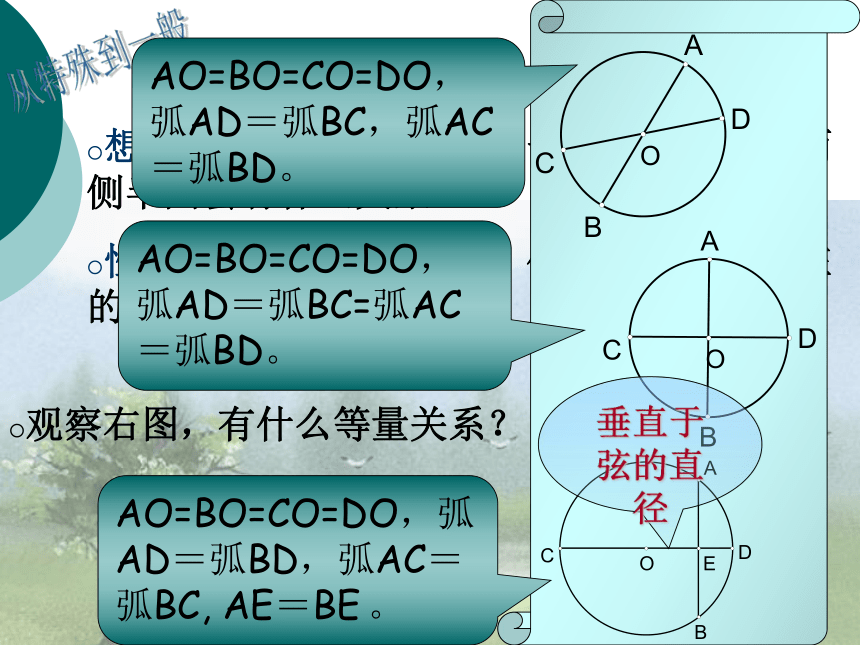
性质:圆是轴对称图形,任何一条直径所在的直线都是它的对称轴。观察右图,有什么等量关系?垂直于弦的直径AO=BO=CO=DO,弧AD=弧BC,弧AC=弧BD。AO=BO=CO=DO,弧AD=弧BC=弧AC=弧BD。AO=BO=CO=DO,弧AD=弧BD,弧AC=弧BC, AE=BE 。证明猜想已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。
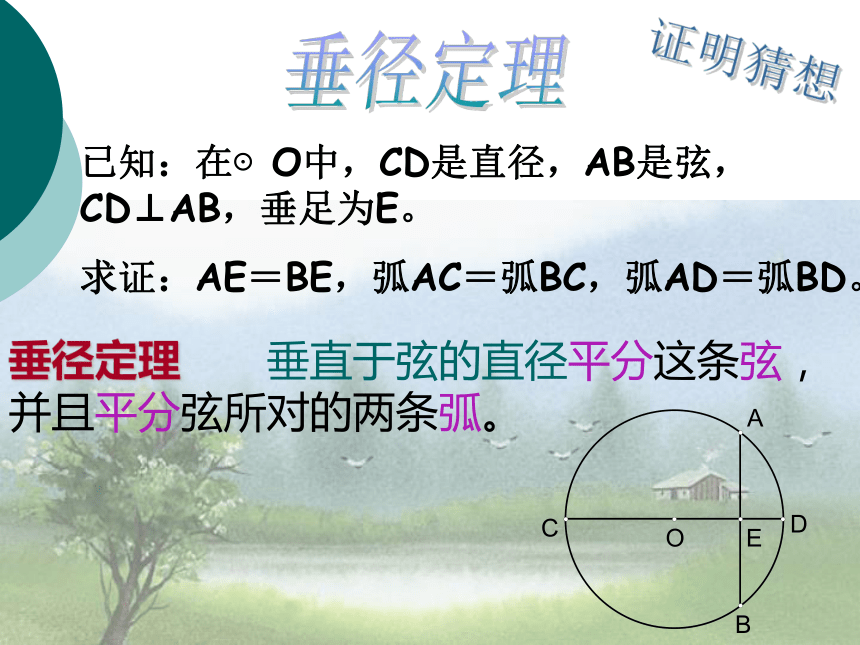
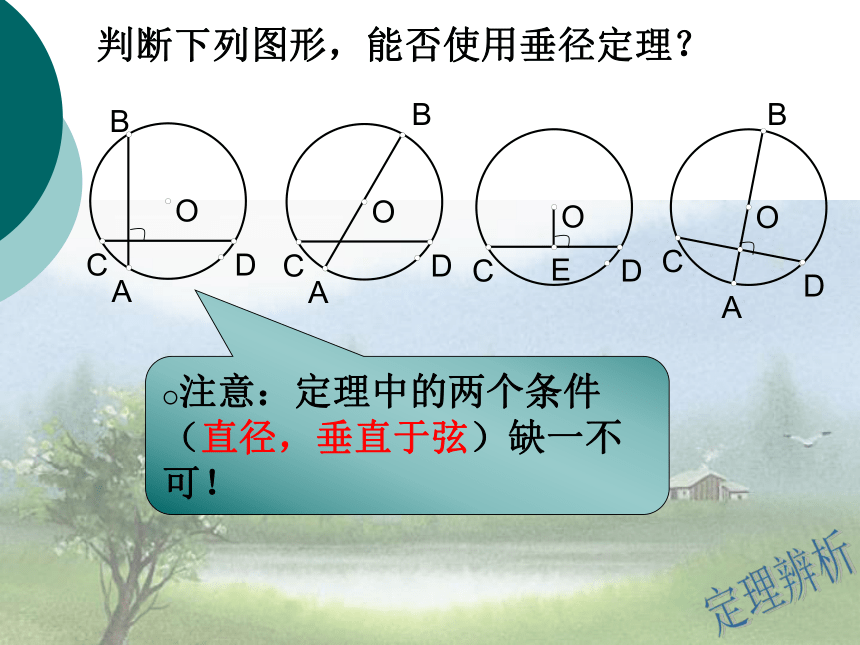
求证:AE=BE,弧AC=弧BC,弧AD=弧BD。垂径定理垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。判断下列图形,能否使用垂径定理?注意:定理中的两个条件(直径,垂直于弦)缺一不可!定理辨析练习例1、已知:在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求: ⊙O的半径。若OA=10cm,OE=6cm,求弦AB的长。
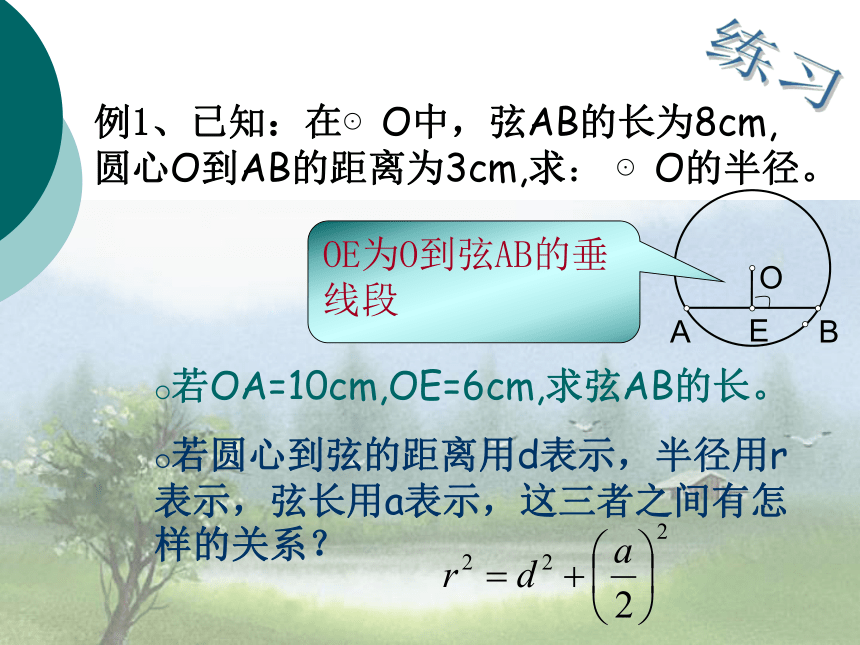
若圆心到弦的距离用d表示,半径用r表示,弦长用a表示,这三者之间有怎样的关系?OE为O到弦AB的垂线段
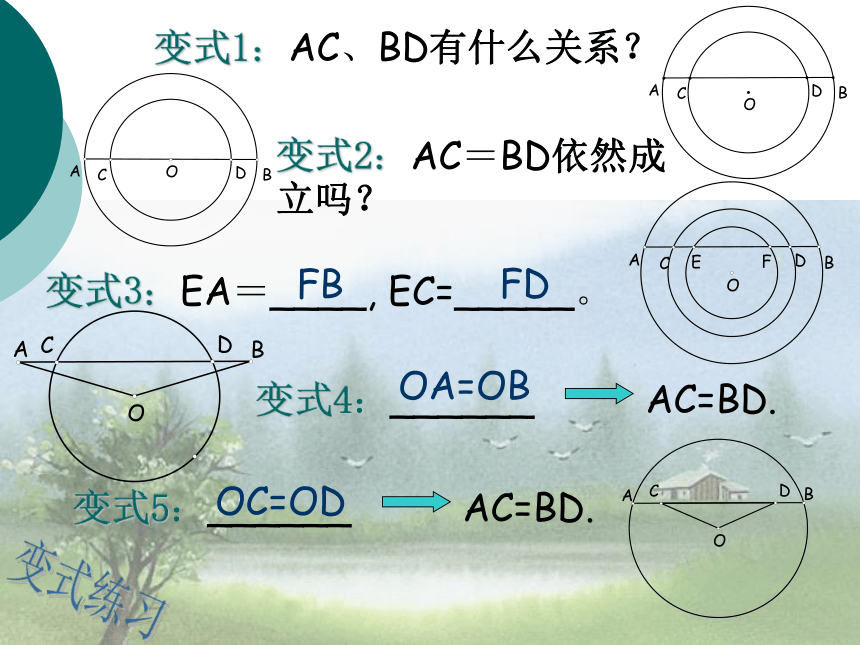
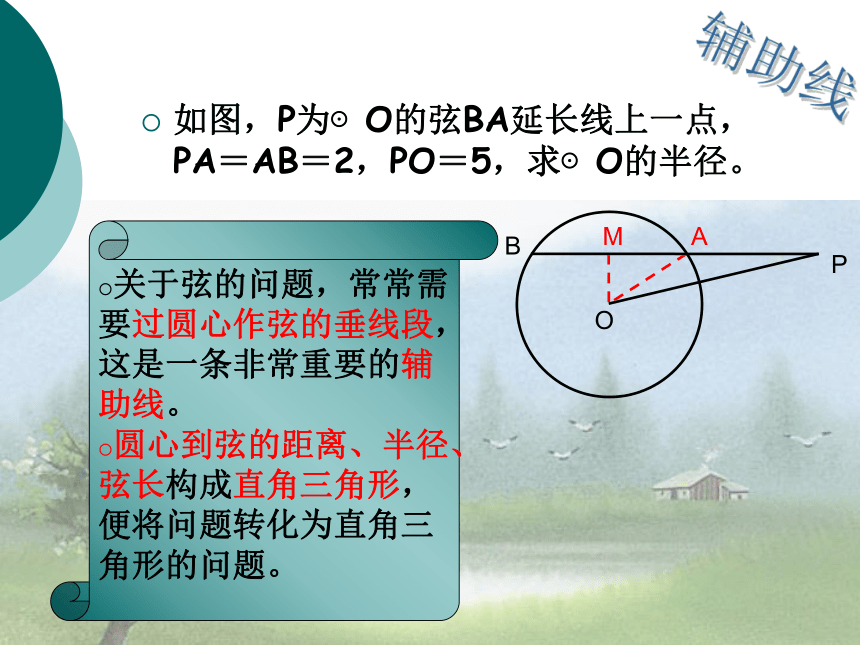
变式1:AC、BD有什么关系?变式2:AC=BD依然成立吗?变式3:EA=____, EC=_____。OA=OBOC=OD变式练习如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径。辅助线关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线。
圆心到弦的距离、半径、弦长构成直角三角形,便将问题转化为直角三角形的问题。综合运用练习已知等腰△ABC的底边BC的长为10cm,顶角为60°,求它的外接圆的直径。
如图,⊙O中CD是弦,AB是直径,AE⊥CD于E,BF⊥CD于F,求证:CE=DF。温故而知新画图叙述垂径定理,并说出定理的题设和结论。想一想:如果将题设和结论中的5个条件适当互换,情况会怎样? (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧。推论1如图,CD为⊙O的直径,AB⊥CD,EF⊥CD,你能得到什么结论?推论2弧AE=弧BF圆的两条平行弦所夹的弧相等。1、填空:如图,在⊙O中
(1)若MN⊥AB,MN为直径;则
( ),( ),( );
(2)若AC=BC,MN为直径;AB不是直径,则
( ),( ),( );
(3)若MN⊥AB,AC=BC,则
( ),( ),( );
(4)若弧AM=弧BM,MN为直径,则
( ),( ),( )。练习练习2、平分已知弧。
3、四等分已知弧。4、已知: ⊙O的半径为6厘米,弦AB与半径OA的夹角为30°。
求:弦AB的长。6、在直径为650毫米的圆柱形油槽内装入一些油后,截面如图所示。若油面宽AB=600毫米,求油的最大深度。5、1300多年前,我国隋代建造的赵州石拱桥的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离,也叫弓形高)为7.2米,求桥拱的半径。(精确到0.1米)。实际问题
性质:圆是轴对称图形,任何一条直径所在的直线都是它的对称轴。观察右图,有什么等量关系?垂直于弦的直径AO=BO=CO=DO,弧AD=弧BC,弧AC=弧BD。AO=BO=CO=DO,弧AD=弧BC=弧AC=弧BD。AO=BO=CO=DO,弧AD=弧BD,弧AC=弧BC, AE=BE 。证明猜想已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。
求证:AE=BE,弧AC=弧BC,弧AD=弧BD。垂径定理垂径定理 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。判断下列图形,能否使用垂径定理?注意:定理中的两个条件(直径,垂直于弦)缺一不可!定理辨析练习例1、已知:在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求: ⊙O的半径。若OA=10cm,OE=6cm,求弦AB的长。
若圆心到弦的距离用d表示,半径用r表示,弦长用a表示,这三者之间有怎样的关系?OE为O到弦AB的垂线段
变式1:AC、BD有什么关系?变式2:AC=BD依然成立吗?变式3:EA=____, EC=_____。OA=OBOC=OD变式练习如图,P为⊙O的弦BA延长线上一点,PA=AB=2,PO=5,求⊙O的半径。辅助线关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线。
圆心到弦的距离、半径、弦长构成直角三角形,便将问题转化为直角三角形的问题。综合运用练习已知等腰△ABC的底边BC的长为10cm,顶角为60°,求它的外接圆的直径。
如图,⊙O中CD是弦,AB是直径,AE⊥CD于E,BF⊥CD于F,求证:CE=DF。温故而知新画图叙述垂径定理,并说出定理的题设和结论。想一想:如果将题设和结论中的5个条件适当互换,情况会怎样? (1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径,垂直平分弦并且平分弦所对的另一条弧。推论1如图,CD为⊙O的直径,AB⊥CD,EF⊥CD,你能得到什么结论?推论2弧AE=弧BF圆的两条平行弦所夹的弧相等。1、填空:如图,在⊙O中
(1)若MN⊥AB,MN为直径;则
( ),( ),( );
(2)若AC=BC,MN为直径;AB不是直径,则
( ),( ),( );
(3)若MN⊥AB,AC=BC,则
( ),( ),( );
(4)若弧AM=弧BM,MN为直径,则
( ),( ),( )。练习练习2、平分已知弧。
3、四等分已知弧。4、已知: ⊙O的半径为6厘米,弦AB与半径OA的夹角为30°。
求:弦AB的长。6、在直径为650毫米的圆柱形油槽内装入一些油后,截面如图所示。若油面宽AB=600毫米,求油的最大深度。5、1300多年前,我国隋代建造的赵州石拱桥的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离,也叫弓形高)为7.2米,求桥拱的半径。(精确到0.1米)。实际问题
同课章节目录
