5.3.1平行线的性质课件(26张PPT)
文档属性
| 名称 | 5.3.1平行线的性质课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 664.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-09 00:00:00 | ||
图片预览







文档简介
课件26张PPT。一、教材说明二、教法说明三、学法说明四、教学程序授课内容 这节课的主要内容是平行线的三个性质。这三个性质是本章的重点内容之一,平行线的三个性质很重要,它们不但为三角形内角和定理的证明提供了转化的方法,而且也为今后三角形全等、三角形相似等知识的学习奠定了理论基础。zxxk
教材简析 1、知识目标:使学生了解平行线的性质和判定的区别。掌握平行线的性质,并且会运用它们进行简单推理和计算。
2、智能目标:使学生领会数形结合、转化、对比的数学思想和方法,从而提高学生分析问题和解决问题的能力。
3、思想目标:通过实际问题的深入和解决向学生渗透几何知识来源于实践并反作用于实践及认识事物的规律 是从特殊到一般,再从一般到特殊等辩证唯物主义观点。Z.xxk
教学目标平行线的三个性质的推导及
运用。教学重点、难点和关键重点关键难点平行线的性质公理的得出过程。通过观察电脑演示、度量等方法,让学生自己确认平行 线的性质公理的存在性和正确性。Zx.xk
1、为了培养学生具有获得知识的能力,可采取引导发现法、讨论式、启发探索三结合的教法。
2、采用电脑和投影仪,增大容量和直观性。Zxx.k
教法说明平行线的性质巩固练习二、是真是假一、快速抢答三、猜猜看四、填空五、数学游戏快速抢答是真是假猜猜看填空数学游戏1、两直线平行,同位角 .
2、两直线平行,内错角 .
3、两直线平行,同旁内角 .
4、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=126 ゜ 可以知道 ∠2 是多少度?为什么?
(2)从 ∠1=126゜ 可以知道 ∠3是多少度?为什么?
(3)从 ∠1=126 ゜ 可以知道 ∠4 是多少度?为什么?Zx..xk
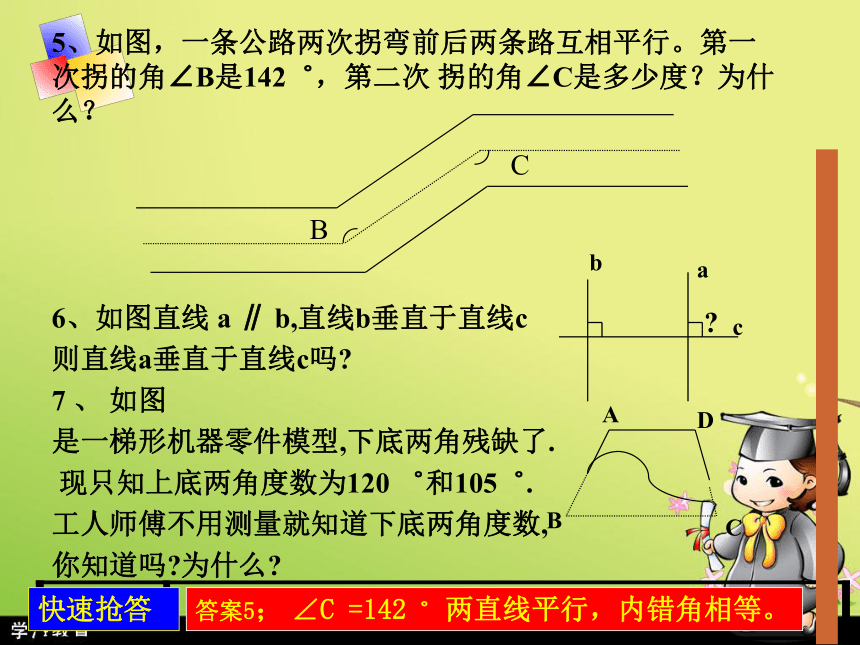
2╭╯1 AEDBC4 (╯3 一、快速抢答快速抢答是真是假猜猜看填空数学游戏(相等)(相等)(互补)5、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
6、如图直线 a ∥ b,直线b垂直于直线c
则直线a垂直于直线c吗?
7 、 如图
是一梯形机器零件模型,下底两角残缺了.
现只知上底两角度数为120 ゜和105゜.
工人师傅不用测量就知道下底两角度数,
你知道吗?为什么?╯ CB╭abc?ADBC快速抢答答案5; ∠C =142゜ 两直线平行,内错角相等。5、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
6、如图直线 a ∥ b,直线b垂直于直线c
则直线a垂直于直线c吗?
7 、 如图
是一梯形机器零件模型,下底两角残缺了.
现只知上底两角度数为115 ゜和100゜.
工人师傅不用测量就知道下底两角度数,
你知道吗?为什么?╯ CB╭abc?ADBC快速抢答答案6 :垂直。5、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
6、如图直线 a ∥ b,直线b垂直于直线c
则直线a垂直于直线c吗?
7 、 如图
是一梯形机器零件模型,下底两角残缺了.
现只知上底两角度数为120゜和105゜.
工人师傅不用测量就知道下底两角度数,
你知道吗?为什么?╯ CB╭abc?ADBC快速抢答答案7:∠B =60゜和75゜ ,两直线平行,同旁内角互补。快速抢答答案8:∠5 =110゜ ∠4 =110゜ ∠3 =110゜8、如图、直线a ∥ b、直线c ∥ d、∠1=110゜ ,
∠5=▁ ゜ ,∠4=▁,∠3=▁。
9、 两条平行线,被第三条直线所截同位角、内错角、
同旁内角各有什么关系 ?你能用一句话概括吗?
╮1 ╮4 ╮2 ╮3abcd5╰ 快速抢答答案9:两条平行线,同位角、内错角和同旁内角都相等。8、如图、直线a ∥ b、直线c ∥ d、∠1=110゜ ,
∠5=▁ ゜ ,∠4=▁,∠3=▁。
9、 两条平行线,被第三条直线所截同位角、内错角、
同旁内角各有什么关系 ?你能用一句话概括吗?
╮1 ╮4 ╮2 ╮3abcd5╰ 1、同位角相等。
2、两直线被第三条直线所截,同位角相等.
3、两直线平行,同旁内角相等。
4、两直线平行,同位角相等,内错角相等,同旁内角互补。
5、内错角相等,两直线平行是性质。
6、两直线平行,内错角相等是判定。
7、如右图 ∵AB ∥CD,∴∠1=∠2 (两直线平行,内错角相等 )
8、 (两直线平行 ,内错角相等 )
9、两直线被第三条直线所截,若同位角相等,
则内错角相等.
10 、如图直线 a∥b,则∠1=∠2
ADBC╮1 2╭ ╮2 abc╮1二、是真是假快速抢答是真是假猜猜看填空数学游戏1、同位角相等。
2、两直线被第三条直线所截,同位角相等.
3、两直线平行,同旁内角相等。
4、两直线平行,同位角相等,内错角相等,同旁内角互补。
5、内错角相等,两直线平行是性质。
6、两直线平行,内错角相等是判定。
7、如右图 ∵AB ∥CD,∴∠1=∠2 (两直线平行,内错角相等 )
8、 (两直线平行 ,内错角相等 )
9、两直线被第三条直线所截,若同位角相等,
则内错角相等.
10 、如图直线 a∥b,则∠1=∠2
ADBC╮1 2╭ ╮2 abc╮1二、是真是假答案:1错2错3错4对5错6错7错8错9对10错1、如果有两条直线被第三条直线所截,那么必定有(A)内错角相等,(B)同位角相等,(C)同旁内角互补,(D)以上都不对。
2、如图
已知∠1= ∠2,要说明 ∠3 +∠4=180゜。
∵∠1= ∠2,∴DE∥ FG (1)
∴∠3 +∠4=180゜ (2)
在 (1)、(2)中依据应是:
(A)(1)两直线平行,同位角相等;
(2) 两直线平行,同旁内角互补。
(B)(1)两直线平行,同位角相等;
(2)同旁内角互补,两直线平行。
(C)(1)同位角相等,两直线平行;
(2)两直线平行,同旁内角互补。
(D)(1)同位角相等,两直线平行;
(2) 同旁内角互补,两直线平行。╮2╮1 ╮4 ╯3 DEFGBCA三、猜 猜 看快速抢答是真是假猜猜看填空数学游戏1、如果有两条直线被第三条直线所截,那么必定有(A)内错角相等,(B)同位角相等,(C)同旁内角互补,(D)以上都不对。
2、如图
已知∠1= ∠2,要说明 ∠3 +∠4=180゜。
∵∠1= ∠2,∴DE∥ FG (1)
∴∠3 +∠4=180゜ (2)
在 (1)、(2)中依据应是:
(A)(1)两直线平行,同位角相等;
(2) 两直线平行,同旁内角互补。
(B)(1)两直线平行,同位角相等;
(2)同旁内角互补,两直线平行。
(C)(1)同位角相等,两直线平行;
(2)两直线平行,同旁内角互补。
(D)(1)同位角相等,两直线平行;
(2) 同旁内角互补,两直线平行。╮2╮1 ╮4 ╯3 DEFGBCA三、猜 猜 看答案:1、D2、C猜猜看 3、两条平行线被第三条直线所截,相等同位角的对数是
( ) A.1 B.2 C.3 D.4
4 、 ∠1 和∠2是两条直线被第三条直线所截形成的同旁内角,要使这两条直线平行,必须( )
A. ∠1= ∠2 B. ∠1+∠2=90 ゜
C. 2(∠1+∠2)=360 ゜ D .∠1是钝角, ∠2是锐角
5 、 如图A D ∥BC,则下面结论中正确的是:
A. ∠1= ∠2 B.∠3= ∠4 C. ∠A
= ∠C D.∠1+ ∠2+ ∠3+ ∠4= 180 ゜
6、在(1)同位角相等(2)两直线平行(3)是判定(4)是性质
中语序排列有(a).(1)(2)(4) (b).(1)(2)(3)
(c).(2)(1)(3) (d).(2)(1)(4),其中语序排列正确的个数有:
A.0个 B. 1个 C.2个 D.3个╮4╮2 DBCA3╰1╰答案:3、D4、C5、B6、C 7、直线a 、b被直线 所截,∠1与 ∠2是同位角。
由∠1= ∠2,得a ∥ b,根据是▁▁
由a ∥ b,得∠1= ∠2,根据是▁▁
8、如图:(选择合适理由添空)
∵AB ∥CD,∴∠B =∠C ( ).
∵ ∠B =∠C , ∴ AB ∥CD( )
(1)两直线平行, 内错角相等 .(2)内错角
相等,两直线平行
9 如图AB ∥CD,则
A. ∠A+∠B=180 ゜ B. ∠B+∠C=180 ゜
C. ∠C+∠D=180 ゜ D. ∠A+∠C=180 ゜
ABCDABDC猜猜看答案:7、同位角相等,两直线平行;两直线平行,同位角相等。7、直线a 、b被直线 所截,∠1与 ∠2是同位角。
由∠1= ∠2,得a ∥ b,根据是▁▁
由a ∥ b,得∠1= ∠2,根据是▁▁
8、如图:(选择合适理由添空)
∵AB ∥CD,∴∠B =∠C ( ).
∵ ∠B =∠C , ∴ AB ∥CD( )
(1)两直线平行, 内错角相等 .(2)内错角
相等,两直线平行
9 如图AB ∥CD,则
A. ∠A+∠B=180 ゜ B. ∠B+∠C=180 ゜
C. ∠C+∠D=180 ゜ D. ∠A+∠C=180 ゜
ABCDABDC猜猜看答案:8、⑴⑵9、D?1、如图:∵∠1= ∠2 (已知)
∴DE∥ BC ( )
∴∠3 =∠4 ( )
2、如图: ∵AB ∥CD (已知)
∴ ∠1= ∠3 ( )
又∠3= ∠2 ( )
∴∠1= ∠2
?又∵ ∠4+ ∠2 =180 ゜( )
∴∠1+ ∠4 =180 ゜ADEBC╮1 ╮2 3╭ 4╭ ABCDEF╮ 1╮3 2╰ 4╭ 四、填 空快速抢答是真是假猜猜看填空数学游戏?1、如图:∵∠1= ∠2 (已知)
∴DE∥ BC ( )
∴∠3 =∠4 ( )
2、如图: ∵AB ∥CD (已知)
∴ ∠1= ∠3 ( )
又∠3= ∠2 ( )
∴∠1= ∠2 ( )
?又∵ ∠4+ ∠2 =180 ゜( )
∴∠1+ ∠4 =180 ゜ADEBC╮1 ╮2 3╭ 4╭ ABCDEF╮ 1╮3 2╰ 4╭ 同位角相等,两直线平行两直线平行,同位角相等两直线平行,同位角相等对顶角相等等量代换邻补角的定义填空答案:( EF;AB;)填空 3、如图:A
∵AB ∥ DF (已知)
∴∠2+ ∠AED=180゜( )
∵AC∥DE (已知)
∴∠C= ∠1 ( )
∵EF ∥ BC (已知)
∴∠4= ∠B ( )
4、如上题图:
∵ ∠1= ∠FED (已知)∴ ____∥BD( )
∵ ∠2= ∠BED (已知)∴ ____∥FD( )ABCFED1╭ ╮3 2⌒5、两条平行线被第三条直线所截,同旁内角的比 3:5, 则这对角分别( )╮4 答案(B;44 ;50;180;DAB;EAC;86;44;50;86;C)填空6、已知直线DE经过点A , DE∥BC ,∠B=44゜ , ∠C=50 ゜
∵DE ∥BC (已知)
∴∠DAB= ∠ _____ = _____ ゜
( )
∵ DE ∥BC (已知)
∴∠EAC= ∠____ = _____ ゜
∠BAC= ____ --- ∠ _____---_ ∠ ______ = ____ ゜
∴∠BAC+ ∠DAB+ ∠CAE = ___+___ + ___ = _____ ゜
7、已知:如图AB ∥CD, ∠A= ∠C要说明AD ∥BC.
法一: 因为AB ∥CD( )
所以∠B+ ∠____ = 180 ゜ ( )
因为∠A= ∠C( )
所以∠B+ ∠A= _____゜( )
所以___ ∥___( )DAEBCDABC
(接上页) 已知:如图AB ∥CD, ∠A= ∠C要说明AD ∥BC.
法二:如图,连结AC,
因为AB ∥CD( )
所以∠1= ∠____ ( )
又因为∠DAB= ∠BCD( )
所以∠DAB-∠2= ∠BCD-∠1
即∠DAC= ∠BCA
所以___ ∥___( )
法三:如图,延长AB至E,
因为AB ∥CD( )
所以∠C= ∠CBE ( )
又因为∠A= ∠C( )
所以∠__= ∠___ ( )
所以AD ∥BC( )DABCABCD╮2 1╰ E答案:(2;AD;BC;A;CBE)填空 如图。这是一付“角棋”。“棋盘”是一些平行线,“棋子”是用彩纸做成的两个角( ∠ 1和∠ 2颜色可不同)下面请两位同学上来,从两头开始“跳”角,执:“∠ 1”、“∠ 2”的双方以跳到对方初始位置为胜,双方轮流进行,每“跳”
一步要说出“跳” 的根据(即平行线的性质),看看谁“跳”得快,理由说得准确。 ╮12╰五、数学游戏快速抢答是真是假猜猜看填空数学游戏
教材简析 1、知识目标:使学生了解平行线的性质和判定的区别。掌握平行线的性质,并且会运用它们进行简单推理和计算。
2、智能目标:使学生领会数形结合、转化、对比的数学思想和方法,从而提高学生分析问题和解决问题的能力。
3、思想目标:通过实际问题的深入和解决向学生渗透几何知识来源于实践并反作用于实践及认识事物的规律 是从特殊到一般,再从一般到特殊等辩证唯物主义观点。Z.xxk
教学目标平行线的三个性质的推导及
运用。教学重点、难点和关键重点关键难点平行线的性质公理的得出过程。通过观察电脑演示、度量等方法,让学生自己确认平行 线的性质公理的存在性和正确性。Zx.xk
1、为了培养学生具有获得知识的能力,可采取引导发现法、讨论式、启发探索三结合的教法。
2、采用电脑和投影仪,增大容量和直观性。Zxx.k
教法说明平行线的性质巩固练习二、是真是假一、快速抢答三、猜猜看四、填空五、数学游戏快速抢答是真是假猜猜看填空数学游戏1、两直线平行,同位角 .
2、两直线平行,内错角 .
3、两直线平行,同旁内角 .
4、如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=126 ゜ 可以知道 ∠2 是多少度?为什么?
(2)从 ∠1=126゜ 可以知道 ∠3是多少度?为什么?
(3)从 ∠1=126 ゜ 可以知道 ∠4 是多少度?为什么?Zx..xk
2╭╯1 AEDBC4 (╯3 一、快速抢答快速抢答是真是假猜猜看填空数学游戏(相等)(相等)(互补)5、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
6、如图直线 a ∥ b,直线b垂直于直线c
则直线a垂直于直线c吗?
7 、 如图
是一梯形机器零件模型,下底两角残缺了.
现只知上底两角度数为120 ゜和105゜.
工人师傅不用测量就知道下底两角度数,
你知道吗?为什么?╯ CB╭abc?ADBC快速抢答答案5; ∠C =142゜ 两直线平行,内错角相等。5、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
6、如图直线 a ∥ b,直线b垂直于直线c
则直线a垂直于直线c吗?
7 、 如图
是一梯形机器零件模型,下底两角残缺了.
现只知上底两角度数为115 ゜和100゜.
工人师傅不用测量就知道下底两角度数,
你知道吗?为什么?╯ CB╭abc?ADBC快速抢答答案6 :垂直。5、如图,一条公路两次拐弯前后两条路互相平行。第一次拐的角∠B是142゜,第二次 拐的角∠C是多少度?为什么?
6、如图直线 a ∥ b,直线b垂直于直线c
则直线a垂直于直线c吗?
7 、 如图
是一梯形机器零件模型,下底两角残缺了.
现只知上底两角度数为120゜和105゜.
工人师傅不用测量就知道下底两角度数,
你知道吗?为什么?╯ CB╭abc?ADBC快速抢答答案7:∠B =60゜和75゜ ,两直线平行,同旁内角互补。快速抢答答案8:∠5 =110゜ ∠4 =110゜ ∠3 =110゜8、如图、直线a ∥ b、直线c ∥ d、∠1=110゜ ,
∠5=▁ ゜ ,∠4=▁,∠3=▁。
9、 两条平行线,被第三条直线所截同位角、内错角、
同旁内角各有什么关系 ?你能用一句话概括吗?
╮1 ╮4 ╮2 ╮3abcd5╰ 快速抢答答案9:两条平行线,同位角、内错角和同旁内角都相等。8、如图、直线a ∥ b、直线c ∥ d、∠1=110゜ ,
∠5=▁ ゜ ,∠4=▁,∠3=▁。
9、 两条平行线,被第三条直线所截同位角、内错角、
同旁内角各有什么关系 ?你能用一句话概括吗?
╮1 ╮4 ╮2 ╮3abcd5╰ 1、同位角相等。
2、两直线被第三条直线所截,同位角相等.
3、两直线平行,同旁内角相等。
4、两直线平行,同位角相等,内错角相等,同旁内角互补。
5、内错角相等,两直线平行是性质。
6、两直线平行,内错角相等是判定。
7、如右图 ∵AB ∥CD,∴∠1=∠2 (两直线平行,内错角相等 )
8、 (两直线平行 ,内错角相等 )
9、两直线被第三条直线所截,若同位角相等,
则内错角相等.
10 、如图直线 a∥b,则∠1=∠2
ADBC╮1 2╭ ╮2 abc╮1二、是真是假快速抢答是真是假猜猜看填空数学游戏1、同位角相等。
2、两直线被第三条直线所截,同位角相等.
3、两直线平行,同旁内角相等。
4、两直线平行,同位角相等,内错角相等,同旁内角互补。
5、内错角相等,两直线平行是性质。
6、两直线平行,内错角相等是判定。
7、如右图 ∵AB ∥CD,∴∠1=∠2 (两直线平行,内错角相等 )
8、 (两直线平行 ,内错角相等 )
9、两直线被第三条直线所截,若同位角相等,
则内错角相等.
10 、如图直线 a∥b,则∠1=∠2
ADBC╮1 2╭ ╮2 abc╮1二、是真是假答案:1错2错3错4对5错6错7错8错9对10错1、如果有两条直线被第三条直线所截,那么必定有(A)内错角相等,(B)同位角相等,(C)同旁内角互补,(D)以上都不对。
2、如图
已知∠1= ∠2,要说明 ∠3 +∠4=180゜。
∵∠1= ∠2,∴DE∥ FG (1)
∴∠3 +∠4=180゜ (2)
在 (1)、(2)中依据应是:
(A)(1)两直线平行,同位角相等;
(2) 两直线平行,同旁内角互补。
(B)(1)两直线平行,同位角相等;
(2)同旁内角互补,两直线平行。
(C)(1)同位角相等,两直线平行;
(2)两直线平行,同旁内角互补。
(D)(1)同位角相等,两直线平行;
(2) 同旁内角互补,两直线平行。╮2╮1 ╮4 ╯3 DEFGBCA三、猜 猜 看快速抢答是真是假猜猜看填空数学游戏1、如果有两条直线被第三条直线所截,那么必定有(A)内错角相等,(B)同位角相等,(C)同旁内角互补,(D)以上都不对。
2、如图
已知∠1= ∠2,要说明 ∠3 +∠4=180゜。
∵∠1= ∠2,∴DE∥ FG (1)
∴∠3 +∠4=180゜ (2)
在 (1)、(2)中依据应是:
(A)(1)两直线平行,同位角相等;
(2) 两直线平行,同旁内角互补。
(B)(1)两直线平行,同位角相等;
(2)同旁内角互补,两直线平行。
(C)(1)同位角相等,两直线平行;
(2)两直线平行,同旁内角互补。
(D)(1)同位角相等,两直线平行;
(2) 同旁内角互补,两直线平行。╮2╮1 ╮4 ╯3 DEFGBCA三、猜 猜 看答案:1、D2、C猜猜看 3、两条平行线被第三条直线所截,相等同位角的对数是
( ) A.1 B.2 C.3 D.4
4 、 ∠1 和∠2是两条直线被第三条直线所截形成的同旁内角,要使这两条直线平行,必须( )
A. ∠1= ∠2 B. ∠1+∠2=90 ゜
C. 2(∠1+∠2)=360 ゜ D .∠1是钝角, ∠2是锐角
5 、 如图A D ∥BC,则下面结论中正确的是:
A. ∠1= ∠2 B.∠3= ∠4 C. ∠A
= ∠C D.∠1+ ∠2+ ∠3+ ∠4= 180 ゜
6、在(1)同位角相等(2)两直线平行(3)是判定(4)是性质
中语序排列有(a).(1)(2)(4) (b).(1)(2)(3)
(c).(2)(1)(3) (d).(2)(1)(4),其中语序排列正确的个数有:
A.0个 B. 1个 C.2个 D.3个╮4╮2 DBCA3╰1╰答案:3、D4、C5、B6、C 7、直线a 、b被直线 所截,∠1与 ∠2是同位角。
由∠1= ∠2,得a ∥ b,根据是▁▁
由a ∥ b,得∠1= ∠2,根据是▁▁
8、如图:(选择合适理由添空)
∵AB ∥CD,∴∠B =∠C ( ).
∵ ∠B =∠C , ∴ AB ∥CD( )
(1)两直线平行, 内错角相等 .(2)内错角
相等,两直线平行
9 如图AB ∥CD,则
A. ∠A+∠B=180 ゜ B. ∠B+∠C=180 ゜
C. ∠C+∠D=180 ゜ D. ∠A+∠C=180 ゜
ABCDABDC猜猜看答案:7、同位角相等,两直线平行;两直线平行,同位角相等。7、直线a 、b被直线 所截,∠1与 ∠2是同位角。
由∠1= ∠2,得a ∥ b,根据是▁▁
由a ∥ b,得∠1= ∠2,根据是▁▁
8、如图:(选择合适理由添空)
∵AB ∥CD,∴∠B =∠C ( ).
∵ ∠B =∠C , ∴ AB ∥CD( )
(1)两直线平行, 内错角相等 .(2)内错角
相等,两直线平行
9 如图AB ∥CD,则
A. ∠A+∠B=180 ゜ B. ∠B+∠C=180 ゜
C. ∠C+∠D=180 ゜ D. ∠A+∠C=180 ゜
ABCDABDC猜猜看答案:8、⑴⑵9、D?1、如图:∵∠1= ∠2 (已知)
∴DE∥ BC ( )
∴∠3 =∠4 ( )
2、如图: ∵AB ∥CD (已知)
∴ ∠1= ∠3 ( )
又∠3= ∠2 ( )
∴∠1= ∠2
?又∵ ∠4+ ∠2 =180 ゜( )
∴∠1+ ∠4 =180 ゜ADEBC╮1 ╮2 3╭ 4╭ ABCDEF╮ 1╮3 2╰ 4╭ 四、填 空快速抢答是真是假猜猜看填空数学游戏?1、如图:∵∠1= ∠2 (已知)
∴DE∥ BC ( )
∴∠3 =∠4 ( )
2、如图: ∵AB ∥CD (已知)
∴ ∠1= ∠3 ( )
又∠3= ∠2 ( )
∴∠1= ∠2 ( )
?又∵ ∠4+ ∠2 =180 ゜( )
∴∠1+ ∠4 =180 ゜ADEBC╮1 ╮2 3╭ 4╭ ABCDEF╮ 1╮3 2╰ 4╭ 同位角相等,两直线平行两直线平行,同位角相等两直线平行,同位角相等对顶角相等等量代换邻补角的定义填空答案:( EF;AB;)填空 3、如图:A
∵AB ∥ DF (已知)
∴∠2+ ∠AED=180゜( )
∵AC∥DE (已知)
∴∠C= ∠1 ( )
∵EF ∥ BC (已知)
∴∠4= ∠B ( )
4、如上题图:
∵ ∠1= ∠FED (已知)∴ ____∥BD( )
∵ ∠2= ∠BED (已知)∴ ____∥FD( )ABCFED1╭ ╮3 2⌒5、两条平行线被第三条直线所截,同旁内角的比 3:5, 则这对角分别( )╮4 答案(B;44 ;50;180;DAB;EAC;86;44;50;86;C)填空6、已知直线DE经过点A , DE∥BC ,∠B=44゜ , ∠C=50 ゜
∵DE ∥BC (已知)
∴∠DAB= ∠ _____ = _____ ゜
( )
∵ DE ∥BC (已知)
∴∠EAC= ∠____ = _____ ゜
∠BAC= ____ --- ∠ _____---_ ∠ ______ = ____ ゜
∴∠BAC+ ∠DAB+ ∠CAE = ___+___ + ___ = _____ ゜
7、已知:如图AB ∥CD, ∠A= ∠C要说明AD ∥BC.
法一: 因为AB ∥CD( )
所以∠B+ ∠____ = 180 ゜ ( )
因为∠A= ∠C( )
所以∠B+ ∠A= _____゜( )
所以___ ∥___( )DAEBCDABC
(接上页) 已知:如图AB ∥CD, ∠A= ∠C要说明AD ∥BC.
法二:如图,连结AC,
因为AB ∥CD( )
所以∠1= ∠____ ( )
又因为∠DAB= ∠BCD( )
所以∠DAB-∠2= ∠BCD-∠1
即∠DAC= ∠BCA
所以___ ∥___( )
法三:如图,延长AB至E,
因为AB ∥CD( )
所以∠C= ∠CBE ( )
又因为∠A= ∠C( )
所以∠__= ∠___ ( )
所以AD ∥BC( )DABCABCD╮2 1╰ E答案:(2;AD;BC;A;CBE)填空 如图。这是一付“角棋”。“棋盘”是一些平行线,“棋子”是用彩纸做成的两个角( ∠ 1和∠ 2颜色可不同)下面请两位同学上来,从两头开始“跳”角,执:“∠ 1”、“∠ 2”的双方以跳到对方初始位置为胜,双方轮流进行,每“跳”
一步要说出“跳” 的根据(即平行线的性质),看看谁“跳”得快,理由说得准确。 ╮12╰五、数学游戏快速抢答是真是假猜猜看填空数学游戏
