平面直角坐标系(1)

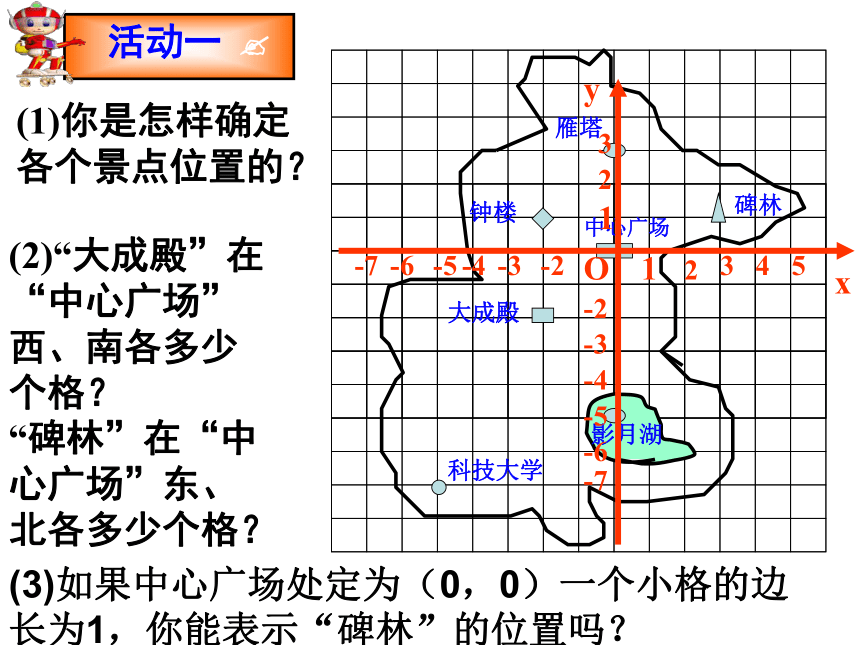
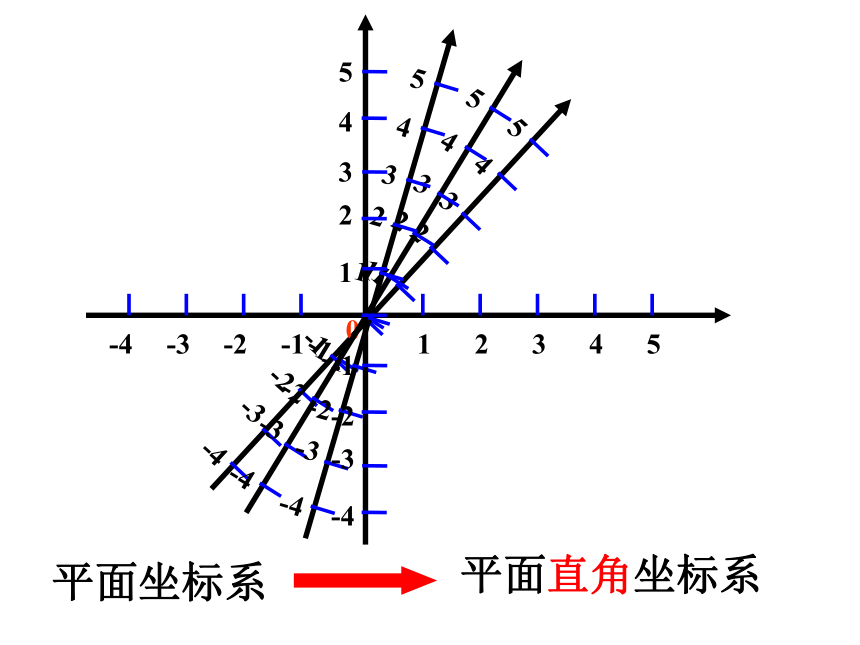
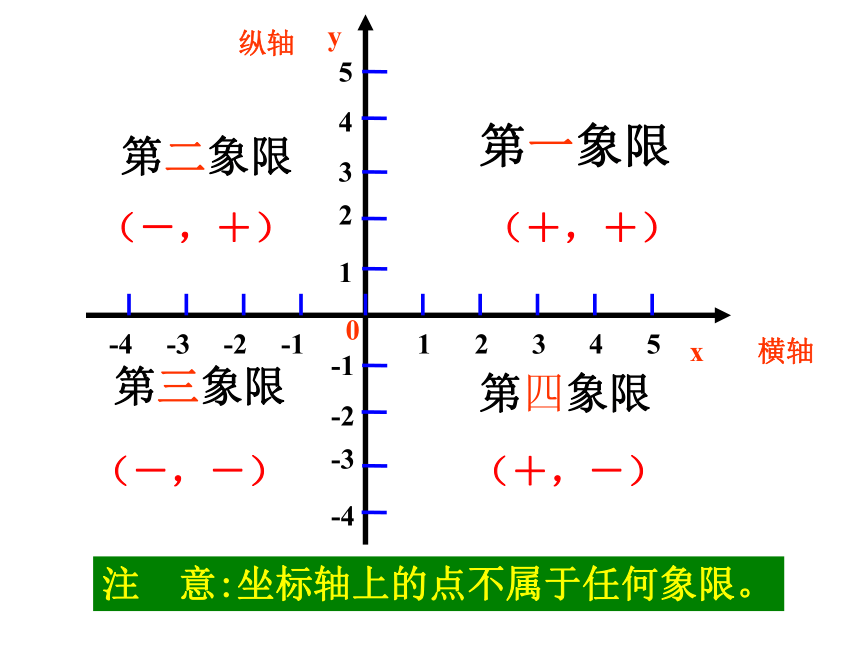
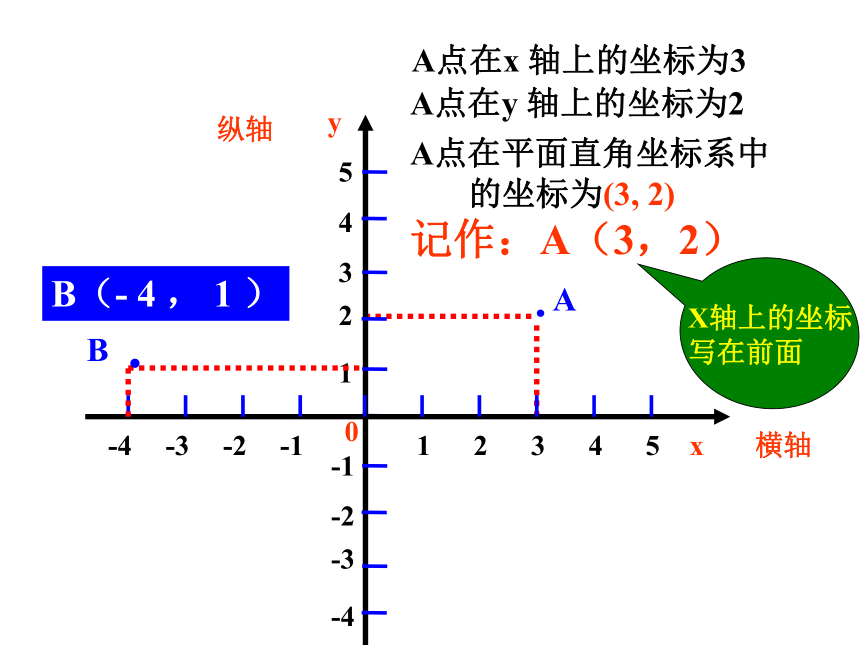
课件18张PPT。5.3平面直角坐标系隆德二中 李伟(1)在平面内，确定物体位置方式有两种：一般记作（a ，b）(横　＋　纵）(方位角＋距离）在平面内，确定物体位置,需两个数据（2）用两种方式确定棋子的位置引入新课 利用“数轴”来确定点的位置（坐标）A数轴上的点 实数（坐标）一一对应(1)你是怎样确定各个景点位置的？(2)“大成殿”在“中心广场”西、南各多少个格？“碑林”在“中心广场”东、北各多少个格？ 活动一 ? (3)如果中心广场处定为（0，0）一个小格的边长为1，你能表示“碑林”的位置吗？平面坐标系平面直角坐标系第一象限第四象限第三象限第二象限注 意:坐标轴上的点不属于任何象限。（＋，＋）（－，＋）（－，－）（＋，－）·AA点在x 轴上的坐标为3A点在y 轴上的坐标为2A点在平面直角坐标系中
的坐标为(3, 2)
记作：A（3，2）B（- 4 ， 1 ）问题1： 如图，坐 标平 面内一点M 的位置已经 确定 ，那么如何来确定点M的坐标 呢 ？关键是： 过点分别作X轴和Y轴的垂线
0-4-3-2-11234X-1-21234 想一想（点N 的坐标又是多少呢？） y ● M 5 6(- 4,3 )(3 ,5) ●N?有 收 获·B·C·A·E·D( 2，3 )( 3，2 )( -2，1 )( -4，- 3 )( 1，- 2 )例1、写出图中A、B、C、D、E各点的坐标。例2、在直角坐标系中，描出下列各点：
A（4，3）、B（-2，3）、C（-4，-1）、
D（2，-2）、E（0，-3） 、F（5，0） .E.F坐标平面上的点P
有序实数对（a,b）一一对应1）点B与C的纵坐标相同，线段BC的位置有什么特点？
2）线段CE的位置有什么特点？
3）坐标轴上点的坐标有什么特点？例3、
写出多边形ABCDEF
各个顶点的坐标。解：A（-2，0）,B（0，-3），C（3，-3），　D（4，0），E（3，3），F（0，3）。（2）点A与D，B与C的纵坐标相同吗？为什么？
A与B，C与D的横坐标相同吗？为什么？ （1）写出图中平行四边形ABCD各个顶点的坐标？A（-3，4）B（-6，-2）C（6，-2）D（9， 4）AD，BC分别平行于横轴，A与D，B与C的纵坐标分别相同；
由于A与B，C与D的连线与横轴斜交，它们向横轴作垂线，垂足不重合，因此，A与B，C与D的横坐标不同。思考：满足下列条件的点P（a，b）
具有什么特征？
（1）当点P分别落在第一象限、第二象限、 第三象限、第四象限时（+，+）（－，+）（－，－）（+，－）xy阶梯训练一思考：满足下列条件的点P（a，b）
具有什么特征？
（2）当点P落在X轴、Y轴上呢？
点P落在原点上呢？xy阶梯训练·（0，b）P（a，0）任何一个在 x轴上的点
的纵坐标都为0。 任何一个在 y轴上的点的横坐标都为0。想一想：下列各点分别在坐标平面的什么位置上？A（3，2）
B（0，－2）
C（－3，－2）
D（－3，0）
E（－1.5，3.5）
F（2，－3）第一象限第三象限第二象限第四象限y轴上x轴上1、纵坐标相同的两点的连线，平行于X轴、垂直于Y轴；规律：2、横坐标相同的两点的连线，平行于Y轴、垂直于X轴；3、坐标轴上的点的坐标至少有一个是0，
横轴上的点的纵 坐标为0，表示为（X，0）
纵轴上的点的横坐标为0，表示为（0，Y） 。1）点B与C的纵坐标相同，线段BC的位置有什么特点？
2）线段CE的位置有什么特点？
3）坐标轴上点的坐标有什么特点？今天你有哪些收获?1.平面直角坐标系的慨念和画法以及点的坐标的表示方式
2.已知点的坐标如何确定点的位置
3. 已知点的位置如何确定点的坐标
4.在平面直角坐标系中画图形，并且初步知道了平面直角坐标系的知识在实际生活中有着广泛应用谈一谈