圆的对称性（1）

课件12张PPT。初三数学备课组3.2圆的对称性（1）垂径定理1 、下列三个银行标志是什么对称图形?2、我们学过哪些轴对称图形？线段、角、等腰三角形、等腰梯形、
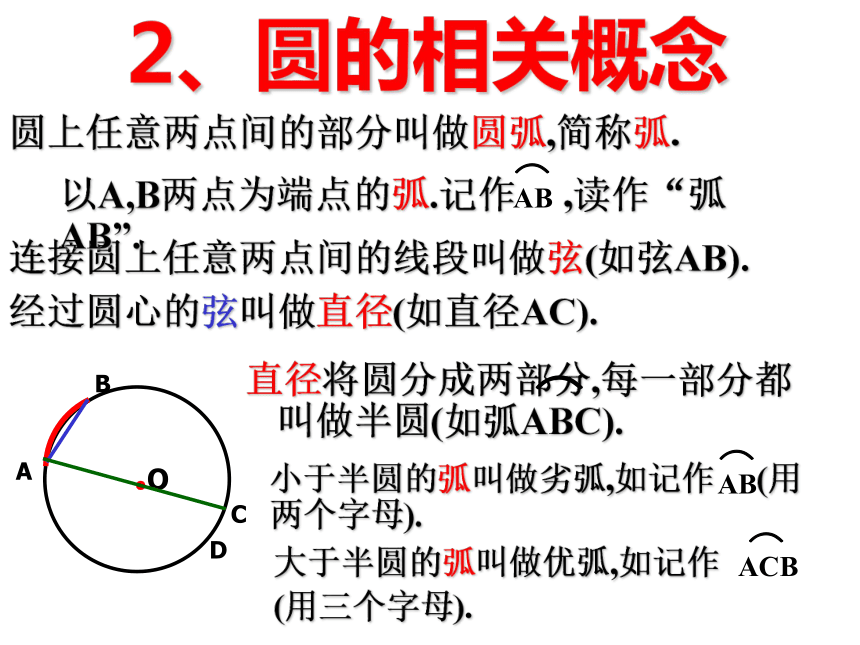
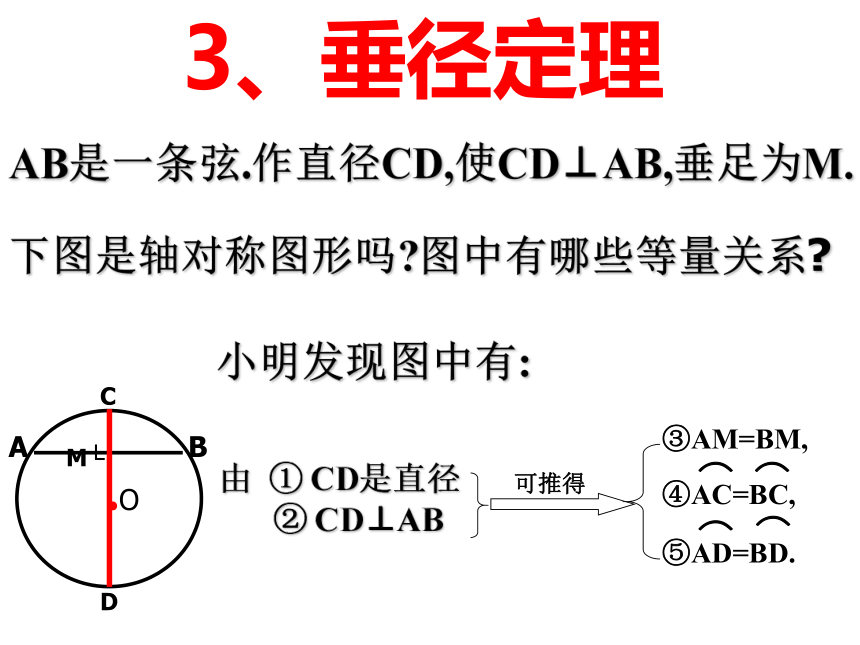
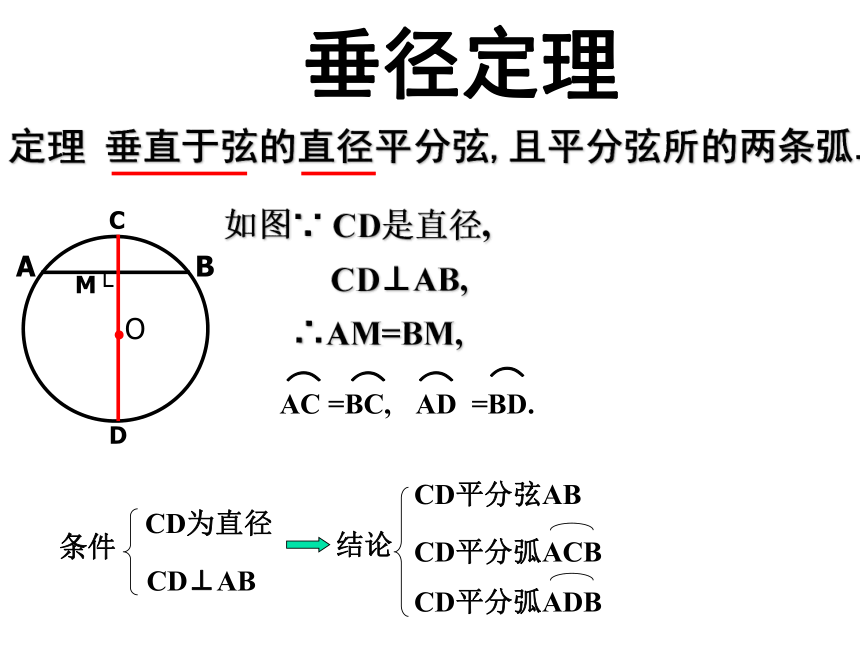
菱形、矩形、正方形轴对称，中心对称轴对称轴对称，中心对称圆是轴对称图形. 圆的对称轴是任意一条经过圆心的直线,它有无数条对称轴.可用折叠的方法解决上述问题.圆也是中心对称图形.它的对称中心就是圆心.用旋转的方法可解决这个问题.1、圆的对称性2、圆的相关概念圆上任意两点间的部分叫做圆弧,简称弧.直径将圆分成两部分,每一部分都叫做半圆(如弧ABC).连接圆上任意两点间的线段叫做弦(如弦AB).经过圆心的弦叫做直径(如直径AC).⌒③AM=BM,3、垂径定理AB是一条弦.作直径CD,使CD⊥AB,垂足为M.下图是轴对称图形吗?图中有哪些等量关系?小明发现图中有: 由 ① CD是直径② CD⊥AB垂径定理定理 垂直于弦的直径平分弦,且平分弦所的两条弧.CD⊥AB,如图∵ CD是直径,∴AM=BM,1、如图在⊙O中，弦AB长为8厘米，O到AB距离为3厘米，⊙O的半径_____。553.在⊙O 中，半径 OC ⊥ AB交AB于D，⊙O 的半径为5cm ，OD =3cm ，弦AB= .2、圆O的弦AB＝8 ㎝ ，DC＝2㎝，
直径CE⊥AB于D，半径OC=____8ACOB 例1：如图，一条公路的转弯处是一段圆弧，（即图中CD，点O是CD的圆心），其中CD =600m，E为CD上一点，且OE⊥CD，垂足为F，EF=90m。求这段弯路的半径。解：连接OC设弯路的半径为R m，则
OF=（R－90）m ∵OE⊥CD
∴CF=1/2×CD=1/2 ×600 = 300（m）
根据勾股定理， OC2 = CF2 + OF2
即 R2=3002 +（R-90）2
解得 R = 545
所以，这段弯路的半径为545m。RR-90300例2 已知：如图，在以O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D两点。
求证：AC＝BD。证明：过O作OE⊥AB，垂足为E，则AE＝BE，CE＝DE。
AE－CE＝BE－DE。
所以，AC＝BDE思考题1（1）在半径为１３的圆Ｏ中，弦ＡＢ＝２4，弦ＡＢ上有一动点Ｐ，则ＯＰ的取值范围是　　　　　　　　　。（2）在半径为１0的圆Ｏ内，有一定点Q，且OQ=6，过点Q的弦AB取值范围是　　 　　。ABPOOQC5≤ＯＰ≤1316≤AB≤20动点CD为圆O的直径，弦AB交CD于E， ∠ CEB=30°，DE=10㎝，CE=2㎝，
求弦AB的长。思考题2FE小结: 解决有关弦的问题，经常是过圆心作弦的垂线，或作垂直于弦的直径，连结半径等辅助线，为应用垂径定理创造条件。