3.圆的对称性(2)
图片预览


文档简介
课件11张PPT。初三数学备课组3.2圆的对称性(2)
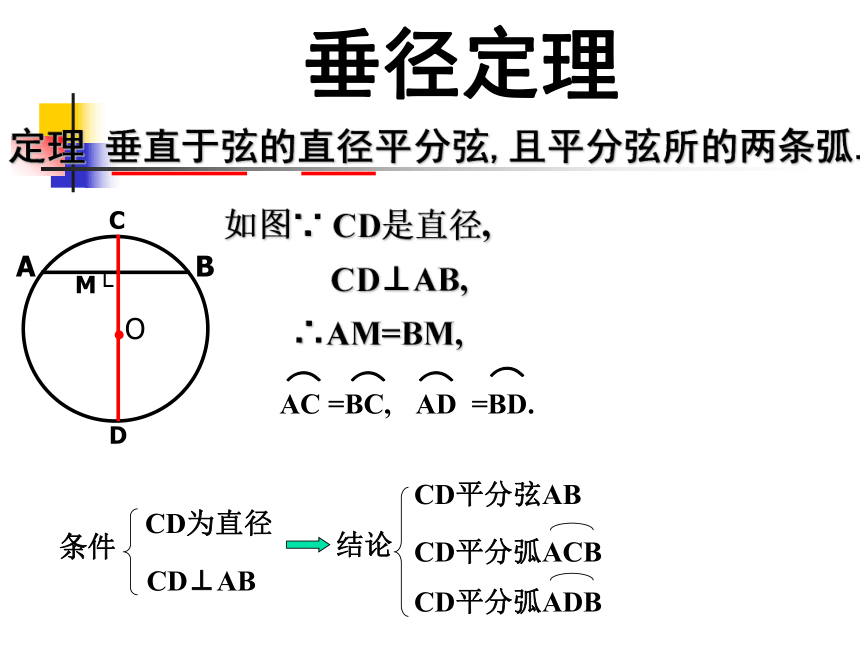
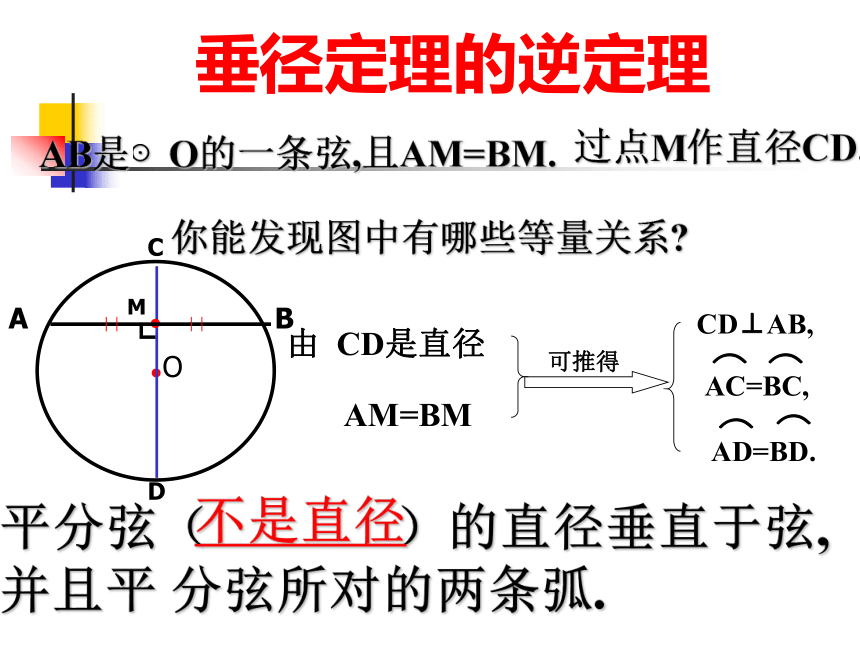
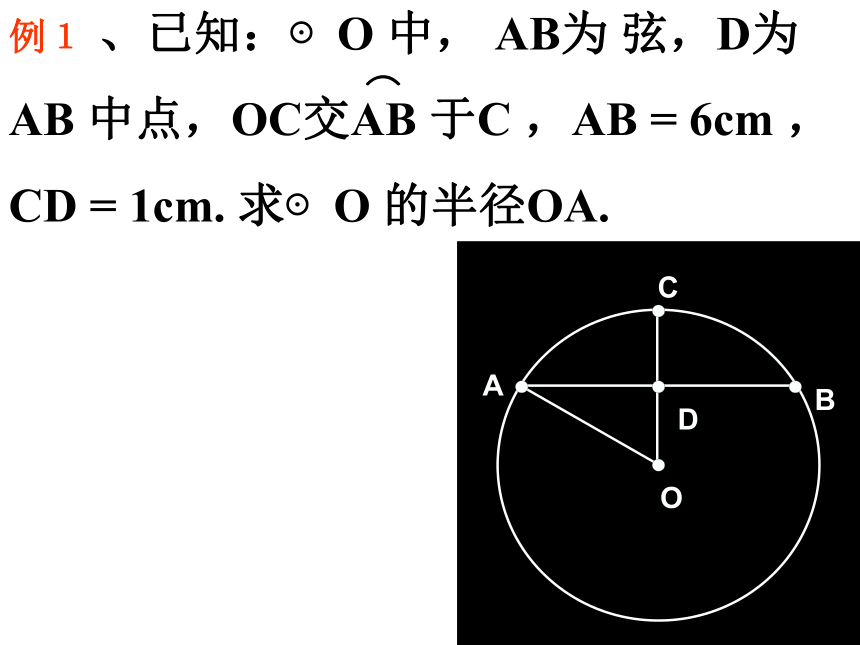
垂径定理的应用垂径定理定理 垂直于弦的直径平分弦,且平分弦所的两条弧.CD⊥AB,如图∵ CD是直径,∴AM=BM,CD⊥AB,垂径定理的逆定理AB是⊙O的一条弦,且AM=BM. 你能发现图中有哪些等量关系?过点M作直径CD. 由 CD是直径 AM=BM┗平分弦( )的直径垂直于弦,并且平 分弦所对的两条弧.M不是直径判断(1)垂直于弦的直线平分弦,并且平分弦所对的弧…………………..( )(3)弦所对的两弧中点的连线,垂直于弦,并且经过圆心………...…..( )(2)平分弦的直径垂直于弦,并且平分弦所对的两条弧………………( )(4)圆内两条非直径的弦不能互相平分( )×√×√例1 、已知:⊙O 中, AB为 弦,D为
AB 中点,OC交AB 于C ,AB = 6cm ,
CD = 1cm. 求⊙O 的半径OA.⌒ 如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?老师提示: 这两条弦在圆中位置有两种情况:垂径定理的推论
圆的两条平行弦所夹的弧相等.EE1、在半径为50㎜的圆O中,有长50㎜的
弦AB,(1)点O与AB的距离为_____
⑵∠AOB的度数为_____6002、在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,油的最大深度 mm200CD5025OABD3、在直径为650mm的圆柱形油槽内装入一些油后,截面如图.若油面宽AB = 600mm,求油的最大深度. DC已知:AB和CD是⊙O内的两条平行弦,,AB=6cm,CD=8cm,⊙O的半径为5cm,(1)根据题意画出符合条件的图形(2)求出AB、与CD间的距离。例2435543EFEF=4+3=7EFEF=4-3=1解得 R≈3.9(m).在Rt△ONH中,由勾股定理∴此货船能顺利通过这座拱桥. 有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗? 解:用 表示桥拱, 圆心为O,半径为Rm,经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C. 据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.则例3 船能过拱桥吗?1、垂径定理平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.2、垂径定理的逆定理 由 CD是直径 AM=BMCD⊥AB,圆的两条平行弦所夹的弧相等.3、垂径定理的推论
垂径定理的应用垂径定理定理 垂直于弦的直径平分弦,且平分弦所的两条弧.CD⊥AB,如图∵ CD是直径,∴AM=BM,CD⊥AB,垂径定理的逆定理AB是⊙O的一条弦,且AM=BM. 你能发现图中有哪些等量关系?过点M作直径CD. 由 CD是直径 AM=BM┗平分弦( )的直径垂直于弦,并且平 分弦所对的两条弧.M不是直径判断(1)垂直于弦的直线平分弦,并且平分弦所对的弧…………………..( )(3)弦所对的两弧中点的连线,垂直于弦,并且经过圆心………...…..( )(2)平分弦的直径垂直于弦,并且平分弦所对的两条弧………………( )(4)圆内两条非直径的弦不能互相平分( )×√×√例1 、已知:⊙O 中, AB为 弦,D为
AB 中点,OC交AB 于C ,AB = 6cm ,
CD = 1cm. 求⊙O 的半径OA.⌒ 如果圆的两条弦互相平行,那么这两条弦所夹的弧相等吗?老师提示: 这两条弦在圆中位置有两种情况:垂径定理的推论
圆的两条平行弦所夹的弧相等.EE1、在半径为50㎜的圆O中,有长50㎜的
弦AB,(1)点O与AB的距离为_____
⑵∠AOB的度数为_____6002、在直径为650mm的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB = 600mm,油的最大深度 mm200CD5025OABD3、在直径为650mm的圆柱形油槽内装入一些油后,截面如图.若油面宽AB = 600mm,求油的最大深度. DC已知:AB和CD是⊙O内的两条平行弦,,AB=6cm,CD=8cm,⊙O的半径为5cm,(1)根据题意画出符合条件的图形(2)求出AB、与CD间的距离。例2435543EFEF=4+3=7EFEF=4-3=1解得 R≈3.9(m).在Rt△ONH中,由勾股定理∴此货船能顺利通过这座拱桥. 有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗? 解:用 表示桥拱, 圆心为O,半径为Rm,经过圆心O作弦AB的垂线OD,D为垂足,与 相交于点C. 据垂径定理,D是AB的中点,C是 的中点,CD就是拱高.则例3 船能过拱桥吗?1、垂径定理平分弦(不是直径)的直径垂直于弦,并且平 分弦所对的两条弧.2、垂径定理的逆定理 由 CD是直径 AM=BMCD⊥AB,圆的两条平行弦所夹的弧相等.3、垂径定理的推论
