四川省成都市龙泉第一中学2015-2016学年高二下学期入学考试数学(文)试题
文档属性
| 名称 | 四川省成都市龙泉第一中学2015-2016学年高二下学期入学考试数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 712.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-09 00:00:00 | ||
图片预览



文档简介
龙泉一中高二年级下学期开学考试
数学(文科)试题
一、选择题(本大题共12小题,每小题5分,共计60分。)
1.若“”, “”,则是的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.命题: “对任意的,”的否定是
A.不存在, B.存在,
C.存在, D.对任意的,
3.如图是某样本数据的茎叶图,则该样本数据的茎叶图,
则该样本数据的中位数
A.22 B.25 C.28 D.31
4.执行如图所示的程序框图,则输出的等于
A.32 B.30
C.20 D. 0
5.已知直线的倾斜角为,若,
则该直线的斜率为
A. B. C. D.
6.已知、是两个平面,、是两条直线,则下列命题不正确的是
A.若,,则 B.若,,则
C.若,,则 D.若,,则
7.已知点,则直线的方程为
A. B.
C. D.
8.如图,一个空间几何体的正视图、侧视图、俯
视图为全等的等腰直角三角形,若直角三角形
的直角边为1,那么这个几何体体积为
A. B. C. D.
9.点关于直线对称的点的坐标是
A. B. C. D.
10.如图,已知正三棱柱的
各条棱长都相等,则异面直线和
所成的角的余弦值大小为
A. B. C. D.
11.已知关于的二次函数,设集合,,分别从集合和中随机取一个数记为和,则函数在上单调递增的概率为
A. B. C. D.
12.在中,,是的角平分线(如图①)。若沿直线将折成直二面角(如图②)。则折叠后两点间的距离为
( http: / / www.21cnjy.com )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共计20分)
13.设直线与间的距离为,则 ▲ 。
14.执行如图所示的程序框图,则输出的等于 ▲ 。
15.已知一圆锥的侧面展开图是半径为2的半圆,则该圆锥的体积为 ▲ 。
16.已知圆,直线与的交点设为点,过点向圆作两条切线分别与圆相切于两点,则 ▲ 。
三、解答题(17至21每小题12分,22题10分共计70分)
17、(本题满分12分)
某企业准备投资1200万元兴办一所中学,对当地教育市场进行调查后,得到了如下的数据表格(以班级为单位):
学段 硬件建设(万元) 配备教师数 教师年薪(万元)
初中 26 / 班 2 / 班 2 / 人
高中 54 / 班 3 / 班 2 / 人
因生源和环境等因素,全校总班级至少20个班,至多30个班。
(Ⅰ)请用数学关系式表示上述的限制条件;(设开设初中班x个,高中班y个)
(Ⅱ)若每开设一个初、高中班,可分别获得年利润2万元、3万元,请你合理规划办学规模使年利润最大,最大为多少?
▲
18.(本题满分12分)
设实数满足,其中;实数满足。
(1)若,且为真,求实数的取值范围;
(2)若是的充分不必要条件,求实数的取值范围。
▲
19.(本题满分12分)
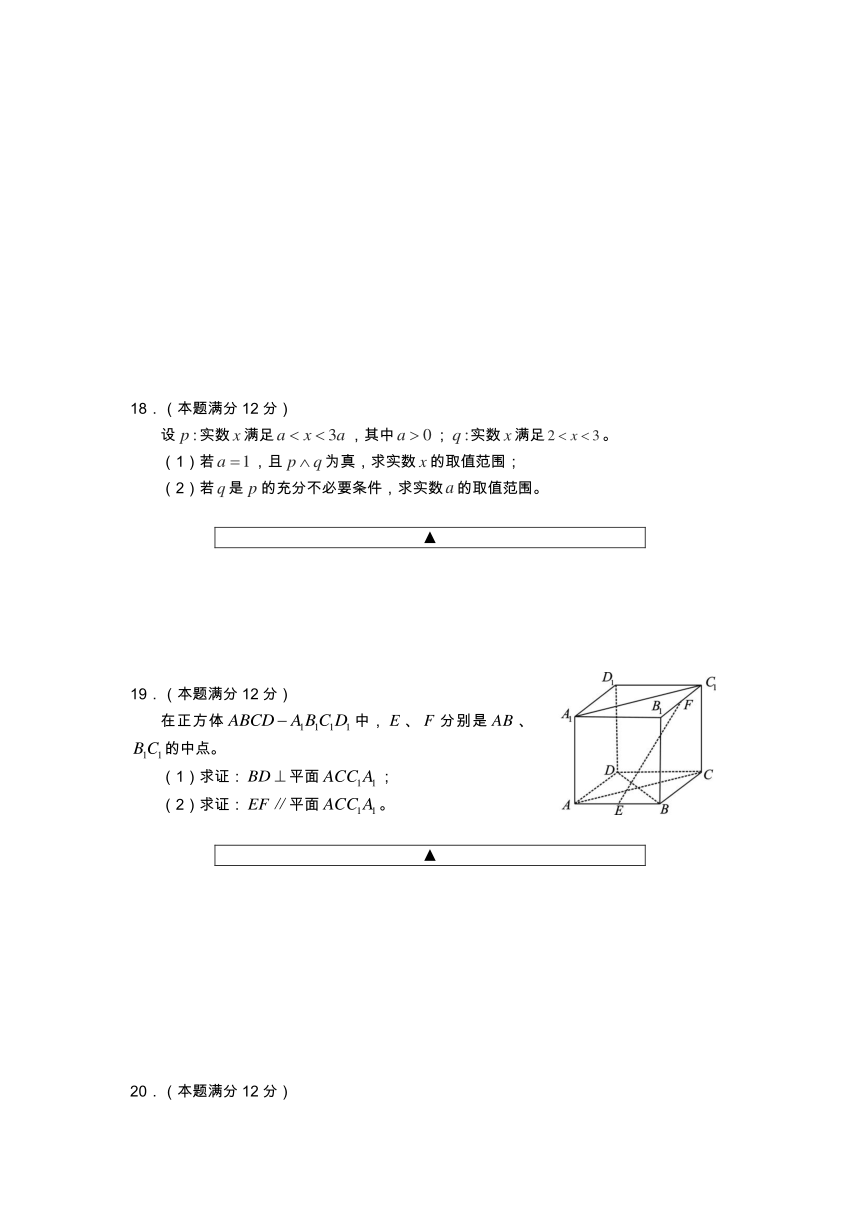
在正方体中,、分别是、的中点。
(1)求证:平面;
(2)求证:平面。
▲
20.(本题满分12分)
某高校在2015年的自主招生考试成绩中随机抽取名学生的笔试
成绩,按成绩分组,得到的频率分布表如下表所示.
组号 分组 频数 频率
第组
第组
第组
第组
第组
合计
(1)求频率分布表中的值,并补充完整相应的频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定 ( http: / / www.21cnjy.com )在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率。
▲
21.(本题满分10分)
已知平面直角坐标系上一动点到点的距离是点到点的距离的倍。
(1)求点的轨迹方程;
(2)过点的直线与点的轨迹相交于两点,点,则是否存在直线,使取得最大值,若存在,求出此时的方程,若不存在,请说明理由。
▲
22.(本题满分12分)
如图,正四棱锥的底面是正方形,每条侧棱的长都是底面边长的倍,,点在侧棱上,且。
(1)求证:;
(2)求三棱锥的体积。
▲
龙泉一中高二年级下学期开学考试
数学(文科)答案
一、选择题(5×12=60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A C B B A D C D C A D B
二、填空题(每小题5分,共20分)
13.2 14.4 15. 16.
三、解答题(共70分)
17.(本题满分12分)
解:(Ⅰ)设开设初中班x个,高中班y个,…………1分
根据题意,线性约束条件为
……5分
即 ……6分
(Ⅱ)设年利润为z万元,则目标函数为 ……7分
由(Ⅰ)作出可行域如图 ……9分
由方程组 得交点M(20,10)
作直线 ,平移,当过点M(20,10),z取最大值70。
∴开设20个初中班,10个高中班时,年利润最大,最大利润为70万元。 ……12分
18.(本题满分12分)
解:(1)当时,若命题为真,则;若命题为真,则,
∵为真,即,都为真,
∴,即实数的取值范围是。…………………………………6分
(2)若是的充分不必要条件,则,
所以,实数的取值范围是。……………………………………………12分
19.(本题满分12分)
解:(1)∵为正方体,
∴,平面,
∵平面,则,
又∵,
∴平面。…………………………6分
(2)设的中点为,连接。
∵E、G分别是、BC的中点,则,
∵,
∴平面,同理平面。
又∵,则平面平面,
∵平面,
∴平面……………12分
20.(本题满分12分)
解:(1)由已知:,
,
∴………………………4分
(注:若未保留至小数点后3位,则扣1分,
图补全2分,即第(1)小题满分6分)
(2)由已知,笔试成绩高的第3、4、5组的
人数之比为3:2:1,现用分层抽样的方法选6名学生。故第3、4、5组每组各抽学生人数为3、2、1。………………………8分
(3)在(2)的前提下,记第3组的3名学生为,
第4组的2名学生为,第5组的1名学生为,且“第4组至少有1名学生被甲考官面试”为事件。
则所有的基本事件有:,,,,,,,,,,,,,,,一共15种。………………………………10分
事件有:,,,,,,,,,一共9种。…………………………………11分
∴
答:第4组至少有1名学生被甲考官面试的概率为。………………12分
21.(本题满分12分)
解:(1)由已知,,………………………2分
∴,即,…………………………………………5分
(2)由题意知的斜率一定存在,不妨假设存直线的斜率为k,且。
则,
联立方程:,………………7分
∴,………………………8分
又∵直线不经过点,则。………………………9分
∵点到直线的距离,,
∴,
∵,
∴当时,取得最大值2,此时,……11分
∴直线的方程为。………………………12分
22.(本题满分10分)
解:(1)设的中点为,连接。
由已知,,底面,
∵平面,
∴,
又∵,
∴平面,
∵平面,
∴。…………………5分
(2)在边上找一点,连接,使。
由已知,底面,
∴底面,……………………6分
又由已知,
则
∵∽,且则,,
∴。…………………………10分
O
Q
数学(文科)试题
一、选择题(本大题共12小题,每小题5分,共计60分。)
1.若“”, “”,则是的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.命题: “对任意的,”的否定是
A.不存在, B.存在,
C.存在, D.对任意的,
3.如图是某样本数据的茎叶图,则该样本数据的茎叶图,
则该样本数据的中位数
A.22 B.25 C.28 D.31
4.执行如图所示的程序框图,则输出的等于
A.32 B.30
C.20 D. 0
5.已知直线的倾斜角为,若,
则该直线的斜率为
A. B. C. D.
6.已知、是两个平面,、是两条直线,则下列命题不正确的是
A.若,,则 B.若,,则
C.若,,则 D.若,,则
7.已知点,则直线的方程为
A. B.
C. D.
8.如图,一个空间几何体的正视图、侧视图、俯
视图为全等的等腰直角三角形,若直角三角形
的直角边为1,那么这个几何体体积为
A. B. C. D.
9.点关于直线对称的点的坐标是
A. B. C. D.
10.如图,已知正三棱柱的
各条棱长都相等,则异面直线和
所成的角的余弦值大小为
A. B. C. D.
11.已知关于的二次函数,设集合,,分别从集合和中随机取一个数记为和,则函数在上单调递增的概率为
A. B. C. D.
12.在中,,是的角平分线(如图①)。若沿直线将折成直二面角(如图②)。则折叠后两点间的距离为
( http: / / www.21cnjy.com )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共计20分)
13.设直线与间的距离为,则 ▲ 。
14.执行如图所示的程序框图,则输出的等于 ▲ 。
15.已知一圆锥的侧面展开图是半径为2的半圆,则该圆锥的体积为 ▲ 。
16.已知圆,直线与的交点设为点,过点向圆作两条切线分别与圆相切于两点,则 ▲ 。
三、解答题(17至21每小题12分,22题10分共计70分)
17、(本题满分12分)
某企业准备投资1200万元兴办一所中学,对当地教育市场进行调查后,得到了如下的数据表格(以班级为单位):
学段 硬件建设(万元) 配备教师数 教师年薪(万元)
初中 26 / 班 2 / 班 2 / 人
高中 54 / 班 3 / 班 2 / 人
因生源和环境等因素,全校总班级至少20个班,至多30个班。
(Ⅰ)请用数学关系式表示上述的限制条件;(设开设初中班x个,高中班y个)
(Ⅱ)若每开设一个初、高中班,可分别获得年利润2万元、3万元,请你合理规划办学规模使年利润最大,最大为多少?
▲
18.(本题满分12分)
设实数满足,其中;实数满足。
(1)若,且为真,求实数的取值范围;
(2)若是的充分不必要条件,求实数的取值范围。
▲
19.(本题满分12分)
在正方体中,、分别是、的中点。
(1)求证:平面;
(2)求证:平面。
▲
20.(本题满分12分)
某高校在2015年的自主招生考试成绩中随机抽取名学生的笔试
成绩,按成绩分组,得到的频率分布表如下表所示.
组号 分组 频数 频率
第组
第组
第组
第组
第组
合计
(1)求频率分布表中的值,并补充完整相应的频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定 ( http: / / www.21cnjy.com )在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率。
▲
21.(本题满分10分)
已知平面直角坐标系上一动点到点的距离是点到点的距离的倍。
(1)求点的轨迹方程;
(2)过点的直线与点的轨迹相交于两点,点,则是否存在直线,使取得最大值,若存在,求出此时的方程,若不存在,请说明理由。
▲
22.(本题满分12分)
如图,正四棱锥的底面是正方形,每条侧棱的长都是底面边长的倍,,点在侧棱上,且。
(1)求证:;
(2)求三棱锥的体积。
▲
龙泉一中高二年级下学期开学考试
数学(文科)答案
一、选择题(5×12=60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 A C B B A D C D C A D B
二、填空题(每小题5分,共20分)
13.2 14.4 15. 16.
三、解答题(共70分)
17.(本题满分12分)
解:(Ⅰ)设开设初中班x个,高中班y个,…………1分
根据题意,线性约束条件为
……5分
即 ……6分
(Ⅱ)设年利润为z万元,则目标函数为 ……7分
由(Ⅰ)作出可行域如图 ……9分
由方程组 得交点M(20,10)
作直线 ,平移,当过点M(20,10),z取最大值70。
∴开设20个初中班,10个高中班时,年利润最大,最大利润为70万元。 ……12分
18.(本题满分12分)
解:(1)当时,若命题为真,则;若命题为真,则,
∵为真,即,都为真,
∴,即实数的取值范围是。…………………………………6分
(2)若是的充分不必要条件,则,
所以,实数的取值范围是。……………………………………………12分
19.(本题满分12分)
解:(1)∵为正方体,
∴,平面,
∵平面,则,
又∵,
∴平面。…………………………6分
(2)设的中点为,连接。
∵E、G分别是、BC的中点,则,
∵,
∴平面,同理平面。
又∵,则平面平面,
∵平面,
∴平面……………12分
20.(本题满分12分)
解:(1)由已知:,
,
∴………………………4分
(注:若未保留至小数点后3位,则扣1分,
图补全2分,即第(1)小题满分6分)
(2)由已知,笔试成绩高的第3、4、5组的
人数之比为3:2:1,现用分层抽样的方法选6名学生。故第3、4、5组每组各抽学生人数为3、2、1。………………………8分
(3)在(2)的前提下,记第3组的3名学生为,
第4组的2名学生为,第5组的1名学生为,且“第4组至少有1名学生被甲考官面试”为事件。
则所有的基本事件有:,,,,,,,,,,,,,,,一共15种。………………………………10分
事件有:,,,,,,,,,一共9种。…………………………………11分
∴
答:第4组至少有1名学生被甲考官面试的概率为。………………12分
21.(本题满分12分)
解:(1)由已知,,………………………2分
∴,即,…………………………………………5分
(2)由题意知的斜率一定存在,不妨假设存直线的斜率为k,且。
则,
联立方程:,………………7分
∴,………………………8分
又∵直线不经过点,则。………………………9分
∵点到直线的距离,,
∴,
∵,
∴当时,取得最大值2,此时,……11分
∴直线的方程为。………………………12分
22.(本题满分10分)
解:(1)设的中点为,连接。
由已知,,底面,
∵平面,
∴,
又∵,
∴平面,
∵平面,
∴。…………………5分
(2)在边上找一点,连接,使。
由已知,底面,
∴底面,……………………6分
又由已知,
则
∵∽,且则,,
∴。…………………………10分
O
Q
同课章节目录
