甘肃省酒泉市第三中学北师大版八年级数学上册课件《7.5 三角形的外角》(共21张PPT)
文档属性
| 名称 | 甘肃省酒泉市第三中学北师大版八年级数学上册课件《7.5 三角形的外角》(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 173.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-09 23:11:13 | ||
图片预览





文档简介
课件21张PPT。7.5 三角形的外角1.直角三角形的两锐角之和是多少度?等边三角形的一个内角是多少度?请证明你的结论.已知:如图在△ABC中,DE∥BC,∠A=600, ∠C=700.
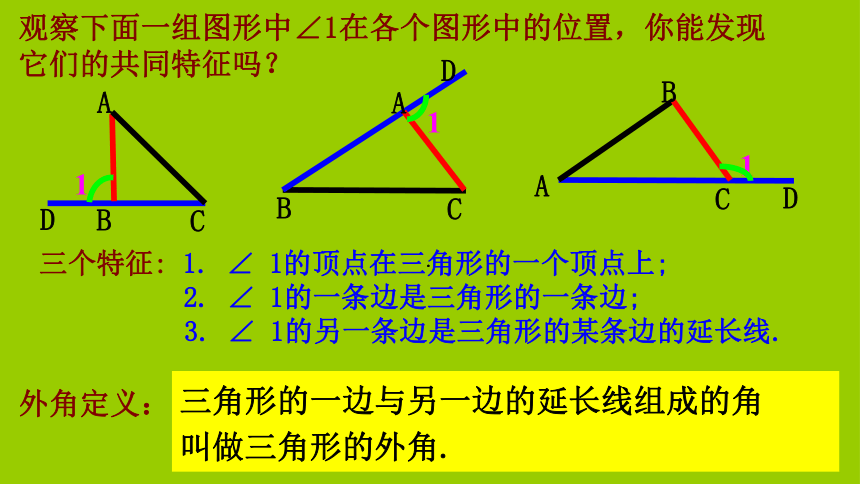
求证: ∠ADE=500..结论: 直角三角形的两个锐角互余.以后可以直接运用.观察下面一组图形中∠1在各个图形中的位置,你能发现它们的共同特征吗?外角定义:三角形的一边与另一边的延长线组成的角
叫做三角形的外角.三个特征: 1. ∠ 1的顶点在三角形的一个顶点上;
2. ∠ 1的一条边是三角形的一条边;
3. ∠ 1的另一条边是三角形的某条边的延长线.···大家一起画一画想一想:
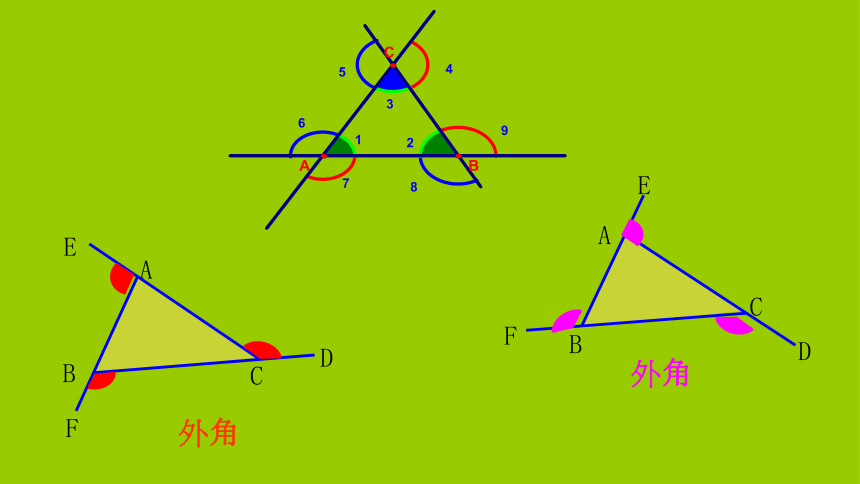
1、每一个三角形有几个外角?
2、每一个顶点处相对应的外角有几个?
3、这些外角中有几个外角相等? 4、三角形的每一个外角与三角形的三个内角有什么位置关系?
画一个三角形,再画出它所有的外角.归纳: 1、每一个三角形都有6个外角;2、每一个顶点相对应的外角都有2个; 4、一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.3、这6个外角中有3个外角相等.探究:
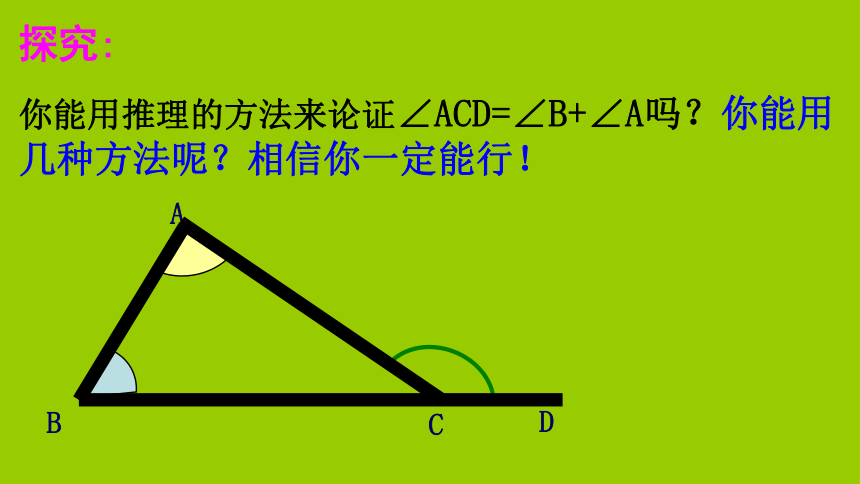
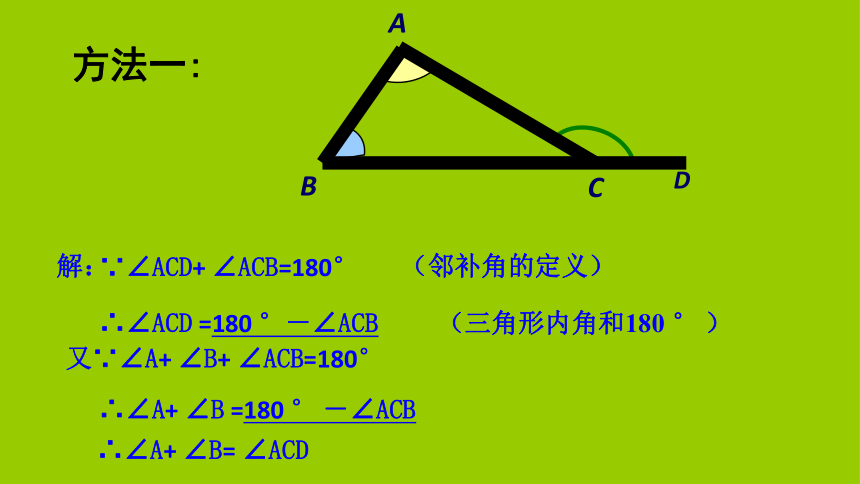
你能用推理的方法来论证∠ACD=∠B+∠A吗?你能用几种方法呢?相信你一定能行!D ∵∠ACD+ ∠ACB=180°又∵∠A+ ∠B+ ∠ACB=180° ∴∠A+ ∠B= ∠ACD 解:∴∠ACD =180 °-∠ACB ∴∠A+ ∠B =180 ° -∠ACB(邻补角的定义)(三角形内角和180 ° )方法一:1(作CE//BA)
由平行线的性质
把两个内角转换
可得
AE方法二:擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?哪位同学证明一下.CBD三角形的一个外角等于与它不相邻的两个内角的和 三角形的一个外角大于任何一个与它不相邻的内角.D∵∠ACD= ∠A+ ∠B∴∠ACD﹥∠A
∠ACD﹥ ∠B结论:3.三角形的一个外角与它不相邻的任意一个内角有怎样的大小关系?三角形外角的性质:
性质1、三角形的一个外角等于与它不相邻的两个内角的和. ∠B+∠C=∠CAD 性质2、三角形的一个外角大于任何一个与它不相邻的内角.
∠CAD > ∠B, ∠CAD > ∠C证明:∵∠EAC=∠B+∠C
(三角形的一个外角等于和它
不相邻的两个内角的和)
∠B=∠C (已知)
∴∠B= ∠EAC(等式性质)··例1 已知:如图在△ABC中,AD平分外角∠EAC,∠B=∠C. 求证:AD∥BC.∵ AD平分∠EAC(已知)
∴∠DAE= ∠EAC(角平分线的定义)∴∠DAE=∠B(等量代换)
∴ AD∥BC(同位角相等,两直线平行)例2 已知:如图,在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,连接DE.
求证: ∠1 >∠2.证明:∵ ∠1是△ABC 的一个外角 (已知)
∴ ∠1 >∠3 (三角形的一个外角大于任何一个和它不相邻的内角)
∵∠3是△CDE 的一个外角 (外角定义)
∴∠3 >∠2 (三角形的一个外角大于任何一个和它不相邻的内角)
∴ ∠1 >∠2 (不等式的性质)CAB1345ED2跟踪练习1.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定C 2.如图所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于( )
A.120° B.115° C.110° D.105°B4.如图所示,∠1=_______.120 °5.已知等腰三角形的一个外角为150°,则它的底角为_ ____. 30或75° 6.如图所示,∠A=50°,∠B=40°,∠C=30°,则∠BDC=________.120°7.已知:如图,在△ABC中,外角∠DCA=100°,
∠A=45°.求:∠B和∠ACB的大小.ABC解:∵ ∠DCA是△ABC的一个外角(已知), ∴ ∠B= ∠DCA-∠A=100°-45°=55° 又∵ ∠DCA+∠BCA=180°(平角=180°).∴ ∠ACB=80°(等式的性质).100°45°(三角形的一个外角等于和它不相邻的两个内角的和).当堂检测1△ABC 中,若∠A +∠B =∠C ,则△ABC 是( )
A.锐角△ B..直角△ C.钝角△ D.等腰△2 一个三角形至少有( )
A.一个锐角 B.两个锐角
C.一个钝角 D.一个直角BB证明:∵ ∠1 +∠4=180°
∠2 +∠5=180°
∠3 +∠6=180°
∴ ∠1+ ∠2 + ∠3 +∠4 +∠5 +∠6=3× 180°=540°
又∵ ∠4+ ∠5 + ∠6= 180° (三角形内角和定理)
∴ ∠1 +∠2 +∠3=540 °- 180°= 360°3.已知:∠1,∠2,∠3是△ABC 的三个外角.
求证:∠1+∠2+∠3=360°.4. 在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数.
解:在△ABC中,
∠A+∠B+∠C=180°,∠A=80°
∴∠B+∠C=100°
∵∠B=∠C
∴∠B=∠C=50°5. 已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数.
解:设三个内角度数分别为:x , 3x , 5x.
列出方程 x+3x+5x=180°
x=20°
答:三个内角度数分别为20°,60°,100°.三角形内角和定理
三角形三个内角的和等于180°.
△ABC中,∠A+∠B+∠C=180°.
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
求证: ∠ADE=500..结论: 直角三角形的两个锐角互余.以后可以直接运用.观察下面一组图形中∠1在各个图形中的位置,你能发现它们的共同特征吗?外角定义:三角形的一边与另一边的延长线组成的角
叫做三角形的外角.三个特征: 1. ∠ 1的顶点在三角形的一个顶点上;
2. ∠ 1的一条边是三角形的一条边;
3. ∠ 1的另一条边是三角形的某条边的延长线.···大家一起画一画想一想:
1、每一个三角形有几个外角?
2、每一个顶点处相对应的外角有几个?
3、这些外角中有几个外角相等? 4、三角形的每一个外角与三角形的三个内角有什么位置关系?
画一个三角形,再画出它所有的外角.归纳: 1、每一个三角形都有6个外角;2、每一个顶点相对应的外角都有2个; 4、一个三角形的每一个外角对应一个相邻的内角和两个不相邻的内角.3、这6个外角中有3个外角相等.探究:
你能用推理的方法来论证∠ACD=∠B+∠A吗?你能用几种方法呢?相信你一定能行!D ∵∠ACD+ ∠ACB=180°又∵∠A+ ∠B+ ∠ACB=180° ∴∠A+ ∠B= ∠ACD 解:∴∠ACD =180 °-∠ACB ∴∠A+ ∠B =180 ° -∠ACB(邻补角的定义)(三角形内角和180 ° )方法一:1(作CE//BA)
由平行线的性质
把两个内角转换
可得
AE方法二:擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?哪位同学证明一下.CBD三角形的一个外角等于与它不相邻的两个内角的和 三角形的一个外角大于任何一个与它不相邻的内角.D∵∠ACD= ∠A+ ∠B∴∠ACD﹥∠A
∠ACD﹥ ∠B结论:3.三角形的一个外角与它不相邻的任意一个内角有怎样的大小关系?三角形外角的性质:
性质1、三角形的一个外角等于与它不相邻的两个内角的和. ∠B+∠C=∠CAD 性质2、三角形的一个外角大于任何一个与它不相邻的内角.
∠CAD > ∠B, ∠CAD > ∠C证明:∵∠EAC=∠B+∠C
(三角形的一个外角等于和它
不相邻的两个内角的和)
∠B=∠C (已知)
∴∠B= ∠EAC(等式性质)··例1 已知:如图在△ABC中,AD平分外角∠EAC,∠B=∠C. 求证:AD∥BC.∵ AD平分∠EAC(已知)
∴∠DAE= ∠EAC(角平分线的定义)∴∠DAE=∠B(等量代换)
∴ AD∥BC(同位角相等,两直线平行)例2 已知:如图,在△ABC中, ∠1是它的一个外角, E为边AC上一点,延长BC到D,连接DE.
求证: ∠1 >∠2.证明:∵ ∠1是△ABC 的一个外角 (已知)
∴ ∠1 >∠3 (三角形的一个外角大于任何一个和它不相邻的内角)
∵∠3是△CDE 的一个外角 (外角定义)
∴∠3 >∠2 (三角形的一个外角大于任何一个和它不相邻的内角)
∴ ∠1 >∠2 (不等式的性质)CAB1345ED2跟踪练习1.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定C 2.如图所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于( )
A.120° B.115° C.110° D.105°B4.如图所示,∠1=_______.120 °5.已知等腰三角形的一个外角为150°,则它的底角为_ ____. 30或75° 6.如图所示,∠A=50°,∠B=40°,∠C=30°,则∠BDC=________.120°7.已知:如图,在△ABC中,外角∠DCA=100°,
∠A=45°.求:∠B和∠ACB的大小.ABC解:∵ ∠DCA是△ABC的一个外角(已知), ∴ ∠B= ∠DCA-∠A=100°-45°=55° 又∵ ∠DCA+∠BCA=180°(平角=180°).∴ ∠ACB=80°(等式的性质).100°45°(三角形的一个外角等于和它不相邻的两个内角的和).当堂检测1△ABC 中,若∠A +∠B =∠C ,则△ABC 是( )
A.锐角△ B..直角△ C.钝角△ D.等腰△2 一个三角形至少有( )
A.一个锐角 B.两个锐角
C.一个钝角 D.一个直角BB证明:∵ ∠1 +∠4=180°
∠2 +∠5=180°
∠3 +∠6=180°
∴ ∠1+ ∠2 + ∠3 +∠4 +∠5 +∠6=3× 180°=540°
又∵ ∠4+ ∠5 + ∠6= 180° (三角形内角和定理)
∴ ∠1 +∠2 +∠3=540 °- 180°= 360°3.已知:∠1,∠2,∠3是△ABC 的三个外角.
求证:∠1+∠2+∠3=360°.4. 在△ABC中,∠A=80°,∠B=∠C , 求∠C的度数.
解:在△ABC中,
∠A+∠B+∠C=180°,∠A=80°
∴∠B+∠C=100°
∵∠B=∠C
∴∠B=∠C=50°5. 已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数.
解:设三个内角度数分别为:x , 3x , 5x.
列出方程 x+3x+5x=180°
x=20°
答:三个内角度数分别为20°,60°,100°.三角形内角和定理
三角形三个内角的和等于180°.
△ABC中,∠A+∠B+∠C=180°.
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
