北京市大兴区2024~2025学年第一学期初二期中数学试题(pdf版,含答案)
文档属性
| 名称 | 北京市大兴区2024~2025学年第一学期初二期中数学试题(pdf版,含答案) |  | |
| 格式 | |||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-05 21:24:10 | ||
图片预览




文档简介
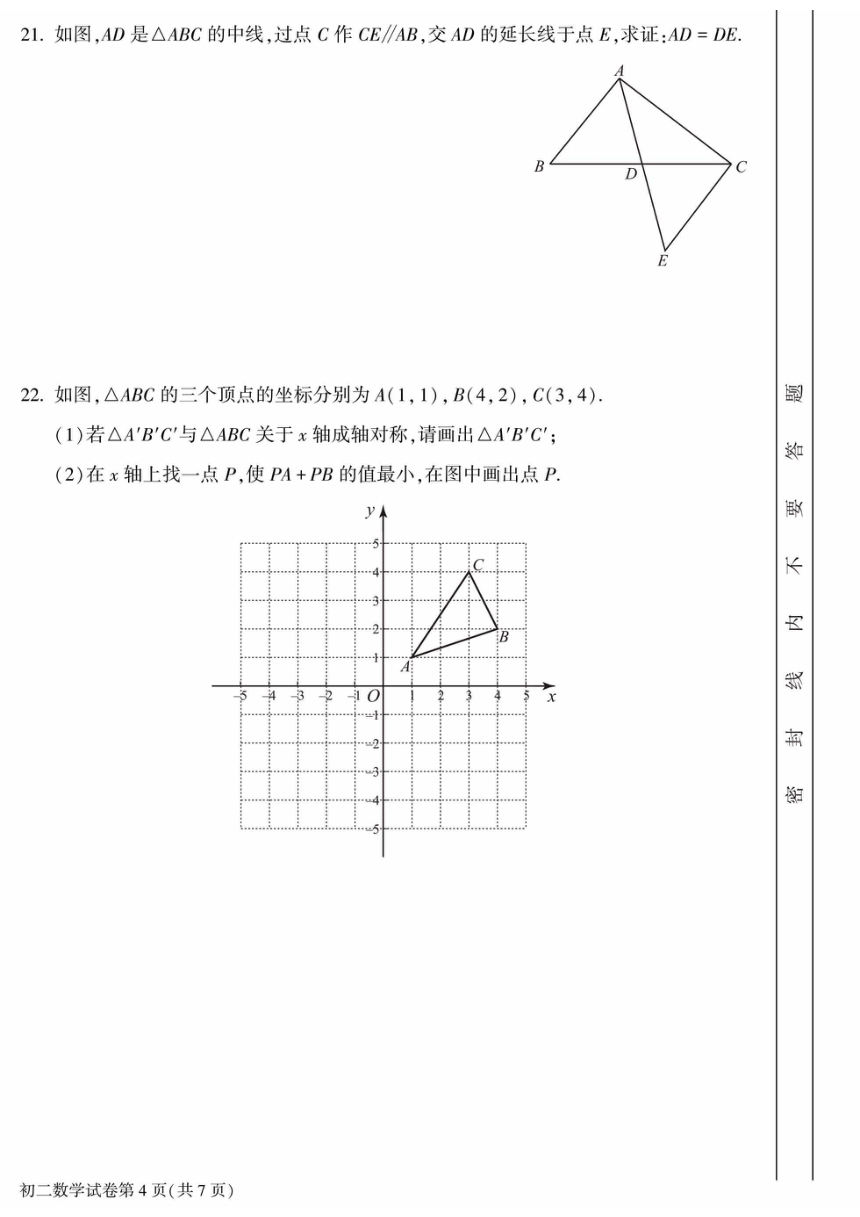
大兴区 2024~2025 学年度第一学期期中检测
初二数学参考答案及评分标准
一、选择题(共 16 分,每题 2 分)
题号 1 2 3 4 5 6 7 8
答案 A D B A C B C B
二、填空题(共 16 分,每题 2 分)
9. 4 3x
10.(-2,-1)
1
11. x
2
12. x = 3
13.3
14.答案不唯一,如 AB=AD
a
15.
4
16.30°或 110°
三、解答题(共 68 分,第 17-22 题,每题 5 分,第 23-26 题,每题 6 分,第 27-28 题,每题 7 分)
17.解: | 2 1| + 49 3 8 ( 2 2)
= 2 1+ 7 2 + 2 2 ………………………………………………………………………………4 分
=3 2 + 4 ……………………………………………………………………………………………5 分
(3 x 1) 4 + 2x ①
18.解: x 9
2x ②
5
解不等式①得: x 7 …………………………………………………………………………………2 分
解不等式②得: x 1 …………………………………………………………………………………4 分
∴原不等式组的解解集是 1 x 7. ………………………………………………………………5 分
19.证明:∵在△ABO 和△ACO 中,
初一数学参考答案及评分标准 第1页(共 7 页)
AB = AC
BO = CO
AO = AO
∴△ABO≌△ACO, …………………………………………………………………………………3 分
∴∠BAO=∠CAO,
∴AO 平分∠BAC.……………………………………………………………………………………5 分
20.(1)解:
……………………………………………………………………2 分
(2)证明:
∵AP 平分∠BAC,
∴∠BAP=∠CAP,……………………………………………………………………………………3 分
在△ABP 和△ADP 中,
AB = AD
BAP = CAP
AP = AP
∴△ABP≌△ADP. …………………………………………………………………………………4 分
∴PB=PD.……………………………………………………………………………………………5 分
21.证明:
初一数学参考答案及评分标准 第2页(共 7 页)
证明:∵AD 是△ABC 的中线,
∴BD=CD,………………………………………………………………………………………………1 分
∵AB∥CE,
∴∠BAD=∠E……………………………………………………………………………………………2分
在△ABD 和△ECD 中,
BAD = E
BDA = CDE
BD = CD
∴△ABD≌△ECD. ……………………………………………………………………………………4 分
∴AD=DE.………………………………………………………………………………………………5 分
(方法不唯一)
22.解:
……………………………………………………………5 分
(第二问,也还可以连接 AB’,与 x 轴交点也是 P 点)
23.解:(1)
初一数学参考答案及评分标准 第3页(共 7 页)
. ………………………………………………………………………1 分
(2)CD;
线段垂直平分线上的点与这条线段两个端点的距离相等;
AC;
CD;
等边对等角.……………………………………………………………………………………………6 分
24.解:(1)2-m; ……………………………………………………………………………………1 分
(2) f (x) = mx3 2mx + x m,
f (0) = m 03 2m 02 + 0 m = m.
f (0) = 0,
m = 0,
m = 0.
把m = 0代入f (x) = mx3 2mx + x m,
f (x) = x,
f (2024) = 2024.. 3分
(3) f (x) = mx3 2mx + x m,
f (1) = m 2m +1 m = 2m +1,
f ( 1) = m 2m 1 m = 4m 1.
f (1)≤f ( 1),
2m +1≤ 4m 1.
m≤ 1.. 6分
25.解:在 CD 上截取CE = CB ,连接 AE.
∵AC 平分∠BCD,
初一数学参考答案及评分标准 第4页(共 7 页)
∴∠1=∠2. ……………………………………………… 1 分
在△AEC 和△ABC 中,
CE = CB
1= 2
AC = AC
∴△AEC≌△ABC.
∴∠3=∠B,AE=
AB. ……………………………………………………………………………… 3 分
∵AB=AD,
∴AE=AD.
∴∠4=∠D.
∵ 3+ 4 =180 ,
∴ B + D =180 ……………………………………………………………………………………… 4 分
∵在四边形 ABCD 中,
BAD + B + BCD + D = 360 ,
∴ BAD + BCD =180 .
∵ BAD = 90 ,
∴ BCD = 90 .………………………………………………………………………………………… 5 分
∵ 1= 2,
∴ 2 = 45 ,
即 ACB = 45 .……………………………………………
…………………………………………… 6 分
26.(1)证明:连接 AD.
∵Rt△ABC 向左平移两个单位得到 Rt△DEF,
∴AD∥BC,AD=CF=2,
∴∠MAD=∠MBF. ………………………1 分
∵B(1,0),C(5,0),
∴BC=4,
∴BF=BC-CF=2,
∴BF=AD. ………………………………………………………………………………………………2 分
初一数学参考答案及评分标准 第5页(共 7 页)
∵∠DMA=∠FMB,
∴△DMA≌△FMB,
∴AM=BM. ……………………………………………………………………………………………3 分
(2)①过点 N 作 NH⊥BC 于 H,NG⊥AC 于 G.
∵A(5,2),C(5,0),
∴AC=2,
∴AC=AD,
∴∠ADC=∠ACD. ……………………………………………………………………………………4 分
∵AD∥CB,
∴∠DAC+∠ACB=180°.
∵∠ACB=90°,
∴∠DAC=90°,
∴∠ACD+∠ADC=90°,
∴∠ACD=45°,
∴∠BCD=45°,
∴CD 为∠ACB 的平分线. ……………………………………………………………………………5 分
4
② . ……………………………………………………………………………………………………6 分
3
27.解:(1)∵∠DAE=60°,AD=AE,
∴△ADE 是等边三角形;………………………………………………………………………………1 分
(2)①证明:延长 BC 至点 G,使 BC=CG,连接 AG,EG,
∵BC=CG,∠C=90°,
∴AB=AG.
∵∠ACB=90°,∠BAC=30°,
∴∠ABC=60°.
∴△ABG 是等边三角形,∠ABD=120°.
∴∠AGB=∠BAG=60°.
∴∠DAE=∠BAG=60°.
∴∠DAB=∠EAG.
在△ABD 和△AGE 中
初一数学参考答案及评分标准 第6页(共 7 页)
AD=AE
DAB = EAG
AB = AG
∴△ABD≌△AGE
∴BD=GE,∠ABD=∠AGE=120°.
∵∠AGB=60°,
∴∠EGC=60°.
∴∠EGC=∠ABC.
在△BCF 和△GCE 中
∠ABC=∠EGC
BC = GC
BCF = GCE
∴△BCF≌△GCE,
∴BF=EG,
∴BD=BF.
②AB=2(CD-BF).……………………………………………………………………………………6 分
(3)AB=2(CD+BF). ………………………………………………………………………………7 分
28.解:(1)点 Q1(-2,7) ;……………………………………………………………………………2 分
(2)∵点 P2(﹣1,t﹣1),
∴点 Q2(1,t-3),
∴ t 3 = 0
∴ t = 3;…………………………………………………………………………………………………5 分
(3) t≥3 或 t≤ 3 .……………………………………………………………………………………7 分
初一数学参考答案及评分标准 第7页(共 7 页)
初二数学参考答案及评分标准
一、选择题(共 16 分,每题 2 分)
题号 1 2 3 4 5 6 7 8
答案 A D B A C B C B
二、填空题(共 16 分,每题 2 分)
9. 4 3x
10.(-2,-1)
1
11. x
2
12. x = 3
13.3
14.答案不唯一,如 AB=AD
a
15.
4
16.30°或 110°
三、解答题(共 68 分,第 17-22 题,每题 5 分,第 23-26 题,每题 6 分,第 27-28 题,每题 7 分)
17.解: | 2 1| + 49 3 8 ( 2 2)
= 2 1+ 7 2 + 2 2 ………………………………………………………………………………4 分
=3 2 + 4 ……………………………………………………………………………………………5 分
(3 x 1) 4 + 2x ①
18.解: x 9
2x ②
5
解不等式①得: x 7 …………………………………………………………………………………2 分
解不等式②得: x 1 …………………………………………………………………………………4 分
∴原不等式组的解解集是 1 x 7. ………………………………………………………………5 分
19.证明:∵在△ABO 和△ACO 中,
初一数学参考答案及评分标准 第1页(共 7 页)
AB = AC
BO = CO
AO = AO
∴△ABO≌△ACO, …………………………………………………………………………………3 分
∴∠BAO=∠CAO,
∴AO 平分∠BAC.……………………………………………………………………………………5 分
20.(1)解:
……………………………………………………………………2 分
(2)证明:
∵AP 平分∠BAC,
∴∠BAP=∠CAP,……………………………………………………………………………………3 分
在△ABP 和△ADP 中,
AB = AD
BAP = CAP
AP = AP
∴△ABP≌△ADP. …………………………………………………………………………………4 分
∴PB=PD.……………………………………………………………………………………………5 分
21.证明:
初一数学参考答案及评分标准 第2页(共 7 页)
证明:∵AD 是△ABC 的中线,
∴BD=CD,………………………………………………………………………………………………1 分
∵AB∥CE,
∴∠BAD=∠E……………………………………………………………………………………………2分
在△ABD 和△ECD 中,
BAD = E
BDA = CDE
BD = CD
∴△ABD≌△ECD. ……………………………………………………………………………………4 分
∴AD=DE.………………………………………………………………………………………………5 分
(方法不唯一)
22.解:
……………………………………………………………5 分
(第二问,也还可以连接 AB’,与 x 轴交点也是 P 点)
23.解:(1)
初一数学参考答案及评分标准 第3页(共 7 页)
. ………………………………………………………………………1 分
(2)CD;
线段垂直平分线上的点与这条线段两个端点的距离相等;
AC;
CD;
等边对等角.……………………………………………………………………………………………6 分
24.解:(1)2-m; ……………………………………………………………………………………1 分
(2) f (x) = mx3 2mx + x m,
f (0) = m 03 2m 02 + 0 m = m.
f (0) = 0,
m = 0,
m = 0.
把m = 0代入f (x) = mx3 2mx + x m,
f (x) = x,
f (2024) = 2024.. 3分
(3) f (x) = mx3 2mx + x m,
f (1) = m 2m +1 m = 2m +1,
f ( 1) = m 2m 1 m = 4m 1.
f (1)≤f ( 1),
2m +1≤ 4m 1.
m≤ 1.. 6分
25.解:在 CD 上截取CE = CB ,连接 AE.
∵AC 平分∠BCD,
初一数学参考答案及评分标准 第4页(共 7 页)
∴∠1=∠2. ……………………………………………… 1 分
在△AEC 和△ABC 中,
CE = CB
1= 2
AC = AC
∴△AEC≌△ABC.
∴∠3=∠B,AE=
AB. ……………………………………………………………………………… 3 分
∵AB=AD,
∴AE=AD.
∴∠4=∠D.
∵ 3+ 4 =180 ,
∴ B + D =180 ……………………………………………………………………………………… 4 分
∵在四边形 ABCD 中,
BAD + B + BCD + D = 360 ,
∴ BAD + BCD =180 .
∵ BAD = 90 ,
∴ BCD = 90 .………………………………………………………………………………………… 5 分
∵ 1= 2,
∴ 2 = 45 ,
即 ACB = 45 .……………………………………………
…………………………………………… 6 分
26.(1)证明:连接 AD.
∵Rt△ABC 向左平移两个单位得到 Rt△DEF,
∴AD∥BC,AD=CF=2,
∴∠MAD=∠MBF. ………………………1 分
∵B(1,0),C(5,0),
∴BC=4,
∴BF=BC-CF=2,
∴BF=AD. ………………………………………………………………………………………………2 分
初一数学参考答案及评分标准 第5页(共 7 页)
∵∠DMA=∠FMB,
∴△DMA≌△FMB,
∴AM=BM. ……………………………………………………………………………………………3 分
(2)①过点 N 作 NH⊥BC 于 H,NG⊥AC 于 G.
∵A(5,2),C(5,0),
∴AC=2,
∴AC=AD,
∴∠ADC=∠ACD. ……………………………………………………………………………………4 分
∵AD∥CB,
∴∠DAC+∠ACB=180°.
∵∠ACB=90°,
∴∠DAC=90°,
∴∠ACD+∠ADC=90°,
∴∠ACD=45°,
∴∠BCD=45°,
∴CD 为∠ACB 的平分线. ……………………………………………………………………………5 分
4
② . ……………………………………………………………………………………………………6 分
3
27.解:(1)∵∠DAE=60°,AD=AE,
∴△ADE 是等边三角形;………………………………………………………………………………1 分
(2)①证明:延长 BC 至点 G,使 BC=CG,连接 AG,EG,
∵BC=CG,∠C=90°,
∴AB=AG.
∵∠ACB=90°,∠BAC=30°,
∴∠ABC=60°.
∴△ABG 是等边三角形,∠ABD=120°.
∴∠AGB=∠BAG=60°.
∴∠DAE=∠BAG=60°.
∴∠DAB=∠EAG.
在△ABD 和△AGE 中
初一数学参考答案及评分标准 第6页(共 7 页)
AD=AE
DAB = EAG
AB = AG
∴△ABD≌△AGE
∴BD=GE,∠ABD=∠AGE=120°.
∵∠AGB=60°,
∴∠EGC=60°.
∴∠EGC=∠ABC.
在△BCF 和△GCE 中
∠ABC=∠EGC
BC = GC
BCF = GCE
∴△BCF≌△GCE,
∴BF=EG,
∴BD=BF.
②AB=2(CD-BF).……………………………………………………………………………………6 分
(3)AB=2(CD+BF). ………………………………………………………………………………7 分
28.解:(1)点 Q1(-2,7) ;……………………………………………………………………………2 分
(2)∵点 P2(﹣1,t﹣1),
∴点 Q2(1,t-3),
∴ t 3 = 0
∴ t = 3;…………………………………………………………………………………………………5 分
(3) t≥3 或 t≤ 3 .……………………………………………………………………………………7 分
初一数学参考答案及评分标准 第7页(共 7 页)
同课章节目录
