24.1 圆的有关性质 基础练习(含答案)2024-2025学年人教版九年级数学上册
文档属性
| 名称 | 24.1 圆的有关性质 基础练习(含答案)2024-2025学年人教版九年级数学上册 | 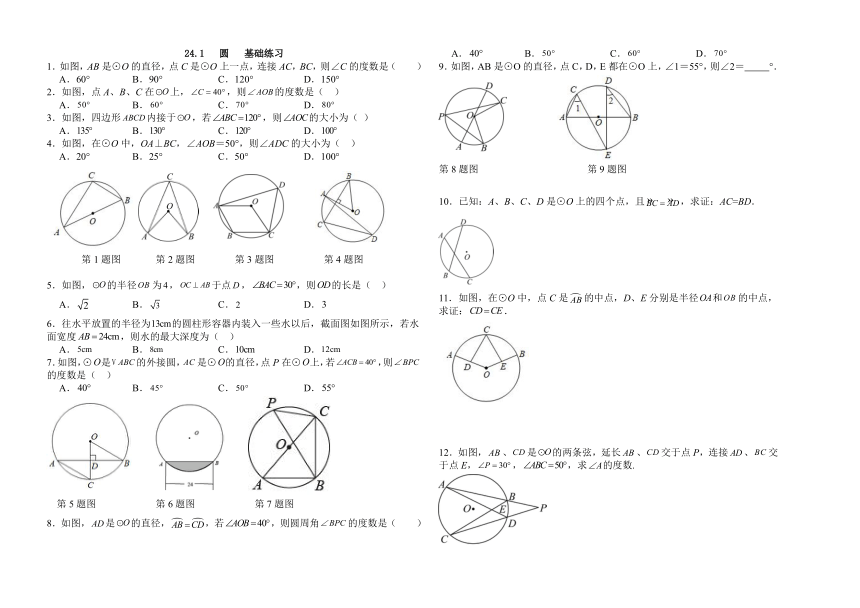 | |
| 格式 | docx | ||
| 文件大小 | 622.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-05 22:42:14 | ||
图片预览


文档简介
24.1 圆 基础练习
1.如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,BC,则∠C的度数是( )
A.60° B.90° C.120° D.150°
2.如图,点A、B、C在上,,则的度数是( )
A. B. C. D.
3.如图,四边形内接于,若,则的大小为( )
A. B. C. D.
4.如图,在⊙O中,OA⊥BC,∠AOB=50°,则∠ADC的大小为( )
A.20° B.25° C.50° D.100°
第1题图 第2题图 第3题图 第4题图
5.如图,的半径为,于点,,则的长是( )
A. B. C. D.
6.往水平放置的半径为的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度,则水的最大深度为( )
A. B. C. D.
7.如图,⊙是的外接圆,是⊙的直径,点P在⊙上,若,则的度数是( )
A. B. C. D.
第5题图 第6题图 第7题图
8.如图,是的直径,,若,则圆周角的度数是( )
A. B. C. D.
9.如图,AB是⊙O的直径,点C,D,E都在⊙O上,∠1=55°,则∠2= °.
第8题图 第9题图
10.已知:A、B、C、D是⊙O上的四个点,且,求证:AC=BD.
11.如图,在⊙O中,点C是的中点,D、E分别是半径和的中点,求证:.
12.如图,、是的两条弦,延长、交于点P,连接、交于点E,,,求的度数.
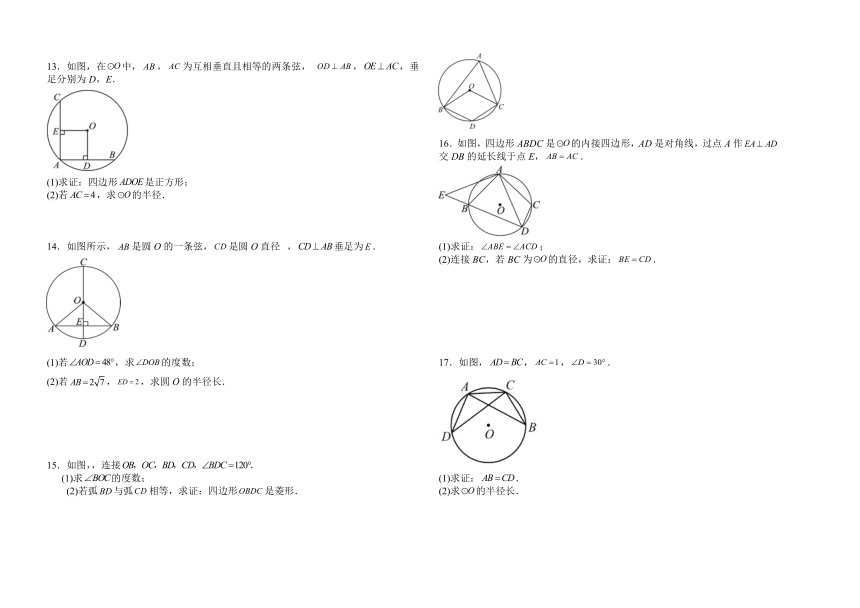
13.如图,在中,,为互相垂直且相等的两条弦, ,,垂足分别为D,E.
(1)求证:四边形是正方形;
(2)若,求的半径.
14.如图所示,是圆O的一条弦,是圆O直径,垂足为.
(1)若,求的度数;
(2)若,,求圆O的半径长.
如图,,连接
(1)求的度数;
(2)若弧与弧相等,求证:四边形是菱形.
16.如图,四边形ABDC是的内接四边形,AD是对角线,过点A作交DB的延长线于点E,.
(1)求证:;
(2)连接BC,若BC为的直径,求证:.
17.如图,,,.
(1)求证:.
(2)求的半径长.
18.如图,AB是⊙O的弦,过圆心O作OC⊥AB,垂足为点C,且交⊙O于点D,AB=6,CD=2,求⊙O的半径长度.
19.如图,已知为的直径,是弦,且于点.连接,,.
(1)求证:;
(2)若,,求的直径.
20.如图,已知AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上,连接OA、DE、BE.
(1)若∠AOD=60°,求∠DEB的度数;
(2)若CD=2,弦AB=8,求⊙O的半径长.
参考答案:
题号 1 2 3 4 5 6 7 8
答案 B D C B C B C B
9.35
10.证明:∵
∴
∴
11.证明:连接,如图所示:
∵,且D、E分别是半径和的中点,
∴,
∵C是的中点,
∴,
∴,
∴在和中,
,
∴(SAS),
∴.
12.解:∵为的外角,,,
∴,
∵,
∴.
13(1)证明:证明:∵,,
∴,
∵,为互相垂直且相等的两条弦,
∴,
∵,
∴四边形是矩形;
∵,
∴四边形是正方形;
(2)解:连接,如图所示
∵
∴
由(1)知四边形是正方形;
则
在中,
所以的半径是.
14.(1)解:是圆的一条弦,,
,
,
的度数是;
(2)解:是圆的一条弦,,
,
设圆的半径长为,
在中,,
,
,
∴圆的半径长为.
15.(1)∵四边形内接于,
∴
∴
(2)解:如图:连接
∵弧与弧相等
∴
∵,
∴
∵
∴等边三角形,
∴
四边形是菱形;
握相关性质内容是解题的关键.
16.(1)证明:∵四边形ABDC是的内接四边形,
∴,
∵,
∴;
(2)连接BC,
∵BC为的直径,
∴,
∵,
∴,
∴,
∴,
在和中,
,
∴(ASA),
∴.
17.(1)解:∵在中,,
∴,
又∵,都是所对的圆周角,
∴,
∵AC=AC
∴,
∴.
(2)解:如图,连接,,
∵,
∴,
∵,
∴是等边三角形,
∴,
∴的半径长为1.
18.解:∵是⊙O的弦,OC⊥AB,
∴,
又∵AB=6,
∴AC=3,
设⊙O的半径是r,则有OA=r,
CD=2,
OC=r-CD=r-2,
在Rt△OAC中,,
∴,
解得,
即⊙O的半径是.
19.(1)证明见解析;(2).
证明:(1)∵为的直径,是弦,且于,
∴,,
∴
∵,
∴,
∴.
(2)设的半径为,
在中,
,
.
则,
在中,
,
∴,
∴.
∴.
答:的直径为.
20.解:(1)∵OD⊥AB,
∴=,
∴∠BOD=∠AOD=60°,
∴∠DEB=∠BOD=×60°=30°;
(2)设⊙O的半径为r,则OC=r﹣2,
∵OD⊥AB,
∴AC=BC=AB=×8=4,
在Rt△OAC中,由勾股定理得:(r﹣2)2+42=r2,
解得:r=5,
即⊙O的半径长为5.
1.如图,AB是⊙O的直径,点C是⊙O上一点,连接AC,BC,则∠C的度数是( )
A.60° B.90° C.120° D.150°
2.如图,点A、B、C在上,,则的度数是( )
A. B. C. D.
3.如图,四边形内接于,若,则的大小为( )
A. B. C. D.
4.如图,在⊙O中,OA⊥BC,∠AOB=50°,则∠ADC的大小为( )
A.20° B.25° C.50° D.100°
第1题图 第2题图 第3题图 第4题图
5.如图,的半径为,于点,,则的长是( )
A. B. C. D.
6.往水平放置的半径为的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度,则水的最大深度为( )
A. B. C. D.
7.如图,⊙是的外接圆,是⊙的直径,点P在⊙上,若,则的度数是( )
A. B. C. D.
第5题图 第6题图 第7题图
8.如图,是的直径,,若,则圆周角的度数是( )
A. B. C. D.
9.如图,AB是⊙O的直径,点C,D,E都在⊙O上,∠1=55°,则∠2= °.
第8题图 第9题图
10.已知:A、B、C、D是⊙O上的四个点,且,求证:AC=BD.
11.如图,在⊙O中,点C是的中点,D、E分别是半径和的中点,求证:.
12.如图,、是的两条弦,延长、交于点P,连接、交于点E,,,求的度数.
13.如图,在中,,为互相垂直且相等的两条弦, ,,垂足分别为D,E.
(1)求证:四边形是正方形;
(2)若,求的半径.
14.如图所示,是圆O的一条弦,是圆O直径,垂足为.
(1)若,求的度数;
(2)若,,求圆O的半径长.
如图,,连接
(1)求的度数;
(2)若弧与弧相等,求证:四边形是菱形.
16.如图,四边形ABDC是的内接四边形,AD是对角线,过点A作交DB的延长线于点E,.
(1)求证:;
(2)连接BC,若BC为的直径,求证:.
17.如图,,,.
(1)求证:.
(2)求的半径长.
18.如图,AB是⊙O的弦,过圆心O作OC⊥AB,垂足为点C,且交⊙O于点D,AB=6,CD=2,求⊙O的半径长度.
19.如图,已知为的直径,是弦,且于点.连接,,.
(1)求证:;
(2)若,,求的直径.
20.如图,已知AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上,连接OA、DE、BE.
(1)若∠AOD=60°,求∠DEB的度数;
(2)若CD=2,弦AB=8,求⊙O的半径长.
参考答案:
题号 1 2 3 4 5 6 7 8
答案 B D C B C B C B
9.35
10.证明:∵
∴
∴
11.证明:连接,如图所示:
∵,且D、E分别是半径和的中点,
∴,
∵C是的中点,
∴,
∴,
∴在和中,
,
∴(SAS),
∴.
12.解:∵为的外角,,,
∴,
∵,
∴.
13(1)证明:证明:∵,,
∴,
∵,为互相垂直且相等的两条弦,
∴,
∵,
∴四边形是矩形;
∵,
∴四边形是正方形;
(2)解:连接,如图所示
∵
∴
由(1)知四边形是正方形;
则
在中,
所以的半径是.
14.(1)解:是圆的一条弦,,
,
,
的度数是;
(2)解:是圆的一条弦,,
,
设圆的半径长为,
在中,,
,
,
∴圆的半径长为.
15.(1)∵四边形内接于,
∴
∴
(2)解:如图:连接
∵弧与弧相等
∴
∵,
∴
∵
∴等边三角形,
∴
四边形是菱形;
握相关性质内容是解题的关键.
16.(1)证明:∵四边形ABDC是的内接四边形,
∴,
∵,
∴;
(2)连接BC,
∵BC为的直径,
∴,
∵,
∴,
∴,
∴,
在和中,
,
∴(ASA),
∴.
17.(1)解:∵在中,,
∴,
又∵,都是所对的圆周角,
∴,
∵AC=AC
∴,
∴.
(2)解:如图,连接,,
∵,
∴,
∵,
∴是等边三角形,
∴,
∴的半径长为1.
18.解:∵是⊙O的弦,OC⊥AB,
∴,
又∵AB=6,
∴AC=3,
设⊙O的半径是r,则有OA=r,
CD=2,
OC=r-CD=r-2,
在Rt△OAC中,,
∴,
解得,
即⊙O的半径是.
19.(1)证明见解析;(2).
证明:(1)∵为的直径,是弦,且于,
∴,,
∴
∵,
∴,
∴.
(2)设的半径为,
在中,
,
.
则,
在中,
,
∴,
∴.
∴.
答:的直径为.
20.解:(1)∵OD⊥AB,
∴=,
∴∠BOD=∠AOD=60°,
∴∠DEB=∠BOD=×60°=30°;
(2)设⊙O的半径为r,则OC=r﹣2,
∵OD⊥AB,
∴AC=BC=AB=×8=4,
在Rt△OAC中,由勾股定理得:(r﹣2)2+42=r2,
解得:r=5,
即⊙O的半径长为5.
同课章节目录
