2024-2025学年苏科版数学八年级上册期中复习试题(无答案)
文档属性
| 名称 | 2024-2025学年苏科版数学八年级上册期中复习试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 474.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-05 22:44:29 | ||
图片预览

文档简介
2024-2025学年第一学期期中复习试题
初二数学
一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是正确的,请用2B铅笔把答题卡上相应的选项标号涂黑)
1. 下列四个图案中,是轴对称图形的是( )
A. B. C. D.
2. 如图,∠ABC=∠DCB,要说明△ABC≌△DCB,添加的条件不能是( )
A. AC=DB B. ∠A=∠D
C. BE=CE D. AB=DC
3. 等腰三角形的周长为,其中一边长为,则该等腰三角形的底边为( )
A. 或 B. 或 C. D.
4. 已知等腰三角形的两边长分别为3和4,则该等腰三角形的周长为( )
A. 10 B. 11 C. 10或11 D. 12
5. 下列说法正确的是( )
A. 4的平方根是2 B. 的立方根是
C. 没有平方根 D. 2是4的一个平方根
6. 如图,在和中,,,要使得,还需要补充一个条件,则下列错误条件是( )
A. B. C. D.
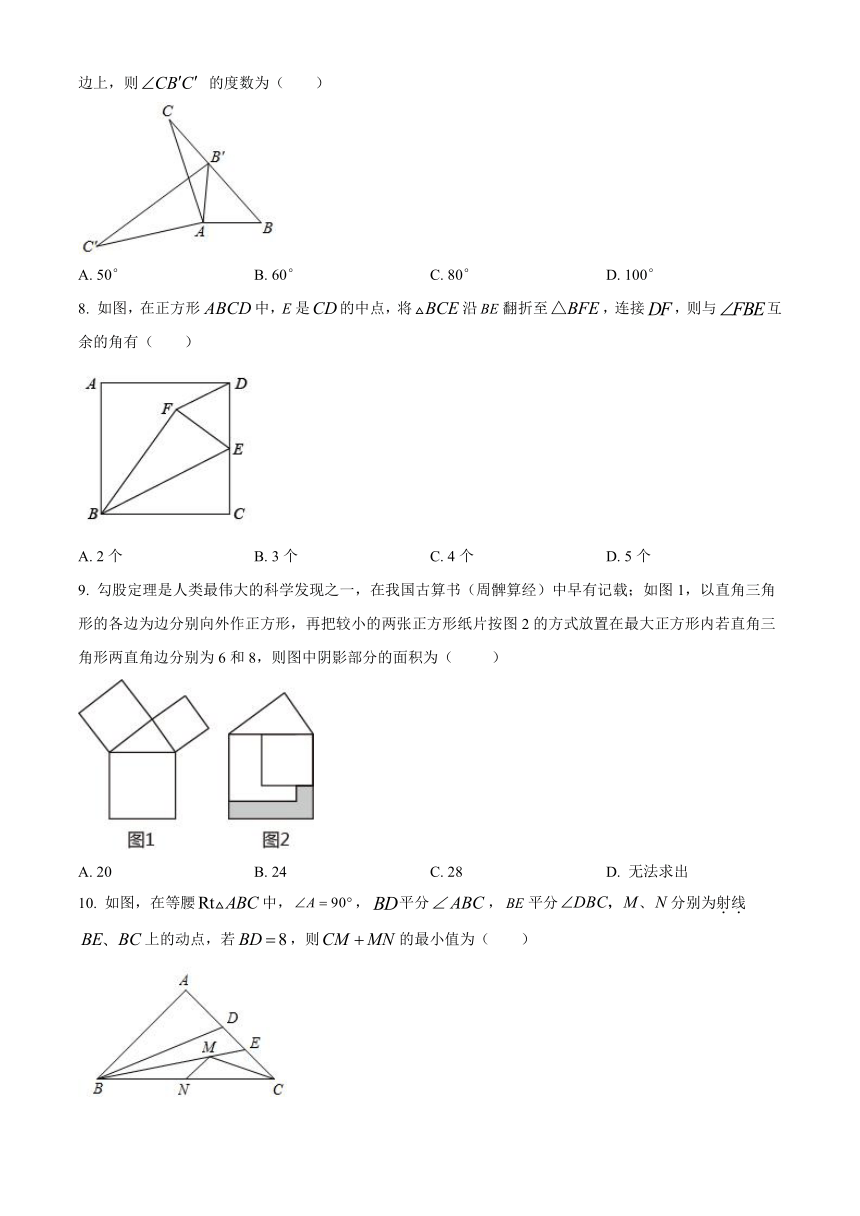
7. 如图,在△ABC中,∠B=50°,将△ABC绕点A按逆时针方向旋转得到.若点B′恰好落在BC边上,则 的度数为( )
A. 50° B. 60° C. 80° D. 100°
8. 如图,在正方形中,E是的中点,将沿翻折至,连接,则与互余的角有( )
A. 2个 B. 3个 C. 4个 D. 5个
9. 勾股定理是人类最伟大的科学发现之一,在我国古算书(周髀算经)中早有记载;如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内若直角三角形两直角边分别为6和8,则图中阴影部分的面积为( )
A. 20 B. 24 C. 28 D. 无法求出
10. 如图,在等腰中,,平分,平分分别为射线上的动点,若,则的最小值为( )
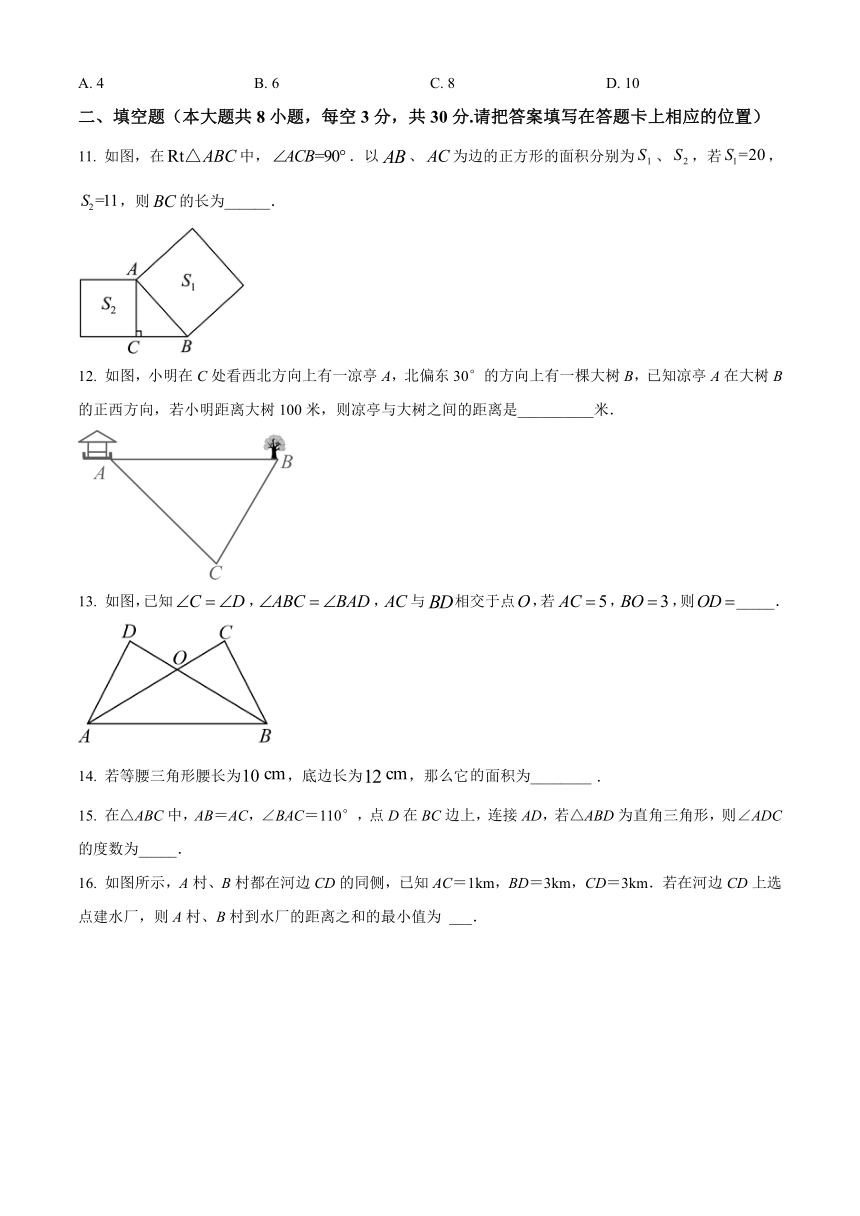
A. 4 B. 6 C. 8 D. 10
二、填空题(本大题共8小题,每空3分,共30分.请把答案填写在答题卡上相应的位置)
11. 如图,在中,.以、为边的正方形的面积分别为、,若,,则的长为______.
12. 如图,小明在C处看西北方向上有一凉亭A,北偏东30°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若小明距离大树100米,则凉亭与大树之间的距离是__________米.
13. 如图,已知,,与相交于点,若,,则_____.
14. 若等腰三角形腰长为,底边长为,那么它面积为________.
15. 在△ABC中,AB=AC,∠BAC=110°,点D在BC边上,连接AD,若△ABD为直角三角形,则∠ADC的度数为_____.
16. 如图所示,A村、B村都在河边CD的同侧,已知AC=1km,BD=3km,CD=3km.若在河边CD上选点建水厂,则A村、B村到水厂的距离之和的最小值为 ___.
17. 已知中,,,,将它一条直角边沿一锐角角平分线所在直线翻折,使直角顶点落在斜边上点D处,折痕交另一直角边于点E,则折叠后不重合部分三角形的周长为______.
18. 如图,在等腰三角形ACB中,AC=BC=10,AB=16,D为底边AB上一动点(不与点A,B重合),DE⊥AC,DF⊥BC,垂足分别为点E,F,则DE+DF等于_____.
三、解答题(本大题共9小题,共60分)
19. 如图,已知AB=DC,ABCD,E、F是AC上两点,且AF=CE.求证:△ABE≌△CDF.
20. 如图,AB=AC,AC的垂直平分线交AB于D,交AC于E.
(1)若∠A=40°,求∠BCD的度数;
(2)若AE=5,△BCD周长17,求△ABC的周长.
21. 如图,四边形ABCD中,ADBC,E为CD的中点,连结BE并延长交AD的延长线于点F,
(1)求证:△BCE≌△FDE;
(2)连结AE,当AE⊥BF,BC=2,AD=1时,求AB的长.
22. 小明和小亮学习了“勾股定理”之后,为了测量风筝的垂直高度,他们进行了如下操作:①测得水平距离的长为15米;②根据手中剩余线的长度计算出风筝线的长为25米;③牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度;
(2)如果小明想风筝沿方向下降12米,则他应该往回收线多少米?
23. 如图所示,在等腰ABC中,AB=AC,AF为BC的中线,D为AF上的一点,且BD的垂直平分线过点C并交BD于E,求证:BCD是等边三角形.
24. (1)如图1,已知:在ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E. 证明:DE=BD+CE.(提示:由于DE=AD+AE,证明AD=CE,AE=BD即可)
(2)如图2,将(1)中条件改为:在ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=,其中为任意钝角,请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且ABF和ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试证明DEF是等边三角形.
25. 如图1,在中,,动点以每秒的速度从点出发,沿线段向点运动.设点的运动时间为秒.
(知识储备:一个角是的等腰三角形是等边三角形.直角三角形中角所对的边等于斜边的一半.).
(1)当时,求证:是直角三角形.
(2)如图2,若另一动点在线段上以每秒的速度由点向点运动,且与点同时出发,点到达终点时点也随之停止运动.当是直角三角形时,直接写出的值.
(3)如图3,若另一动点从点出发,以每秒的速度沿射线方向运动,且与点同时出发.当点到达终点时点也随之停止运动,连接交于点,过点作于.在运动过程中,线段的长度是否发生变化?为什么?
26. 已知:如图,在中,,,点C、D分别是直线上一个动点.
(1)若是等腰三角形,用直尺和圆规作出点C(不写作法,保留作图痕迹),直接写出的长;
(2)若,求的长;
(3)将沿过中点E的直线翻折,点A落点记为Q,设折痕为,若折叠后长为4,则长为 .(直接写出答案,不需要解答过程)
初二数学
一、选择题(本大题共10小题,每小题3分,共30分.在每小题所给出的四个选项中,只有一项是正确的,请用2B铅笔把答题卡上相应的选项标号涂黑)
1. 下列四个图案中,是轴对称图形的是( )
A. B. C. D.
2. 如图,∠ABC=∠DCB,要说明△ABC≌△DCB,添加的条件不能是( )
A. AC=DB B. ∠A=∠D
C. BE=CE D. AB=DC
3. 等腰三角形的周长为,其中一边长为,则该等腰三角形的底边为( )
A. 或 B. 或 C. D.
4. 已知等腰三角形的两边长分别为3和4,则该等腰三角形的周长为( )
A. 10 B. 11 C. 10或11 D. 12
5. 下列说法正确的是( )
A. 4的平方根是2 B. 的立方根是
C. 没有平方根 D. 2是4的一个平方根
6. 如图,在和中,,,要使得,还需要补充一个条件,则下列错误条件是( )
A. B. C. D.
7. 如图,在△ABC中,∠B=50°,将△ABC绕点A按逆时针方向旋转得到.若点B′恰好落在BC边上,则 的度数为( )
A. 50° B. 60° C. 80° D. 100°
8. 如图,在正方形中,E是的中点,将沿翻折至,连接,则与互余的角有( )
A. 2个 B. 3个 C. 4个 D. 5个
9. 勾股定理是人类最伟大的科学发现之一,在我国古算书(周髀算经)中早有记载;如图1,以直角三角形的各边为边分别向外作正方形,再把较小的两张正方形纸片按图2的方式放置在最大正方形内若直角三角形两直角边分别为6和8,则图中阴影部分的面积为( )
A. 20 B. 24 C. 28 D. 无法求出
10. 如图,在等腰中,,平分,平分分别为射线上的动点,若,则的最小值为( )
A. 4 B. 6 C. 8 D. 10
二、填空题(本大题共8小题,每空3分,共30分.请把答案填写在答题卡上相应的位置)
11. 如图,在中,.以、为边的正方形的面积分别为、,若,,则的长为______.
12. 如图,小明在C处看西北方向上有一凉亭A,北偏东30°的方向上有一棵大树B,已知凉亭A在大树B的正西方向,若小明距离大树100米,则凉亭与大树之间的距离是__________米.
13. 如图,已知,,与相交于点,若,,则_____.
14. 若等腰三角形腰长为,底边长为,那么它面积为________.
15. 在△ABC中,AB=AC,∠BAC=110°,点D在BC边上,连接AD,若△ABD为直角三角形,则∠ADC的度数为_____.
16. 如图所示,A村、B村都在河边CD的同侧,已知AC=1km,BD=3km,CD=3km.若在河边CD上选点建水厂,则A村、B村到水厂的距离之和的最小值为 ___.
17. 已知中,,,,将它一条直角边沿一锐角角平分线所在直线翻折,使直角顶点落在斜边上点D处,折痕交另一直角边于点E,则折叠后不重合部分三角形的周长为______.
18. 如图,在等腰三角形ACB中,AC=BC=10,AB=16,D为底边AB上一动点(不与点A,B重合),DE⊥AC,DF⊥BC,垂足分别为点E,F,则DE+DF等于_____.
三、解答题(本大题共9小题,共60分)
19. 如图,已知AB=DC,ABCD,E、F是AC上两点,且AF=CE.求证:△ABE≌△CDF.
20. 如图,AB=AC,AC的垂直平分线交AB于D,交AC于E.
(1)若∠A=40°,求∠BCD的度数;
(2)若AE=5,△BCD周长17,求△ABC的周长.
21. 如图,四边形ABCD中,ADBC,E为CD的中点,连结BE并延长交AD的延长线于点F,
(1)求证:△BCE≌△FDE;
(2)连结AE,当AE⊥BF,BC=2,AD=1时,求AB的长.
22. 小明和小亮学习了“勾股定理”之后,为了测量风筝的垂直高度,他们进行了如下操作:①测得水平距离的长为15米;②根据手中剩余线的长度计算出风筝线的长为25米;③牵线放风筝的小明的身高为1.6米.
(1)求风筝的垂直高度;
(2)如果小明想风筝沿方向下降12米,则他应该往回收线多少米?
23. 如图所示,在等腰ABC中,AB=AC,AF为BC的中线,D为AF上的一点,且BD的垂直平分线过点C并交BD于E,求证:BCD是等边三角形.
24. (1)如图1,已知:在ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E. 证明:DE=BD+CE.(提示:由于DE=AD+AE,证明AD=CE,AE=BD即可)
(2)如图2,将(1)中条件改为:在ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=,其中为任意钝角,请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且ABF和ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试证明DEF是等边三角形.
25. 如图1,在中,,动点以每秒的速度从点出发,沿线段向点运动.设点的运动时间为秒.
(知识储备:一个角是的等腰三角形是等边三角形.直角三角形中角所对的边等于斜边的一半.).
(1)当时,求证:是直角三角形.
(2)如图2,若另一动点在线段上以每秒的速度由点向点运动,且与点同时出发,点到达终点时点也随之停止运动.当是直角三角形时,直接写出的值.
(3)如图3,若另一动点从点出发,以每秒的速度沿射线方向运动,且与点同时出发.当点到达终点时点也随之停止运动,连接交于点,过点作于.在运动过程中,线段的长度是否发生变化?为什么?
26. 已知:如图,在中,,,点C、D分别是直线上一个动点.
(1)若是等腰三角形,用直尺和圆规作出点C(不写作法,保留作图痕迹),直接写出的长;
(2)若,求的长;
(3)将沿过中点E的直线翻折,点A落点记为Q,设折痕为,若折叠后长为4,则长为 .(直接写出答案,不需要解答过程)
同课章节目录
