第12章三角形复习检测卷(含答案)2024-2025学年人教版数学八年级上册
文档属性
| 名称 | 第12章三角形复习检测卷(含答案)2024-2025学年人教版数学八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 452.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-06 00:00:00 | ||
图片预览


文档简介
第12章三角形复习检测卷-2024-2025学年数学八年级上册人教版
一.选择题(共8小题)
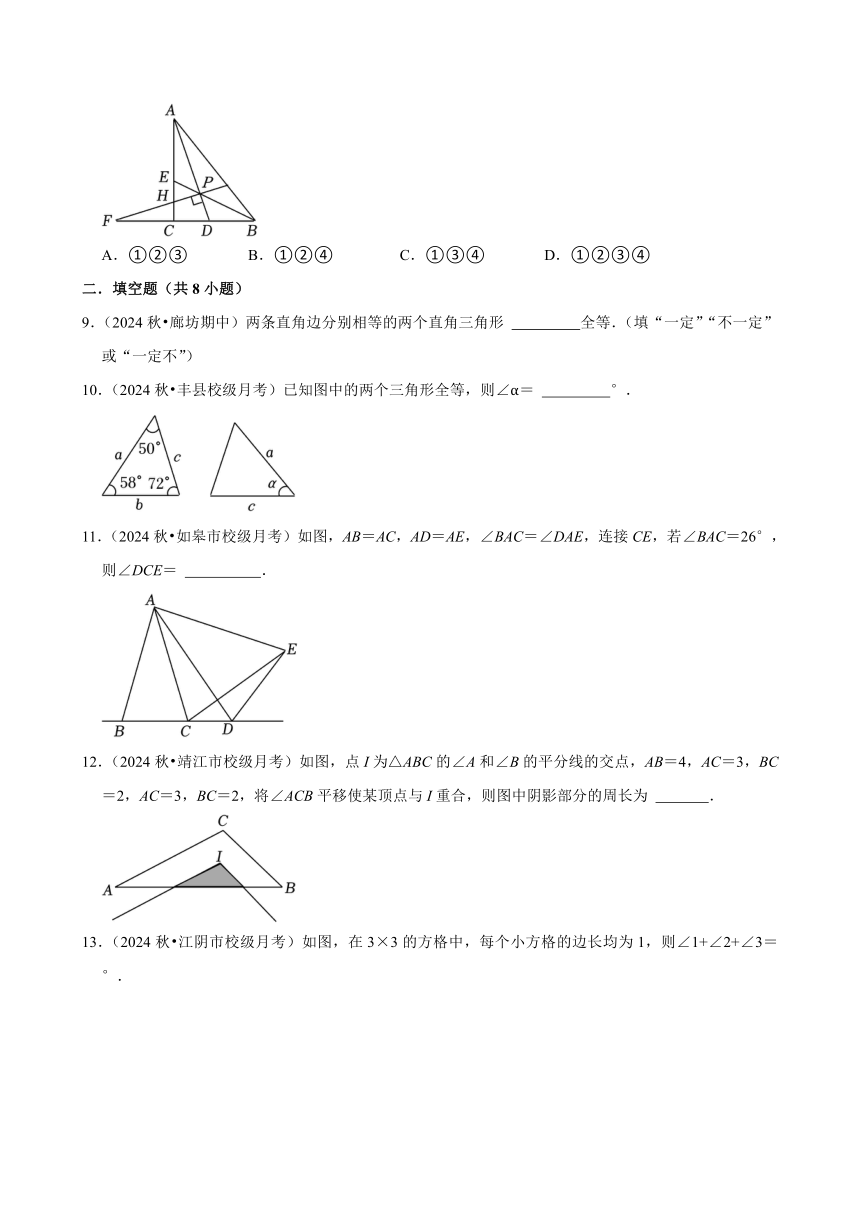
1.(2023秋 硚口区期末)如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形.他的依据是( )
A.SAS B.ASA C.AAS D.SSS
2.(2023秋 南宁期末)如图,若△ABC≌△DEC,∠A=35°,则∠D的度数是( )
A.50° B.45° C.40° D.35°
3.(2023秋 南宁期末)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,若BC=5,BD=3,则点D到AB的距离是( )
A.2 B.3 C.4 D.5
4.(2024秋 双辽市期中)为了测量无法直接测量的池塘两端A,B的距离,小王同学设计了一个测量A,B距离的方案.如图,先确定直线AB,过点B作直线BE⊥AB,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即得AB=BC.根据的原理是( )
A.HL B.ASA C.SAS D.SS
5.(2024秋 凉州区期中)如图所示,AB=AC,AD=AE,点B、D、E在一条直线上,∠BAC=∠DAE,∠1=35°,∠2=60°,则∠3的度数为( )
A.60° B.50° C.35° D.25°
6.(2024秋 良庆区校级月考)如图,已知点P在∠AOB的平分线OC上,PF⊥OA于点F,PE⊥OB于点E,若PE=8,则PF长( )
A.4 B.6 C.8 D.10
7.(2024秋 乐陵市校级月考)如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,当其中一点到达终点时,另一点也随之停止运动.设运动时间为t(s),若存在某一时刻使△ACP与△BPQ全等,则点Q的运动速度为( )
A.0.5cm/s B.1cm/s
C.0.5cm/s或1.5cm/s D.1cm/s或1.5cm/s
8.(2024秋 宜兴市校级月考)如图,在△ABC中,∠ACB=90°,AD、BE为△ABC的角平分线相交于点P,过点P作PF⊥AD交BC延长线于点F,下列四个结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,则CP平分∠ACB.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二.填空题(共8小题)
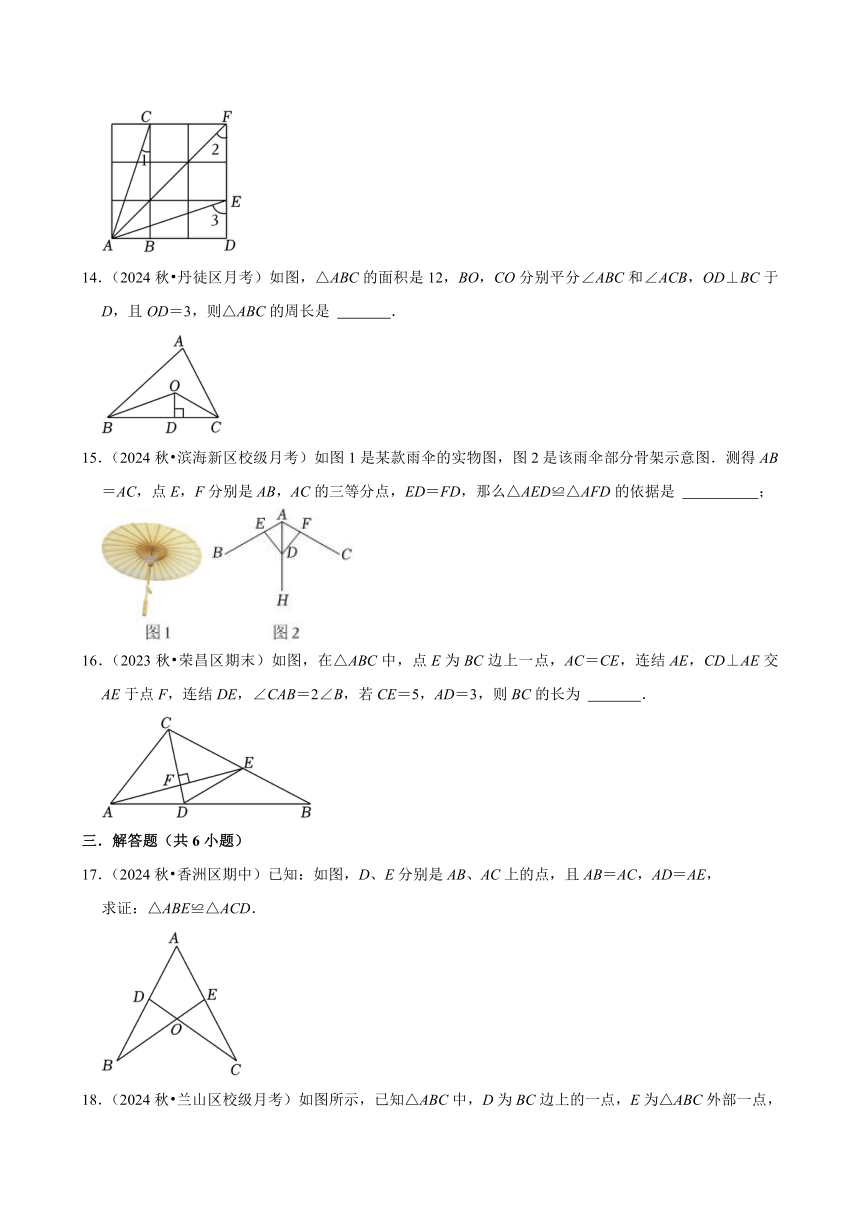
9.(2024秋 廊坊期中)两条直角边分别相等的两个直角三角形 全等.(填“一定”“不一定”或“一定不”)
10.(2024秋 丰县校级月考)已知图中的两个三角形全等,则∠α= °.
11.(2024秋 如皋市校级月考)如图,AB=AC,AD=AE,∠BAC=∠DAE,连接CE,若∠BAC=26°,则∠DCE= .
12.(2024秋 靖江市校级月考)如图,点I为△ABC的∠A和∠B的平分线的交点,AB=4,AC=3,BC=2,AC=3,BC=2,将∠ACB平移使某顶点与I重合,则图中阴影部分的周长为 .
13.(2024秋 江阴市校级月考)如图,在3×3的方格中,每个小方格的边长均为1,则∠1+∠2+∠3= °.
14.(2024秋 丹徒区月考)如图,△ABC的面积是12,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是 .
15.(2024秋 滨海新区校级月考)如图1是某款雨伞的实物图,图2是该雨伞部分骨架示意图.测得AB=AC,点E,F分别是AB,AC的三等分点,ED=FD,那么△AED≌△AFD的依据是 ;
16.(2023秋 荣昌区期末)如图,在△ABC中,点E为BC边上一点,AC=CE,连结AE,CD⊥AE交AE于点F,连结DE,∠CAB=2∠B,若CE=5,AD=3,则BC的长为 .
三.解答题(共6小题)
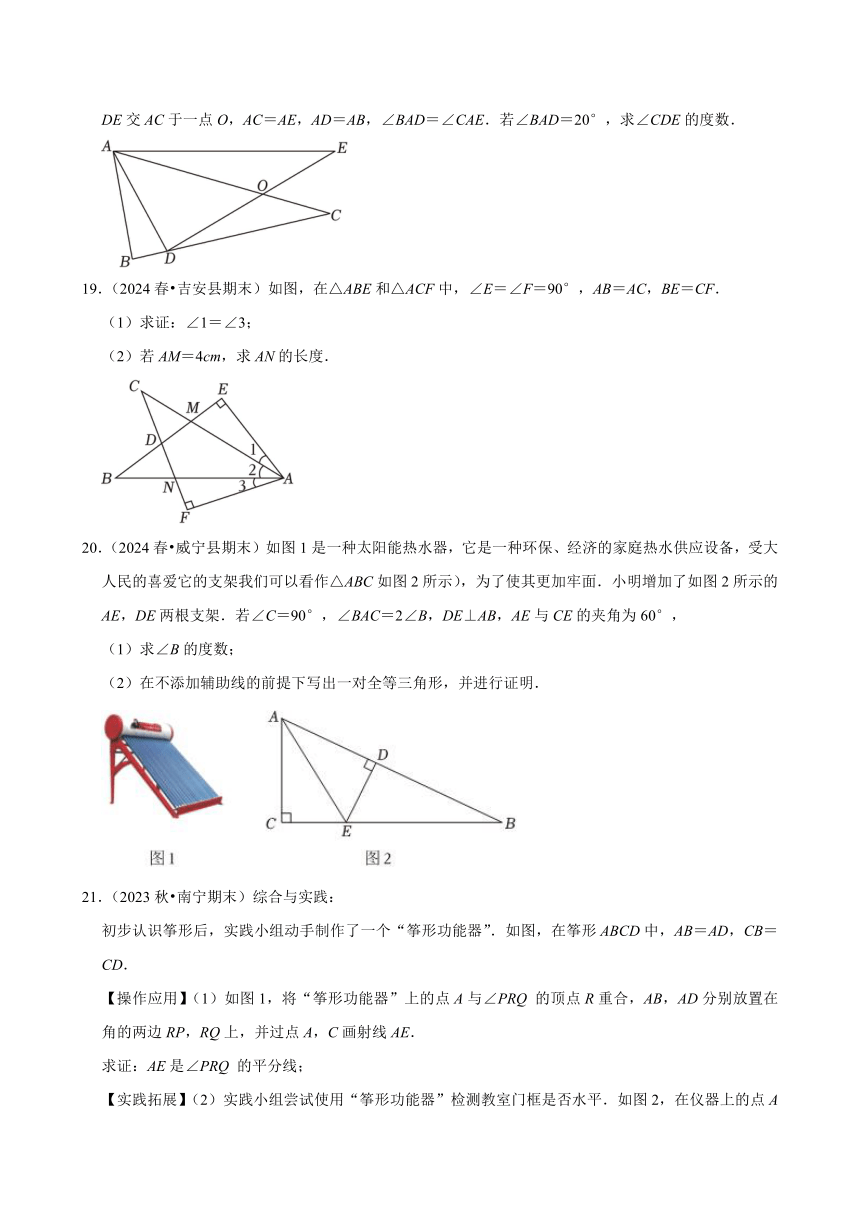
17.(2024秋 香洲区期中)已知:如图,D、E分别是AB、AC上的点,且AB=AC,AD=AE,
求证:△ABE≌△ACD.
18.(2024秋 兰山区校级月考)如图所示,已知△ABC中,D为BC边上的一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAD=∠CAE.若∠BAD=20°,求∠CDE的度数.
19.(2024春 吉安县期末)如图,在△ABE和△ACF中,∠E=∠F=90°,AB=AC,BE=CF.
(1)求证:∠1=∠3;
(2)若AM=4cm,求AN的长度.
20.(2024春 威宁县期末)如图1是一种太阳能热水器,它是一种环保、经济的家庭热水供应设备,受大人民的喜爱它的支架我们可以看作△ABC如图2所示),为了使其更加牢面.小明增加了如图2所示的AE,DE两根支架.若∠C=90°,∠BAC=2∠B,DE⊥AB,AE与CE的夹角为60°,
(1)求∠B的度数;
(2)在不添加辅助线的前提下写出一对全等三角形,并进行证明.
21.(2023秋 南宁期末)综合与实践:
初步认识筝形后,实践小组动手制作了一个“筝形功能器”.如图,在筝形ABCD中,AB=AD,CB=CD.
【操作应用】(1)如图1,将“筝形功能器”上的点A与∠PRQ 的顶点R重合,AB,AD分别放置在角的两边RP,RQ上,并过点A,C画射线AE.
求证:AE是∠PRQ 的平分线;
【实践拓展】(2)实践小组尝试使用“筝形功能器”检测教室门框是否水平.如图2,在仪器上的点A处栓一条线绳,线绳另一端挂一个铅锤,仪器上的点B,D紧贴门框上方,观察发现线绳恰好经过点C,即判断门框是水平的.实践小组的判断对吗?请说明理由.
22.(2024秋 滨海新区校级期中)已知:∠MON=α,点P是∠MON平分线上的一点,点A在射线OM上,作∠APB=180°﹣α,交直线ON于点B,作PC⊥ON于点C.
(1)观察猜想:如图①,当∠MON=90°时,PA和PB的数量关系是 .
(2)探究证明:如图②,当∠MON=60°时,(1)中的结论还成立吗?若成立,请说明理由;若不成立,请直接写出PA,PB之间另外的数量关系.
(3)拓展延伸:如图③,当∠MON=60°,点B在射线ON的反向延长线上时,判断线段OC,OA及BC之间的数量关系,并说明理由.
第12章三角形复习检测卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共8小题)
1.(2023秋 硚口区期末)如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形.他的依据是( )
A.SAS B.ASA C.AAS D.SSS
【解答】解:如图,∠A、AB、∠B都可以测量,
即他的依据是ASA.
故选:B.
2.(2023秋 南宁期末)如图,若△ABC≌△DEC,∠A=35°,则∠D的度数是( )
A.50° B.45° C.40° D.35°
【解答】解:∵△ABC≌△EC,
∴∠D=∠A=35°.
故选:D.
3.(2023秋 南宁期末)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,若BC=5,BD=3,则点D到AB的距离是( )
A.2 B.3 C.4 D.5
【解答】解:如图,过点D作DE⊥AB于点E,
∵BC=5,BD=3,
∴CD=BC﹣BD=5﹣3=2,
∵AD是∠BAC的角平分线,∠C=90°,
∴DE=CD=2,
即点D到AB的距离是2,
故选:A.
4.(2024秋 双辽市期中)为了测量无法直接测量的池塘两端A,B的距离,小王同学设计了一个测量A,B距离的方案.如图,先确定直线AB,过点B作直线BE⊥AB,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即得AB=BC.根据的原理是( )
A.HL B.ASA C.SAS D.SS
【解答】解:由题意得∠DBA=∠DBC=90°,
在Rt△ABD与Rt△CBD中,
,
∴Rt△ABD≌Rt△CBD(HL),
∴AB=BC.
故选:A.
5.(2024秋 凉州区期中)如图所示,AB=AC,AD=AE,点B、D、E在一条直线上,∠BAC=∠DAE,∠1=35°,∠2=60°,则∠3的度数为( )
A.60° B.50° C.35° D.25°
【解答】解:由三角形外角性质可知:∠ABD=60°﹣35°=25°,
∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠1=∠EAC,
∵,
∴△BAD≌△CAE(SAS),
∴∠3=∠ABD=25°,
故选:D.
6.(2024秋 良庆区校级月考)如图,已知点P在∠AOB的平分线OC上,PF⊥OA于点F,PE⊥OB于点E,若PE=8,则PF长( )
A.4 B.6 C.8 D.10
【解答】解:∵OC平分∠AOB,PF⊥OA于点F,PE⊥OB于点E,
∴PF=PE=8,
故选:C.
7.(2024秋 乐陵市校级月考)如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,当其中一点到达终点时,另一点也随之停止运动.设运动时间为t(s),若存在某一时刻使△ACP与△BPQ全等,则点Q的运动速度为( )
A.0.5cm/s B.1cm/s
C.0.5cm/s或1.5cm/s D.1cm/s或1.5cm/s
【解答】解:设点Q的运动速度是x cm/s,
∵点P的运动速度为1cm/s,点Q的运动速度为x cm/s,它们运动的时间为t s,
∴AP=t cm,BQ=xt cm,
∵AB=4cm,
∴BP=(4﹣t)cm,
∠CAB=∠DBA,
当△ACP≌△BPQ时,
∴AP=BQ,AC=BP,
∴,
∴;
当△ACP≌△BQP时,
∴AP=BP,BQ=AC,
∴,
∴.
∴当△ACP与△BPQ全等时,点Q的运动速度为1cm/s或1.5cm/s.
故选:D.
8.(2024秋 宜兴市校级月考)如图,在△ABC中,∠ACB=90°,AD、BE为△ABC的角平分线相交于点P,过点P作PF⊥AD交BC延长线于点F,下列四个结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,则CP平分∠ACB.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【解答】解:∵在△ABC中,∠ACB=90°,
∴∠BAC+∠ABC=90°,
又∵AD、BE分别平分∠BAC、∠ABC,
∴,
∴∠APB=135°,故①正确.
∴∠BPD=45°,
又∵PF⊥AD,
∴∠FPB=90°+45°=135°,
∴∠APB=∠FPB,
在△ABP和△FBP中,
,
∴△ABP≌△FBP(AAS),
∴∠BAP=∠BFP,PA=PF,AB=FB,故②正确.
在△APH和△FPD中,
,
∴△APH≌△FPD(AAS),
∴PH=PD,故③正确.
∵△ABC的角平分线AD、BE相交于点P,
∴点P到AB、AC的距离相等,点P到AB、AC的距离相等,
∴点P到BC、AC的距离相等,
∴点P在∠ACB的平分线上,
∴CP平分∠ACB,故④正确.
综上,正确的有①②③④.
故选:D.
二.填空题(共8小题)
9.(2024秋 廊坊期中)两条直角边分别相等的两个直角三角形 一定 全等.(填“一定”“不一定”或“一定不”)
【解答】解法一:∵两个直角三角形的两条直角边对应相等,而且所夹的角为直角,
∴根据SAS可知这两个直角三角形全等.
解法二:∵两个直角三角形的两条直角边对应相等,
∴两个直角三角形的斜边相等,
∴根据HL可知这两个直角三角形全等.
故答案为:一定.
10.(2024秋 丰县校级月考)已知图中的两个三角形全等,则∠α= 50 °.
【解答】解:∵两个三角形全等,
∴∠α的度数是50°.
故答案为:50.
11.(2024秋 如皋市校级月考)如图,AB=AC,AD=AE,∠BAC=∠DAE,连接CE,若∠BAC=26°,则∠DCE= 26° .
【解答】解:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABD=∠ACE,
又∵AB=AC,∠BAC=26°,
∴∠ABC=∠ACB=∠ACE==77°,
∴∠DCE=180°﹣∠ACB﹣∠ACE=180°﹣2×77°=26°,
故答案为:26°.
12.(2024秋 靖江市校级月考)如图,点I为△ABC的∠A和∠B的平分线的交点,AB=4,AC=3,BC=2,AC=3,BC=2,将∠ACB平移使某顶点与I重合,则图中阴影部分的周长为 4 .
【解答】解:连接AI、BI,
∵点I为△ABC的内心,
∴AI平分∠CAB,
∴∠CAI=∠BAI,
由平移得:AC∥DI,
∴∠CAI=∠AID,
∴∠BAI=∠AID,
∴AD=DI,
同理可得:BE=EI,
∴△DIE的周长=DE+DI+EI=DE+AD+BE=AB=4,
即图中阴影部分的周长为4,
故答案为:4.
13.(2024秋 江阴市校级月考)如图,在3×3的方格中,每个小方格的边长均为1,则∠1+∠2+∠3= 135 °.
【解答】解:由网格可知:AB=ED=1,∠ABC=∠EDA=90°,BC=DA=3,
在△ACB和△EAD中,
,
∴△ACB≌△EAD(SAS),
∴∠1=∠EAD,
∵∠EAD+∠3=90°,
∴∠1+∠3=90°,
∵∠2=45°,
∴∠1+∠2+∠3=135°,
故答案为:135.
14.(2024秋 丹徒区月考)如图,△ABC的面积是12,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是 8 .
【解答】解:作OE⊥AB于E,OF⊥AC于F,连接OA,
∵BO平分∠ABC,OE⊥AB,OD⊥BC,
∴OE=OD=3,
同理可得:OF=OD=3,
∵S△ABC=S△AOB+S△BOC+S△AOC=OD (AB+BC+CA)=(AB+BC+CA)×3=12
∴AB+BC+AC=8,
故答案为:8.
15.(2024秋 滨海新区校级月考)如图1是某款雨伞的实物图,图2是该雨伞部分骨架示意图.测得AB=AC,点E,F分别是AB,AC的三等分点,ED=FD,那么△AED≌△AFD的依据是 SSS ;
【解答】解:∵点E,F分别是AB,AC的三等分点,
∴,
∵AB=AC,
∴AE=AF,
在△AED与△AFD中,
,
∴△AED≌△AFD(SSS),
故答案为:SSS.
16.(2023秋 荣昌区期末)如图,在△ABC中,点E为BC边上一点,AC=CE,连结AE,CD⊥AE交AE于点F,连结DE,∠CAB=2∠B,若CE=5,AD=3,则BC的长为 8 .
【解答】解:∵AC=CE,CD⊥AE.
∴AF=EF,∠AFD=∠EFD=90°.
∠CAE=∠CEA.
在△ADF和△EDF中.
.
∴△ADF≌△EDF(SAS).
∴∠DAF=∠DEF,AD=ED.
∴∠CAB=∠CAE+∠DAF=∠CEA+∠DEF=∠CED.
又∵∠CAB=2∠B.
∠CED=∠B+∠EDB.
∴∠EDB=∠B.
∴ED=EB.
∵AD=3.
∴AD=ED=EB=3.
∵CE=5.
∴BC=BE+CE=3+5=8.
故答案为:8.
三.解答题(共6小题)
17.(2024秋 香洲区期中)已知:如图,D、E分别是AB、AC上的点,且AB=AC,AD=AE,
求证:△ABE≌△ACD.
【解答】证明:在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS).
18.(2024秋 兰山区校级月考)如图所示,已知△ABC中,D为BC边上的一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAD=∠CAE.若∠BAD=20°,求∠CDE的度数.
【解答】解:∵∠BAD=∠CAE,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS),
∴∠C=∠E,
∵∠BAD=20°,
∴∠CAE=∠BAD=20°,
∵∠AOE=∠DOC,∠E=∠C,
∴∠CAE=∠CDE,
∴∠CDE=20°.
19.(2024春 吉安县期末)如图,在△ABE和△ACF中,∠E=∠F=90°,AB=AC,BE=CF.
(1)求证:∠1=∠3;
(2)若AM=4cm,求AN的长度.
【解答】(1)证明:在Rt△ABE和Rt△ACF中,
,
∴Rt△ABE≌Rt△ACF(HL),
∴∠BAE=∠CAF,
∴∠BAE﹣∠2=∠CAF﹣∠2,
∵∠1=∠BAE﹣∠2,∠3=∠CAF﹣∠2,
∴∠1=∠3.
(2)解:由(1)得Rt△ABE≌Rt△ACF,∠1=∠3,
∴AE=AF,
在△AEM和△AFN中,
,
∴△AEM≌△AFN(ASA),
∴AM=AN.
∵AM=4cm,
∴AM=AN=4cm,
∴AN的长度是4cm.
20.(2024春 威宁县期末)如图1是一种太阳能热水器,它是一种环保、经济的家庭热水供应设备,受大人民的喜爱它的支架我们可以看作△ABC如图2所示),为了使其更加牢面.小明增加了如图2所示的AE,DE两根支架.若∠C=90°,∠BAC=2∠B,DE⊥AB,AE与CE的夹角为60°,
(1)求∠B的度数;
(2)在不添加辅助线的前提下写出一对全等三角形,并进行证明.
【解答】解:(1)在Rt△ABC中,∠C=90°,∠BAC=2∠B,
∴2∠B+∠B=90°,
∴∠B=30°;
(2)△ACE≌△ADE,(答案不唯一)证明如下:
在Rt△ACE中,∠C=90°,∠AEC=60°,
∴∠CAE=30°,
由(1)知,∠B=30°,
∴∠BAC=90°﹣30°=60°,
∴∠CAE=∠DAE=30°,
在△ACE与△ADE中,
,
∴△ACE≌△ADE(AAS).
21.(2023秋 南宁期末)综合与实践:
初步认识筝形后,实践小组动手制作了一个“筝形功能器”.如图,在筝形ABCD中,AB=AD,CB=CD.
【操作应用】(1)如图1,将“筝形功能器”上的点A与∠PRQ 的顶点R重合,AB,AD分别放置在角的两边RP,RQ上,并过点A,C画射线AE.
求证:AE是∠PRQ 的平分线;
【实践拓展】(2)实践小组尝试使用“筝形功能器”检测教室门框是否水平.如图2,在仪器上的点A处栓一条线绳,线绳另一端挂一个铅锤,仪器上的点B,D紧贴门框上方,观察发现线绳恰好经过点C,即判断门框是水平的.实践小组的判断对吗?请说明理由.
【解答】(1)证明:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
∴AE是∠PRQ 的平分线;
(2)解:实践小组的判断对,理由如下:
∵△ABD是等腰三角形,AB=AD,
由(1)知:AC平分∠BAD,
∴AC⊥BD,
∵AC是铅锤线,
∴BD是水平的.
∴门框是水平的.
∴实践小组的判断对.
22.(2024秋 滨海新区校级期中)已知:∠MON=α,点P是∠MON平分线上的一点,点A在射线OM上,作∠APB=180°﹣α,交直线ON于点B,作PC⊥ON于点C.
(1)观察猜想:如图①,当∠MON=90°时,PA和PB的数量关系是 AP=BP .
(2)探究证明:如图②,当∠MON=60°时,(1)中的结论还成立吗?若成立,请说明理由;若不成立,请直接写出PA,PB之间另外的数量关系.
(3)拓展延伸:如图③,当∠MON=60°,点B在射线ON的反向延长线上时,判断线段OC,OA及BC之间的数量关系,并说明理由.
【解答】解:(1)作PD⊥OM于点D,如图,
∵点P在∠MON的角平分线上,且PC⊥ON于C,
∴PC=PD,
∵∠MON=90°,∠APB=180°﹣α,
∴∠APB=90°,∠CPD=90°,
∴∠APD+∠BPD=90°,∠BPC+∠BPD=90°,
∴∠APD=∠BPC,
∵∠PDA=∠PCB=90°,
在△APD和△BPC中,
,
∴△APD≌△BPC(ASA),
∴AP=BP;
(2)(1)中的结论还成立,
理由如下:如图2,作PD⊥OM于点D,
∵点P在∠MON的角平分线上,且PC⊥ON于C,
∴PC=PD,
∵∠MON=60°,∠APB=180°﹣α,
∴∠APB=120°,
在四边形OCPD中,∠CPD=360°﹣90°﹣90°﹣60°=120°,
∴∠APD+∠BPD=120°,∠BPC+∠BPD=120°,
∴∠APD=∠BPC,
∵∠PDA=∠PCB=90°,
在△APD和△BPC中,
,
∴△APD≌△BPC(ASA),
∴AP=BP;
(3)OA=BC+OC.
理由如下:如图3,作PD⊥OM于点D,
同(2)可证△APD≌△BPC,
∴AD=BC,
点P在∠MON的角平分线上,且PC⊥ON于C,
∴PC=PD,
在Rt△OPD和Rt△OPC中,
,
∴Rt△OPD≌Rt△OPC(HL),
∴OC=OD,
∴OA﹣AD=OD=OC,
∴OA﹣BC=OC,
则OA=BC+OC;
一.选择题(共8小题)
1.(2023秋 硚口区期末)如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形.他的依据是( )
A.SAS B.ASA C.AAS D.SSS
2.(2023秋 南宁期末)如图,若△ABC≌△DEC,∠A=35°,则∠D的度数是( )
A.50° B.45° C.40° D.35°
3.(2023秋 南宁期末)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,若BC=5,BD=3,则点D到AB的距离是( )
A.2 B.3 C.4 D.5
4.(2024秋 双辽市期中)为了测量无法直接测量的池塘两端A,B的距离,小王同学设计了一个测量A,B距离的方案.如图,先确定直线AB,过点B作直线BE⊥AB,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即得AB=BC.根据的原理是( )
A.HL B.ASA C.SAS D.SS
5.(2024秋 凉州区期中)如图所示,AB=AC,AD=AE,点B、D、E在一条直线上,∠BAC=∠DAE,∠1=35°,∠2=60°,则∠3的度数为( )
A.60° B.50° C.35° D.25°
6.(2024秋 良庆区校级月考)如图,已知点P在∠AOB的平分线OC上,PF⊥OA于点F,PE⊥OB于点E,若PE=8,则PF长( )
A.4 B.6 C.8 D.10
7.(2024秋 乐陵市校级月考)如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,当其中一点到达终点时,另一点也随之停止运动.设运动时间为t(s),若存在某一时刻使△ACP与△BPQ全等,则点Q的运动速度为( )
A.0.5cm/s B.1cm/s
C.0.5cm/s或1.5cm/s D.1cm/s或1.5cm/s
8.(2024秋 宜兴市校级月考)如图,在△ABC中,∠ACB=90°,AD、BE为△ABC的角平分线相交于点P,过点P作PF⊥AD交BC延长线于点F,下列四个结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,则CP平分∠ACB.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
二.填空题(共8小题)
9.(2024秋 廊坊期中)两条直角边分别相等的两个直角三角形 全等.(填“一定”“不一定”或“一定不”)
10.(2024秋 丰县校级月考)已知图中的两个三角形全等,则∠α= °.
11.(2024秋 如皋市校级月考)如图,AB=AC,AD=AE,∠BAC=∠DAE,连接CE,若∠BAC=26°,则∠DCE= .
12.(2024秋 靖江市校级月考)如图,点I为△ABC的∠A和∠B的平分线的交点,AB=4,AC=3,BC=2,AC=3,BC=2,将∠ACB平移使某顶点与I重合,则图中阴影部分的周长为 .
13.(2024秋 江阴市校级月考)如图,在3×3的方格中,每个小方格的边长均为1,则∠1+∠2+∠3= °.
14.(2024秋 丹徒区月考)如图,△ABC的面积是12,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是 .
15.(2024秋 滨海新区校级月考)如图1是某款雨伞的实物图,图2是该雨伞部分骨架示意图.测得AB=AC,点E,F分别是AB,AC的三等分点,ED=FD,那么△AED≌△AFD的依据是 ;
16.(2023秋 荣昌区期末)如图,在△ABC中,点E为BC边上一点,AC=CE,连结AE,CD⊥AE交AE于点F,连结DE,∠CAB=2∠B,若CE=5,AD=3,则BC的长为 .
三.解答题(共6小题)
17.(2024秋 香洲区期中)已知:如图,D、E分别是AB、AC上的点,且AB=AC,AD=AE,
求证:△ABE≌△ACD.
18.(2024秋 兰山区校级月考)如图所示,已知△ABC中,D为BC边上的一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAD=∠CAE.若∠BAD=20°,求∠CDE的度数.
19.(2024春 吉安县期末)如图,在△ABE和△ACF中,∠E=∠F=90°,AB=AC,BE=CF.
(1)求证:∠1=∠3;
(2)若AM=4cm,求AN的长度.
20.(2024春 威宁县期末)如图1是一种太阳能热水器,它是一种环保、经济的家庭热水供应设备,受大人民的喜爱它的支架我们可以看作△ABC如图2所示),为了使其更加牢面.小明增加了如图2所示的AE,DE两根支架.若∠C=90°,∠BAC=2∠B,DE⊥AB,AE与CE的夹角为60°,
(1)求∠B的度数;
(2)在不添加辅助线的前提下写出一对全等三角形,并进行证明.
21.(2023秋 南宁期末)综合与实践:
初步认识筝形后,实践小组动手制作了一个“筝形功能器”.如图,在筝形ABCD中,AB=AD,CB=CD.
【操作应用】(1)如图1,将“筝形功能器”上的点A与∠PRQ 的顶点R重合,AB,AD分别放置在角的两边RP,RQ上,并过点A,C画射线AE.
求证:AE是∠PRQ 的平分线;
【实践拓展】(2)实践小组尝试使用“筝形功能器”检测教室门框是否水平.如图2,在仪器上的点A处栓一条线绳,线绳另一端挂一个铅锤,仪器上的点B,D紧贴门框上方,观察发现线绳恰好经过点C,即判断门框是水平的.实践小组的判断对吗?请说明理由.
22.(2024秋 滨海新区校级期中)已知:∠MON=α,点P是∠MON平分线上的一点,点A在射线OM上,作∠APB=180°﹣α,交直线ON于点B,作PC⊥ON于点C.
(1)观察猜想:如图①,当∠MON=90°时,PA和PB的数量关系是 .
(2)探究证明:如图②,当∠MON=60°时,(1)中的结论还成立吗?若成立,请说明理由;若不成立,请直接写出PA,PB之间另外的数量关系.
(3)拓展延伸:如图③,当∠MON=60°,点B在射线ON的反向延长线上时,判断线段OC,OA及BC之间的数量关系,并说明理由.
第12章三角形复习检测卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共8小题)
1.(2023秋 硚口区期末)如图,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形.他的依据是( )
A.SAS B.ASA C.AAS D.SSS
【解答】解:如图,∠A、AB、∠B都可以测量,
即他的依据是ASA.
故选:B.
2.(2023秋 南宁期末)如图,若△ABC≌△DEC,∠A=35°,则∠D的度数是( )
A.50° B.45° C.40° D.35°
【解答】解:∵△ABC≌△EC,
∴∠D=∠A=35°.
故选:D.
3.(2023秋 南宁期末)如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,若BC=5,BD=3,则点D到AB的距离是( )
A.2 B.3 C.4 D.5
【解答】解:如图,过点D作DE⊥AB于点E,
∵BC=5,BD=3,
∴CD=BC﹣BD=5﹣3=2,
∵AD是∠BAC的角平分线,∠C=90°,
∴DE=CD=2,
即点D到AB的距离是2,
故选:A.
4.(2024秋 双辽市期中)为了测量无法直接测量的池塘两端A,B的距离,小王同学设计了一个测量A,B距离的方案.如图,先确定直线AB,过点B作直线BE⊥AB,在直线BE上找可以直接到达点A的一点D,连接DA,作DC=DA,交直线AB于点C,最后测量BC的长即得AB=BC.根据的原理是( )
A.HL B.ASA C.SAS D.SS
【解答】解:由题意得∠DBA=∠DBC=90°,
在Rt△ABD与Rt△CBD中,
,
∴Rt△ABD≌Rt△CBD(HL),
∴AB=BC.
故选:A.
5.(2024秋 凉州区期中)如图所示,AB=AC,AD=AE,点B、D、E在一条直线上,∠BAC=∠DAE,∠1=35°,∠2=60°,则∠3的度数为( )
A.60° B.50° C.35° D.25°
【解答】解:由三角形外角性质可知:∠ABD=60°﹣35°=25°,
∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠1=∠EAC,
∵,
∴△BAD≌△CAE(SAS),
∴∠3=∠ABD=25°,
故选:D.
6.(2024秋 良庆区校级月考)如图,已知点P在∠AOB的平分线OC上,PF⊥OA于点F,PE⊥OB于点E,若PE=8,则PF长( )
A.4 B.6 C.8 D.10
【解答】解:∵OC平分∠AOB,PF⊥OA于点F,PE⊥OB于点E,
∴PF=PE=8,
故选:C.
7.(2024秋 乐陵市校级月考)如图,AB=4cm,AC=BD=3cm,∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,当其中一点到达终点时,另一点也随之停止运动.设运动时间为t(s),若存在某一时刻使△ACP与△BPQ全等,则点Q的运动速度为( )
A.0.5cm/s B.1cm/s
C.0.5cm/s或1.5cm/s D.1cm/s或1.5cm/s
【解答】解:设点Q的运动速度是x cm/s,
∵点P的运动速度为1cm/s,点Q的运动速度为x cm/s,它们运动的时间为t s,
∴AP=t cm,BQ=xt cm,
∵AB=4cm,
∴BP=(4﹣t)cm,
∠CAB=∠DBA,
当△ACP≌△BPQ时,
∴AP=BQ,AC=BP,
∴,
∴;
当△ACP≌△BQP时,
∴AP=BP,BQ=AC,
∴,
∴.
∴当△ACP与△BPQ全等时,点Q的运动速度为1cm/s或1.5cm/s.
故选:D.
8.(2024秋 宜兴市校级月考)如图,在△ABC中,∠ACB=90°,AD、BE为△ABC的角平分线相交于点P,过点P作PF⊥AD交BC延长线于点F,下列四个结论:①∠APB=135°;②BF=BA;③PH=PD;④连接CP,则CP平分∠ACB.其中正确的是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【解答】解:∵在△ABC中,∠ACB=90°,
∴∠BAC+∠ABC=90°,
又∵AD、BE分别平分∠BAC、∠ABC,
∴,
∴∠APB=135°,故①正确.
∴∠BPD=45°,
又∵PF⊥AD,
∴∠FPB=90°+45°=135°,
∴∠APB=∠FPB,
在△ABP和△FBP中,
,
∴△ABP≌△FBP(AAS),
∴∠BAP=∠BFP,PA=PF,AB=FB,故②正确.
在△APH和△FPD中,
,
∴△APH≌△FPD(AAS),
∴PH=PD,故③正确.
∵△ABC的角平分线AD、BE相交于点P,
∴点P到AB、AC的距离相等,点P到AB、AC的距离相等,
∴点P到BC、AC的距离相等,
∴点P在∠ACB的平分线上,
∴CP平分∠ACB,故④正确.
综上,正确的有①②③④.
故选:D.
二.填空题(共8小题)
9.(2024秋 廊坊期中)两条直角边分别相等的两个直角三角形 一定 全等.(填“一定”“不一定”或“一定不”)
【解答】解法一:∵两个直角三角形的两条直角边对应相等,而且所夹的角为直角,
∴根据SAS可知这两个直角三角形全等.
解法二:∵两个直角三角形的两条直角边对应相等,
∴两个直角三角形的斜边相等,
∴根据HL可知这两个直角三角形全等.
故答案为:一定.
10.(2024秋 丰县校级月考)已知图中的两个三角形全等,则∠α= 50 °.
【解答】解:∵两个三角形全等,
∴∠α的度数是50°.
故答案为:50.
11.(2024秋 如皋市校级月考)如图,AB=AC,AD=AE,∠BAC=∠DAE,连接CE,若∠BAC=26°,则∠DCE= 26° .
【解答】解:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△BAD与△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠ABD=∠ACE,
又∵AB=AC,∠BAC=26°,
∴∠ABC=∠ACB=∠ACE==77°,
∴∠DCE=180°﹣∠ACB﹣∠ACE=180°﹣2×77°=26°,
故答案为:26°.
12.(2024秋 靖江市校级月考)如图,点I为△ABC的∠A和∠B的平分线的交点,AB=4,AC=3,BC=2,AC=3,BC=2,将∠ACB平移使某顶点与I重合,则图中阴影部分的周长为 4 .
【解答】解:连接AI、BI,
∵点I为△ABC的内心,
∴AI平分∠CAB,
∴∠CAI=∠BAI,
由平移得:AC∥DI,
∴∠CAI=∠AID,
∴∠BAI=∠AID,
∴AD=DI,
同理可得:BE=EI,
∴△DIE的周长=DE+DI+EI=DE+AD+BE=AB=4,
即图中阴影部分的周长为4,
故答案为:4.
13.(2024秋 江阴市校级月考)如图,在3×3的方格中,每个小方格的边长均为1,则∠1+∠2+∠3= 135 °.
【解答】解:由网格可知:AB=ED=1,∠ABC=∠EDA=90°,BC=DA=3,
在△ACB和△EAD中,
,
∴△ACB≌△EAD(SAS),
∴∠1=∠EAD,
∵∠EAD+∠3=90°,
∴∠1+∠3=90°,
∵∠2=45°,
∴∠1+∠2+∠3=135°,
故答案为:135.
14.(2024秋 丹徒区月考)如图,△ABC的面积是12,BO,CO分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=3,则△ABC的周长是 8 .
【解答】解:作OE⊥AB于E,OF⊥AC于F,连接OA,
∵BO平分∠ABC,OE⊥AB,OD⊥BC,
∴OE=OD=3,
同理可得:OF=OD=3,
∵S△ABC=S△AOB+S△BOC+S△AOC=OD (AB+BC+CA)=(AB+BC+CA)×3=12
∴AB+BC+AC=8,
故答案为:8.
15.(2024秋 滨海新区校级月考)如图1是某款雨伞的实物图,图2是该雨伞部分骨架示意图.测得AB=AC,点E,F分别是AB,AC的三等分点,ED=FD,那么△AED≌△AFD的依据是 SSS ;
【解答】解:∵点E,F分别是AB,AC的三等分点,
∴,
∵AB=AC,
∴AE=AF,
在△AED与△AFD中,
,
∴△AED≌△AFD(SSS),
故答案为:SSS.
16.(2023秋 荣昌区期末)如图,在△ABC中,点E为BC边上一点,AC=CE,连结AE,CD⊥AE交AE于点F,连结DE,∠CAB=2∠B,若CE=5,AD=3,则BC的长为 8 .
【解答】解:∵AC=CE,CD⊥AE.
∴AF=EF,∠AFD=∠EFD=90°.
∠CAE=∠CEA.
在△ADF和△EDF中.
.
∴△ADF≌△EDF(SAS).
∴∠DAF=∠DEF,AD=ED.
∴∠CAB=∠CAE+∠DAF=∠CEA+∠DEF=∠CED.
又∵∠CAB=2∠B.
∠CED=∠B+∠EDB.
∴∠EDB=∠B.
∴ED=EB.
∵AD=3.
∴AD=ED=EB=3.
∵CE=5.
∴BC=BE+CE=3+5=8.
故答案为:8.
三.解答题(共6小题)
17.(2024秋 香洲区期中)已知:如图,D、E分别是AB、AC上的点,且AB=AC,AD=AE,
求证:△ABE≌△ACD.
【解答】证明:在△ABE和△ACD中,
,
∴△ABE≌△ACD(SAS).
18.(2024秋 兰山区校级月考)如图所示,已知△ABC中,D为BC边上的一点,E为△ABC外部一点,DE交AC于一点O,AC=AE,AD=AB,∠BAD=∠CAE.若∠BAD=20°,求∠CDE的度数.
【解答】解:∵∠BAD=∠CAE,
∴∠BAC=∠DAE,
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS),
∴∠C=∠E,
∵∠BAD=20°,
∴∠CAE=∠BAD=20°,
∵∠AOE=∠DOC,∠E=∠C,
∴∠CAE=∠CDE,
∴∠CDE=20°.
19.(2024春 吉安县期末)如图,在△ABE和△ACF中,∠E=∠F=90°,AB=AC,BE=CF.
(1)求证:∠1=∠3;
(2)若AM=4cm,求AN的长度.
【解答】(1)证明:在Rt△ABE和Rt△ACF中,
,
∴Rt△ABE≌Rt△ACF(HL),
∴∠BAE=∠CAF,
∴∠BAE﹣∠2=∠CAF﹣∠2,
∵∠1=∠BAE﹣∠2,∠3=∠CAF﹣∠2,
∴∠1=∠3.
(2)解:由(1)得Rt△ABE≌Rt△ACF,∠1=∠3,
∴AE=AF,
在△AEM和△AFN中,
,
∴△AEM≌△AFN(ASA),
∴AM=AN.
∵AM=4cm,
∴AM=AN=4cm,
∴AN的长度是4cm.
20.(2024春 威宁县期末)如图1是一种太阳能热水器,它是一种环保、经济的家庭热水供应设备,受大人民的喜爱它的支架我们可以看作△ABC如图2所示),为了使其更加牢面.小明增加了如图2所示的AE,DE两根支架.若∠C=90°,∠BAC=2∠B,DE⊥AB,AE与CE的夹角为60°,
(1)求∠B的度数;
(2)在不添加辅助线的前提下写出一对全等三角形,并进行证明.
【解答】解:(1)在Rt△ABC中,∠C=90°,∠BAC=2∠B,
∴2∠B+∠B=90°,
∴∠B=30°;
(2)△ACE≌△ADE,(答案不唯一)证明如下:
在Rt△ACE中,∠C=90°,∠AEC=60°,
∴∠CAE=30°,
由(1)知,∠B=30°,
∴∠BAC=90°﹣30°=60°,
∴∠CAE=∠DAE=30°,
在△ACE与△ADE中,
,
∴△ACE≌△ADE(AAS).
21.(2023秋 南宁期末)综合与实践:
初步认识筝形后,实践小组动手制作了一个“筝形功能器”.如图,在筝形ABCD中,AB=AD,CB=CD.
【操作应用】(1)如图1,将“筝形功能器”上的点A与∠PRQ 的顶点R重合,AB,AD分别放置在角的两边RP,RQ上,并过点A,C画射线AE.
求证:AE是∠PRQ 的平分线;
【实践拓展】(2)实践小组尝试使用“筝形功能器”检测教室门框是否水平.如图2,在仪器上的点A处栓一条线绳,线绳另一端挂一个铅锤,仪器上的点B,D紧贴门框上方,观察发现线绳恰好经过点C,即判断门框是水平的.实践小组的判断对吗?请说明理由.
【解答】(1)证明:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
∴AE是∠PRQ 的平分线;
(2)解:实践小组的判断对,理由如下:
∵△ABD是等腰三角形,AB=AD,
由(1)知:AC平分∠BAD,
∴AC⊥BD,
∵AC是铅锤线,
∴BD是水平的.
∴门框是水平的.
∴实践小组的判断对.
22.(2024秋 滨海新区校级期中)已知:∠MON=α,点P是∠MON平分线上的一点,点A在射线OM上,作∠APB=180°﹣α,交直线ON于点B,作PC⊥ON于点C.
(1)观察猜想:如图①,当∠MON=90°时,PA和PB的数量关系是 AP=BP .
(2)探究证明:如图②,当∠MON=60°时,(1)中的结论还成立吗?若成立,请说明理由;若不成立,请直接写出PA,PB之间另外的数量关系.
(3)拓展延伸:如图③,当∠MON=60°,点B在射线ON的反向延长线上时,判断线段OC,OA及BC之间的数量关系,并说明理由.
【解答】解:(1)作PD⊥OM于点D,如图,
∵点P在∠MON的角平分线上,且PC⊥ON于C,
∴PC=PD,
∵∠MON=90°,∠APB=180°﹣α,
∴∠APB=90°,∠CPD=90°,
∴∠APD+∠BPD=90°,∠BPC+∠BPD=90°,
∴∠APD=∠BPC,
∵∠PDA=∠PCB=90°,
在△APD和△BPC中,
,
∴△APD≌△BPC(ASA),
∴AP=BP;
(2)(1)中的结论还成立,
理由如下:如图2,作PD⊥OM于点D,
∵点P在∠MON的角平分线上,且PC⊥ON于C,
∴PC=PD,
∵∠MON=60°,∠APB=180°﹣α,
∴∠APB=120°,
在四边形OCPD中,∠CPD=360°﹣90°﹣90°﹣60°=120°,
∴∠APD+∠BPD=120°,∠BPC+∠BPD=120°,
∴∠APD=∠BPC,
∵∠PDA=∠PCB=90°,
在△APD和△BPC中,
,
∴△APD≌△BPC(ASA),
∴AP=BP;
(3)OA=BC+OC.
理由如下:如图3,作PD⊥OM于点D,
同(2)可证△APD≌△BPC,
∴AD=BC,
点P在∠MON的角平分线上,且PC⊥ON于C,
∴PC=PD,
在Rt△OPD和Rt△OPC中,
,
∴Rt△OPD≌Rt△OPC(HL),
∴OC=OD,
∴OA﹣AD=OD=OC,
∴OA﹣BC=OC,
则OA=BC+OC;
