第13章轴对称 复习检测卷(含答案)2024-2025学年人教版数学八年级上册
文档属性
| 名称 | 第13章轴对称 复习检测卷(含答案)2024-2025学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 650.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-06 10:43:22 | ||
图片预览



文档简介
第13章轴对称复习检测卷-2024-2025学年数学八年级上册人教版
一.选择题(共8小题)
1.(2024 滨州)数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是( )
A. B.
C. D.
2.(2024 成都模拟)在平面直角坐标系中,点A(3,﹣2),B(m,n)关于x轴对称,将点B向左平移3个单位长度得到点C,则点C的坐标为( )
A.(3,﹣2) B.(3,2) C.(0,﹣2) D.(0,2)
3.(2024秋 宜兴市校级月考)下列说法:①形状相同的两个三角形是全等三角形;②全等三角形的中线相等;③成轴对称的两个图形中,对应点的连线段被对称轴垂直平分;④两条直角边对应相等的两个直角三角形全等.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
4.(2024秋 凉州区校级期中)如图,在△ABC中,AB=AC,且点D为BC上一点,CD=AD,AB=BD,则∠C为( )
A.30° B.36° C.40° D.45°
5.(2024秋 南岗区校级月考)如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=AK,BN=BK,若∠MKN=44°,则∠P=( )
A.90° B.92° C.96° D.98°
6.(2023秋 凤山县期末)如图,OC=CD=DE,若∠BDE=75°,则∠CDE的度数是( )
A.70° B.75° C.80° D.85°
7.(2024春 顺河区期末)如图,在四边形ABCD中,∠C=40°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
A.100° B.90° C.70° D.80°
8.(2024秋 玄武区校级月考)如图,∠ABC=∠ACB,BD、CD分别平分△ABC的内角∠ABC,外角∠ACF,连接AD.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADB+∠ACD=90°;④△ABD和△ACD都是等腰三角形.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题)
9.(2024春 城关区校级期末)如图,已知AB=CB,要使四边形ABCD成为一个轴对称图形,还需添加一个条件,你添加的条件是 .(只需写一个,不添加辅助线)
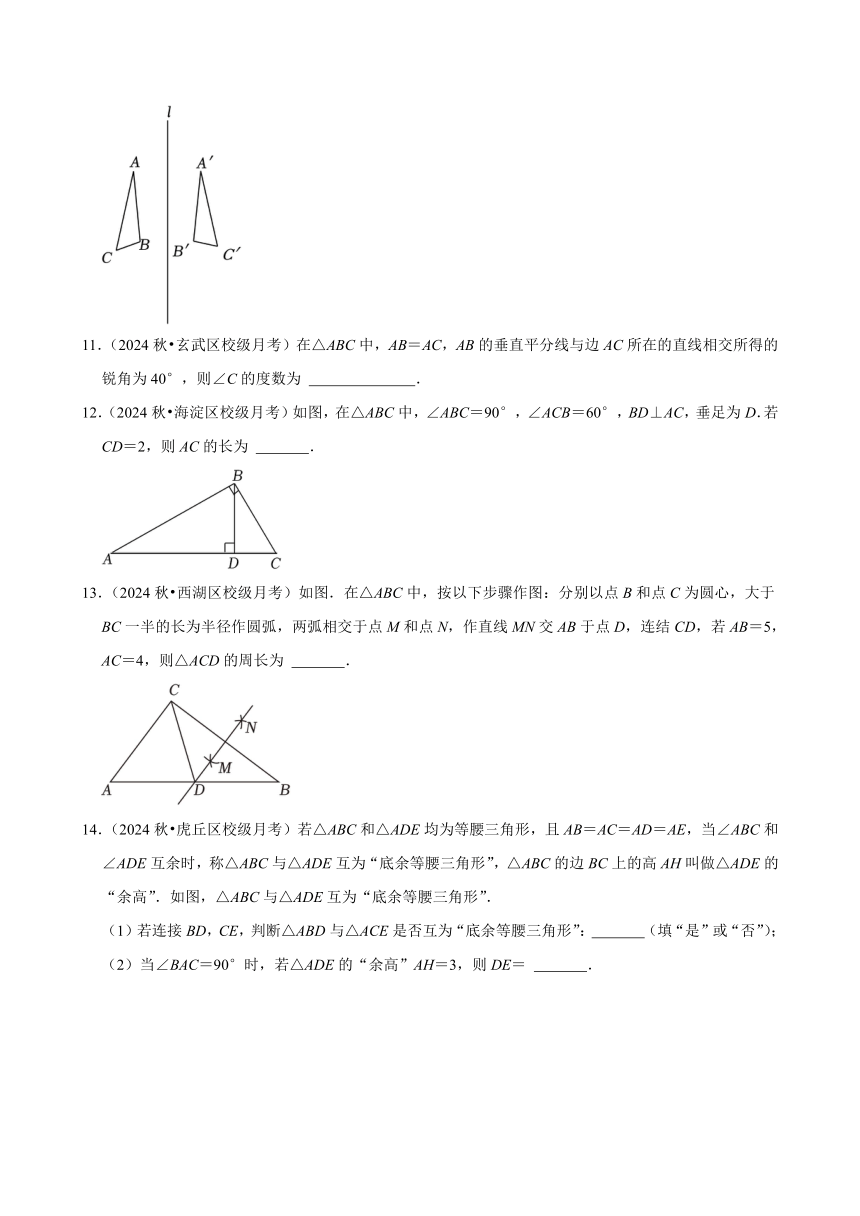
10.(2024秋 六合区校级月考)如图,∠A=30°,∠C'=60°,△ABC与△A'B'C'关于直线l对称,则∠B= .
11.(2024秋 玄武区校级月考)在△ABC中,AB=AC,AB的垂直平分线与边AC所在的直线相交所得的锐角为40°,则∠C的度数为 .
12.(2024秋 海淀区校级月考)如图,在△ABC中,∠ABC=90°,∠ACB=60°,BD⊥AC,垂足为D.若CD=2,则AC的长为 .
13.(2024秋 西湖区校级月考)如图.在△ABC中,按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,作直线MN交AB于点D,连结CD,若AB=5,AC=4,则△ACD的周长为 .
14.(2024秋 虎丘区校级月考)若△ABC和△ADE均为等腰三角形,且AB=AC=AD=AE,当∠ABC和∠ADE互余时,称△ABC与△ADE互为“底余等腰三角形”,△ABC的边BC上的高AH叫做△ADE的“余高”.如图,△ABC与△ADE互为“底余等腰三角形”.
(1)若连接BD,CE,判断△ABD与△ACE是否互为“底余等腰三角形”: (填“是”或“否”);
(2)当∠BAC=90°时,若△ADE的“余高”AH=3,则DE= .
15.(2024秋 姑苏区校级月考)如图,点B,F,D在射线AM上,点G,C,E在射线AN上,且AB=BC=CD=DE=EF=FG=GA,则∠A= °.
16.(2024 武威三模)如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为 .
三.解答题(共7小题)
17.(2023秋 宝丰县期末)平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(3,4),C(3,﹣1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标.
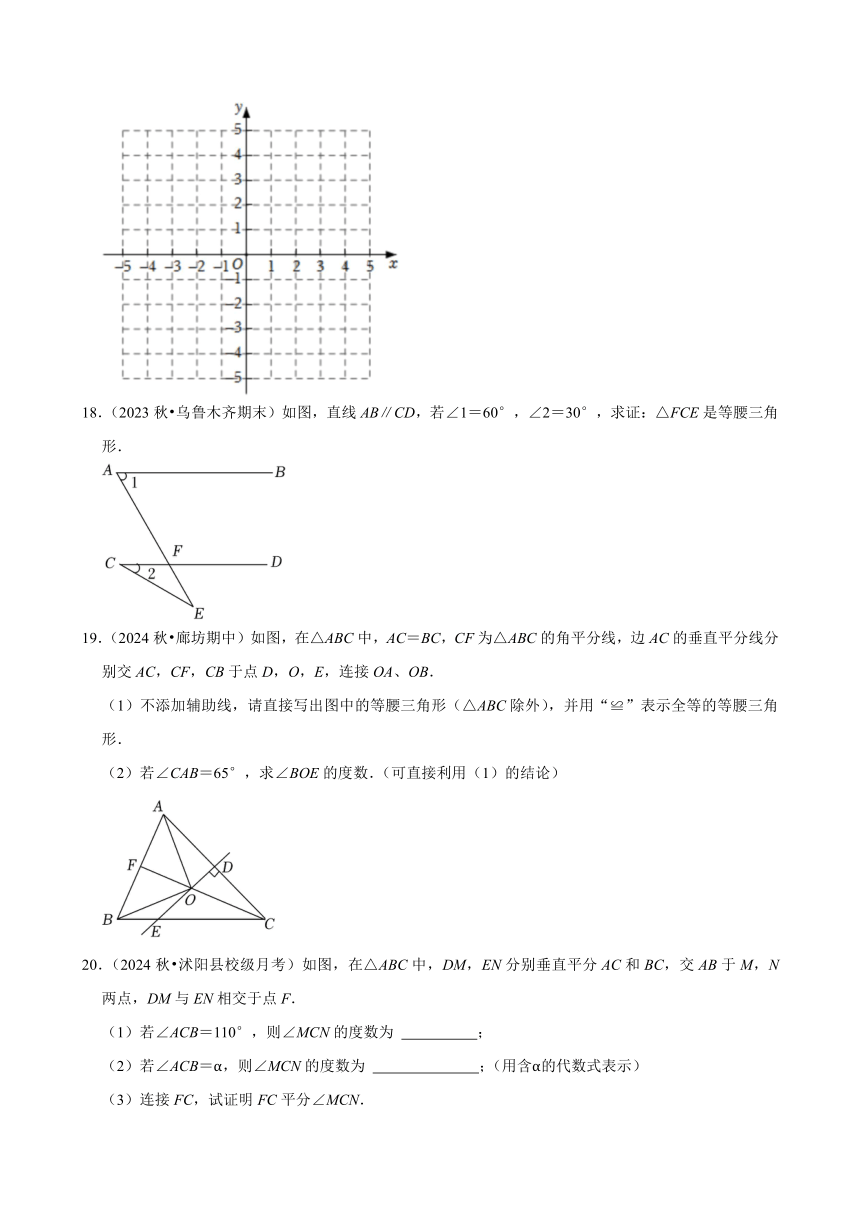
18.(2023秋 乌鲁木齐期末)如图,直线AB∥CD,若∠1=60°,∠2=30°,求证:△FCE是等腰三角形.
19.(2024秋 廊坊期中)如图,在△ABC中,AC=BC,CF为△ABC的角平分线,边AC的垂直平分线分别交AC,CF,CB于点D,O,E,连接OA、OB.
(1)不添加辅助线,请直接写出图中的等腰三角形(△ABC除外),并用“≌”表示全等的等腰三角形.
(2)若∠CAB=65°,求∠BOE的度数.(可直接利用(1)的结论)
20.(2024秋 沭阳县校级月考)如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)若∠ACB=110°,则∠MCN的度数为 ;
(2)若∠ACB=α,则∠MCN的度数为 ;(用含α的代数式表示)
(3)连接FC,试证明FC平分∠MCN.
21.(2024秋 靖江市校级月考)如图,已知AB∥CD,∠BAC的角平分线与CD交于点E,F为射线AB上的一个动点,连接EF,过点C作CG⊥EF,且FG=EG.
(1)已知∠BAC=70°,求∠AEF的度数.
(2)若∠AEF=α,求∠ECG的度数.
22.(2024秋 高州市校级月考)如图1,A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.
现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选方案1:水厂建在C点,修自来水管道到A村,再到B村(即AC+AB).(如图2)方案2:作A点关于直线CD的对称点A',连接A'B交CD于M点,水厂建在M点处,分别向两村修管道AM和BM.(即AM+BM)(如图3)从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工,请利用已有条件分别进行计算,判断哪种方案更合适.
23.(2024秋 高新区月考)如图1,已知A,B为直线MN同侧的两点,连接AP,BP,若∠APM=∠BPN,则称点P为点A,B关于直线MN的“等角点”.
【理解运用】
(1)如图2,在△ABC中,D为BC上一点,点D、E关于直线AB对称,连接EB并延长至点F,判断点B是否为点D、F关于直线AB的“等角点”,并说明理由;
【拓展提升】
(2)如图3,在△ABC中,∠ABC,∠BAC的平分线交于点O,点O到AC的距离为2,直线l垂直平分边BC,点P为O,B关于直线l“等角点”,连接OP,BP,当∠ACB=60°时,OP+BP的值为 .
第13章轴对称复习检测卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共8小题)
1.(2024 滨州)数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是( )
A. B.
C. D.
【解答】解:A、是轴对称图形;
B、不是轴对称图形;
C、是轴对称图形;
D、是轴对称图形;
故选:B.
2.(2024 成都模拟)在平面直角坐标系中,点A(3,﹣2),B(m,n)关于x轴对称,将点B向左平移3个单位长度得到点C,则点C的坐标为( )
A.(3,﹣2) B.(3,2) C.(0,﹣2) D.(0,2)
【解答】解:∵点A(3,﹣2),B(m,n)关于x轴对称,
∴点B的坐标为(3,2),
∴将点B向左平移3个单位长度得到点C,则点C的坐标为(0,2).
故选:D.
3.(2024秋 宜兴市校级月考)下列说法:①形状相同的两个三角形是全等三角形;②全等三角形的中线相等;③成轴对称的两个图形中,对应点的连线段被对称轴垂直平分;④两条直角边对应相等的两个直角三角形全等.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①形状相同的两个三角形是相似三角形,不一定是全等三角形,只有形状相同,大小也相等的两个三角形才是全等三角形,不符合题意;
②全等三角形对应边上的中线相等,不符合题意;
③成轴对称的两个图形中,对应点的连线段被对称轴垂直平分,符合题意;
④两个直角三角形的两条直角边对应相等,这两个直角三角形全等,符合全等三角形的判定定理“SAS”,符合题意.
综上所述,正确的说法有③④共2个.
故选:B.
4.(2024秋 凉州区校级期中)如图,在△ABC中,AB=AC,且点D为BC上一点,CD=AD,AB=BD,则∠C为( )
A.30° B.36° C.40° D.45°
【解答】解:∵AB=AC,CD=AD,AB=BD,
∴∠B=∠C=∠CAD,∠ADB=∠BAD,
∵∠ADB=∠C+∠CAD=∠C+∠C,
∴∠B+∠C+BAC=∠C+∠C+2∠C+∠C=180°,
∴∠C=36°,
故选:B.
5.(2024秋 南岗区校级月考)如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=AK,BN=BK,若∠MKN=44°,则∠P=( )
A.90° B.92° C.96° D.98°
【解答】解:∵PA=PB,∴∠A=∠B,
∵AM=AK,BN=BK,
∴∠AKM=∠AMK=∠BKN=∠BNK,
∵∠MKN=44°,
∴∠AKM=∠BKN=(180°﹣44°)=68°,
∴∠A=∠B=180°﹣68°﹣68°=44°,
∴∠P=180°﹣∠A﹣∠B=92°,
故选:B.
6.(2023秋 凤山县期末)如图,OC=CD=DE,若∠BDE=75°,则∠CDE的度数是( )
A.70° B.75° C.80° D.85°
【解答】解:∵OC=CD=DE,
∴∠O=∠ODC,∠DCE=∠DEC,
∴∠DCE=∠O+∠ODC=2∠ODC,
∵∠O+∠OED=3∠ODC=∠BDE=75°,
∴∠ODC=25°,
∵∠CDE+∠ODC=180°﹣∠BDE=105°,
∴∠CDE=105°﹣∠ODC=80°.
故选:C.
7.(2024春 顺河区期末)如图,在四边形ABCD中,∠C=40°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
A.100° B.90° C.70° D.80°
【解答】解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.
∵∠C=40°,
∴∠DAB=140°,
∴∠AA′E+∠A″=40°,
∵∠EA′A=∠EAA′,∠FAD=∠A″,
∴∠EAA′+∠A″AF=40°,
∴∠EAF=140°﹣40°=100°,
故选:A.
8.(2024秋 玄武区校级月考)如图,∠ABC=∠ACB,BD、CD分别平分△ABC的内角∠ABC,外角∠ACF,连接AD.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADB+∠ACD=90°;④△ABD和△ACD都是等腰三角形.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①过D作DM⊥AB于M,DP⊥AC于P,DN⊥BC于N,
∵BD、CD分别平分△ABC的内角∠ABC,外角∠ACF,
∴DM=DN,DP=DN,
∴DM=DP,
∴AD平分∠EAC,
∴∠EAD=∠CAD,
∵∠EAC=∠ABC+∠ACB,∠ACB=∠ABC,
∴∠EAD=∠ABC,
∴AD∥BC,
∵AD∥BC,故①正确;
②∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC=2∠ADB,
即∠ACB=2∠ADB,故②正确;
③∵CD平分∠ACF,
∴∠ACF=2∠ACD,
又∠ACF+∠ACB=180°,∠ACB=2∠ADB,
∴2∠ADB+2∠ACD=180°,
∴∠ADB+∠ACD=90°,故③正确;
④∵BD平分∠ABC,AD∥BC,
∴∠ABD=∠ADB,
∴△ABD是等腰三角形,
∵CD平分∠ACF,AD∥BC,
∴∠ACD=∠ADC,
∴△ACD是等腰三角形.
故④正确,
故选:D.
二.填空题(共8小题)
9.(2024春 城关区校级期末)如图,已知AB=CB,要使四边形ABCD成为一个轴对称图形,还需添加一个条件,你添加的条件是 AD=CD .(只需写一个,不添加辅助线)
【解答】解:AD=CD,
理由:在△ABD与△CBD中,,
∴△ABD≌△CBD,
∴四边形ABCD是一个轴对称图形,
故答案为:AD=CD.
10.(2024秋 六合区校级月考)如图,∠A=30°,∠C'=60°,△ABC与△A'B'C'关于直线l对称,则∠B= 90° .
【解答】解:∵△ABC与△A′B′C′关于直线l对称,
∴△ABC≌△A′B′C′,
∴∠C=∠C′=60°,
∵∠A=30°,
∴∠B=180°﹣∠A﹣∠C=90°,
故答案为:90°.
11.(2024秋 玄武区校级月考)在△ABC中,AB=AC,AB的垂直平分线与边AC所在的直线相交所得的锐角为40°,则∠C的度数为 65°或25° .
【解答】解:如图,当AB的垂直平分线与边AC相交于点D时,∠ADE=40°,则∠A=90°﹣40°=50°,
∵AB=AC,
∴∠B=∠C=(180°﹣50°)÷2=65°.
如图,当AB边的垂直平分线与CA的延长线交于点D,∠ADE=40°,则∠DAE=90°﹣40°=50°,
∴∠BAC=180°﹣50°=130°.
∵AB=AC,
∴∠B=∠C=(180°﹣130°)÷2=25°.
综上所述:∠C为65°或25°.
故答案为:65°或25°.
12.(2024秋 海淀区校级月考)如图,在△ABC中,∠ABC=90°,∠ACB=60°,BD⊥AC,垂足为D.若CD=2,则AC的长为 8 .
【解答】解:∵∠ABC=90°,∠ACB=60°,BD⊥AC,
∴∠CBD=180°﹣∠C﹣∠BDC=30°,
∴BC=2CD=4,
∵∠A=180°﹣∠ABC﹣∠ACB=30°,
∴AC=2BC=8,
故答案为:8.
13.(2024秋 西湖区校级月考)如图.在△ABC中,按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,作直线MN交AB于点D,连结CD,若AB=5,AC=4,则△ACD的周长为 9 .
【解答】解:由作图过程可知,直线MN为线段BC的垂直平分线,
∴CD=BD,
∴△ACD的周长为AC+AD+CD=AC+AD+BD=AC+AB=4+5=9.
故答案为:9.
14.(2024秋 虎丘区校级月考)若△ABC和△ADE均为等腰三角形,且AB=AC=AD=AE,当∠ABC和∠ADE互余时,称△ABC与△ADE互为“底余等腰三角形”,△ABC的边BC上的高AH叫做△ADE的“余高”.如图,△ABC与△ADE互为“底余等腰三角形”.
(1)若连接BD,CE,判断△ABD与△ACE是否互为“底余等腰三角形”: 是 (填“是”或“否”);
(2)当∠BAC=90°时,若△ADE的“余高”AH=3,则DE= 6 .
【解答】解:(1)如图1,连接BD、CE,
∵AB=AC=AD=AE,
∴∠ABC=∠ACB,∠ADE=∠AED,∠ADB=∠ABD,∠AEC=∠ACE,
∴∠ABC+∠ACB+∠ADE+∠AED=2(∠ABC+∠ADE),∠ADB+∠ABD+∠AEC+∠ACE=2(∠ADB+∠AEC),
∵∠ABC+∠ADE=90°,
∴2(∠ABC+∠ADE)=180°,
∵由四边形BDEC内角和可得∠ABC+∠ACB+∠ADE+∠AED+∠ADB+∠ABD+∠AEC+∠ACE=360°,
∴2(∠ABC+∠ADE)+2(∠ADB+∠AEC)=360°,
∴2(∠ADB+∠AEC)=180°,
∴∠ADB+∠AEC=90°,
∴△ABD与△ACE互为“底余等腰三角形”,
故答案为:是.
(2)如图:
∵∠BAC=90°,AB=AC=AD=AE,
∴∠B=∠C=45°,
∵∠B+∠D=90°,
∴∠D=45°,
∴∠D=∠E=∠B=∠C=45°,
∴△ADE≌△ABC(AAS),
∴DE=BC,
∵AB=AC,AH⊥BC,
∴BH=CH,∠HAB=∠HAC=45°,
∴,
∴DE=BC=6,
故答案为:6.
15.(2024秋 姑苏区校级月考)如图,点B,F,D在射线AM上,点G,C,E在射线AN上,且AB=BC=CD=DE=EF=FG=GA,则∠A= °.
【解答】解:∵AB=BC=CD=DE=EF=FG=GA,设∠A=x,
则∠AFG=∠ACB=x,∠CGF=∠CEF=∠CBF=∠CDF=2x,
∠ECD=∠CED=∠EFD=∠EDF=3x,而∠A+∠CED+∠EDF=180°,
故x=,
即∠A=,
故答案为:.
16.(2024 武威三模)如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为 10 .
【解答】解:∵BO为∠ABC的平分线,CO为∠ACB的平分线,
∴∠ABO=∠CBO,∠ACO=∠BCO,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠BCO,
∴∠ABO=∠MOB,∠NOC=∠ACO,
∴MB=MO,NC=NO,
∴MN=MO+NO=MB+NC,
∵AB=4,AC=6,
∴△AMN周长为AM+MN+AN=AM+MB+AN+NC=AB+AC=10,
故答案为:10
三.解答题(共7小题)
17.(2023秋 宝丰县期末)平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(3,4),C(3,﹣1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标.
【解答】解:(1)如图所示,点A、B、C即为所求;
(2)△ABC的面积为:=5;
(3)若△A1B1C1与△ABC关于x轴对称,则A1(1,﹣4)、B1(3,﹣4)、C1(3,1).
18.(2023秋 乌鲁木齐期末)如图,直线AB∥CD,若∠1=60°,∠2=30°,求证:△FCE是等腰三角形.
【解答】证明:∵AB∥CD,
∴∠DFE=∠1=60°,
∵∠DFE=∠2+∠E,∠DFE=60°,∠2=30°,
∴∠2=∠E,
∴CF=EF,
∴△FCE是等腰三角形.
19.(2024秋 廊坊期中)如图,在△ABC中,AC=BC,CF为△ABC的角平分线,边AC的垂直平分线分别交AC,CF,CB于点D,O,E,连接OA、OB.
(1)不添加辅助线,请直接写出图中的等腰三角形(△ABC除外),并用“≌”表示全等的等腰三角形.
(2)若∠CAB=65°,求∠BOE的度数.(可直接利用(1)的结论)
【解答】解:(1)等腰三角形有△OAB,△OAC,△OBC;
∵AC=BC,CF 为△ABC的角平分线,
∴CF垂直平分边AB,
∴OA=OB,
∵边AC 的垂直平分线分别交AC,CF,CB于点D,O,E,
∴OA=OC,
∴OA=OC=OB,
∴△OAB,△OAC,△OBC为等腰三角形,
在△OAC和△OBC中,
,
∴△OAC≌△OBC(SSS);
(2)∵AC=BC,∠CAB=65°,
∴∠CBA=∠CAB=65°,∠ACB=180°﹣∠CBA﹣∠CAB=50°
∵CF为△ABC的角平分线,
∵DE⊥AC,
∴∠DEC=180°﹣∠EDC﹣∠ACB=180°﹣90°﹣50°=40°.
∵△OBC 为等腰三角形,
∴∠CBO=∠BCF=25°,
∴∠BOE=∠DEC﹣∠CBO=40°﹣25°=15°.
20.(2024秋 沭阳县校级月考)如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)若∠ACB=110°,则∠MCN的度数为 40° ;
(2)若∠ACB=α,则∠MCN的度数为 2α﹣180° ;(用含α的代数式表示)
(3)连接FC,试证明FC平分∠MCN.
【解答】(1)解:∵DM,EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∵∠A+∠B+∠ACM+∠BCN+∠MCN=180°,∠ACB=∠ACM+∠BCN+∠MCN=110°,
∴∠A+∠B=70°,
∴∠A+∠B+∠ACM+∠BCN=140°,
∴∠MCN=40°,
故答案为:40°;
(2)解:∵DM,EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∵∠A+∠B+∠ACM+∠BCN+∠MCN=180°,∠ACB=∠ACM+∠BCN+∠MCN=α,
∴∠A+∠B=180°﹣α,
∴∠A+∠B+∠ACM+∠BCN=2(180°﹣α)=360°﹣2α,
∴∠MCN=180°﹣(360°﹣2α)=2α﹣180°,
故答案为:2α﹣180°;
(3)证明:如图,连接AF、BF,
由题意可得AF=CF,BF=CF,AM=CM,BN=CN,
∴AF=BF,∠ACF=∠CAF,∠BCF=∠CBF,∠CAB=∠ACM,∠CBA=∠BCN,
∴∠BAF=∠ABF,
∵∠MCF=∠ACF﹣∠ACM=∠CAF﹣∠CAM=∠BAF,∠NCF=∠BCF﹣∠BCN=∠CBF﹣∠CBN=∠ABF,
∴∠MCF=∠NCF,
∴FC平分∠MCN.
21.(2024秋 靖江市校级月考)如图,已知AB∥CD,∠BAC的角平分线与CD交于点E,F为射线AB上的一个动点,连接EF,过点C作CG⊥EF,且FG=EG.
(1)已知∠BAC=70°,求∠AEF的度数.
(2)若∠AEF=α,求∠ECG的度数.
【解答】解:(1)如图所示,连接CF,
∵CG⊥EF,FG=EG.
∴CF=CE,
∴∠CFE=∠CEF,
∵AB∥CD,
∴∠BFE=∠CEF,
∴∠CFE=∠BFE,
∵AB∥CD,
∴∠BAE=∠AEC,
∵AE平分∠BAC,
∴∠BAE=∠CAE=∠BAC=35°
∴∠AEC=∠CAE,
∴CA=CE,
∴CF=CA,
∴∠CFA=∠CAF=70°,
∴∠CEF=∠CFE=∠BFE=(180°﹣70°)==55°,
∵∠AEC=35°,
∴∠AEF=∠CEF﹣∠AEC=20°;
(2)设∠AEC=β,
∵∠AEF=α,
∴∠CEF=∠AEF+∠AEC=α+β,
∵AB∥CD,
∴∠BAE=∠AEC=β,
∵AE平分∠BAC,
∴∠BAC=2∠BAE=2β,
∴∠AEC=∠EAC,
∴CA=CE,
∵CG⊥EF,FG=EG,
∴CG垂直平分EF,
∴CF=CE,
∴CA=CF,∠CFE=∠CEF=α+β,
∴∠CFA=∠CAF=2β,
∵AB∥CD,
∴∠AFE+∠CEF=180°,
∴∠AFC+∠CFE+∠CEF=180°,
即2β+α+β+α+β=180°,
∴β=,
∴α+β=,
∵∠CGE=90°,
∴∠ECG=90°﹣∠CEF=90°﹣(α+β)=45°﹣,
∴∠ECG的度数为45°﹣.
22.(2024秋 高州市校级月考)如图1,A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.
现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选方案1:水厂建在C点,修自来水管道到A村,再到B村(即AC+AB).(如图2)方案2:作A点关于直线CD的对称点A',连接A'B交CD于M点,水厂建在M点处,分别向两村修管道AM和BM.(即AM+BM)(如图3)从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工,请利用已有条件分别进行计算,判断哪种方案更合适.
【解答】解:方案1:如图2中,过点A作AE⊥BD于点E,
∵∠ACD]=∠CDE=∠AED=90°,
∴四边形ACDE是矩形,
∴DE=AC=1,
∵AC=1,BD=4,
∴BE=BD﹣DE=4﹣1=3,
在Rt△ABE中,AB2=AE2+BE2,
∴,
∴AC+AB=1+5=6;
方案2:如图3中,过A′作A′H⊥BD交BD延长线于点H,
∵AA′⊥CD,BH⊥CD,
∴AA′∥BH,
∵A′H⊥BH,
∴CD=A′H=4,
同理A′C=DH,
∵AC=A′C=1,
∴BH=BD+DH=BD+A′C=BD+AC=5,
∴,
∵AM′=AM,
∴,
∵,
∴方案1路线短,更合适.
23.(2024秋 高新区月考)如图1,已知A,B为直线MN同侧的两点,连接AP,BP,若∠APM=∠BPN,则称点P为点A,B关于直线MN的“等角点”.
【理解运用】
(1)如图2,在△ABC中,D为BC上一点,点D、E关于直线AB对称,连接EB并延长至点F,判断点B是否为点D、F关于直线AB的“等角点”,并说明理由;
【拓展提升】
(2)如图3,在△ABC中,∠ABC,∠BAC的平分线交于点O,点O到AC的距离为2,直线l垂直平分边BC,点P为O,B关于直线l“等角点”,连接OP,BP,当∠ACB=60°时,OP+BP的值为 4 .
【解答】解:(1)点B是点D、F关于直线AB的“等角点”,理由如下:
如图,
∵点D、E关于直线AB对称,
∴∠ABD=∠ABE,
∵∠ABE=∠FBM,
∴∠ABD=∠FBM,
∴点B是点D、F关于直线AB的“等角点”;
(2)如图,连接OC,PC,过点O作OD⊥AC于D,
∵∠ABC,∠BAC的平分线交于点O,
∴OC平分∠ACB,
∴∠OCD=∠ACB=30°,
∵OD⊥AC,
∴OC=2OD=4,
∵直线l垂直平分边BC,
∴∠BPE=∠CPE,BP=CP,
∵点P为O,B关于直线l“等角点”,
∴∠BPE=∠OPF,
∴∠CPE=∠OPF,
∵∠OPF+∠BPO+∠BPE=180°,
∴∠CPE+∠BPO+∠BPE=180°,
∴O,P,C在同一条直线上,
∴OP+BP=OP+CP=OC=4,
故答案为:4.
一.选择题(共8小题)
1.(2024 滨州)数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是( )
A. B.
C. D.
2.(2024 成都模拟)在平面直角坐标系中,点A(3,﹣2),B(m,n)关于x轴对称,将点B向左平移3个单位长度得到点C,则点C的坐标为( )
A.(3,﹣2) B.(3,2) C.(0,﹣2) D.(0,2)
3.(2024秋 宜兴市校级月考)下列说法:①形状相同的两个三角形是全等三角形;②全等三角形的中线相等;③成轴对称的两个图形中,对应点的连线段被对称轴垂直平分;④两条直角边对应相等的两个直角三角形全等.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
4.(2024秋 凉州区校级期中)如图,在△ABC中,AB=AC,且点D为BC上一点,CD=AD,AB=BD,则∠C为( )
A.30° B.36° C.40° D.45°
5.(2024秋 南岗区校级月考)如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=AK,BN=BK,若∠MKN=44°,则∠P=( )
A.90° B.92° C.96° D.98°
6.(2023秋 凤山县期末)如图,OC=CD=DE,若∠BDE=75°,则∠CDE的度数是( )
A.70° B.75° C.80° D.85°
7.(2024春 顺河区期末)如图,在四边形ABCD中,∠C=40°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
A.100° B.90° C.70° D.80°
8.(2024秋 玄武区校级月考)如图,∠ABC=∠ACB,BD、CD分别平分△ABC的内角∠ABC,外角∠ACF,连接AD.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADB+∠ACD=90°;④△ABD和△ACD都是等腰三角形.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共8小题)
9.(2024春 城关区校级期末)如图,已知AB=CB,要使四边形ABCD成为一个轴对称图形,还需添加一个条件,你添加的条件是 .(只需写一个,不添加辅助线)
10.(2024秋 六合区校级月考)如图,∠A=30°,∠C'=60°,△ABC与△A'B'C'关于直线l对称,则∠B= .
11.(2024秋 玄武区校级月考)在△ABC中,AB=AC,AB的垂直平分线与边AC所在的直线相交所得的锐角为40°,则∠C的度数为 .
12.(2024秋 海淀区校级月考)如图,在△ABC中,∠ABC=90°,∠ACB=60°,BD⊥AC,垂足为D.若CD=2,则AC的长为 .
13.(2024秋 西湖区校级月考)如图.在△ABC中,按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,作直线MN交AB于点D,连结CD,若AB=5,AC=4,则△ACD的周长为 .
14.(2024秋 虎丘区校级月考)若△ABC和△ADE均为等腰三角形,且AB=AC=AD=AE,当∠ABC和∠ADE互余时,称△ABC与△ADE互为“底余等腰三角形”,△ABC的边BC上的高AH叫做△ADE的“余高”.如图,△ABC与△ADE互为“底余等腰三角形”.
(1)若连接BD,CE,判断△ABD与△ACE是否互为“底余等腰三角形”: (填“是”或“否”);
(2)当∠BAC=90°时,若△ADE的“余高”AH=3,则DE= .
15.(2024秋 姑苏区校级月考)如图,点B,F,D在射线AM上,点G,C,E在射线AN上,且AB=BC=CD=DE=EF=FG=GA,则∠A= °.
16.(2024 武威三模)如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为 .
三.解答题(共7小题)
17.(2023秋 宝丰县期末)平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(3,4),C(3,﹣1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标.
18.(2023秋 乌鲁木齐期末)如图,直线AB∥CD,若∠1=60°,∠2=30°,求证:△FCE是等腰三角形.
19.(2024秋 廊坊期中)如图,在△ABC中,AC=BC,CF为△ABC的角平分线,边AC的垂直平分线分别交AC,CF,CB于点D,O,E,连接OA、OB.
(1)不添加辅助线,请直接写出图中的等腰三角形(△ABC除外),并用“≌”表示全等的等腰三角形.
(2)若∠CAB=65°,求∠BOE的度数.(可直接利用(1)的结论)
20.(2024秋 沭阳县校级月考)如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)若∠ACB=110°,则∠MCN的度数为 ;
(2)若∠ACB=α,则∠MCN的度数为 ;(用含α的代数式表示)
(3)连接FC,试证明FC平分∠MCN.
21.(2024秋 靖江市校级月考)如图,已知AB∥CD,∠BAC的角平分线与CD交于点E,F为射线AB上的一个动点,连接EF,过点C作CG⊥EF,且FG=EG.
(1)已知∠BAC=70°,求∠AEF的度数.
(2)若∠AEF=α,求∠ECG的度数.
22.(2024秋 高州市校级月考)如图1,A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.
现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选方案1:水厂建在C点,修自来水管道到A村,再到B村(即AC+AB).(如图2)方案2:作A点关于直线CD的对称点A',连接A'B交CD于M点,水厂建在M点处,分别向两村修管道AM和BM.(即AM+BM)(如图3)从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工,请利用已有条件分别进行计算,判断哪种方案更合适.
23.(2024秋 高新区月考)如图1,已知A,B为直线MN同侧的两点,连接AP,BP,若∠APM=∠BPN,则称点P为点A,B关于直线MN的“等角点”.
【理解运用】
(1)如图2,在△ABC中,D为BC上一点,点D、E关于直线AB对称,连接EB并延长至点F,判断点B是否为点D、F关于直线AB的“等角点”,并说明理由;
【拓展提升】
(2)如图3,在△ABC中,∠ABC,∠BAC的平分线交于点O,点O到AC的距离为2,直线l垂直平分边BC,点P为O,B关于直线l“等角点”,连接OP,BP,当∠ACB=60°时,OP+BP的值为 .
第13章轴对称复习检测卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共8小题)
1.(2024 滨州)数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是( )
A. B.
C. D.
【解答】解:A、是轴对称图形;
B、不是轴对称图形;
C、是轴对称图形;
D、是轴对称图形;
故选:B.
2.(2024 成都模拟)在平面直角坐标系中,点A(3,﹣2),B(m,n)关于x轴对称,将点B向左平移3个单位长度得到点C,则点C的坐标为( )
A.(3,﹣2) B.(3,2) C.(0,﹣2) D.(0,2)
【解答】解:∵点A(3,﹣2),B(m,n)关于x轴对称,
∴点B的坐标为(3,2),
∴将点B向左平移3个单位长度得到点C,则点C的坐标为(0,2).
故选:D.
3.(2024秋 宜兴市校级月考)下列说法:①形状相同的两个三角形是全等三角形;②全等三角形的中线相等;③成轴对称的两个图形中,对应点的连线段被对称轴垂直平分;④两条直角边对应相等的两个直角三角形全等.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①形状相同的两个三角形是相似三角形,不一定是全等三角形,只有形状相同,大小也相等的两个三角形才是全等三角形,不符合题意;
②全等三角形对应边上的中线相等,不符合题意;
③成轴对称的两个图形中,对应点的连线段被对称轴垂直平分,符合题意;
④两个直角三角形的两条直角边对应相等,这两个直角三角形全等,符合全等三角形的判定定理“SAS”,符合题意.
综上所述,正确的说法有③④共2个.
故选:B.
4.(2024秋 凉州区校级期中)如图,在△ABC中,AB=AC,且点D为BC上一点,CD=AD,AB=BD,则∠C为( )
A.30° B.36° C.40° D.45°
【解答】解:∵AB=AC,CD=AD,AB=BD,
∴∠B=∠C=∠CAD,∠ADB=∠BAD,
∵∠ADB=∠C+∠CAD=∠C+∠C,
∴∠B+∠C+BAC=∠C+∠C+2∠C+∠C=180°,
∴∠C=36°,
故选:B.
5.(2024秋 南岗区校级月考)如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=AK,BN=BK,若∠MKN=44°,则∠P=( )
A.90° B.92° C.96° D.98°
【解答】解:∵PA=PB,∴∠A=∠B,
∵AM=AK,BN=BK,
∴∠AKM=∠AMK=∠BKN=∠BNK,
∵∠MKN=44°,
∴∠AKM=∠BKN=(180°﹣44°)=68°,
∴∠A=∠B=180°﹣68°﹣68°=44°,
∴∠P=180°﹣∠A﹣∠B=92°,
故选:B.
6.(2023秋 凤山县期末)如图,OC=CD=DE,若∠BDE=75°,则∠CDE的度数是( )
A.70° B.75° C.80° D.85°
【解答】解:∵OC=CD=DE,
∴∠O=∠ODC,∠DCE=∠DEC,
∴∠DCE=∠O+∠ODC=2∠ODC,
∵∠O+∠OED=3∠ODC=∠BDE=75°,
∴∠ODC=25°,
∵∠CDE+∠ODC=180°﹣∠BDE=105°,
∴∠CDE=105°﹣∠ODC=80°.
故选:C.
7.(2024春 顺河区期末)如图,在四边形ABCD中,∠C=40°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为( )
A.100° B.90° C.70° D.80°
【解答】解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.
∵∠C=40°,
∴∠DAB=140°,
∴∠AA′E+∠A″=40°,
∵∠EA′A=∠EAA′,∠FAD=∠A″,
∴∠EAA′+∠A″AF=40°,
∴∠EAF=140°﹣40°=100°,
故选:A.
8.(2024秋 玄武区校级月考)如图,∠ABC=∠ACB,BD、CD分别平分△ABC的内角∠ABC,外角∠ACF,连接AD.以下结论:①AD∥BC;②∠ACB=2∠ADB;③∠ADB+∠ACD=90°;④△ABD和△ACD都是等腰三角形.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:①过D作DM⊥AB于M,DP⊥AC于P,DN⊥BC于N,
∵BD、CD分别平分△ABC的内角∠ABC,外角∠ACF,
∴DM=DN,DP=DN,
∴DM=DP,
∴AD平分∠EAC,
∴∠EAD=∠CAD,
∵∠EAC=∠ABC+∠ACB,∠ACB=∠ABC,
∴∠EAD=∠ABC,
∴AD∥BC,
∵AD∥BC,故①正确;
②∵AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,∠ABC=∠ACB,
∴∠ABC=∠ACB=2∠DBC=2∠ADB,
即∠ACB=2∠ADB,故②正确;
③∵CD平分∠ACF,
∴∠ACF=2∠ACD,
又∠ACF+∠ACB=180°,∠ACB=2∠ADB,
∴2∠ADB+2∠ACD=180°,
∴∠ADB+∠ACD=90°,故③正确;
④∵BD平分∠ABC,AD∥BC,
∴∠ABD=∠ADB,
∴△ABD是等腰三角形,
∵CD平分∠ACF,AD∥BC,
∴∠ACD=∠ADC,
∴△ACD是等腰三角形.
故④正确,
故选:D.
二.填空题(共8小题)
9.(2024春 城关区校级期末)如图,已知AB=CB,要使四边形ABCD成为一个轴对称图形,还需添加一个条件,你添加的条件是 AD=CD .(只需写一个,不添加辅助线)
【解答】解:AD=CD,
理由:在△ABD与△CBD中,,
∴△ABD≌△CBD,
∴四边形ABCD是一个轴对称图形,
故答案为:AD=CD.
10.(2024秋 六合区校级月考)如图,∠A=30°,∠C'=60°,△ABC与△A'B'C'关于直线l对称,则∠B= 90° .
【解答】解:∵△ABC与△A′B′C′关于直线l对称,
∴△ABC≌△A′B′C′,
∴∠C=∠C′=60°,
∵∠A=30°,
∴∠B=180°﹣∠A﹣∠C=90°,
故答案为:90°.
11.(2024秋 玄武区校级月考)在△ABC中,AB=AC,AB的垂直平分线与边AC所在的直线相交所得的锐角为40°,则∠C的度数为 65°或25° .
【解答】解:如图,当AB的垂直平分线与边AC相交于点D时,∠ADE=40°,则∠A=90°﹣40°=50°,
∵AB=AC,
∴∠B=∠C=(180°﹣50°)÷2=65°.
如图,当AB边的垂直平分线与CA的延长线交于点D,∠ADE=40°,则∠DAE=90°﹣40°=50°,
∴∠BAC=180°﹣50°=130°.
∵AB=AC,
∴∠B=∠C=(180°﹣130°)÷2=25°.
综上所述:∠C为65°或25°.
故答案为:65°或25°.
12.(2024秋 海淀区校级月考)如图,在△ABC中,∠ABC=90°,∠ACB=60°,BD⊥AC,垂足为D.若CD=2,则AC的长为 8 .
【解答】解:∵∠ABC=90°,∠ACB=60°,BD⊥AC,
∴∠CBD=180°﹣∠C﹣∠BDC=30°,
∴BC=2CD=4,
∵∠A=180°﹣∠ABC﹣∠ACB=30°,
∴AC=2BC=8,
故答案为:8.
13.(2024秋 西湖区校级月考)如图.在△ABC中,按以下步骤作图:分别以点B和点C为圆心,大于BC一半的长为半径作圆弧,两弧相交于点M和点N,作直线MN交AB于点D,连结CD,若AB=5,AC=4,则△ACD的周长为 9 .
【解答】解:由作图过程可知,直线MN为线段BC的垂直平分线,
∴CD=BD,
∴△ACD的周长为AC+AD+CD=AC+AD+BD=AC+AB=4+5=9.
故答案为:9.
14.(2024秋 虎丘区校级月考)若△ABC和△ADE均为等腰三角形,且AB=AC=AD=AE,当∠ABC和∠ADE互余时,称△ABC与△ADE互为“底余等腰三角形”,△ABC的边BC上的高AH叫做△ADE的“余高”.如图,△ABC与△ADE互为“底余等腰三角形”.
(1)若连接BD,CE,判断△ABD与△ACE是否互为“底余等腰三角形”: 是 (填“是”或“否”);
(2)当∠BAC=90°时,若△ADE的“余高”AH=3,则DE= 6 .
【解答】解:(1)如图1,连接BD、CE,
∵AB=AC=AD=AE,
∴∠ABC=∠ACB,∠ADE=∠AED,∠ADB=∠ABD,∠AEC=∠ACE,
∴∠ABC+∠ACB+∠ADE+∠AED=2(∠ABC+∠ADE),∠ADB+∠ABD+∠AEC+∠ACE=2(∠ADB+∠AEC),
∵∠ABC+∠ADE=90°,
∴2(∠ABC+∠ADE)=180°,
∵由四边形BDEC内角和可得∠ABC+∠ACB+∠ADE+∠AED+∠ADB+∠ABD+∠AEC+∠ACE=360°,
∴2(∠ABC+∠ADE)+2(∠ADB+∠AEC)=360°,
∴2(∠ADB+∠AEC)=180°,
∴∠ADB+∠AEC=90°,
∴△ABD与△ACE互为“底余等腰三角形”,
故答案为:是.
(2)如图:
∵∠BAC=90°,AB=AC=AD=AE,
∴∠B=∠C=45°,
∵∠B+∠D=90°,
∴∠D=45°,
∴∠D=∠E=∠B=∠C=45°,
∴△ADE≌△ABC(AAS),
∴DE=BC,
∵AB=AC,AH⊥BC,
∴BH=CH,∠HAB=∠HAC=45°,
∴,
∴DE=BC=6,
故答案为:6.
15.(2024秋 姑苏区校级月考)如图,点B,F,D在射线AM上,点G,C,E在射线AN上,且AB=BC=CD=DE=EF=FG=GA,则∠A= °.
【解答】解:∵AB=BC=CD=DE=EF=FG=GA,设∠A=x,
则∠AFG=∠ACB=x,∠CGF=∠CEF=∠CBF=∠CDF=2x,
∠ECD=∠CED=∠EFD=∠EDF=3x,而∠A+∠CED+∠EDF=180°,
故x=,
即∠A=,
故答案为:.
16.(2024 武威三模)如图,在△ABC中,AB=4,AC=6,∠ABC和∠ACB的平分线交于O点,过点O作BC的平行线交AB于M点,交AC于N点,则△AMN的周长为 10 .
【解答】解:∵BO为∠ABC的平分线,CO为∠ACB的平分线,
∴∠ABO=∠CBO,∠ACO=∠BCO,
∵MN∥BC,
∴∠MOB=∠OBC,∠NOC=∠BCO,
∴∠ABO=∠MOB,∠NOC=∠ACO,
∴MB=MO,NC=NO,
∴MN=MO+NO=MB+NC,
∵AB=4,AC=6,
∴△AMN周长为AM+MN+AN=AM+MB+AN+NC=AB+AC=10,
故答案为:10
三.解答题(共7小题)
17.(2023秋 宝丰县期末)平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(3,4),C(3,﹣1).
(1)试在平面直角坐标系中,标出A、B、C三点;
(2)求△ABC的面积.
(3)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标.
【解答】解:(1)如图所示,点A、B、C即为所求;
(2)△ABC的面积为:=5;
(3)若△A1B1C1与△ABC关于x轴对称,则A1(1,﹣4)、B1(3,﹣4)、C1(3,1).
18.(2023秋 乌鲁木齐期末)如图,直线AB∥CD,若∠1=60°,∠2=30°,求证:△FCE是等腰三角形.
【解答】证明:∵AB∥CD,
∴∠DFE=∠1=60°,
∵∠DFE=∠2+∠E,∠DFE=60°,∠2=30°,
∴∠2=∠E,
∴CF=EF,
∴△FCE是等腰三角形.
19.(2024秋 廊坊期中)如图,在△ABC中,AC=BC,CF为△ABC的角平分线,边AC的垂直平分线分别交AC,CF,CB于点D,O,E,连接OA、OB.
(1)不添加辅助线,请直接写出图中的等腰三角形(△ABC除外),并用“≌”表示全等的等腰三角形.
(2)若∠CAB=65°,求∠BOE的度数.(可直接利用(1)的结论)
【解答】解:(1)等腰三角形有△OAB,△OAC,△OBC;
∵AC=BC,CF 为△ABC的角平分线,
∴CF垂直平分边AB,
∴OA=OB,
∵边AC 的垂直平分线分别交AC,CF,CB于点D,O,E,
∴OA=OC,
∴OA=OC=OB,
∴△OAB,△OAC,△OBC为等腰三角形,
在△OAC和△OBC中,
,
∴△OAC≌△OBC(SSS);
(2)∵AC=BC,∠CAB=65°,
∴∠CBA=∠CAB=65°,∠ACB=180°﹣∠CBA﹣∠CAB=50°
∵CF为△ABC的角平分线,
∵DE⊥AC,
∴∠DEC=180°﹣∠EDC﹣∠ACB=180°﹣90°﹣50°=40°.
∵△OBC 为等腰三角形,
∴∠CBO=∠BCF=25°,
∴∠BOE=∠DEC﹣∠CBO=40°﹣25°=15°.
20.(2024秋 沭阳县校级月考)如图,在△ABC中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,DM与EN相交于点F.
(1)若∠ACB=110°,则∠MCN的度数为 40° ;
(2)若∠ACB=α,则∠MCN的度数为 2α﹣180° ;(用含α的代数式表示)
(3)连接FC,试证明FC平分∠MCN.
【解答】(1)解:∵DM,EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∵∠A+∠B+∠ACM+∠BCN+∠MCN=180°,∠ACB=∠ACM+∠BCN+∠MCN=110°,
∴∠A+∠B=70°,
∴∠A+∠B+∠ACM+∠BCN=140°,
∴∠MCN=40°,
故答案为:40°;
(2)解:∵DM,EN分别垂直平分AC和BC,
∴AM=CM,BN=CN,
∴∠A=∠ACM,∠B=∠BCN,
∵∠A+∠B+∠ACM+∠BCN+∠MCN=180°,∠ACB=∠ACM+∠BCN+∠MCN=α,
∴∠A+∠B=180°﹣α,
∴∠A+∠B+∠ACM+∠BCN=2(180°﹣α)=360°﹣2α,
∴∠MCN=180°﹣(360°﹣2α)=2α﹣180°,
故答案为:2α﹣180°;
(3)证明:如图,连接AF、BF,
由题意可得AF=CF,BF=CF,AM=CM,BN=CN,
∴AF=BF,∠ACF=∠CAF,∠BCF=∠CBF,∠CAB=∠ACM,∠CBA=∠BCN,
∴∠BAF=∠ABF,
∵∠MCF=∠ACF﹣∠ACM=∠CAF﹣∠CAM=∠BAF,∠NCF=∠BCF﹣∠BCN=∠CBF﹣∠CBN=∠ABF,
∴∠MCF=∠NCF,
∴FC平分∠MCN.
21.(2024秋 靖江市校级月考)如图,已知AB∥CD,∠BAC的角平分线与CD交于点E,F为射线AB上的一个动点,连接EF,过点C作CG⊥EF,且FG=EG.
(1)已知∠BAC=70°,求∠AEF的度数.
(2)若∠AEF=α,求∠ECG的度数.
【解答】解:(1)如图所示,连接CF,
∵CG⊥EF,FG=EG.
∴CF=CE,
∴∠CFE=∠CEF,
∵AB∥CD,
∴∠BFE=∠CEF,
∴∠CFE=∠BFE,
∵AB∥CD,
∴∠BAE=∠AEC,
∵AE平分∠BAC,
∴∠BAE=∠CAE=∠BAC=35°
∴∠AEC=∠CAE,
∴CA=CE,
∴CF=CA,
∴∠CFA=∠CAF=70°,
∴∠CEF=∠CFE=∠BFE=(180°﹣70°)==55°,
∵∠AEC=35°,
∴∠AEF=∠CEF﹣∠AEC=20°;
(2)设∠AEC=β,
∵∠AEF=α,
∴∠CEF=∠AEF+∠AEC=α+β,
∵AB∥CD,
∴∠BAE=∠AEC=β,
∵AE平分∠BAC,
∴∠BAC=2∠BAE=2β,
∴∠AEC=∠EAC,
∴CA=CE,
∵CG⊥EF,FG=EG,
∴CG垂直平分EF,
∴CF=CE,
∴CA=CF,∠CFE=∠CEF=α+β,
∴∠CFA=∠CAF=2β,
∵AB∥CD,
∴∠AFE+∠CEF=180°,
∴∠AFC+∠CFE+∠CEF=180°,
即2β+α+β+α+β=180°,
∴β=,
∴α+β=,
∵∠CGE=90°,
∴∠ECG=90°﹣∠CEF=90°﹣(α+β)=45°﹣,
∴∠ECG的度数为45°﹣.
22.(2024秋 高州市校级月考)如图1,A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.
现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选方案1:水厂建在C点,修自来水管道到A村,再到B村(即AC+AB).(如图2)方案2:作A点关于直线CD的对称点A',连接A'B交CD于M点,水厂建在M点处,分别向两村修管道AM和BM.(即AM+BM)(如图3)从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工,请利用已有条件分别进行计算,判断哪种方案更合适.
【解答】解:方案1:如图2中,过点A作AE⊥BD于点E,
∵∠ACD]=∠CDE=∠AED=90°,
∴四边形ACDE是矩形,
∴DE=AC=1,
∵AC=1,BD=4,
∴BE=BD﹣DE=4﹣1=3,
在Rt△ABE中,AB2=AE2+BE2,
∴,
∴AC+AB=1+5=6;
方案2:如图3中,过A′作A′H⊥BD交BD延长线于点H,
∵AA′⊥CD,BH⊥CD,
∴AA′∥BH,
∵A′H⊥BH,
∴CD=A′H=4,
同理A′C=DH,
∵AC=A′C=1,
∴BH=BD+DH=BD+A′C=BD+AC=5,
∴,
∵AM′=AM,
∴,
∵,
∴方案1路线短,更合适.
23.(2024秋 高新区月考)如图1,已知A,B为直线MN同侧的两点,连接AP,BP,若∠APM=∠BPN,则称点P为点A,B关于直线MN的“等角点”.
【理解运用】
(1)如图2,在△ABC中,D为BC上一点,点D、E关于直线AB对称,连接EB并延长至点F,判断点B是否为点D、F关于直线AB的“等角点”,并说明理由;
【拓展提升】
(2)如图3,在△ABC中,∠ABC,∠BAC的平分线交于点O,点O到AC的距离为2,直线l垂直平分边BC,点P为O,B关于直线l“等角点”,连接OP,BP,当∠ACB=60°时,OP+BP的值为 4 .
【解答】解:(1)点B是点D、F关于直线AB的“等角点”,理由如下:
如图,
∵点D、E关于直线AB对称,
∴∠ABD=∠ABE,
∵∠ABE=∠FBM,
∴∠ABD=∠FBM,
∴点B是点D、F关于直线AB的“等角点”;
(2)如图,连接OC,PC,过点O作OD⊥AC于D,
∵∠ABC,∠BAC的平分线交于点O,
∴OC平分∠ACB,
∴∠OCD=∠ACB=30°,
∵OD⊥AC,
∴OC=2OD=4,
∵直线l垂直平分边BC,
∴∠BPE=∠CPE,BP=CP,
∵点P为O,B关于直线l“等角点”,
∴∠BPE=∠OPF,
∴∠CPE=∠OPF,
∵∠OPF+∠BPO+∠BPE=180°,
∴∠CPE+∠BPO+∠BPE=180°,
∴O,P,C在同一条直线上,
∴OP+BP=OP+CP=OC=4,
故答案为:4.
