河南省信阳市息县关店2024-2025学年 八年级人教版数学上册期中压轴卷B(含答案)
文档属性
| 名称 | 河南省信阳市息县关店2024-2025学年 八年级人教版数学上册期中压轴卷B(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 206.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-05 22:34:35 | ||
图片预览


文档简介
2024-2025学年关店八年级人教版数学上册期中压轴卷B
(满分:120分 时间100分钟)
一、选择题:本题共10小题,共30分。
1.在一些美术字中,有的汉字是轴对称图形.下面个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
2.用直角三角板,作的高,下列作法正确的是( )
A. B. C. D.
3.下列长度的三条线段能首尾相接构成三角形的是( )
A. ,, B. ,,
C. ,, D. ,,
4.正十边形的外角和的度数为( )
A. B. C. D.
5.点关于轴的对称的点的坐标是( )
A. , B. C. D.
6.如图,已知,补充下列哪一个条件,
仍不能判定和全等的是( )
A. B. C. D.
7.如图,中,,为中点,把纸片沿对折得到,如图,点和点分别为,上的动点,把纸片沿折叠,使得点落在的外部,如图所示.设,则下列等式成立的是( )
A. B. C. D.
8.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质( )
A. B.
C. D.
9.某班开展“用直尺和圆规作角平分线”的探究活动,各组展示作图痕迹如下,
其中射线为的平分线的有( )
A. 个 B. 个 C. 个 D. 个
10.如图,在平面直角坐标系中,对进行循环往复的轴对称变换,若原来点坐标是,则经过第5次变换后点的对应点的坐标为( )
A. B. C. D.
第II卷(非选择题)
二、填空题:本题共5小题,共15分。
11.如图,小林从点向西直走米后,向左转,再走米,如此重复,小林共走了米回到点,则为______.
12.如图,在中,,,的垂直平分线交于,交于,
若,则_____ _____.
13.如图,在平面直角坐标系中,为坐标原点在中,,若点的坐标为,则第二象限的点的坐标是______.
11题图 12题图 14题图
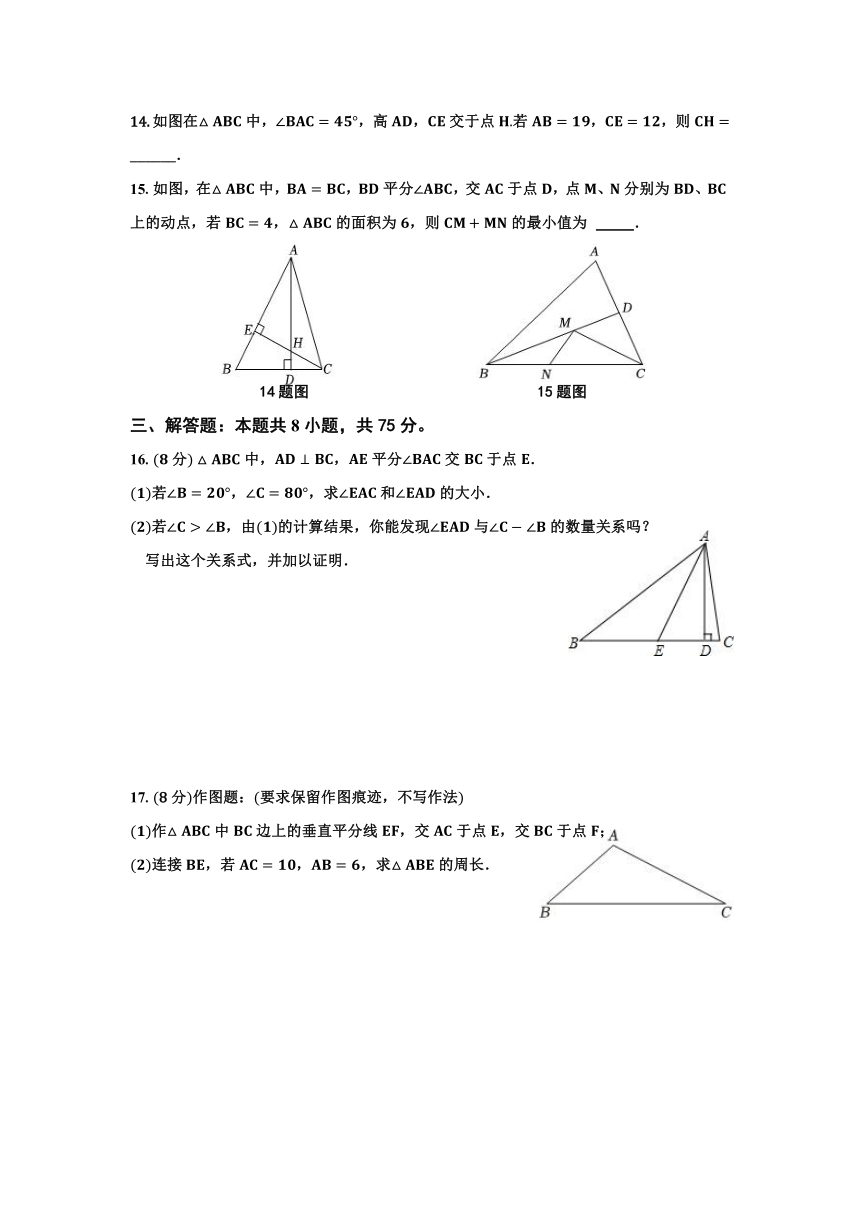
如图在中,,高,交于点若,,则 ______.
15.如图,在中,,平分,交于点,点、分别为、上的动点,若,的面积为,则的最小值为 .
14题图 15题图
三、解答题:本题共8小题,共75分。
16.分中,,平分交于点.
若,,求和的大小.
若,由的计算结果,你能发现与的数量关系吗?
写出这个关系式,并加以证明.
17.8分作图题:要求保留作图痕迹,不写作法
作中边上的垂直平分线,交于点,交于点;
连接,若,,求的周长.
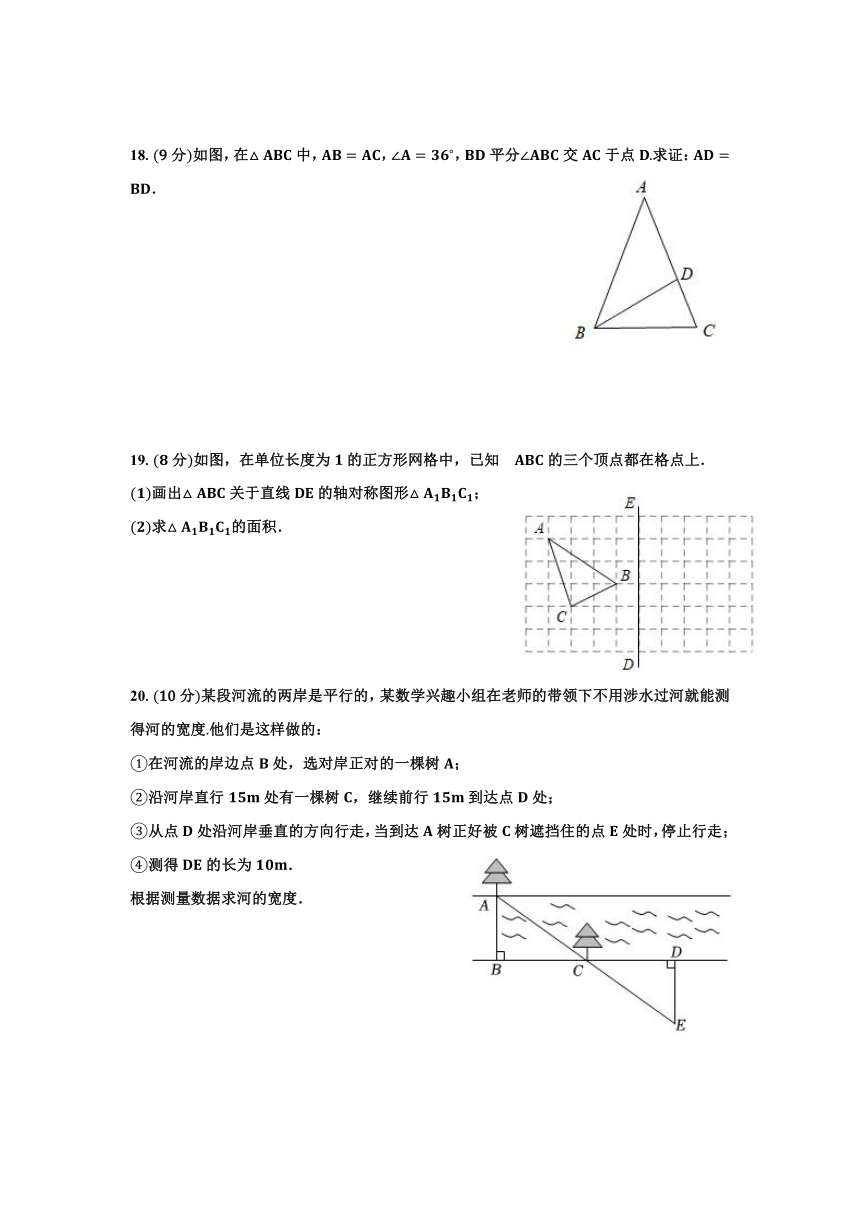
18.9分如图,在中,,,平分交于点求证:.
19.分如图,在单位长度为的正方形网格中,已知的三个顶点都在格点上.
画出关于直线的轴对称图形;
求的面积.
20.10分某段河流的两岸是平行的,某数学兴趣小组在老师的带领下不用涉水过河就能测得河的宽度他们是这样做的:
在河流的岸边点处,选对岸正对的一棵树;
沿河岸直行处有一棵树,继续前行到达点处;
从点处沿河岸垂直的方向行走,当到达树正好被树遮挡住的点处时,停止行走;
测得的长为.
根据测量数据求河的宽度.
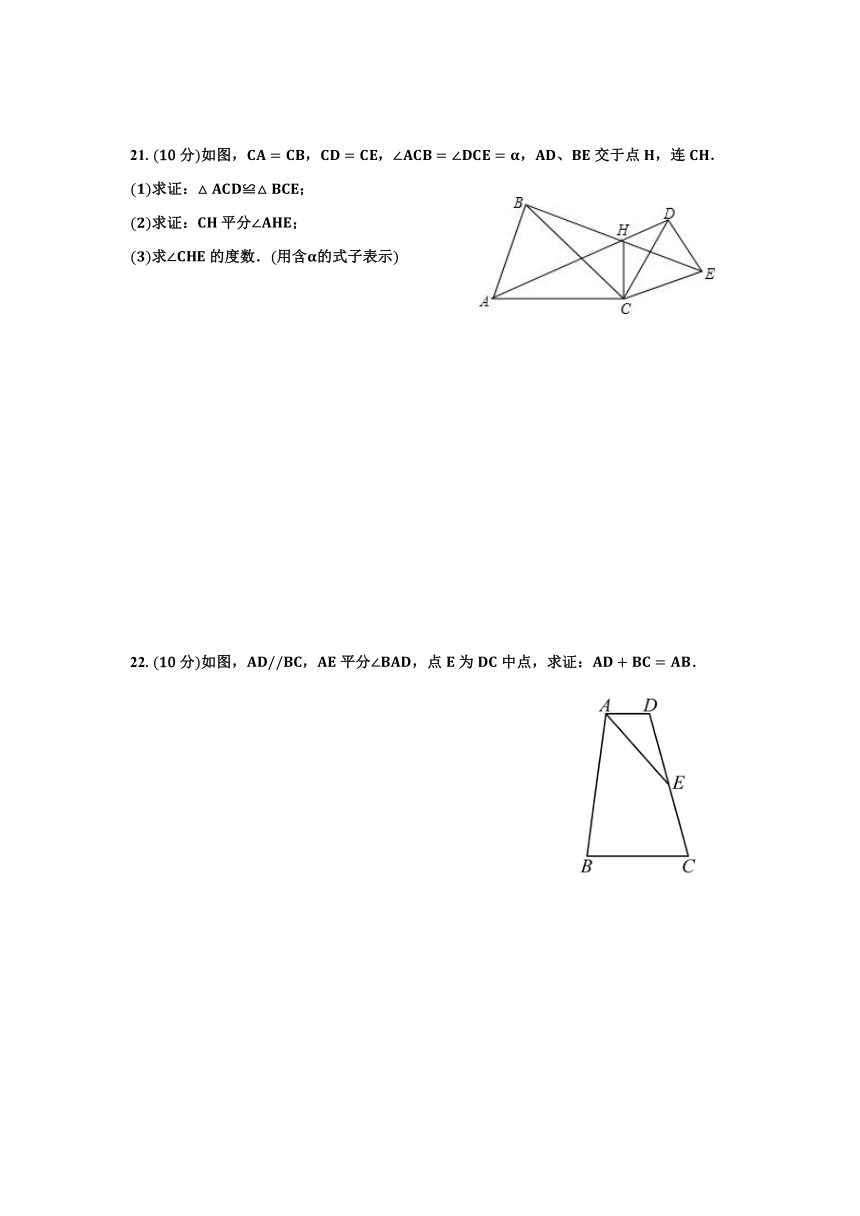
21.10分如图,,,,、交于点,连.
求证:≌;
求证:平分;
求的度数.用含的式子表示
22.10分如图,,平分,点为中点,求证:.
23.11分如图,和均为等边三角形,点,,在同一直线上,连接.
填空:的度数为 ;
线段,之间的数量关系为
如图,和均为等腰直角三角形,,点,,在同一直线上,为中边上的高,连接,请判断的度数及线段,,之间的数量关系,并说明理由.
参考答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
解:如图,
,为中点,
,,
,
如图,设 与交于点,
把纸片沿折叠,
,
在四边形中,,
,
,
,
,
,
由图可知,
.
8.【答案】
解:如图,由作图可知,.
在和中,,
≌,
故选:.
9.【答案】
10.【答案】
11.【答案】
解:设边数为,根据题意,
,
则.
故答案为:.
12.【答案】
解:如图,连接.
的垂直平分线交于,
,
,
.
又在中,,,
.
所以:
故答案是:.
13.【答案】
解:作轴于点,轴于点.
,,
,
,
,
在与中,
,
≌,
,
,,
,
答案为:.
14.【答案】
解:,,
,
,
,,,
,
在和中,
,
≌,
,
,
,
,答案为:.
15.【答案】
【解解:连接,过点作于点,如图:
,平分,
且平分,
是线段的垂直平分线,
,
,
根据“垂线段最短”得:,
即当点在线段上时,为最小,最小值为线段的长,
的面积为,,
,
,
的最小值为.
故答案为:.
16.【答案】解:,,
,
平分,
,
,
,
,
,
;
结论:.
理由:三角形的内角和等于,
,
平分,
,
,
,
,
.
17.【答案】解:如图,直线即为所求.
直线为线段的垂直平分线,
.
的周长为.
18.【答案】证明:,,
,
平分交于点,
,
,
,
19.【答案】
的面积为
20.【答案】解:河流的两岸是平行的,由题意得:,,,
,
在和中,
,
≌,
,
的长为,
,
答:河宽为.
21.【答案】证明:,
,
在和中,
,
≌;
证明:过点作于,于,
≌,
,
在和中,
,
≌,
,
平分;
≌,
,
,
,
,
22.【答案】证明:延长,交于点,
,
,
点是的中点,
,
在与中,
,
,
平分,
,
,
,
,
,
.
23.【答案】解:;;
,,
理由:如图,
和均为等腰直角三角形,
,,,
在和中,
,
≌,
,
为等腰直角三角形,
,
点、、在同一直线上,
,
,,
,
,
,
解:和均为等边三角形,
,,.
,
在和中,
,
≌,
,
;
故答案为;
≌已证,
,
故答案为;
(满分:120分 时间100分钟)
一、选择题:本题共10小题,共30分。
1.在一些美术字中,有的汉字是轴对称图形.下面个汉字中,可以看作是轴对称图形的是( )
A. B. C. D.
2.用直角三角板,作的高,下列作法正确的是( )
A. B. C. D.
3.下列长度的三条线段能首尾相接构成三角形的是( )
A. ,, B. ,,
C. ,, D. ,,
4.正十边形的外角和的度数为( )
A. B. C. D.
5.点关于轴的对称的点的坐标是( )
A. , B. C. D.
6.如图,已知,补充下列哪一个条件,
仍不能判定和全等的是( )
A. B. C. D.
7.如图,中,,为中点,把纸片沿对折得到,如图,点和点分别为,上的动点,把纸片沿折叠,使得点落在的外部,如图所示.设,则下列等式成立的是( )
A. B. C. D.
8.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质( )
A. B.
C. D.
9.某班开展“用直尺和圆规作角平分线”的探究活动,各组展示作图痕迹如下,
其中射线为的平分线的有( )
A. 个 B. 个 C. 个 D. 个
10.如图,在平面直角坐标系中,对进行循环往复的轴对称变换,若原来点坐标是,则经过第5次变换后点的对应点的坐标为( )
A. B. C. D.
第II卷(非选择题)
二、填空题:本题共5小题,共15分。
11.如图,小林从点向西直走米后,向左转,再走米,如此重复,小林共走了米回到点,则为______.
12.如图,在中,,,的垂直平分线交于,交于,
若,则_____ _____.
13.如图,在平面直角坐标系中,为坐标原点在中,,若点的坐标为,则第二象限的点的坐标是______.
11题图 12题图 14题图
如图在中,,高,交于点若,,则 ______.
15.如图,在中,,平分,交于点,点、分别为、上的动点,若,的面积为,则的最小值为 .
14题图 15题图
三、解答题:本题共8小题,共75分。
16.分中,,平分交于点.
若,,求和的大小.
若,由的计算结果,你能发现与的数量关系吗?
写出这个关系式,并加以证明.
17.8分作图题:要求保留作图痕迹,不写作法
作中边上的垂直平分线,交于点,交于点;
连接,若,,求的周长.
18.9分如图,在中,,,平分交于点求证:.
19.分如图,在单位长度为的正方形网格中,已知的三个顶点都在格点上.
画出关于直线的轴对称图形;
求的面积.
20.10分某段河流的两岸是平行的,某数学兴趣小组在老师的带领下不用涉水过河就能测得河的宽度他们是这样做的:
在河流的岸边点处,选对岸正对的一棵树;
沿河岸直行处有一棵树,继续前行到达点处;
从点处沿河岸垂直的方向行走,当到达树正好被树遮挡住的点处时,停止行走;
测得的长为.
根据测量数据求河的宽度.
21.10分如图,,,,、交于点,连.
求证:≌;
求证:平分;
求的度数.用含的式子表示
22.10分如图,,平分,点为中点,求证:.
23.11分如图,和均为等边三角形,点,,在同一直线上,连接.
填空:的度数为 ;
线段,之间的数量关系为
如图,和均为等腰直角三角形,,点,,在同一直线上,为中边上的高,连接,请判断的度数及线段,,之间的数量关系,并说明理由.
参考答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
解:如图,
,为中点,
,,
,
如图,设 与交于点,
把纸片沿折叠,
,
在四边形中,,
,
,
,
,
,
由图可知,
.
8.【答案】
解:如图,由作图可知,.
在和中,,
≌,
故选:.
9.【答案】
10.【答案】
11.【答案】
解:设边数为,根据题意,
,
则.
故答案为:.
12.【答案】
解:如图,连接.
的垂直平分线交于,
,
,
.
又在中,,,
.
所以:
故答案是:.
13.【答案】
解:作轴于点,轴于点.
,,
,
,
,
在与中,
,
≌,
,
,,
,
答案为:.
14.【答案】
解:,,
,
,
,,,
,
在和中,
,
≌,
,
,
,
,答案为:.
15.【答案】
【解解:连接,过点作于点,如图:
,平分,
且平分,
是线段的垂直平分线,
,
,
根据“垂线段最短”得:,
即当点在线段上时,为最小,最小值为线段的长,
的面积为,,
,
,
的最小值为.
故答案为:.
16.【答案】解:,,
,
平分,
,
,
,
,
,
;
结论:.
理由:三角形的内角和等于,
,
平分,
,
,
,
,
.
17.【答案】解:如图,直线即为所求.
直线为线段的垂直平分线,
.
的周长为.
18.【答案】证明:,,
,
平分交于点,
,
,
,
19.【答案】
的面积为
20.【答案】解:河流的两岸是平行的,由题意得:,,,
,
在和中,
,
≌,
,
的长为,
,
答:河宽为.
21.【答案】证明:,
,
在和中,
,
≌;
证明:过点作于,于,
≌,
,
在和中,
,
≌,
,
平分;
≌,
,
,
,
,
22.【答案】证明:延长,交于点,
,
,
点是的中点,
,
在与中,
,
,
平分,
,
,
,
,
,
.
23.【答案】解:;;
,,
理由:如图,
和均为等腰直角三角形,
,,,
在和中,
,
≌,
,
为等腰直角三角形,
,
点、、在同一直线上,
,
,,
,
,
,
解:和均为等边三角形,
,,.
,
在和中,
,
≌,
,
;
故答案为;
≌已证,
,
故答案为;
同课章节目录
